Кривые второго порядка

O(0,0)

Фокусы гиперболы расположены в точках F1( c;0) , F2 (c;0) , где c половина расстояния между фокусами.

Точки A1( a;0) , A2 (a;0) называются вершинами гиперболы, точка

центром гиперболы. Расстояние между вершинами A1 и A2 , равное 2a , называется действительной осью гиперболы, а расстояние между точками B1(0; b) и B2 (0;b) , равное 2b , − ее мнимой осью.

Числа a , b и c связаны соотношением c2 a2 b2 . Прямоугольник, центр которого совпадает с точкой O(0;0) , а сто-

роны равны и параллельны осям гиперболы называется основным прямоугольником гиперболы. Диагонали основного прямоугольника гиперболы лежат на двух прямых, называемых асимптотами гипер-

болы; они определяются уравнениями y ba x.

При построении гиперболы целесообразно сначала построить основной прямоугольник гиперболы, провести прямые, проходящие через противоположные вершины этого прямоугольника, − асимптоты гиперболы и отметить вершины A1 и A2 гиперболы.

Форма гиперболы зависит от угла наклона асимптоты к действи-

тельной оси, т. е. от величины отношения ba : чем эта величина мень-

ше, тем меньше угол между асимптотами, в котором заключена ги-

пербола, и тем более сжата сама гипербола; чем больше величина ba ,

тем круче располагаются ветви гиперболы.

Но, так же как и для эллипса, в качестве характеристики формы ги-

перболы пользуются не величиной отношения ba , а величиной ac ,

называемой эксцентриситетом гиперболы.

Эксцентриситетом 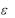гиперболы называется отношение расстояния между фокусами 2c к величине действительной оси 2a :

ac ( 1 , т. к. c a ).

Расстояния r1 и r2 от произвольной точки M (x ; y) гиперболы до ее фокусов называются фокальными радиусами этой точки.

11

Фокальные радиусы определяются формулами:
для точек правой ветви гиперболы: r1			a	x , r2	a	x ;
для точек левой ветви: r1	a	x , r2	a	x .

Директрисами гиперболы называются прямые параллельные мни-

мой оси гиперболы и отстоящие от нее на расстоянии, равном a ;

уравнения директрис: x	a	и x	a	.

Замечания.

1) если a b , то уравнение (3) определяет равностороннюю (рав-

нобочную) гиперболу x2 y2 a2 ;

2) если a b , то уравнение гиперболы имеет вид:

y2		x2	1	,	(4)
b2		a2

действительная ось которой 2b расположена на оси Oy , а мнимая ось 2a на оси Ox . Фокусы такой гиперболы находятся в точках F1(0; c)

и F (0;c) , где c2		a2		b2 . В этом случае: асимптоты определяются
2
уравнениями y		b	x,		c	, уравнения директрис	y	b	. Гипер-
		a			b

бола (4) называется сопряженной гиперболе (3); 3) уравнение гиперболы с осями, параллельными координатным,

имеет вид:
	(x x )2		( y y	0	)2
0						1,		(5)
	a2		b2
где (x0; y0 ) координаты центра гиперболы.
						x2		y2
Пример 3.1. Дано уравнение гиперболы									1 . Определить:
						64		36

1)действительную и мнимую оси;

2)координаты фокусов и расстояние между ними;

3)эксцентриситет гиперболы;

4)уравнения директрис и асимптот.

Решение. 1) Из канонического уравнения гиперболы: a2	64 , a 8
и b2 36 , b 6 . Действительная ось 2a 16 , мнимая ось 2b	12 .

12

2) Из соотношения c2

a2

b2 , находим c

64 36

10 .

Следовательно,

F1( 10;0) и

F2 (10;0) , а расстояние между фокуса-

ми составляет 2c

20 .

3)

c

10

5

1,25 .

a

8

4

4) Уравнения директрис: x

a

8

32

6,4 и x

a

6,4 .

5

5

4

Асимптоты гиперболы определяются уравнениями:

y

b

x

6

x

0,75x и y

0,75 x.

a

8

Ответ: 1) 2a 16 ,

2b 12 ;

2) F1(

10;0) , F2 (10;0) ,

2c 20 ;

3)

1,25 ; 4) x

6,4 , x

6,4 ;

y

0,75x ,

y

0,75 x.

Пример 3.2. Составить уравнение гиперболы, если ее фокусы лежат на оси Oy и расстояние между ними равно 10, а длина действи-

тельной оси равна 8.

Решение. Искомое уравнение гиперболы имеет вид

y2

x2

1.

b2

a2

Согласно условию 2c

10 , c 5 ,

2b

8 , b

4 .

Из

соотношения

c2 a2 b2 найдем мнимую полуось

a :

25

a2

16 ,

a2

9 , a 3 .

y2

x2

Получаем

1

уравнение гиперболы.

16

9

y2

x2

Ответ:

1.

16

9

4. Парабола

Параболой называется множество всех точек плоскости, каждая из которых равноудалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой (рис.5).

Расстояние от фокуса F до директрисы называется параметром

параболы и обозначается через p ( p	0) .
Каноническое уравнение параболы:	y2 2 px .

13

	Фокус F имеет координаты					p	;0	, а уравнение директрисы имеет
					2
		p			y
	вид x		.
		2
											M x ; y
				p
									r
		2
					O			F		p	x
											;0
									2

Рис. 5 Прямая, проходящая через фокус параболы перпендикулярно ее

директрисе, называется осью, а точка пересечения параболы с ее осью

вершиной параболы.

Точка O (0;0) − вершина параболы, Ox − ось симметрии параболы. Длина r отрезка FM − фокальный радиус точки M (x ; y) :

r x 2p .

Замечания.

1) Парабола, симметричная относительно оси Oy и проходящая через начало координат (рис. 6), имеет уравнение x2 2 py .

y

		M (x; y)
	r
F
O					x
	y		p
		2
Рис. 6

14

Фокусом параболы является точка F 0; 2p . Уравнение директри-

	сы этой параболы y	p	, а фокальный радиус точки M (x ; y) :
		2

ry 2p .

2)Уравнения y2 2 px (рис. 7), x2 2 py (рис. 8) также определяют параболы.

y

F	p	;0	O				x
	2						p
					x
							2
			Рис. 7
						y			p
							2
			O								x
			F 0;		p
				2
			Рис. 8

15

3) Уравнения

( y

y

0

)2

2 p (x

x ) и (x

x )2

2 p ( y

y

0

)

задают

0

0

параболы, но с вершинами в точке (x0 ; y0 ).

При

p

0 первая из этих парабол направлена в сторону отрица-

тельной оси Ox , вторая − в сторону отрицательной оси Oy.

Пример 4.1. Написать уравнение параболы, проходящей через точ-

ки (0;0)

и (2;3) , если парабола симметрична относительно оси Ox .

Решение. Так как парабола симметрична относительно оси Ox и

проходит

через

начало координат, то

ее

уравнение

имеет

вид

y2

2 px . Учитывая, что парабола проходит через точку (2;3) , имеем

32

2 p

2 , откуда

p

9

. Следовательно,

y2

9x

− искомое уравне-

2

4

ние.

Ответ:

y2

9x

.

2

Пример 4.2. Составить уравнение линии, каждая точка которой

равноудалена от точки F (0;

4) и прямой y

2

0.

Решение. Пусть M (x; y)

− произвольная точка линии,

N (x; 2) −

основание перпендикуляра, опущенного из

точки

M

на

прямую

y

2 0 . По условию задачи MF

MN или

(x

x )2

( y

M

y

F

)2

(x

x

N

)2

( y

M

y

N

)2 .

M

F

M

Подставляя координаты точек

(x

0)2

( y

( 4))2

(x

x)2

( y

(

2))2

и возведя в квадрат,

после преобразований получаем: x2

4 y

12

или x2

4 ( y

3) . Получили уравнение параболы.

Ответ:

x2

4

( y

3).

16

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Студент выполняет индивидуальные задания по варианту, номер которого соответствует номеру его фамилии в журнале посещаемости занятий. Работа должна быть выполнена в отдельной тетради. Условие каждого задания следует записывать полностью, а решения подробно. Необходимые чертежи должны выполняться четко. Студент защищает свою работу у преподавателя.

Задание 1. Установить, какую линию определяют следующие уравнения:

1.1.

x2

y2

8x

4 y

5

0 .

1.2. x2

y2 6x

6 y

22

0 .

1.3.

2x2

2 y2

8x

5 y

4

0 .

1.4. x2

y2

2x

4 y

4

0 .

1.5. 3x2

3y2

6x

18 y

48

0 .

1.6. x2

y2

2x

4 y

6

0 .

1.7. 3x2

3y2

6x

18 y

30

0 .

1.8. x2

y2

2x

4 y

5

0 .

1.9. 3x2

3y2

6x

18 y

50

0 .

1.10. x2

y2

4x

8 y

16

0 .

1.11. x2

y2

2x

6 y

6

0 .

1.12. 3x2

3y2

4x

9 y

4

0 .

1.13. x2

y2

4x

14 y

54

0 .

1.14. 2x2

2 y2

8x

5 y

4

0 .

1.15. x2

y2

2x

4 y

4

0 .

1.16. x2

y2

6x

10 y

15

0 .

1.17. x2

y2

4x

6 y

3

0 .

1.18. 4x2

4 y2

8x

12 y

13

0 .

1.19. x2

y2

4x

8 y

16

0 .

1.20. x2

y2

10 x 6 y 16

0 .

1.21. x2

y2

8x

12 y

14

0 .

1.22. 9x2

9 y2

42x

54 y

95

0 .

1.23. x2

y2

6x

10 y

30

0 .

1.24. x2

y2

10 x

4 y

29

0 .

1.25. 3x2

3y2

6x

4 y

2

0 .

1.26. x2

y2

4x

8 y

16

0 .

1.27. x2

y2

x

6 y 13

0 .

1.28. 3x2

3y2

6x

4 y

2

0 .

1.29. x2

y2

6x

8 y

16

0 .

1.30. x2

y2

10 x

4 y

13

0 .

1.31. x2

y2

8x

2 y

16

0 .

1.32. x2

y2

2x

4 y

4

0 .

1.33. x2

y2

10 x

6 y

25

0 .

1.34. x2

y2

8x

4 y

16

0 .

1.35. x2

y2

8x

4 y

5

0 .

1.36. x2

y2

6x

4 y

23

0 .

17

1.37. x2		y2 5x 7 y			5	0 .			1.38. x2		y2 4x 2 y 1				0 .
1.39. 2x2		2 y2		4x	8 y	6	0 .		1.40. x2		y2	8x 6 y 11 0 .
	Задание 2. Определить тип кривой второго порядка, заданной
уравнением Ax2				2Bxy		Cy 2	2Dx		2Ey		F	0 . Построить кривую.
	Вариант			A		2B			C		2D		2E		F
	1			1		0			1		−8		2		−11
	2			1		0		−4			−6		−8		−7
	3			16		0		−9			−64		−54		−161
	4			5		0		−9			−30		18		−9
	5			16		0		−25			32		−100		84
	6			5		0			9		30		−18		9
	7			4		0			3		−8		12		−32
	8			1		0			5		−1		10		−3
	9			9		0		−16			−36		−32		−124
	10			5		0			9		−30		18		9
	11			16		0		−9			−64		−18		199
	12			4		0			3		−8		12		−32
	13			9		0		−16			90		32		−367
	14			16		0		25			32		−100		−284
	15			5		0			2		−50		−8		−27
	16			3		0		−1			−6		4		−7
	17			4		0		25			4		−10		−8
	18			3		0		−4			−12		−8		20
	19			2		0		−4			5		−6		−1
	20			3		0			4		12		−4		1
	21			2		0			3		−4		6		−7
	22			1		0			4		2		16		−5
	23			9		0			4		36		−40		100
	24			9		0		−4			−36		−16		−16
	25			3		0		−9			−30		30		15
	26			5		0			3		40		−6		98
	27			16		0		25			32		−100		−284
	28			2		0			1		−8		−6		1

18

Вариант	A	2B	C	2D	2E	F
29	1	0	−4	−8	0	0
30	5	0	9	−30	18	9
31	4	0	−1	8	−8	5
32	1	0	25	−2	50	−20
33	1	0	−9	2	−36	−20
34	−1	0	9	−8	18	4
35	4	0	9	−2	9	−10
36	4	0	−1	4	−2	6
37	1	0	5	−1	10	−3
38	−4	0	9	8	−18	41
39	5	0	10	−10	10	−1
40	1	0	−4	4	−8	11

Задание 3. Составить каноническое уравнение параболы, если известно, что:

3.1. парабола симметрична относительно оси Ox и проходит через точку M (4; 2) ;

3.2. F (2;0) и уравнение директрисы х 4 0 ;

3.3.парабола симметрична относительно прямой х 1 0 и проходит через точку M (2;0) , а ее вершина находится в точке A(1; 2) ;

3.4.парабола симметрична относительно оси Oy и проходит через точку M (1; 2) ;

3.5. F (2;6) и уравнение директрисы х 4 0 ;

3.6.парабола симметрична относительно оси Ox и фокус находится в точке ( 3;0) ;

3.7.парабола симметрична относительно оси Ox , фокус находится

вточке ( 2;0) , а вершина в начале координат;

3.8.уравнение директрисы x 3 0 ;

3.9.парабола симметрична относительно оси Ox и проходит через точку M ( 3;6) и начало координат;

3.10. F (2;6) и уравнение директрисы y 10 0 ;

3.11. парабола симметрична относительно оси Oy и фокус находится в точке (0;5) ;

3.12. F (3; 4) и уравнение директрисы y 0 ;

19

3.13.парабола симметрична относительно оси Ox и проходит через точку M (2; 3) ;

3.14.парабола имеет фокус F (0;2) и вершину в точке O(0;0) ;

3.15.парабола симметрична относительно оси Oх и проходит через точки O(0;0) и M (1; 4) ;

3.16.фокус находится в точке (5;0) , и директриса будет осью ор-

динат и ось симметрии − осью абсцисс;

3.17. парабола симметрична относительно оси Oy и проходит через точки O(0;0) и M (6; 2) ;

3.18. уравнение директрисы 2 y 7 0 , вершина в точке (0;0) ;

3.19.парабола симметрична относительно оси Oy и проходит че-

рез точки O(0;0) и M (6;3) ;

3.20.фокус находится в точке (0;5) , и директриса служит осью

абсцисс и ось симметрии − осью ординат;

3.21.парабола симметрична относительно оси Oy и проходит через точки O(0;0) и M (6; 2) ;

3.22.парабола имеет фокус F (0;2) и вершину в точке O(0;0) ;

3.23. парабола симметрична относительно прямой y 2 0 и проходит через точку M (2;0) , а ее вершина находится в точке A(1; 2) ;

3.24.парабола симметрична относительно оси Oy и проходит через точки O(0;0) и M ( 2;4) ;

3.25.парабола симметрична относительно оси Ox и проходит через точку M (9;6) ;

3.26.уравнение директрисы y 1 ;

3.27.парабола симметрична относительно оси Oy и проходит через точку M (1;1) ;

3.28.уравнение директрисы y 2 0 ;

3.29.парабола симметрична относительно оси Oх и проходит через точки O(0;0) и M ( 1;2) ;

3.30.уравнение директрисы x 14 ;

3.31.парабола симметрична относительно оси Oy и проходит че-

рез точки O(0;0) и M (2;4) ;

20