4. Блок контроля освоения дисциплины

4.1. Методические указания к выполнению контрольных работ и задания на контрольные работы

Во второмсеместре студенты выполняют контрольные работы № 3 и № 4 . Прежде чем выполнять контрольные работы, следует изучить теоретический

материал по указанной литературе, разобрать решения типовых задач, приведенных в данном комплексе, выработать навыки решения примеров и задач по соответствующей теме, проверив себя по тренировочным тестам, приведенным в 4.3. При выполнении контрольных работ необходимо придерживаться указанных ниже правил:

1. Контрольная работа должна быть выполнена студентом в отдельной ученической тетради в клетку, с полями не менее 3 см для замечаний преподавателя или предоставлена в электронном виде на учебном сайте СЗТУ.

2. На титульном листе указывается фамилия, имя, отчество студента,

шифр (номер студенческого билета), курс, факультет и специальность, по

которой студент обучается, номер контрольной работы, год издания

методических указаний, из которых взято контрольное задание.

3.Условия задачи приводятся полностью, без сокращения слов, после чего приводится подробное решение со ссылками на использованные при решении определения, теоремы, формулы; в конце решения записывается ответ; чертежи можно выполнять аккуратно от руки.

4.В работу должны быть включены все задачи, указанные в задании, строго по варианту. Контрольные задания, содержащие не все задачи, а также задачи не своего варианта, не зачитываются.

5.Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку.

6.Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления.

4.1.1.Методические указания по выполнению контрольной работы N 3

Применение правила Лопиталя к нахождению

предела функции

ряде

00 ,

	При отыскании предела lim (x) подстановка предельного значения							x a в
					x a
			случаев	приводит	к	неопределенным	выражениям	типа:
		,	0 , , 00 , 0 ,1 .			Тогда вычисление заданного		предела

называют раскрытием неопределенности соответствующего типа. Обычно при этом используют правило Лопиталя.

Раскрытие неопределенностей типа 00 и

Непосредственно применять правило Лопиталя можно только для раскрытия неопределенностей типа 00 или . Согласно этому правилу, предел отношения

двух бесконечно малых (или двух бесконечно больших) существует и равен пределу отношения их производных:

	lim	f (x)	lim	f (x)	,
		g(x)		g (x)
	x a		x a

если выполнены условия:

1) функции f (x) , g(x) дифференцируемы в некоторой окрестности точки x a и g (x) 0 в этой окрестности (кроме, может быть самой точки a );

2)

lim f x lim g x 0 (или lim

f x lim g x );

x a

x a

f (x)

x a

x a

3)

существует lim

(конечный

или

бесконечный),

при этом a

g (x)

x a

может быть как числом, так и одним из символов: , , .

Пример 1. Найти

lim

1 2 cos x

.

sin 3x

x

3

Решение. Поскольку

lim 1 2 cos x 1 2 cos

x

3

3

1

1 2

0,

2

0 и lim sin 3x sin 3

3

sin 0

x

3

то имеем неопределенность

типа 0 . Функции

1 2 cos x

и

sin 3x

0

дифференцируемы на всей числовой оси. Найдем предел отношения их производных:

0 2 sin x

2sin x

lim

1 2 cos x

lim

lim

3cos 3x

x

3

sin 3x

x

3 cos 3x 3x

x

3

2sin 3

2 3 2

3

.

3cos 0

3

3 1

Так как этот предел существует, то, согласно правилу Лопиталя:

lim

1 2 cos x

lim

1 2 cos x

3

.

x

3 sin 3x

x

3

3

sin 3x

Замечание. Если

предел отношения производных

lim

f (x)

вновь

g (x)

x a

представляет собой неопределенность типа 00 или , то правило Лопиталя применяется еще раз.

Раскрытие неопределенностей типа 0 и
Неопределенность типа 0	или следует вначале	путем
тождественных преобразований привести к неопределенностям типа 0		или		,
	0

для раскрытия которых можно непосредственно применить правило Лопиталя.

Пример 2. Найти

lim

cos x ln 2x .

x o

2

Решение.

При

x

2 o

аргумент

логарифмической

функции

2x 0 o. Так

cos x 0

lim ln 2x , то

как

lim

и

x o

x o

2

0 . Обычно

2

возникает неопределенность

типа

в таких случаях один из

сомножителей записывают в знаменатель данного выражения:

lim

cos x ln 2x

lim

ln 2x

.

1

1

cos x

x 2

o

x

2 o

Получена

неопределенность

типа

,

к

которой применимо

правило

Лопиталя:

1

2

ln 2x

ln

2x

lim

lim

lim

2x

1

2

cos x

o cos x

sin x

x 2 o

x

2 o

cos x 1

x 2

2

lim

cos2 x

lim

1

2

lim

cos2 x

x o

2x x o sin x

x

o 2x

2

2

2

0

(поскольку

lim sin x 1). Здесь имеет место неопределенность типа

, для

0

x 2 o

раскрытия которой снова применяем правило Лопиталя:

2 lim			cos2 x	2	lim					cos2 x			2		lim			2 cos x sin x
																		2
x		o 2x		x				o 2x							x		o
	2						2				2 0 1					2
						2								0.
												2
					1					1
Пример 3. Найти lim												.
									e x
				x 0 x							1

Решение. Выражение в скобках, представляющее собой неопределенность типа , приводим к общему знаменателю:

lim		1		1		lim	e x 1 x	.
							x e x 1
x 0 x				e x 1		x 0

Полученную неопределенность типа 00 раскроем по правилу Лопиталя (в ходе вычислений это правило применено дважды):

e x

1 x

e x 0

1

lim

lim

e x 1 x

lim

x e

x

1

x e x 1

1 e

x

1 xe

x

x 0

x 0

x 0

e x

e x

1

1

lim

e x 1

lim

lim

lim

.

x

x

x

x

x 0 e

0 e

xe

x 0 e

(2

x)

x 0 2 x 2

x 0 e x 1 xex

Раскрытие неопределенностей типа 1 , 00 , 0

Прираскрытииуказанныхнеопределенностейиспользуются:

а) основное логарифмическое тождество aloga b b (в частности,

eln b b );

б) непрерывность показательной функции, в силу чего:
		lim f x	.
		lim e f x ex a
		x a
Пример 4. Найти lim		2 ex ctg3x .
x 0 o
Решение. Поскольку	lim 2 e x 2 1 1,		lim ctg3x , имеем
x 0 o			x 0 o

неопределенность типа 1 . Найдем вначале предел логарифма заданной функции:

lim

ex

ctg3x

ctg3x ln 2 ex .

Здесь

возникла

ln 2

lim

x 0 o

x 0 o

1

неопределенность типа

0 . Если учесть,

что

ctg3x

,

то перейдем к

0

tg3x

неопределенности типа

, которую можно раскрыть по правилу Лопиталя:

0

ln 2 ex

ln

x

lim ctg3x ln 2 ex

lim

lim

2 e

x 0 o

e x

x 0 o

tg3x

x 0 o

tg3x

1

e x cos2 3x

1 12

lim

2 e x

1 lim

1

1 .

3

2 1

x 0 o

1

3

3 x 0 o

2 e x

3

cos2 3x

Теперь используем основное логарифмическое тождество и свойство

непрерывности показательной функции:

ctg3x

x

ctg3x

lim

ln

2 ex

1

1

lim

2 ex ctg3x

lim

eln 2 e

ex 0 o

e

3

.

x 0 o

x 0 o

3 e

Таким образом, для вычисления lim u(x)v( x)

в случае неопределенностей

x a

1 ,

00 ,

0 применяем правило: lim uv

eq ,

где

x a

q lim v ln u .

x a

Применение производной к исследованию функции. Построение графиков функций

Промежутки монотонности и точки экстремума функции

Чтобы определить промежутки возрастания и убывания функции y x , а также ее точки экстремума, надо вначале найти первую производную y (x) заданной функции. Затем следует определить промежутки, на которых эта производная сохраняет свой знак: там, где y (x) 0, функция y x возрастает; если же y (x) 0, то на этом промежутке функция y x убывает.

Чтобы найти точки экстремума (максимума или минимума) функции y x , прежде всего определяют критические точки функции y x , то есть

точки, входящие в множество определения функции, в которых выполняется необходимое условие экстремума: либо y (x) 0, либо y (x) , либо

y (x) не существует. Затем каждую из найденных критических точек

проверяют на наличие экстремума с помощью одного из достаточных признаков существования экстремума (по первой или второй производной).

Пример 5. Найти промежутки монотонности и точки экстремума

функции y		x4
				.
	x	3
			1
Решение. Прежде всего отметим, что данная функция определена на
всей числовой оси, кроме точки x 1. Продифференцируем эту функцию
				y			4x3 x3 1 x4 3x2			x3 x3 4
								x3 1 2		x3 1 2 .
Очевидно,			что точка					x0 1 не является		критической, поскольку не

принадлежит множеству определения функции. Имеем две критические точки,

в которых y 0 : это x1 0

и

x2 3 4

1,58.Чтобы найти промежутки

возрастания

функции

y(x) , надо решить неравенство

или

y

(x) 0,

x3 x3 4 0.

Оно

выполняется

при

x ;0 3

4;

-

это

x3 1 2

промежутки

возрастания

функции.

Соответственно,

при

y (x) 0

x 0;1 1;

3 4

- промежутки убывания данной функции.

В критических

точках

x 0;

x

3 4

проверим

выполнение

1

2

достаточного

условия

существования

экстремума

с использованием

первой

производной. При переходе через точку x 0 первая производная			y	меняет
знак с (+)	на (-), значит, x 0	- точка максимума. Аналогично,		точка
x2 3 4	- точка минимума, потому что при переходе через		нее первая
производная y меняет знак с (-) на (+).
Найдем экстремальные значения функции:
	max y(x) y(0) 0;	min y(x) y 3 4 34 3 4 2,1.

Выпуклость и вогнутость графика функции. Точки перегиба

Промежутки выпуклости и вогнутости графика функции, а также точки перегиба определяются с помощью второй производной y . На промежутках

выпуклости y 0 , на промежутках вогнутости y 0 .

Чтобы найти точки перегиба, исследуют точки, в которых либо y 0 , либо y , либо y не существует (причем в последних двух случаях y в

соответствующих точках определена). Точками перегиба являются те из найденных точек, при переходе через которые y изменяет свой знак.

Пример 6. Найти промежутки выпуклости и вогнутости, а также точки

перегиба функции y												x4						.
										x3				1															x6 4x3
Решение. Знаяпервуюпроизводную y
																											x3							1 2		, найдемвторую
																											2
	x 4x
	6					3								6x		5		12x			2		x	3	1						x	6		4x	3		2 x		3	1 3x			2			6x	2		x	3	2
	y
				1		2																				x			1				4													x			1			3
	x		3																									3																				3
																									.
Поскольку сама функция y в точке x0 1 не определена, то исследуем только
точки,	в которых				y 0 .									Точка						x3 0 не является точкой перегиба,																									так как при
прохождении			через				нее							вторая						производная											сохраняет							свой			знак				(-). Точка
x4 3 2 - это точка перегиба,																			поскольку при переходе через нее																							y меняет свой
знак с (+) на (-). Промежутки вогнутости графика данной функции:																																										; 3						2			и
															3
1; , на промежутке																				график функции выпуклый. Значение функции в
точке перегиба:					y 3				2									2 3		2 0,83.
																		3

Асимптоты графика функции

а) Прямая x a является вертикальной асимптотой графика функции		y(x) ,
если хотя бы один из односторонних пределов: lim	y(x) или lim	y(x)
x a o	x a o

обращается в бесконечность. Поэтому для отыскания вертикальных асимптот графика функции надо найти точки бесконечного разрыва данной функции, которые относятсяк точкам разрываII-го рода.

Пример 7. Найти вертикальные асимптоты графика функции y								x4
										.
								x3
									1
Решение. Как отмечалось, данная функция не определена в точке									x0 1.
При этом	x4				x4
lim			;	lim			.
x 1 o x3		1		x 1 o x3		1

Поэтому прямая x 1 является вертикальной асимптотой графика заданной функции.

б) График функции y(x) имеет наклонную асимптоту y kx b при x (x ) , если существуют конечные пределы:

k lim	y(x)	; b	lim y(x) kx .
x	x		x
( x )			(x )

Если хотя бы один из этих пределов несуществуетилибесконечен, тографик функциинеимеетнаклоннойасимптоты при x (x ) . (Если асимптота

задана уравнением y b, то ее называют горизонтальной).

Пример 8.

Найти наклонные асимптоты графика функции y

x4

.

x3

1

Решение.

Найдем значения k и b для данной функции при x .

k

lim

y(x)

lim

x3

lim

1

1.

x

1

x

x x3 1

x

1

x3

b lim y(x) 1x

x4

x4

x4 x

lim

x

lim

3

3

x

1

x

x

1

x x

lim

x

lim

1

0.

1

1

x x3

x

2

1

x

x

2

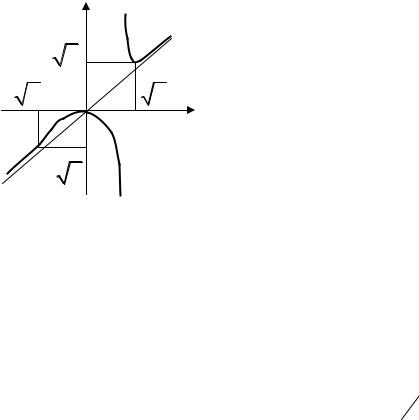
Аналогично находим, что при x по-прежнему k 1; b 0 . Таким

образом, график функции y	x4
			имеет одну и ту же наклонную асимптоту
	x3
		1

при x и x ; это прямая y x .

Общий план исследования функции

Чтобы составить достаточно полное представление о характере поведения функции и построить ее график, удобно проводить ее исследование по следующему плану:

1.Установить множество определения функции; при наличии точек разрыва найти в них односторонние пределы данной функции;

2.а) Найтиточкипересеченияграфикафункциисосямикоординат,

б) Отметить особенности графика заданной функции, не связанные с производными, например, симметрию, периодичность.

3.Установить промежутки возрастания и убывания функции, найти ее экстремумы.

4.Установить промежутки выпуклости и вогнутости график функции, найти точки перегиба.

y

5 Найти асимптоты графика функции.

4

Пример 9. Исследовать функцию y

x

и

4 3

4

y x

x3 1

3

сделать схематический чертеж ее графика.

3

O

3

4

x

Решение.

Как отмечалось

в примере

5,

2

множество определения данной

функции -

вся

x 1

числовая

ось

Ox ,

исключая

точку

2 3

2

x 1:

X ;1 1; .

График функции

пересекается с осями координат в единственной

3

точке 0(0,0). Функция не является ни четной, ни

( x)4

x4

нечетной,

поскольку

y( x)

y(x)

и

y( x) y(x) ,

поэтому

график

( x)3 1

x3

1

функции не обладает свойствами симметрии. Дальнейшее исследование этой функции фактически уже проведено в примерах 5-8. По данным, полученным в этих примерах, сделан схематический чертеж графика заданной функции,

который представлен на рис. 1.	Рис. 1	1x и сделать схематический
Пример 10. Исследовать функцию y xe

чертеж ее графика.

Ox ,	Решение. 1. Множество определения данной функции - вся числовая ось
	кроме	точки	x 0 :		X ( ;0) (0; ) .			Найдем	односторонние
пределы функции			при	x 0 .		Предел	слева	lim xe 1x	0, так как
		и lim e 1x						x 0 o
lim	x 0				lim	e y 0.	При вычислении		предела справа
x 0 o		x 0 o			y

возникает неопределенность вида 0 ; приводим ее к неопределенности вида

, к которой применяем правило Лопиталя:

1

1

lim xe1 x lim

e

x

e

x

lim

1x

x 0

o

x 0 o

x

0 o

1x

lim

e1 x 1x2

lim e1 x

.

x 0 o

1x2

x 0 o

2. а) Точки пересечения графика функции с осью Ox определяются из

условия y 0. В данном случае уравнение xe 1x

0 не имеет решений, так как

x 0 не входит в множество определения функции. Точки пересечения графика функции с осью Oy можно найти, положив x 0. Для заданной функции это

значение не входит во множество ее определения. Следовательно, график исследуемой функции не имеет точек пересечения с осями координат.

б) Поскольку y( x) xe x y(x) и y( x) y(x) , то функция не является ни четной, ни нечетной.

3.

Находим

1x

1

1

1

1

e

y xe

x

e

x xe

x

(x 1).

x2

x

Производная у' существует и конечна на всем множестве определения заданной функции X ( ;0) (0; ) . Поскольку точка разрыва первой

производной х = 0 не принадлежит множеству определения функции, то все

критические точки функции y x находим из условия:		y 0, или
e 1x	(x 1) 0 . Отсюда получаем x 1.
x

Функция

y x

возрастает,

если

y ' x 0,

то есть при

x 0 и

1 x .

y x

если y ' 0,

0 x 1.

Функция

убывает,

в данном случае при

Таким образом, при переходе через точку

x 1 первая производная меняет

знак с (-) на (+), то есть x 1 - точка минимума; y(1)

min y(x) e.

4. Находим

1x

y

1

1

1

1

1

1

1

e

e

x 1

e

x

1

e

x

.

x

2

x

2

3

x

x

x

Вторая производная существует и конечна во всех точках множества определения данной функции. Тогда все точки перегиба находим из условия:

1

y 0 , то есть e 3x 0 . Поскольку это уравнение не имеет решения, то x

точек перегиба нет. График функции - выпуклый, если		y 0 ;	в данном
случае при x 0. График функции вогнутый при x 0, так как там y 0 .
5. Как было установлено в пункте 1, в	точке	x 0	функция
y xe 1x имеет бесконечный разрыв, поэтому	прямая	x 0	является

вертикальной асимптотой ее графика. Для определения наклонных асимптот найдем:

k

lim

y(x)

lim

e 1x

e0

1,

x

x

x

1 x 1

b lim

y(x) kx

lim

1

1

x

lim

e

xe

x x lim

x e

1

1

x

x

x

x

x

1

1

x

e

x

1

e

1

1 x

lim

lim

x2

lim

e

e

0

1.

1x

1x2

x

x

x

Значит,

прямая

y x 1

является

y

y x 1

наклонной

асимптотой

графика

функции

при

x

и x

.

Схематический

чертеж

e

графика функции приведен на рис. 2.

Пример

11.

Исследовать

функцию

1

x

y 3 x2 1 2

и сделать схематический чертеж

1

O

графика.

Рис. 2

Решение:

1. Данная функция определена

на всей числовой

оси 0x : X ( ; ).

2. Точки пересечения графика функции с осью Ox определяются из

условия

y 0, откуда

x 1, а с осью Oy

-

из условия x 0, при этом

y 0 1.

Данная

функция

-

четная,

поскольку

y( x) 3

x 2

1 2

3

x2

1 2 y(x) , значит,

ее график симметричен

относительно оси Oy .

2

2

1

4x

3. y x2

1

3

3

x2

1

3

2x

. Первая

производная

33

x2

x 1,

1

обращается в бесконечность в точках

x 1, в то время, как сама

функция

y 3 x2 1 2

в

этих

точках

определена. Значит,

эти точки -

критические для данной функции. Еще одна критическая точка определяется

из условия		y 0; это x 0.		Функция убывает,		если	y 0 ,	то есть при
x 1 и 0 x 1. Функция возрастает						при	y 0 ,	то есть при
1 x 0		и при	x 1. Таким образом,		x 0 - точка		максимума, x 1 и
x 1	-	точки	минимума	данной	функции;		y(0) max y(x) 1;
y( 1)	y(1) min y(x) 0. В			точках x 1 и x 1 данная функция имеет

так называемый "острый" экстремум: касательная к графику функции в каждой из этих точек параллельна оси Oy .

4

1

4

x2 3

4.

y

x x2

1

3

.

Вторая

производная

3

9

3 x2 1 4

обращается

в бесконечность

при

x 1, но эти

точки не

принадлежат

множеству определения

и, следовательно, не являются критическими

y (x)

точками для второй производной. Значит, критические точки для нее

определяем	из	условия y 0 , откуда			x 3 .	Так как y 0 при
x	3 и		3 x ,	то график y(x) в этих интервалах вогнутый,
а в интервалах			3 x 1;	1 x 1;	1 x	3 - график выпуклый,

так как там y 0 . Значения функции в точках перегиба

y 3 y 3 3 4.

5. Поскольку функция определена на всей числовой оси Ox, то вертикальных асимптот у ее графика нет. Проверим наличие наклонных асимптот:

y

k

lim

3 x2 1 2

lim

3

x2 1 2

.

x

3 4

x

x

x3

x

Таким образом, наклонные асимптоты

3 1 O 1

также отсутствуют. На рис. 3 схематически

3

изображен график функции y 3

x2

1 2 .

Рис. 3

Неопределенный интеграл

Интегрирование - нахождение функции по ее дифференциалу - это

математическая операция, обратная дифференцированию функции.

В то время, когда дифференцирование функции проводится на основании

общего правила, вытекающего из определения производной, для интегрирования

функции нельзя указать такие общие правила. Техника интегрирования основана

на применении основных свойств неопределенного интеграла и таблицы

основных интегралов.

Основные свойства неопределенного интеграла

1.

f (x); d

f (x)dx f (x)dx;

f (x)dx

2. C1 f1 (x) C2 f2 (x) dx C1 f1 (x)dx C2 f2 (x)dx;

f (x)dx

F (x) C, то

f

x

x

F

(x)

C;

3.

Если

d

(инвариантность формул интегрирования) 4. dF (x) F (x) C .

Таблица основных интегралов

1 . 0 d x C ;

2 . x m d x

x m 1

C ,

m 1;

m 1

d x

4 . a x d x

a x

C , a 0 , a 1

3 .

ln | x

| C ;

ln a

x

в частн о сти , e x d x e x

C ;

5 . co s xd x sin x C ;

6 . sin x d x co s x C ;

7 .

d x

tg x C ;

8 .

d x

ctg x C ;

2

x

2

x

co s

sin

9 .

d x

arcsin x

C ,

1 0 .

d x

arctg x C ,

1 x 2

1 x 2

arcctg x C ;

arcco s x

C ;

arcsin

x

C ,

1

arctg

x

C ,

d x

| a

|

d x

a

a

1 1 .

1 2 .

x

a 2 x 2

x

a

2

x

2

C ;

1

C ;

arcco s

|

a

|

a

arcctg

a

1 3 .

d x

x 2 a 2

C ;

1 4 .

d x

1

x a

C .

ln

x

ln

x 2 a 2

x 2 a 2

2 a

x a

Основная трудность при интегрировании состоит в приведении подынтегрального выражения к виду, позволяющему использовать таблицу интегралов. Для некоторых видов подынтегральных функций можно указать ряд приемов, позволяющих это сделать.

Метод замены переменной интегрирования (метод подстановки)

Суть этого метода состоит в преобразовании данного подынтегрального выражения кподынтегральному выражениюужеизвестнойформулы интегрирования

с помощью замены переменной по формуле x (t) или t (x) (причем функции (t) или (x) должны иметь обратную функцию и быть непрерывно

	дифференцируемыми).
	Пример 12. Найти I	ex 3e2x	1	e2x cos 5x	dx.
		1	e2x

Решение. Разделив почленно числитель подынтегральной дроби на выражение, стоящее в знаменателе, и, применив свойство 2, получим сумму трех интегралов

I

e x

3

e2x dx

cos 5xdx.

1

e2x

1 e2x

переменную t ex , тогда

В первом из

них

введем

новую

dt ex dx exdx

и

exdx

dt

arcsin t C arcsin ex C

1 e2x

1 t2

(использована формула 9 из таблицы интегралов). Вычисляя второй интеграл, введем переменную z 1 e2x , при этом dz 1 e2x dx 2e2xdx, тогда

e2 xdx

1

dz

1

z

1

2 dz

1 z 12

C

z C 1 e

2 x

C.

1 e2 x

2

z

2

2

1

2

m 1 ).

(применена формула

2

из

таблицы

интегралов,

причем

При

2

t , а

нахождении последнего интеграла можно не вводить новую переменную

использовать прием, называемый подведением под знак дифференциала:

умножим и разделим подынтегральную функцию на		5 и учтем, что
5dx d(5x) .
cos 5xdx cos 5x 1 5dx 1 cos 5x d 5x		1 sin 5x C.
5	5	5
На последнем шаге здесь использовано свойство инвариантности и
формула 5 из таблицы интегралов. Окончательно
I arcsin e x 3	1 e2x 1 sin 5x C.
	5

Метод интегрирования по частям

Интегрирование по частям в неопределенном интеграле производят по формуле:

udv uv vdu.

Чтобы вновь полученный интеграл vdu был проще исходного udv ,

нужно удачно выбрать выражения u и dv в заданном интеграле. Часто при этом удобно пользоваться правилами:

-если под интегралом стоит произведение многочлена на синус, косинус или экспоненту, то в качестве u берем многочлен;

-если подынтегральное выражение является произведением многочлена на какую-либо функцию от логарифма, арктангенса или арксинуса, то за u следует брать именно эту функцию.

4x3 2x arctgxdx.

Решение.

Обозначим

u arctgx ;

dv 4x3 2x dx;

тогда

du arctgx dx

dx

; v 4x3 2x dx x4

x2 .

Подставляя

эти

1 x2

выражения в формулу интегрирования по частям, получим:

4x

3

2x arctgxdx x

4

x

2

arctgx

x4 x

2

dx

1 x2

x2

x4

x2 arctgx

x2 1

dx x4

x2 arctgx x2dx

1 x2

x4

x2 arctgx

x3

C.

3

Иногда предварительно сделанная замена переменной упрощает задачу интегрирования по частям. Возможны ситуации, когда интегрирование по частям следует применить несколько раз.

Интегрирование дробно-рациональных функций от различных выражений

Чтобы проинтегрировать правильную рациональную дробь от аргумента x , ее следует предварительно разложить на сумму простейших дробей. Дробно-рациональная функция от тригонометрических выражений может быть сведена к алгебраической дробно-рациональной функции от нового

аргумента

t

с

помощью

одной

из

подстановок:

t sin x;

t cos x;

t tgx;

t tg

x

(”универсальная”

тригонометрическая

подстановка).

2

sin x

Пример 14 . Найти

I

dx.

1

sin x

Решение. Применим универсальную тригонометрическую подстановку

t tg

x

; при этом

sin x

2t

;

cos x

1 t2

;

dx

2dt

. Тогда

2

1 t2

1 t2

1 t2

sin x

2t

2dt

4tdt

I

1 t2

1 t2

.

1

sin x

2

2

2t

1 t

t 1

1

1 t2

Разложим дробь, получившуюся под интегралом, на сумму простейших дробей:

4t

At B

C

D

.

1

2

2

t

1

2

t

1 t 2

t

1

t

1

Приведем выражение в правой части к общему знаменателю и учтем,

что числители обеих дробей равны:

4t At B t 2

2t 1 C 1 t 2 t 1 D 1 t 2 или

4t A C t3 2A B C D t 2 A 2B C t B C D .

Приравняемкоэффициентыпри одинаковых степенях t вправой и левой

частях данного выражения:

t3 : 0 A C,

t2 : 0 2A B C D,

Исклю чим п ерем ен н ую

C, учиты вая, что C A :

t1 : 4 A 2B C,

t0 : 0 B C D.

A B D

0,

4,

2B

0.

A B D

Теперьиз второго уравнения B 2 , изпервого и третьегоуравнений:

A 0 , тогда и C

0, D B 2 . Итак,

2

2

2

dt

2

t 1

2

d t 1

2

I

dt 2

2

1

t

t

1

1

t

x

1

2arctgt 2

t 1 1

C 2arctg tg

2

C

1

2

x

tg

1

x

x

2

x

2cos

2cos

2

2

C x

2

C.

x

x

x

2

sin

cos

sin

x

cos

2

2

2

2

Определенныйинтеграл

Определенный интегралвычисляют по формулеНьютона-Лейбница:

b

f (x)dx F(x) ba F(b) F(a),

a

где F(x) - первообразная для f (x) , т.е. F (x) f (x) .

Если в определенном интеграле производится замена переменной, то надо найти пределы интегрирования для новой переменной. При вычислении определенного интеграла может также использоваться формула интегрирования

b		b
по частям: udv uv		ba vdu.
a		a
			41			dx
Пример 15. Вычислить I								.
					2x 1	34	2x 1
			1
						по формуле: t 4
Решение. Введем новую переменную t									2x 1 или
t 4 2x 1, откуда		4t3dt 2dx	(показатель			степени у новой			переменной

выбирается как наименьшее общее кратное показателей корней: в данном случае 4 – наименьшее общее кратное чисел 2 и 4). Из этой же формулы видно,

что если x 1, то t 4								2 1 1,							а при						x 41: t				4 82 1 3. Поэтому
			I 41							dx											3			2t3dt	23 t2 9 9dt
							2x 1 3						4		2x	1								2
				1																	1			t 3t	1			t 3
		3		3 t 3 dt											3		dt							3				3	d(t 3)
		2 t											9										2 (t 3)dt 9
							t 3										t												t 3
		1												2	1						3			1				1
																			3
																											13
																					9ln | t 3 |
										2 t					3t
												2
2		32	3	3					12										1											9ln		3
		2							2	3 1						9ln | 3 3 | 9ln |1 3 |													2 2			2	.

4.1.2. Методические указания по выполнению контрольной работы N4

Несобственные интегралы

Интеграл называется несобственным в одном из двух случаев: а) промежуток интегрирования бесконечен;

б) подынтегральная функция имеет бесконечные разрывы внутри промежутка интегрирования или на его концах.

Несобственный интеграл по бесконечному промежутку

Несобственным интегралом от функции f (x) по промежутку a,

называется предел

A

lim f (x)dx.

A a

Он обозначается символом f (x)dx.

a

Если этот предел конечен, то интеграл называется сходящимся, в случаях, если предел бесконечен или не существует, - расходящимся.

Аналогично определяется несобственный интеграл от функции f (x) по промежутку , a

a			a
f (x)dx		lim	f (x)dx.
	A		A
Наконец, несобственный интеграл по промежутку( , )
определяется в виде суммы	a
f (x)dx f (x)dx f (x)dx,
			a
где a - произвольное число,	при этом	f (x)dx сходится только тогда,

когда оба интеграла в правой части сходятся.

dx

Пример 16. Вычислить несобственный интеграл 0 x2 2x 2 .

Решение.

		dx		A	dx
0				lim
	x2	2x 2		A 0	x2 2x 2

lim arctg(x 1)		0A lim arctg(
A		A

A d(x 1)

lim (x 1)2 1

A 0

A 1) arctg(0 1) 2 4 4 .

Следовательно, данный интеграл сходится и равен 4 .

Для выяснения факта сходимости или расходимости несобственного интеграла часто используются следующие теоремы:

Теорема. Несобственный					интеграл f (x)dx сходится, если
					a
сходится интеграл		f (x)		dx .	В этом случае говорят, что интеграл
a

сходится абсолютно.

Теорема. Если на промежутке интегрирования функции (x) и f (x) непрерывны, неотрицательны и (x) f (x) , то из сходимости интеграла

f (x)dx

следует

сходимость

(x)dx ,

а

из расходимости (x)dx

a

a

a

следует расходимость f (x)dx.

a

Пример 17. Определить, сходится

или

расходится

несобственный

3 sin x dx .

интеграл

1

x

Решение. Заметим, что на всем промежутке интегрирования

3 sin x

2

0.

x

Рассмотрим интеграл

x

A

2

2

4

x

1A lim 4

A 4 .

dx

lim

dx lim

1

x

A

1

x

A

A

Рассмотренный интеграл расходится. Следовательно, по теореме 2, данный

несобственный интеграл также расходится.

Несобственный интеграл от неограниченной функции

Пусть функция f (x) непрерывна на промежутке a,b , а в точке b

имеет бесконечный разрыв: lim f (x) . Несобственным интегралом x b o

b	f (x) на промежутке a,b называется предел
f (x)dx от функции
a		b
	lim
		f (x)dx.
	0 o	a

Несобственный интеграл называется сходящимся, если указанный предел существует и конечен, и расходящимся в противном случае.

Аналогично определяется интеграл от функции, имеющей бесконечный разрыв на левом конце промежутка интегрирования.

1 x

32 x 12

Пример 18.Вычислить несобственный интеграл

dx.

x

0

Решение. Подынтегральная функция имеет бесконечный разрыв в

точке 0, поэтому

1

x

32

x

12

1

x

32

x

12

1

1

1

1

dx lim

dx

lim

x

2dx x

2dx

x

x

0

0 o

0 o

lim

2

x

3

2 2x

1

2

1

lim

2

2

3

2

2

1

2

2

2

.

2

0

o

3

0 o

3

3

3

Пример 19. Определить, сходится или расходится несобственный

интеграл

5

x cos x

3

dx .

Решение.

x2

9

Интеграл

является несобственным, так как

подынтегральная функция имеет бесконечный разрыв в точке

x 3.

На

всем промежутке интегрирования

x cos x

x

, т.к.

cos x

1 при x 3;5 .

x2

9

x2 9

5

x

Рассмотрим

интеграл

dx .

Сделаем

в

нем

замену

3

x2 9

t x2

9 ,

тогда

x2 t 2

9,

xdx tdt

и

t 0

при

x 3,

а

t 4 при

x 5. Тогда

	5	x	4 tdt			4
			dx	t	t	0	4.
		x2 9
	3		0

Этот интеграл сходится. Следовательно, исходный интеграл сходится абсолютно.

Геометрические приложения определенного интеграла

Рассмотрим приложения определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения и длин дуг кривых.

1. Вычисление площадей плоских фигур

y

Если

фигура

ограничена

сверху графиком

y f x

функции y f (x), снизу -

графиком

y (x),

сбоку -

прямыми

x a

и

x b

(рис.

4),

то ее

площадь S находится по формуле

b

O

y

x

x

S f (x) (x) dx .

a

a

b

Пример 20. Вычислить площадь круга

Рис. 4

радиуса R .

Решение. Круг определяется неравенствами

R2

x2

y

R2

x2 , R x R .

В

таком

случае

f (x)

R2

x2 , (x)

R2 x2

,

x изменяется от R до R . Тогда

R

R

S

R2 x2

R2 x2 dx 2 R

2 x2 dx.

R

R

x R sin t,

Сделаем

в

этом

интеграле

замену

тогда

dx R cos tdt,

R2

x2 R cos t,

t

2

при

x R

и

t

2

при

x R. Тогда

S

2

2R cos tR cos tdt 2R2

2

cos2 tdt 2R2 2 1 cos 2t dt

2

2

2

2

2

sin 2t

2

R

2

(1 cos 2t)dt R

2

R

2

2

.

t

R

2

2

2

2

2

Пример 21. Вычислить площадь фигуры, заданной неравенствами:

y 2 x2 , y x, y x.

Решение. Описанная фигура лежит под параболой и над биссектрисами 1-го и 2-го координатных углов (рис. 5). Для вычисления ее площади разобьем промежуток интегрирования на два:

y

0

1

x2 x dx

y x

y x

S

2 x2 ( x) dx 2

2

1

0

2x

x

3

x

2

0

2x

x

3

x

2

1

7 .

x

O

1

3

2

1

3

2

0

3

1

Рис. 5

В полярной системе координат площадь

y

f

,

сектора,

ограниченного

двумя

лучами

и кривой, заданной непрерывной функцией

f ( ), , (рис. 6), находится по формуле

x

S 1

f 2 ( )d .

O

Рис. 6

2

Пример 22. Вычислить площадь круга радиуса

R , используя полярные координаты.

Решение. В полярных координатах уравнение окружности радиуса R

с центром в полюсе имеет вид R 0 2 . Тогда для площади круга

имеем

2

S 1

R2

02

R2

R2d

2 R2 .

2

2

2

0

y

Пример

23. Найти площадь фигуры,

5

ограниченной

кардиоидой

r 2sin 3

и лучами

0 и

2

.

x

Решение:

O

3

Вид фигуры, ограниченной данной

кардиоидой,

представлен на рис.7. Согласно

1

условию,

требуется найти площадь заштрихованной

части фигуры, для которой полярный угол изменяется

Ðèñ.7

от 0 до

2

. Тогда искомая площадь будет равна

	1		1		4sin2 12sin 9 d
S		2 2sin 3 2 d		2
	2	0	2	0

	1	2		4		1 cos 2						1			2	2cos 2 12sin 11
	2					2		12sin 9 d				2
		0												0
					1	sin 2 12cos 11							1			11							11
					2					0	2		2			2		12					4		6.
	2. Вычисление длин дуг кривых
	Если плоская дуга задана параметрическими уравнениями
								x (t), y (t),						где t ,
и функции (t), (t)								имеют непрерывные производные, не обращающиеся в
ноль одновременно, то длина дуги
											2								2
																				dt.
								L (t)						(t)
	Пример 24. Вычислить длину окружности радиуса R .
	Решение. Окружность радиуса										R с центром в начале координат
задается						в		параметрическом											виде						уравнениями
x R cos t,						y R sin t, где t 0, 2 , тогда
						2										2						02 2 R.
						L	R2 cos2 t R2 sin2 tdt R dt Rt
						0											0							a x b , то
	Если дуга задана в явном виде уравнением y f (x),

b

L 1 f (x) 2 dx.

a

Пример 25. Вычислить длину окружности радиуса R , используя последнюю формулу.

Решение. Рассмотрим четверть окружности радиуса R с центром в начале координат, расположенную в первом координатном угле. Она задается

уравнением y

R

2

x

2

,

x 0, R .

Тогда

y

x

и для

R2 x2

длины окружности получаем

R

x2

R

dx

L 4

1

dx 4R

.

R2

x2

R2 x2

0

0

Этот интеграл является несобственным, так как подынтегральная функция имеет бесконечный разрыв на правом конце отрезка интегрирования. Вычислим его:

R

dx

R

dx

L 4R

lim 4R

2

2

2

2

0

R

x

0

0

R

x

x

R

lim 4R arcsin

4R

2 R.

0

R

0

2

Если плоская дуга задана в

полярных

координатах

уравнением

( ),

где функция

непрерывно дифференцируема

на

отрезке

, , а начальная и конечная точки дуги имеют полярные углы

и

соответственно, то длина дуги вычисляется по формуле

2

2

L

d

( )

( )

Пример 26.

радиуса R , используя

Вычислить

длину

окружности

последнюю формулу.

R с центром в полюсе системы

Решение. Окружность

радиуса

координат задается уравнением

R(0 2 ).

Тогда 0 и длина

2

2

02 2 R.

L

0 R2 d R d R

0

0

3. Вычисление площадей поверхностей вращения

a x b ,

Если плоская дуга AB задана

уравнением

y f (x),

причем

f (x) неотрицательна

и имеет непрерывную производную на

(a,b), то площадь поверхности,

полученной при вращении дуги AB вокруг

оси Ox , может быть вычислена по формуле

b

2

dx.

S 2 f (x) 1 f (x)

a

Пример 27. Вычислить площадь сферы радиуса R .

Решение. Сфера радиуса R может быть получена вращением

полуокружности

y

R2 x2 ,

x R, R ,

вокруг оси

Ox .

Тогда

y

x

R2 x2 и для площади поверхности сферы получаем

R

x2

R

S 2

R2 x2

1

dx 2 R dx 4 R2.

R

2

2

R

x

R

4. Вычисление объемов тел вращения

Если плоская дуга AB задана уравнением y f (x), a x b ,

причем f (x) неотрицательна, то объем тела, полученного при вращении

криволинейной трапеции, расположенной под дугой AB , вокруг оси Ox может быть вычислен по формуле

b
V f 2 (x)dx .
a	c y d ,
Если плоская дуга CD задана уравнением x ( y),

причем ( y) неотрицательна, то объем тела, полученного при вращении криволинейной трапеции, расположенной под дугой CD , вокруг оси Oy может быть вычислен по формуле

d

V 2 ( y)dy.

c

Пример 28. Вычислить объем шара радиуса R .

Решение. Шар радиуса R может быть получен вращением полукруга

y

R2 x2 ,

x R, R , вокруг оси Ox . Тогда для объема шара

имеем

R

R

R2 x

x

3

R

3

R

3

4 R3.

V

R2

x2 dx

R3

R3

3

3

3

3

R

R

Дифференциальное исчисление функции нескольких переменных

Переменная z называется функцией независимых переменных x, y на множестве E , если каждой паре ( x, y ) значений этих переменных из E

ставится в соответствие одно определенное значение z .

Аналогично определяются и функции большего числа переменных.

Частные производные

Для функции нескольких переменных вводится понятие частной

производной

по

каждому

из

аргументов.

Если

z f (x, y) ,

то по

'

z

f x0 x, y0

f x0

, y0

определению

zx

lim

-

частная

x

x

x 0

производная z по x в точке M 0 x0 , y0 .

Аналогично определяется и частная производная по y

'		z			f x0 , y0	y f x0 , y0
z y				lim					.
		y				y
				y 0

При вычислении частных производных все аргументы функции, за исключением той, по которой производится дифференцирование, считаются постоянными (константами). При вычислении частных производных применяются те же приемы, что и при вычислении обыкновенных производных.

Пример 29. Вычислить zx

и zy для функции z f (x, y) xy2 sin x .

Решение. Найдем zx .

Считаем

y2

величиной постоянной,

выносим его за знак производной.

Дифференцируем x sin x no

x как произведение.

y

'

2

'

2

2

sin x x cos x .

zx y

x sin x x y

x sin x x sin x

Для z'y получаем

x sin x y2 'y x sin x 2 y 2xy sin x.

z'y

Частные производные второго порядка - это частные производные от

производных первого порядка. Например:

z

z

2 z

2 z

x

x2

zxx'' ;

x

zxy'' .

x y

x

y

Если функция z f (x, y)

обладает в некоторой точке непрерывными

частными производными zxy

и

zyx , то эти производные равны. Аналогичный

факт справедлив и для производных более высоких порядков и для большего числа аргументов, что позволяет выбирать порядок дифференцирования.

Пример 30. Вычислить

3u

для функции u e x z sin y .

x y z

Решение. По определению частных производных высших порядков,

можно найти искомую производную следующим образом:

u

x

x

'

sin y

x

e

z sin y

(sin y) e

z

e

z

x

x

x

z

2u

u

sin y

x

1

x

e

z

cos y e

z ;

x y

z

z

y

x

y

3u

2u

1

x

1

x

1

x

x

z

z

z

x y z

cos y

z

e

cos y

z

2 e

z

e

z

2

z

x y

z

1

x

xe

x

x z

x

e

z

z

cos y

e

z

cos y.

2

3

3

z

z

z

Если функция y от x задана неявно уравнением F(x, y) 0 , то производная y

по x вычисляется по формуле:

F

dy

F '

(x, y)

x

x

,

dx

F

Fy'

(x, y)

y

где F '

(x, y) и F ' (x, y)

- частные производные от F(x, y) по x , y

x

y

соответственно.

Пример 31. Вычислить yx

и дифференциал dy ,

если

F(x, y) e y xy 0.

Решение. В данном случае F '

y, а F '

e y x . Тогда

x

y

yx'

y

;

dy

y

dx.

e y x

e y x

Если функция z от x , y задана неявно уравнением

F(x, y, z) 0, то

частные производные z по x , y могут быть вычислены изсоотношений

z

F

Fx' (x, y, z)

z

F

Fy' (x, y, z)

x

;

y

.

F

Fz' (x, y, z)

F

x

y

Fz' (x, y, z)

z

z

Полный дифференциал

Если функция

z f (x, y)

имеет непрерывные частные производные в

точке M (x, y) , то ее полным дифференциалом в этой

точке называется

выражение

dz xz dx yz dy .

Пример 32. Найти полный дифференциал dz в точке M0 0, 4 ,1 для

функции z(x, y) , заданной уравнением zy arctg(xz)

4

.

Решение. Поскольку функция z(x, y)

задана неявно, то ее частные

производные zx , zy

можно

найти,

используя

приведенные соотношения, где

F(x, y, z) zy arctg(xz)

4

. Тогда

z

x

F '

;

F '

z;

F '

y

.

x

1 x2 z 2

y

z

1 x2 z 2

В точке

M0 0, 4 ,1

Fx' M0 1,

Fy' M0 1,

Fz' M0 4 .

Следовательно,

в

этой

точке

z

4

,

z

4

и полный

x

M0

y

M0

дифференциал

dz M0 4 dx 4 dy 4 (dx dy).

Наибольшее и наименьшее значения функции нескольких переменных в ограниченной области

Если функция нескольких переменных определена и непрерывна в замкнутой ограниченной области, то она может принимать наибольшее и наименьшее значения либо внутри области в точках экстремума, либо на границе области.

Решение задач на нахождение наибольшего и наименьшего значений функции двух переменных z(x, y) в замкнутой ограниченной области D

рекомендуется проводить по следующему плану:

-найти точки внутри области, в которых выполняются необходимые условия экстремума zx 0 и zy 0 , вычислить значения функции в этих

точках;

-найти наибольшее и наименьшее значения функции на границе области (обычно этот этап решения сводится к поиску наибольших и наименьших значений функции одной переменной на отрезках);

-сравнить полученные значения функции, выбрать из них наибольшее и наименьшее.

Пример 33. Найти наибольшее и наименьшее значения функции

z 2x2 y2 6 y 1 в	замкнутой ограниченной области D , заданной
неравенствами y 4 x2 ;	y 0.

y

4 M2

3 M1

Решение. Исследуемая область D изображена на рис. 8.

l. Ha первом этапе найдем стационарные точки функции z внутри области D и значения функции в

этих точках. Для этого частные производные zx 4x и zy 2 y 6 приравняем нулю и решим полученную

A O M3

C x

систему уравнении:

4x 0

. Эта система имеет

2

2

6

0

2 y

Рис. 8

единственное решение x 0,

y 3. Стационарная

точка M1(0,3) расположена внутри области и z M1 8.

2. Исследуем функцию на границе области:

а)

В

точках

параболы

y(x) 4 x2

( 2 x 2)

функция

z

после подстановки y y(x) становится

функцией одной

переменной.

Исследуем

эту функцию

z 2x2 4 x2 2

6 4 x2 1 x4 7

на

замкнутом

промежутке

2 x 2 : zx' 4x3 0 x 0;

0 ( 2; 2).

При этом y 4 x2

x 0

4. Значит, заданная функция имеет на участке

M2 (0, 4) .

параболы

единственную

стационарную

точку

Вычислим

z M2 7.

y 0

( 2 x 2) функция z принимает вид:

б) На отрезке прямой

z 2x2 1.

Найдем

ее

стационарные

точки:

zx' 4x 0 x 0;

0 ( 2, 2).

При этом

y 0. Значит, заданная функция имеет на отрезке

прямой единственную стационарную точку M3 (0, 0). Вычислим z M 3 1.

в) Вычислим значения функции z в точках A( 2, 0)	и C(2, 0) : z( A) 9,
z(C) 9.
3. Сравнивая найденные значения функции z(x, y) :
z(M1 ) 8; z(M 2 ) 7; z(M 3 ) 1; z( A) 9;	z(C) 9,

делаем вывод, что данная функция достигает в заданной области наименьшего значения в точке M1 , а наибольшего в точках A и C .

4.1.3.Задания на контрольные работы №№ 3-4

Вконтрольных работах студент должен решить задачи, выбрав их номера из таблицы по двум последним цифрам своего шифра и первой букве фамилии.

Например, студент Захаров, шифр 17-0025, выполняет в контрольной

№3 - 102,115,125,135, 142; в контрольной №4 - 152,165,175, 182, 195.

	Последняя			1	2	3	4	5	6	7	8	9	0
	цифра шифра
	Номер		3	121	122	123	124	125	126	127	128	129	130
	контроль			131	132	133	134	135	136	137	138	139	140
	ной		4	161	162	163	164	165	166	167	168	169	170
	работы
	Предпоследняя			1	2	3	4	5	6	7	8	9	0
	цифра шифра
	Номер		3	101	102	103	104	105	106	107	108	109	110
	контроль			141	142	143	144	145	146	147	148	149	150
	ной		4	151	152	153	154	155	156	157	158	159	160
	работы			181	182	183	184	185	186	187	188	189	190
	Первая буква			А,И	Б,О	В,Н	Г,Ф	Д,З	Е,М	Ж,С	К	П	У,
													Ш
	фамилии			Т	Ц	Х	Я	Л	Р	Ч	Э	Щ	Ю
	Номер		3	111	112	113	114	115	116	117	118	119	120
	контроль			171	172	173	174	175	176	177	178	179	180
	ной		4
				191	192	193	194	195	196	197	198	199	200
	работы

Задание на контрольную работу № 3.

В задачах 101-110 найти пределы, пользуясь правилом Лопиталя.

101.	lim	e5x cos 5x	,	102.	lim	x arctgx					,
		e2 x cos 2x					x3
	x 0				x 0
	lim xsin x ,							2
103.				104.	lim		ex2			,
						x2
	x 0 o				x 0

105.

lim

1

tgx

106.

lim

e2 x2 tg

x

,

,

2e

x 0

o x

x e

x ex

ex e x 2x

107.

lim

,

108.

lim

x sin x

,

2

x 0

x 0

x 1 x

1

ex e x

109.

lim

(ex x) x ,

110.

lim

.

x

x 0 sin x cos x

В задачах 111-120 исследовать функцию и построить ее график.

111.	y	(x 1)2				,		112.		y					x			,
		x2 1										1 x3
113	y x3 x 1 2 ,							114.		y			3 2x						,
												(x 2)3
115.	y	2 4x2				,	116.		y		4x3						,
		1	4x2								x3				1
117.	y	4x3 5				,	118.	y		x3				,
			4x							x2	1
119.	y	x2			,		120.	y		x2	1			.
		x	1							x2	1

В задачах 121-130 найти неопределенные интегралы. Результат проверить дифференцированием.

121.			cos 2x	x2 1 4x					dx,	122.
				x2	1
123.			cos(3ln x) x2 4			dx,				124.
				x
125.			5 sin x cos x 4ctg3x						dx,	126.
			sin2 x
127.		7 3 sin x dx,								128.
			tgx
129.			sin x 3ctgx cos x				dx,			130.
			sin5 x

		2x 5	3 arcsin x			dx,
			1	x2
		3 2tgx e4tgx
					dx,
		cos2 x
	2arctgx			4 5 arctgx			dx,
			1	x2

sin ln(x 7) 6 dx,

x7

tgx 3 cos x dx. 2ctgx

В задачах 131-140 найти неопределенные интегралы, используя для вычислений формулу интегрирования по частям.

131.	x 3x dx,	132.
133.	x ln(x2 1)dx,	134.
135.	xarctg3xdx,	136.

x2 e3xdx, x sin 4xdx,

arcsin x dx, 1 x

137. arctg	7x 1dx,	138. arcsin x dx,
		x

139.x2 3x 2 ln xdx, 140. 4x3 6x 7 ln xdx.

Взадачах 141-150 вычислить определенные интегралы, используя подстановки, указанные в скобках.

141.		3		dx		t tgx ,
				cos3 x sin x
		4
3				sin xdx		t cos x ,
142.
			3cos x cos2 x
	0

		ln 3							ex 2 ex
	143.																dx
									ex 1
		ln 2
	144.	2									dx
						3cos x 4sin x
		0
	145.	4									dx
							sin2 x 5cos2 x
		0
	146.	7							dx
							3 x 1
		0 1
	147.	3				4 x2							3			2 dx
		1
	148.	16							1		4	x						dx
		1							x 4 4 x3
	149.	ln 2							e	4x						dx
									5 2e4x
		0
	150.	61										dx
									x 3 3 (x 3)2
		2

t ex 2 ,

		x
	t tg			,
		2

t tgx ,

t 3 x 1 ,

x 2sin t ,

t 4 x ,

t 5 2e4x ,

t 6 x 3 .

Задание на контрольную работу № 4

В задачах 151-156 вычислить несобственный интеграл или доказать его расходимость.

		dx	1			xdx						x 5
151.			152.					153.					dx
		x x 1			1 x4					x	2	2x 2
	2		0					1
	1			0				1				dx
154.	ln xdx		155.			arcsin x dx		156.
												ln2 x
	0	x	1			1 x2		0 x 4

В задачах 157-160 доказать, используя признак сравнения, сходится или расходится несобственный интеграл.

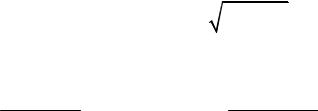
	2 cos3	x dx	4		dx
157.			158.
				3	x2 2x
1	x		2

159.sin x 2 dx 160.

x 12

161.Найти площадь плоской фигуры, ограниченной линиямиdxx3 1 ex20

	y	x 2 2 ,	y 2	x 2	2 .Сделать рисунок.
	162.	Найти	площадь	плоской		фигуры, ограниченной линиями
	y sin(2x),		y 0,	x 0,	x		. Сделать рисунок.
						4

163.Вычислить площадь шарового пояса, получаемого при вращении

вокруг оси Ox дуги окружности x2 y2 4

( y 0) между точками с

абсциссами x 12 и x 1. Сделать рисунок.

164.	Определить длину дуги кривой y ln sin x , где		x	.
		3		2

165.Определить длину дуги одной арки циклоиды:

x 3 t sin t , y 3 1 cos t , где 0 t 2 .

166.Вычислить площадь фигуры, ограниченной одной аркой циклоиды

иосью Ox : x 4 t sin t , y 4 1 cos t , где 0 t 2 .

167.Вычислить объем тела, образованный вращением вокруг оси Ox

фигуры, ограниченной линиями y cos 3x , y 0, x 0, x		. Сделать
	6

рисунок.

168.Вычислить площадь поверхности, образованной вращением

	вокруг оси Ox кривой y	x3	от	x 0	до x 2 . Сделать рисунок.
		3
	169. Вычислить объем тела, образованный вращением вокруг оси Oy

фигуры, ограниченной линиями xy 4, y 1,	y 4, x 0. Сделать рисунок.
170. Найти длину дуги кривой y 32	2 x 3 от x 1 до x 2 .

2z

x y

В заданиях 171-174 для функции z x, y убедиться, что

2z .y x

171. z 8x2 xy 2 y2 16x y 1.

172. z 55 15x 2x2 xy 2 y2 . 173. z x3 6xy 8y3 5.

174. z 1 6x x2 xy y2 .

В заданиях 175-177 найти значение 2z в точке A.

x y

175.	z x3 6x2 y y2 39x 18y 20,							A 1;0 .
176.	z 3x3 9xy2 3y3 10,					A 1;1 .
177.	z x2 x2 y2 y2 x y 1,						A 0;1 .
В заданиях 178-180 найти значение			2u		в точке A.
		y z
178.	u z2 zy2 y2 6z 9 y 2,						A 1;1; 2 .
179.	u zx3 zy3 3xy 2z,					A 1;1;0 .

180.

u z 8xz 2 y 2x2

2 yz 4 y2,

A 1;0;1 .

В заданиях 181-185 найти в точке A дифференциал функции y x ,

заданной неявно.

1

y

sin x,

;

181. e

x

A

2

2

.

182.

ln 2x y 2

sin

x y ,

A(1;1).

x

183.

ctg

y

2

x

,

A

;1 .

y

2

184.

arcctg x y

x y ,

A 1;0 .

4

185.

3y 2x 2 xey ,

A 2;0 .

В заданиях 186-190 найти в точке A полный дифференциал функции z x, y , заданной неявно.

	z3 x e	y		A 1;3;e .
186.		x	,
187.						,
	sin xy x tg z						A 1;0;	4	.
					4

188.	cos xz ln 2x y ,
			A 1;1;	.
				2
189.	yexz 2 e 2x z,		A 1;e;0 .
190.	z3 2x3 3zxy,	A 1;1; 2 .

В заданиях 191-200 найти наибольшее и наименьшее значения функции z x, y в указанной замкнутой области D . Сделать рисунок

области.

191.

z x2 y2 4xy 4,

: 0 x 4,

0 y 4.

D

192.

z x2 2 y2 1,

: x y 3,

x 0,

y 0.

D

193.

z x2 2 y2 4xy 1,

: 1 x 1,

0 y 2.

D

194.

z x2 y2 4xy 6x 2 y,

: y 4 x,

x 0,

y 0.

D

195.

z 2x3 4x2 y2 2xy,

: y x2,

y 4.

D

196.

z 10 x2 2xy,

: 0 y 4 x2.

D

197.

z x2

y2 2xy 2x 2 y 3,

: x 2,

0 y x 2.

D

198.

z x2

xy 2,

: 4x2 4 y 0.

D

199.

z x2

xy 3x y,

: 0 x 2,

0 y 3.

D

200.

z 3 2x2 xy y2,

: x 1,

0 y x.

D

4.2. Текущий контроль Тестовые задания

Тест 1 (тема 1.1)

1. Если f x sin x,			;			, то из формулы Лагранжа следует, что
	x	6		2

f' c , где c ; , равна

6 2

A) 0 ;

B)

3

;

C) 1;

D) 32 .

2

2. Многочлен Маклорена Pn x для функции

f x ln 1 x

имеет вид:

A)

1

x

x2

...

xn

;

B) 1

x2

x4

...

xn

cos

n

;

1!

2!

n!

2!

4!

n!

2

C)

x

x2

x3

... 1 n 1

xn

;

D)

x

x3

x5

...

xn

sin

n .

2

3

n

2x

3!

5!

n!

2

3. Найти предел по правилу Лопиталя:

lim

1

...

sin x

x 0

A) ln 2 ;

B) 0 ;

C) 1;

D)

1

.

ln 2

4. Найти предел, применяя правило Лопиталя несколько раз:					lim	x3	...
A) 1;		B) 0 ;	C) ;	D) 6 .	x ex
5.	С помощью тождественного преобразования и правила Лопиталя найти
предел:	lim	x ln x ...
	x 0 0	B) 1;	C) 0 ;	D) 1.
A) ;

6.Применяя основное логарифмическое тождество и результат

предыдущего примера найти предел:			lim	xx ...
A) 0 ;			x 0 0	D) 1.
	B) ;	C) e ;

Тест 2 (тема 1.2)

1. Функция f (x)	x2 1
A) возрастает при x ; ;		B) убывает при x ; ;

C)убывает при x ;0 и возрастает при x 0; ;

D)постоянна при x ; .

2.Для функции f (x) x2 1 найти точку экстремума:

A) x 1;	B)	x	;	C)	x 0	; D ) точки экстремума нет.
0		0	4		0
3. Из уравнений y x (I) и y x (II) выбрать уравнения асимптот
графика функции	f (x)	x2	1 :

A)(I) – асимптота и (II) - асимптота;

B)(I) – не асимптота и (II) – не асимптота;

C)(I) – асимптота, а (II) – не асимптота;

D)(I) – не асимптота, а (II) - асимптота.

4. Для функции f (x) x2

1 точка x

0 есть:

0

A) точка максимума;

B) точка разрыва;

C) точка минимума;

D) точка перегиба.

5. График функции

f (x)

x2 1 является выпуклым вниз на

промежутке:

;

A)

B) 0;

;

C)

;

;0 ;

;

D)

2

2

.

	6. Наибольшим значением функции		f x 4x3			8x2	4x на промежутке
	0;1
	будет:
	A) 2725 ;	B) 94 ;	C)	9		;	D) 1627 .
				16

																													Тест 3 (тема 2.1)
	1. Найти произведение 2(2 3i)(3 2i)
	A) 6 4i ,														B) 12 6i ,																			C) 24 10i ,													D) 12 12i .
	2. Записать комплексное число z																																			3 i								в алгебраической форме
																																		(1		i)(1						2i)
	A)	4		3 i ,											B)				4							3 i			,					C) 1 2i,													D) 6 i .
		5		5															5							5
	3. Записать в тригонометрической форме комплексное число z 1 i
	A)	z			2									isin																				B) z							2					isin
								cos				4										4				,																	cos		4				4		,
	C)	z cos								isin								,																D) z							2				3		i sin			3
								4								4																											cos		4						.
																																																			4
	4. Вычислить по формуле Муавра (1 i)10
	A) 32i ,														B) 4(1 i) ,																			C) 64,									D) 8i .
	5. Найдите все значения корня 3 8
	A) z1 2, z2 2, z3 i 3 ,
	B)	z1 2, z2										3			i							3				, z3						3	i			3		,
																				2										2						2
												2
	C) z1 2, z2 1 i																		3, z3 1 i 3 ,
	D) z1 2, z2 2, z3 i 3 .
																													Тест 4 (тема 3.1)
															1						1								4
	1. Вычислить																													dx.
														3		x				x			3						x
		3 3		x	2					1		8 x C;																								3 3					2			1			1
	A)																																						x			8x2						C;
																																		B) 2
		2							2x2																																					2x2
	C)	3	x					1			8			x C.
		2					2x			2
													arcsin x											3
	2. Вычислить																										dx.
													2
																1 x
	A)	arcsin x 2																												B)		arcsin x 4									C;
					2						C;																							4
	C) arcsin x								1 x2					C.

3. Вычислить x x2 1 4 dx.

		x	2	1			3							x	4			x	2
A)							C;					B)									C;
				3										4				2
4. Вычислить x2												cos x3 dx.
A) 3sin x3 C;												B) 3sin x3 C;
5. Вычислить 3x3												2dx .
											x	1
A) ln | x3 1| C;												B) 3ln | x3 1| C;
6. Вычислить x2												8 x3 dx.
	9				8	x		3		3	C;								2			8	x	3		3
A) 2																B)			9
							3
C) 6 8 x3 2 C.

C)	x2 1 5	C.
	10

C)13 sin x3 C.

C)13 ln | x3 1| C.

C;

Тест 5 (тема 3.3)

1. Найти

x3dx

.

2 x

2

1

3

1

3

A) 2 2 x2

2 x2 2 C;

B) 2 2 x2

2 x2 2

C;

3

3

3

1

C) 2 2 x2

2 x2 2 C.

3

2. Найти

cos 4 x

dx.

4 3

x

A) 14 sin 4 x C;

B) 4sin 4

x C;

C) 4sin 4

x C.

C)

5

arctg

x2 3

C.

2

5

3. Найти xe 2 x dx.

1 xe 2 x

1 e 2 x C;

2 x

4e

2 x

C;

B)

A) 2xe

2

4

C)12 xe 2 x 14 e 2 x C.

4.Найти x2 ln xdx.

x3

x3

x3

x3

A)

ln x

C;

B)

ln x

C;

3

3

3

9

x3

x3

C)

ln x

C.

3

9

5. Найдите значения постоянных A и B в разложении

5x 7

A

B

.

x 1 x 2

x 1

x 2

A) A 2,	B 3;
C) A 2,	B 3;

6. x 2 x22 x 1 dx ...

	A) ln | x 1|			4		C;
				x 2
		4
	C)		ln | x 1|			C.
		x 2

B) A 2,	B 3;
D) A 4,	B 2.

	B) ln | x 1|	4	C;
		x 2

			Тест 6 (тема 3.4)
	1. Если для непрерывной на отрезке 2;7 функции f (x) известно, что
3		7	7
	f (x)dx 1,	f (x)dx 5,	то f (x)dx равен
2		3	2

A) 4 ,	B) 6 ,				C) 4,	D) 5.
			2			0
2. Известно, что				f (x)dx 5. Тогда f (x)dx равен
			0			2
A) 10 ,				B) 5 ,		C) 5,	D) не существует.
								x	t2	dt , то
3. Если для всех x 0 выполняется равенство F(x) e											F (x)
равна								0
A) xe x2 ,	2			B) e t2 ,		C) e x2 ,		D) te t2 .
4. Вычислить x				2 xdx ...
A) 1415 ;	1			B) 1415 ;		C) 32 .
	1			x3	dx ...
5. Вычислить
			4 x2
	0
A) 16 9 3	;				B) 16 9 3	;	C)	3 9 3 .
3					3			3

			e	x ln xdx ...
	6. Вычислить
			1
	A)	e3 4	;	B)	9 e3 4	;	C)	2 e3 4 .
		9			2
								9

Тест 7 (тема 3.4)

1. Найти площадь фигуры, ограниченной линиями y x2; x y 2 .

A)	7	;	B) 6	5	;	C)	9 .
	6			6			2

2. Вычислить объем тела, полученного при вращении вокруг оси Ox

фигуры, ограниченной синусоидой			y sin x,	y 0 0 x .
	2	B) 2;		2	1
A)	2 ;		C)	2	2 .

3. Вычислить площадь поверхности, образованной вращением вокруг оси

Ox дуги кривой			y			1	x	3	;0	x 2; y 0 .
						3
A)	3									B)	3			3
	152	1			;						172	1	;	C) 172	1 .
3										9

4. Используя формулу S 1 2 r2d для площади криволинейного

2 1

сектора, заданного в полярных координатах, получим, что площадь области, ограниченной кардиоидой r 1 sin и лучами 1 0 и 2 , равна

A)

3

2;

B)

3

C)

3

;

D)

3

2.

4

2

tB

4

4

5. Используя формулу l

x'

(t)

2

y'

(t) 2 dt

длины дуги AB ,

t

t

tA

x (t),

заданной параметрически где t tA,tB , вычислить длину дуги AB

y (t),

циклоиды	x 2(t	sin t),	где tA 0,		tB .
		cost),
	y 2(1
A) 8;		B) 8		C) 4;		D) 2.

Тест 8 (тема 3.5)

dx

1.

Вычислить несобственный интеграл

или установить его

x ln x 3

расходимость

e2

A)

1 ;

B)

1

;

C)

1

;

D) интеграл расходится.

8

4

2

dx

2.

Вычислить

несобственный

интеграл

1

x

или

установить

его

расходимость

C) 1;

D) .

A) 0;

B) 1;

3.

Вычислить

несобственный

интеграл e xdx

или

установить

его

расходимость:

0

B) 1;

C) 0;

A) интеграл расходится;

D) 1.

0

sin xdx

4.

Вычислить

несобственный

интеграл

или

установить

его

расходимость:

B) 1;

C) 0;

A) интеграл расходится;

D) 1.

5.

Исследовать

сходимость

несобственного

1 cos2 x

,

интеграла

3 x

3

1

dx.

сравнивая его с интегралом

3 x

3

A) интеграл расходится;

B) интеграл сходится;

C) исследование с помощью такого сравнения невозможно.

1

dx

6.

Вычислить

несобственный

интеграл

или

установить

его

1 x2

расходимость

0

A) 2 ;

B) 4 ;

C) ;

D) интеграл расходится.

Тест 9 (тема 4.1)

1. Значение функции

u

x2 y xz

2

z

в точке

A( 1, 2,1)

равно

x3 z

3x

A)

11

;

B) 7 ;

C)

4

;

D)

1 .

6

6

3

2

2. Область задана системой неравенств x 0, y 0, x y 2.

A 32 ; 12 будет для области

A) внутренней;	B) граничной;	C) внешней.
3. Точка M(1,1)	для области определения функции z		x2 y2 4
A) внутренней;	B) граничной;	C) внешней.

4.Функция z x2 y2 на множестве x 2, 1 y 1

A)ограничена сверху, но не ограничена снизу;

B)ограничена снизу, но не ограничена сверху;

C)ограничена;

D)не ограничена ни сверху, ни снизу.

	5. Функция	z	x2	y2	1
			(x 1) x2		y
	A) непрерывна;					B) имеет одну точку разрыва;

C) имеет две точки разрыва; D) имеет линии разрыва.

Точка

будет

Тест 10 (тема 4.2)

1. Частная производная z y

функции z ln x3 2xy

в точке

M0 (1; 0)

равна

D) 12 .

A) 1;

B) 3;

C) 2;

2. Дифференциал функции z x2 x y3

в точке M 0 ( 1;1)

равен

A) 5dx 3dy;

B) 5dx 3dy;

C) 3dx 5dy;

D) 3dx dy.

3. Для функции

u x2 2xy ky2

будет выполняться

2u

2u

при k

x2

y2

равном

A) 3;

B) -1;

C) -2;

D) 1;

E) 2.

4.

Смешанная производная

u 2

функции

u ex2 y x2z

в

точке

xy

M0 (2; 4; 1)

равна

A) -2;

B) 1;

C) 2;

D) 4.

1

5. Функция z(x, y)

xy

z x z2

задана неявно уравнением

2 . В

точке

1

z

равна

A

2

;2;1 частная производная

y

A) 6;

B) -6;

C) 1

;

D) 1 .

6

6

Тест 11 (тема 4.4)

1. Уравнением касательной плоскости к поверхности

z f (x, y)

в точке

M

0

x , y , z

0

является

z z

0

f '

x , y x x f '

x , y

y y

.

0 0

x

0 0

0

y

0 0

0

Поэтому уравнение касательной плоскости к поверхности

z 3x2

4 y2 5

в

точке 1;1; 2

имеет вид

A) 6x 8y 14 0 ;

B) 6x 8y z 0 ;

C) 6x 8y z 2 0 ;

D) 6x 8y z 12 0 .

2. Нормаль к поверхности

z f (x, y) в точке

M0 x0 , y0 , z0

задается

уравнениями

x x0

y y0

z z0

.

Поэтому

уравнениями

zx' x0 , y0

z'y x0 , y0

1

нормали к поверхности z 3x2

4 y2 5

в точке 1;1; 2

будут

A)

x 1

y 1

z 2

;

B)

x 1

y 1

z 2

;

6

1

6

1

8

8

C)

x 1

y 1

z 2

;

D)

x 1

y 1

z 2

.

11

11

13

3

4

6

3. Дана вектор-функция a t t i 2sin t

j 3cost k . Тогда ее производная

a (t) равна

1

1

1

A)

i

j

k

;

B) t i

2sin t

j 3cost k

;

t

2sin t

3cost

D) i 2cost j 3sin t k .

C) i 2cost

j 3sin t k

;

4.

Если

закон движения

материальной

точки задан в виде

(t) 2t

2

3

s

i

3 j t

k , то вектор ускорения этой материальной точки в момент

времени t 2 равен

B) 4i 3 j 12k ;

A) 8i

3 j 12k ;

C) 8i

12k ;

D) 4i 12k .