4.3 Вираз нелінійності через коефіціенти Уолша-Адамара

Задля зручності, у виразі перепозначимоічерез та відповідно. Нехай також і , де та  відповідно кількість нулів та кількість одиниць у векторі .

Очевидно, однозначно визначає відстань Хемінга між і, а також кількість аргументів, на яких ці функції співпадають.

З системи , , випливає, що , а .

Число  ціле, оскільки .

Зауважимо також, що , оскільки .

Покажемо тепер, що відстань від функції до множиниможна записатиу виді .

Оскільки , то,.

Таким чином, , , а .

Якщо , то .

Якщо , то .

Тому, у загальному випадку, .

Повертаючись до старих позначень та враховуючи, що ,, , , отримаємо .

Звідси випливає, що чим більше абсолютна величина коефіціента Уолша- Адамара, тим менша відстань функції до пари афінних функцій , тим гірший параметр .

Таким чином: , ,.

Функція називається афінним статистичним аналогом функції , якщо при випадковому та рівноймовірному виборі аргументів імовірність співпадіння їхніх значень.

Очевидно, ймовірності можна обчислити через коефіціенти ,виходячи з співвідношення : .

Послідовність , де аргументи лексікографічно впорядковані, називається статистичною структурою функції .

Зауваження. Нехай - множина рівноймовірних булевих функцій від чотирьох змінних. Відомо, що для кожної функціїіснує афінний статистичний аналог, що співпадає зз імовірністю не менш.

4.4 Оцінка нелінійності через коефіціенти Уолша-Адамара

Знайдемо тепер оцінку , виходячи зі значення .

Оскільки , то

.

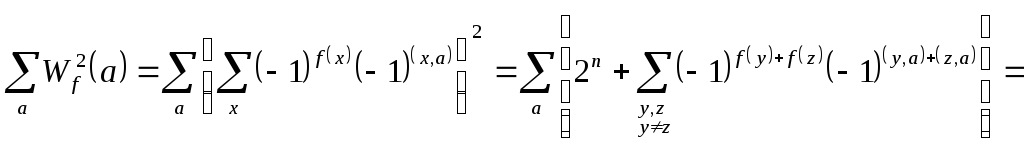
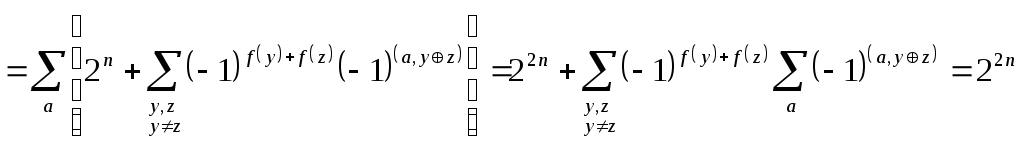Тут кожна внутрішня сума перетворюється в нуль при.

Дійсно, показник дорівнює кількості одиниць у векторі на місцях, що відповідають номерам одиничних компонент вектора, який від не залежить.

Оскількі у сумі задіяни всі векторів ,це означає, що величина приймає парні та непарні значення у рівній кількості випадків.

Далі. Припустимо, що .Тоді ,що, за попереднім, неможливо. Таким чином, для довільної булевої функції , ,звідки випливає:

.

У випадку, коли , прийме максимальне (найкраще з можливих) значення . При цьому, оскільки є цілим числом, - обов’язково парне.

Виявляється, що існують булеві функції з нелінійністю , для яких всі коефіцієнти Уолша-Адамара дорівнюють, наприклад,.

Такі функції називаються бент-функціями (bent functions).

0	0	0	0	0	0	0
0	1	0	1	0	1	0
1	0	0	0	1	1	0
1	1	0	1	1	0	1
→		2	2	2	-2

4.5 Максимально нелінійні функції

Нелінійність функції залежить, до того ж, від .

Функція називається максимально нелінійною, якщо значення досягає максимально можливого значення для булевих функцій від змінних (може бути непарним). Актуальною задачею залишається опис класу функцій для яких , у залежності від .

Відомо, що у випадку множина бент-функцій і множина максимально нелінійних функцій спідпадають, тобто .

Твердження. Нехай - булева функція відзмінних. Функціяє максимально нелінійною, тоді і тільки тоді, коли

, де і .

Доведення є вправою на розуміння позначень та визначення нелінійності.

Мінімум у правій частині рівності вибирає мінімальне за модулем значення серед тих коефіціентів Уолша-Адамара, які визначають значення нелінійності для відповідної функції. Оскільки чим менше це значення, тим більше нелінійність, то визначає значення нелінійності деякої функції, яке не може бути перевищено.

Рівність правої і лівої частини вказує на те, що , тому, за визначенням, функція - максимально нелінійна.

При аналізі властивостей булевих функцій, зокрема, нелінійності, може виявитися корисним поняття афінної еквівалентності.

Перетворення де- зворотна матриця (афінна заміна змінних) називається афінним перетворенням простору . Перетвореня є взаємно однозначним, тому являє собою перестановку векторів простору .

Таким чином, якщо у табличному записі переставити список арументів і не змінювати вектор значень, то отримаємо табличний запис нової функції, у якому лише упорядкування аргументівне буде лексикографічним.

Якщо ми тепер у цьому запису переставимо рядки (враховуючи вектор значень) так, щоб аргументи були лексикографічно впорядковані, то отримаємо коректний табличний запис , у якому вектор значень відрізняється від вектора значеньвідповідною перестановкою.

Очевидно, ця перестановка залежить тільки від параметрів і, тобто, при афінній заміні змінних координати векторів значень всіх функцій відзмінних переставляються однаковим чином.

Це показує, наприклад, що. Тому, зокрема, при афінній заміні змінних властивість рівноймовірності булевої функції зберігається.

Подібні властивості називаються інваріантними відносно афінної заміни змінних.

Функції іназиваються афінно еквівалентними. Булеві функції розбиваються на класи еквівалентності, тобто сукупності функцій, які еквівалентні до однієї функції, що називається твірною класу.

Якщо твірна володіє властивістю, що є інваріантною відносно афінної заміни змінних, то ця властивість притаманна всім функціям класу. Це суттєво полегшує аналіз булевих функцій.

Виходячи з подібних міркувань, можна довести аналогічні теореми відносно деяких інших властивостей булевих функцій.

Так, можна довести, що при афінній заміні змінних довільна афінна функція переходить в афінну.

Виходячи з цього твердження і визначення нелінійності, ми можемо зробити висновок, що нелінійність булевої функції є інваріантною відносно афінної заміни змінних.

Крім того, можна довести, що вектор абсолютних величин коефіціентів Уолша-Адамара ,, не змінюється при афінній заміні змінних.

Таким чином клас максимально нелінійних булевих функцій є інваріантним відносно афінної заміни змінних.

Як важливий факт відмітимо те, що бент-функції не є рівноймовірними.

Дійсно, , і для кожного . Зокрема, для ,і .

Але, якщо - рівноймовірна, то , що неможливо.

Тому у криптографічних застосуваннях використовуються методики побудови рівноймовірних булевих функцій з нелінійністю, що наближаєтся до максимальної: прита

при .

Для цього використовуються окремі критерії і результати, наприклад, такі, як наведено нище.

Теорема. 6.4. Нехай - довільна перестановка елементів простору,,- довільна булева функція відзмінних. Тоді булева функціявідзмінних видує максимально нелінійною.

Для вивчення инших критериїв, нам потрібно ввести деякі нові визначення, такі, як підфункції та похідні булевої функції.

Приклад.

Теорема 6.5. (Критерій Ротхауза). Булева функція відзмінних максимально нелінійна тоді і тільки тоді, коли коли її похідна за довільним напрямкомє рівноймовірною.