0887579_C36AB_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat

Порівнюючи формули (1.25), (1.31)—(1.33) та (1.44), (1.45), помітимо аналогію між рядом Фур’є і інтегралом Фур’є: знаку суми ряду Фур’є від-

повідає знак інтегрування, коефіцієнти an , bn ряду замінено функціями a(ω), b(ω). За аналогією з рядом Фур’є кажуть, що формула (1.45) дає розклад функції f (x) на гармоніки з частотами ω, що неперервно змінюються

від 0 до +∞ . Закон зміни амплітуд залежить від ω і визначається фор-

мулами (1.44).

Зауваження. Не всі функції можна розкласти в інтеграл Фур’є. Так, найпростішіфункції sin x, cos x, xn неабсолютно інтегровні(невлас-

∞

ний інтеграл ∫ f (x) dx розбіжний), томунерозкладаютьсявінтегралФур’є.

	−∞
	4.2. Інтеграл Фур’є для парних і непарних функцій
Нехай	f (x) ― парна функція, тоді f (t) cos ωt						також парна, а функція
f (t) sin ωt	непарна. Для непарної функції f (x) добуток f (t) cos ωt є не-
парною функцією,		f (t) sin ωt — парною. У цих випадках формули (1.44),
(1.45) набувають простішого вигляду (табл. 5)
									Таблиця 5
Властивість функції		f (x)	f (x) — парна функція				f (x) — непарна функція
				∞				∞
Інтеграл Фур’є			f (x) = ∫a(ω)cosωxdω				f (x) = ∫b(ω)sin ωxdω
			0				0
Коефіцієнти інтеграла				2 ∞			a(ω) = 0,
Фур’є			a(ω) = π ∫ f (t)cosωtdt,					2 ∞
				b(ω) = 0			b(ω) = π ∫ f (t)sin ωtdt
			0						0

4.3. Інтеграл Фур’є в комплексній формі. Перетворення Фур’є

Нехай функція f (x) зображується інтегралом Фур’є за формулою (1.45). Скориставшись формулами

	cos ωx =	eiωx + e−iωx	, sin ωx =	eiωx − e−iωx	,
		2		2i

101

інтеграл Фур’є можна звести до вигляду

			1	∞
		f (x) =		∫ F(ω)eiωx dω,
			2π
				−∞
	де

∞

F(ω) = ∫ f (t)e−iωt dt.

−∞

Із формул (1.46) та (1.47) випливає, що

	1	∞	∞		−iωx		iωx
f (x) =			∫	f (t)e		dt e		dω.
	2π	∫
		−∞	−∞

(1.46)

(1.47)

(1.48)

Праву частину формули (1.48) називають інтегралом Фур’є в комплексній формі для функції f (x) .

Функцію F(ω) , яка визначається формулою (1.47), називають пере-

творенням Фур’є функції f (x) . Формула (1.46) дає обернене перетво-

рення Фур’є для функції F(ω) .

Функцію f (t) ще називають оригіналом, а функцію F(ω) ― її зобра-

женням або Фур’є-образом.

Формулу Фур’є (1.45) можна подати у симетричному вигляді:

1) якщо функція f (x) парна (або задана на проміжку (0; ∞) і продовжена на всю числову пряму парним способом), то

			2			∞
		f (x) =		π		∫		F (ω) cos ωxdω,
						0			C
де
					2 ∞
	FC (ω) =						∫		f (t) cos ωtdt;
					π
						0
2) якщо функція f (x)		непарна (або задана на проміжку (0; ∞) і продо-
вжена на всю числову пряму непарним способом), то
			2 ∞
	f	(x) =	π ∫			F			(ω) sin ωxdω,
			0					S
102

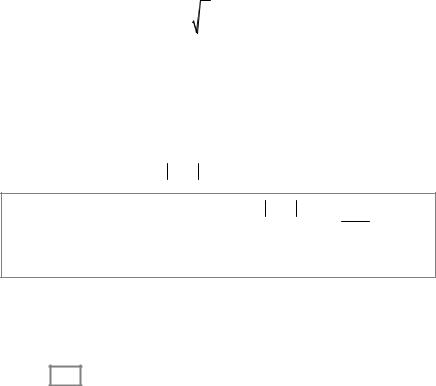
де

		2 ∞
	FS (ω) =		∫	f (t) sin ωtdt.
		π
		0
Функцію FC (ω) називають косинус-перетворенням Фур’є, а FS (ω) ―

синус-перетворенням Фур’є для функції f (x) .

Функції F(ω) , FC (ω) , FS (ω) називають також спектральною щільністю функції f (x).

Комплексну функцію F(ω) можна записати у вигляді

F(ω) = F(ω) eiϕ(ω) , − ∞ < ω < ∞ .

Модуль спектральної щільності A (ω) = F (ω) називають амплітуд-

ним спектром, а аргумент спряженої функції ϕ(ω) = arg F(ω) ― фазовим спектром функції f (x) . Вони визначають відповідно амплітуду і фазу коливання з частотою ω .

Перетворення Фур’є широко використовується для розв’язання багатьох практичних задач математичної фізики, електротехніки, цифрової обробки сигналів тощо.

Т.4 ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ

Подайте функцію f (x) у вигляді інтеграла Фур’є, знайдіть спектральну

щільність, амплітудний та фазовий частотні спектри. Побудуйте графіки функції f (x) , амплітудного та фазового частотних спектрів.

	e−2x , якщо x ≥ 0,
1.
	f (x) =
		0,	якщо x < 0.

Розв’язання. Графік функції f (x) зображено на рис. 1.12. Переконаємось спочатку, що ця функція абсолютно інтегровна:

∞

0

∞

e

−2x

A

1

∫

f (x)

dx = ∫

0 dx + ∫

e−2x dx = lim

=

< ∞ .

−2

2

−∞

−∞

−∞

A→∞

0

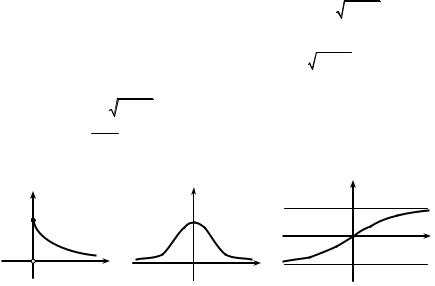
За формулою (1.47) знайдемо спектральну щільність

103

∞

∞

∞

F(ω) = ∫ f (t)e−iωt dt = ∫ e−2t e−iωt dt = ∫ e−(2+iω)t dt =

−∞

0

0

=

lim

e−(2+iω)t

A

=

1

=

2 − iω

.

4 + ω2

A→∞ −(2 + iω)

0

2

+ iω

Підставивши значення спектральної щільності у формулу (1.46), дістанемо розклад заданої функції в інтеграл Фур’є

1

∞

f (x) =

∫

2 − iω

eiωx dω.

2π

2

−∞ 4 + ω

Ця рівність справджується для всіх дійсних x, крім

x = 0 , для якого

має місце формула

1

∞

2 − iω

1

∫

eiωx dω =

.

2

2

2π −∞

4 + ω

Знайдемо амплітудний та фазовий частотні спектри:

F(ω) =

F(ω)

earg F (ω) ,

F(ω)

=

2 − iω

=

2 − iω

=

1

,

4 + ω2

4 + ω2

4 + ω2

ω

arg F(ω) = arctg −ω /(4 + ω2 ) = − arctg ω , F(ω) =

1

e−i arctg

2 ,

2 /(4 + ω2 )

2

4 + ω2

A(ω) =

F(ω)

=

1

— амплітудний частотний спектр (рис.1.13),

4 + ω2

ϕ(ω) = arg F(ω) = arctg ω2 — фазовий частотний спектр (рис.1.14)

f(x)			А(ω)		φ(ω)
					π/2
1			0,5
					О	ω
		х		ω
О			О		–π/2
Рис. 1.12			Рис. 1.13		Рис. 1.14

104

		sin	x, якщо | x | ≤ π,
	2. f (x) =
		0,	якщо | x | > 0.

Розв’язання. Задана функція абсолютно інтегровна, обмежена, куско- во-монотонна на кожному скінченному інтервалі (рис. 1.15). Отже, її

можна подати у вигляді інтеграла Фур’є. Оскільки функція f (x) непарна, то знаходимо її синус-перетворення Фур’є:

2 ∞

2

π

F

(ω) =

π ∫

f (t) sin ωtdt =

π

∫

sin t sin ωtdt =

S

0

0

1

2

π

(cos(1− ω)t − cos(1+ ω)t ) dt =

1 sin(1− ω)t

sin(1+ ω)t

π

=

∫

−

=

2

π

1− ω

1+ ω

0

2π

0

1

sin(1− ω)π

sin(1+ ω)π

1 sin ωπ

sin

ωπ

2 sin ωπ

=

−

=

+

=

,

2π

1

− ω

1

+ ω

1+ ω

π 1− ω

2

2π 1− ω

деω ≠ 1.

Для ω = 1 маємо

2

π

2

1

2

π

1

2

sin 2t

π

π

FS (1)

=

∫ sin

tdt =

∫ (1− cos 2t)dt =

t −

=

.

π

2

π

2

π

2

2

0

0

0

Крім того,

lim

F (ω) =

2

lim

sin ωπ

=

2

lim

π cos ωπ =

2

−π

=

π .

π

ω→1

S

ω→1 1− ω2

π ω→1

−2ω

π −2

2

Отже, синус-перетворення Фур’є

FS (ω) на проміжку [0; ∞) ― непе-

рервна функція (рис. 1.16).

FS(ω)

f(x)

π

1

1

1 − ω2

2

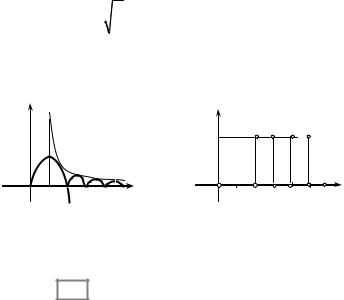
–π

О

π

х

1

2

3 4

ω

–1

О

Рис. 1.15

Рис. 1.16

Зображення функції f (x) інтегралом Фур’є має вигляд

105

2

∞ sin ωπ

f (x) =

∫

sin ωxd

ω .

π

2

0 1− ω

Ця рівність виконується для всіх значень х.

Знайдемо амплітудний та фазовий частотні спектри:

якщо

sin ωπ

> 0,

0,

2

A(ω) =

FS (ω)

2

sin ωπ

1

− ω

=

, ϕ(ω) =

sin ωπ

π

1− ω2

π, якщо

< 0.

2

1− ω

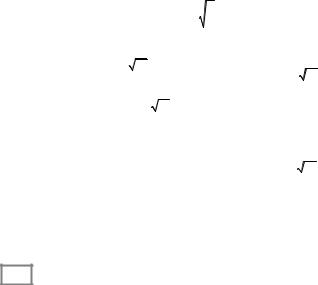
Будуємо графіки функцій A(ω),

ϕ(ω) (рис. 1.17 та 1.18).

А(ω)

φ(ω)

π

ω

О 1

3 4

ω

О

2

2 3 4 5

Рис. 1.17

Рис. 1.18

Т.4 ВПРАВИ ДЛЯ АУДИТОРНОЇ І САМОСТІЙНОЇ РОБОТИ

Подайте функцію f (x) у вигляді інтеграла Фур’є, знайдіть спектральну

щільність, амплітудний та фазовий частотні спектри. Побудуйте графіки функції f (x) , амплітудного та фазового частотних спектрів.

1.	x, якщо | x | ≤ 1,		2.	cos πx, якщо | x | ≤ 0, 5,
	f (x) =	якщо | x | > 1.		f (x) =
	0,			0, якщо | x | > 0, 5.
3. Знайдіть амплітудний та фазовий спектри функції
			1, якщо 1 ≤ x ≤ 2,
		f (x) =		якщо x < 1 або x > 2.
			0,

106

4. Знайдіть перетворення Фур’є функції

cos(x		/ 2),	якщо | x | ≤ π,
f (x) =	0,		якщо | x | > 0.

5.Зобразіть інтегралом Фур’є функцію

x, якщо 0 ≤ x < 1, f (x) = 1, якщо 1 ≤ x < 2,

0, якщо x ≥ 2.

Відповіді

4

∞ sin2 ω

2

2sin2 ω

1.

f (x) =

∫

2

cos ωxdω, x R,

FC (ω) = A(ω) =

2

,

ϕ(ω) = 0.

2.

f (x) =

π

2

π

2

0

ω

ω

ω

cos

ω

ω

∞

2

cos 2

2π

,

якщо ω ≠ π,

cos 2

2

2

= 2

∫

cos ωxdω,

x R, FC (ω) =

π

− ω

A(ω) = 2π

,

π2 − ω2

π2 − ω2

1

0

,

якщо ω = π,

8π

ω

cos 2

0, якщо

≥ 0,

π2

− ω2

2

ω

3ω

1

4 cos πω

3. A(ω)

4.

F(ω) =

ϕ(ω) =

=

sin

, ϕ(ω) =

.

.

ω

ω

2

2

2π

1 − 4ω2

cos 2

π, якщо

< 0.

π

2

− ω

2

∞

2

sin ω

cos 2ω

5.

∫

−

sin ωxdω.

π

2

ω

0

ω

Т.4 ІНДИВІДУАЛЬНІ ТЕСТОВІ ЗАВДАННЯ

Зобразіть інтегралом Фур’є функції

0, якщо x ≤ 0,

1.f (x) = sin x, якщо 0 < x < π,

0, якщо x ≥ π.

0, якщо x ≤ 0,

3.f (x) = cos, якщо 0 < x < π,

0, якщо x ≥ π.

f (x) .

		+ x, якщо − 1 < x < 0,
	1
2.		− x, якщо 0 ≤ x < 1,
	f (x) = 1
			0, якщо | x |≥ 1.
	0,		якщо x < −1,
4.			якщо − 1 ≤ x ≤ 0,
	f (x) = 1,
	0, якщо x > 0.

107

2, якщо 0 < x < 3, 5. f (x) = 1, якщо x = 3,

0, якщо x > 3.

0, якщо x < 0,

7.f (x) = 1− x, якщо 0 ≤ x ≤ 1,0, якщо x > 1.

0, якщо x < 0,

9. f (x) = x, якщо 0 ≤ x ≤ 1,0, якщо x > 1.

	4,	якщо 0 < x < 2,
6.		якщо x = 2,
	f (x) = 2,
		якщо x > 2.
	0,

0, якщо x < 0,

8.f (x) = πx, якщо 0 ≤ x ≤ 1,0, якщо x > 1.

6, якщо 0 < x < 4, 10. f (x) = 3, якщо x = 4,

0, якщо x > 4.

Знайдіть синус-перетворення Фур’є функції f (x) .

1, якщо 0 ≤ x ≤ 2,

11. f (x) =

0, якщо x > 2.

2, якщо 0 ≤ x ≤ 3,

13. f (x) =

0, якщо x > 3.

2x + 1, якщо 0 ≤ x ≤ 1,

15. f (x) =

0, якщо x > 1.

x, якщо 0 ≤ x ≤ 1,

12. f (x) =

0, якщо x > 1.

2x, якщо 0 ≤ x ≤ 1,

14. f (x) =

0, якщо x > 1.

x − 1, якщо 0 ≤ x ≤ 2,

16. f (x) =

0, якщо x > 2.

Знайдіть косинус-перетворення Фур’є функції f (x) .

		якщо 0 ≤ x ≤ 4,				x, якщо 0 ≤ x ≤ 1,
17.	1,			18.	f (x) =
	f (x) =	якщо x > 4.
	0,				0, якщо x > 1.
19.	2, якщо 0 ≤ x ≤ 2,			20.	x + 1, якщо 0 ≤ x ≤ 1,
	f (x) =	якщо x > 2.			f (x) =		0, якщо x > 1.
	0,
	sin x, якщо 0 ≤ x ≤ π,						− x	, якщо 0 ≤ x ≤ 1,
21.				22.	e
	f (x) =	якщо x > π.			f (x) =		0, якщо x > 1.
	0,
		1,	якщо 0 ≤ x ≤ 1,				2, якщо 0 ≤ x ≤ 1,
23.				24.			− x, якщо 1 < x < 3,
	f (x) = 2 − x, якщо 1 < x < 2,				f (x) = 3
		0,	якщо x ≥ 2.				0, якщо x ≥ 3.

108

Знайдіть амплітудний і фазовий спектри функції					f (x) .
	0, якщо x < 0,			0,	якщо x < 0,
25.		якщо 0 ≤ x ≤ 2,	26.		якщо 0 ≤ x ≤ 1,
	f (x) = 1,			f (x) = 2,
		якщо x > 2.			якщо x > 1.
	0,			0,
	0,	якщо x ≤ 1,		0,	якщо x < 1,
27.		якщо 1 < x ≤ 2,	28.		якщо 1 ≤ x ≤ 3,
	f (x) = 1,			f (x) = 2,
		якщо x > 2.			якщо x > 3.
	0,			0,
	0, якщо x < 2,			0, якщо x < 4,
29.		якщо 2 ≤ x ≤ 3,	30.		якщо 4 ≤ x ≤ 5,
	f (x) = 1,			f (x) = 3,
		якщо x > 3.			якщо x > 5.
	0,			0,

109

Модуль

2

КРАТНІ, КРИВОЛІНІЙНІ, ПОВЕРХНЕВІ ІНТЕГРАЛИ. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ

Загальна характеристика розділу. У розділі вивчаються подальші узагальнення поняття «Визначений інтеграл» на області інтегрування більш складного вигляду й іншої розмірності. Розглядаються застосування до задач геометрії, механіки та фізики.

СТРУКТУРА МОДУЛЯ

Тема 1. Подвійні інтеграли. Тема 2. Потрійні інтеграли. Тема 3. Криволінійні інтеграли. Тема 4. Поверхневі інтеграли. Тема 5. Елементи теорії поля.

Базисні поняття. 1. Інтегральна сума по плоскій і просторовій області. 2. Криволінійний і поверхневий інтеграли 1-го і 2-го роду. 3. Скалярне і векторне поля. 4. Похідна за напрямом. 5. Градієнт. 6. Оператор Гамільтона. 7. Дивергенція. 8. Ротор. 9. Потік векторного поля. 10. Циркуляція. 11. Потенціал.

Основні задачі. 1. Обчислення інтегралів. 2. Відшукання довжин, площ, об’ємів, мас тощо дуг, поверхонь плоских і просторових областей. 3. Визначення роботи силового поля. 4. Відшукання характеристик скалярного і векторного полів. 5. Визначення типу векторного поля (потенціальне, соленоїдальне, гармонічне) за його диференціальними характеристиками. 6. Відшукання інтегральних характеристик векторного поля (потік, робота, циркуляція, потенціал).

ЗНАННЯ ТА ВМІННЯ, ЯКИМИ ПОВИНЕН ВОЛОДІТИ СТУДЕНТ

1.Знання на рівні понять, означень, формулювань

1.1.Означення подвійного інтеграла, властивості, геометричний зміст, обчислення.

1.2.Заміна змінних у подвійному інтегралі. Перехід до полярних коор-

динат.

1.3.Застосування подвійного інтеграла.

110