0887579_C36AB_denisyuk_v_p_repeta_v_k_gaeva_k_a_kleshnya_n_o_visha_matemat

2. Обчисліть потрійний інтеграл

xdxdydz

∫∫∫G (1+ 2 y + z)3 ,

якщо область G обмежена площинами x = 0 , y = 0 , z = 0 , x + y + z = 1 .

Розв’язання. Область G — прямокутна трикутна піраміда, обмежена координатними площинами і похилою площиною x + y + z = 1 (рис. 2.32).

Ця область правильна у напрямку будь-якої осі координат. Розставимо межі інтегрування у потрійному інтегралі. Спроектуємо область G на площину Оху, дістанемо область D ― трикутник ОАВ (рис. 2.33), межі якого визначаються рівняннями x = 0 , y = 0 , x + y = 1 (у площині Оху

z = 0 ). Для точок області D змінна х змінюється від нуля до одиниці, тобто x [0; 1] . Для будь-якого фіксованого х із цього проміжку у змінювати-

меться так: 0 ≤ y ≤ 1− x . Нарешті, для будь-яких фіксованих х та у з області

D змінна z набиратиме значень від z1 = 0 до																																																z2					= 1− x − y , тобто z зміню-
ється від нижньої межі ― площини																																				z = 0										до верхньої межі ― площини
x + y + z = 1. Далі маємо
														xdxdydz										1							1− x									1− x− y														dz
										∫∫∫												=∫ xdx ∫														dy								∫																		=
												(1+ 2 y + z)								3																												(1+ 2 y + z)											3
										G														0						0													0
	1			1− x						1									1− x− y																	1	1								1− x											1											1
=	∫	xdx			∫																	dy						= −									∫			xdx						∫																		−								dy =
																2																																													2										2
							−2(1			+ 2 y + z)																										2															(2 − x + y)														(1+ 2y)
	0				0														0																		0									0
			1		1					1									1								1− x																1			1										1						1						1
	= −				∫ x		−								+																dx = −															∫ x														−							−		dx =
			2						2	− x + y						2(1+ 2 y)																											2									2(2x − 3)												x − 2				2
					0																						0																			0
						1	1	1							3										2											x													1							3				3
			= −				∫			1	+								− 1		−										−						dx = −																	−				x +						ln		2x − 3				−
						2	0		4					2x − 3										x	−			2								2													2							4				8
																	x − 2							x2							1						1																3
													−2 ln								−															=						− ln 2 +														ln 3.
																								4							0						2																16
		z																														z																															у
			1																											1
																																																																1 В
		1 О													4				у																													В																			x + y =1
																															О																							у																	А
3																																															1
																									А																																							О							1	х
																												1
	x																					х
				Рис. 2.31																										Рис. 2.32																																				Рис. 2.33
																																																																								151

3. Обчисліть потрійний інтеграл

yz

∫∫∫G 1− x2 dxdydz,

де область G обмежена поверхнями z = 1− x2 , x + y − 2 = 0 , y = 0 , z = 0 . Розв’язання. Побудуємо область G. Поверхня z = 1− x2 є параболіч-ний циліндр, напрямна якого ― парабола z = 1− x2, розміщена у площині Oxz, а твірні паралельні осі Oу. Циліндр перетинає площину Oxу (z = 0) по

прямих x = 1 та x = −1 . Площина x + y − 2 = 0	паралельна осі	Oz і пере-
тинає площину Oxу по прямій x + y − 2 = 0 .	Побудувавши перетин цих
поверхонь, дістанемо область G (рис. 2.34). Проекція області		G на пло-

щину Oxу (область D) має форму трапеції. При обчисленні подвійного інтеграла по області D доцільно використати формулу (2.4). При такому виборі порядку інтегрування х змінюється від –1 до 1, а у ― від прямої

y = 0					(вісь Ох) до прямої										y = 2 − x .				При обранні іншого порядку інте-
грування область D необхідно розбити на дві частини.
Отже, за формулою (2.18) маємо
							yz	1			dx				2− x	1− x2								1		dx				2− x		z2				1− x2
∫∫∫									dxdydz = ∫						∫	ydy ∫				zdz = ∫										∫	y							dy =
					1		− x	2			− x		2													− x		2				2
	G								−1 1					0			0							−1 1					0							0
	1				1				2− x			1		1					y	2			2− x				1		1
=					∫ (1− x2 )dx ∫ ydy =									∫ (1− x2 )										dx =					∫ (1− x2 )(2 − x)2 dx =
																		2
2				−1				0			2		−1										0			4		−1
	1				1		(4	− 4x − 3x2 + 4x3 − x4 )dx =									1																x5					1
						∫														4x − 2x2 − x3									+ x4 −
=	4																4															5						= 1, 4.
					−1																																	−1

4.Обчисліть потрійний інтеграл

∫∫∫(x2 + y2 )dxdydz ,

G

якщо область G обмежена площиною z = 3 і круговим параболоїдом x2 + y2 = 3z .

Розв’язання. Область інтегрування G (рис. 2.35) обмежена знизу параболоїдом x2 + y2 = 3z , а зверху ― площиною z = 3 . Проекція цієї області

на площину Оху ― круг, обмежений колом x2 + y2

результатом виключення змінної z із системи рівнянь x2 Введемо циліндричні координати

x = ρ cos ϕ , y = ρ sin ϕ , z = z .

152

=9 (це рівняння є

+y2 = 3z та z = 3 ).

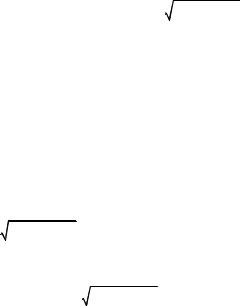
Рівняння параболоїда набирає вигляду z = ρ2 , а рівняння площини не

3

змінюється. Визначаємо межі зміни циліндричних координат в області G:

0 ≤ ϕ ≤ 2π , 0 ≤ ρ ≤ 3 , ρ2 ≤ z ≤ 3 . 3

Тепер обчислюємо потрійний інтеграл

												2π				3			3							2π		3						3
	∫∫∫ (x2 + y2 )dxdydz = ∫															dϕ∫ dρ ∫						ρ2 ρdz = ∫ dϕ∫ ρ3 z												ρ	2	dρ =
		G											0			0				ρ2						0		0
																																		3
																			3
2π			3					ρ2				2π					3						ρ5			2π 3ρ4								ρ6				3
∫			∫	3									∫				∫		3								∫
= dϕ ρ						3 −				dρ =						dϕ		3ρ −						dρ =							−							dϕ =
0			0					3					0				0						3				0	4					18					0
							2π	35			35				3				243			2π			81				81π
							∫									dϕ =						∫	dϕ =			2π =
					=					−	6								12						4				2				.
							0 4								0							0

5.Обчисліть потрійний інтеграл

∫∫∫x2 + y2 + z2 dxdydz ,

G

якщо область G обмежена сферою x2 + y2 + z2 = 2z .

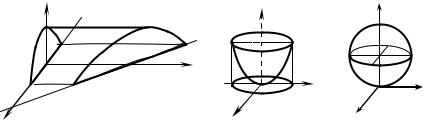
Розв’язання. Виділивши повний квадрат за змінною z, запишемо рівняння сфери у вигляді x2 + y2 + (z − 1)2 = 1 . Отже, центр сфери лежить у

точці (0; 0; 1), а радіус дорівнює одиниці (див. рис. 2.36). Форма області G , а також вираз підінтегральної функції вказують на доцільність проведення обчислення потрійного інтеграла у сферичній системі координат. Врахову-

ючи, що у сферичних координатах			x2 + y2 + z2 = r2 , рівняння		сфери
набере вигляду	r2 = 2r cos θ , або	r = 2cos θ . Визначаємо межі зміни сфе-
ричних координат: 0 ≤ ϕ ≤ 2π ,		0 ≤ θ ≤ π ,		0 ≤ r ≤ 2 cos θ . Крім	того,
			2
x2 + y2 + z2 = r , J = r2 sin θ .
Використовуючи формулу (2.21), дістанемо
			π
∫∫∫		2π	2	2 cos θ
	x2 + y2 + z2 dxdydz = ∫		dϕ∫ dθ	∫ r r2 sin θdr =
V		0	0	0
					153

π

π

π

2π

2

2 cos θ

2π

2

r

4

2 cos θ

2π

2

= ∫

dϕ∫ sin θdθ ∫

r3 dr = ∫

dϕ∫ sin θ

dθ = ∫

dϕ∫ 4 cos4 θ sin θdθ =

0

0

0

0

0

4

0

0

0

2π

π

2π

π

2π

2

4

4

8π

= −4 ∫

dϕ∫ cos4 θd(cos θ) = −

∫ cos5

θ

2

dϕ =

∫

dϕ =

4

2π =

.

0

0

5

0

0

5

0

5

5

z

z = 1 – х2

z

z

–1

G

2

3

1

1

О

D

2

y

2

–3

3

3

y

О

у

x

х

x

Рис. 2.34

Рис. 2.35

Рис. 2.36

6. Обчисліть об’єм тіла, обмеженого поверхнями

y = x, x + y − 4 = 0, x + z − 2 = 0, x = 0, z = 0 .

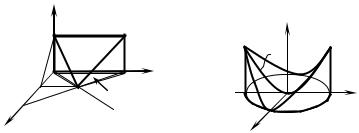
Розв’язання. Побудуємо задане тіло.

Площина

y = x проходить через

вісь Oz і перетинає площину Оху по прямій

y = x . Площина

x + y − 4 = 0

паралельна осі Oz і перетинається з площиною Оху по прямій x + y − 4 = 0 ,

а площина x + z − 2 = 0 паралельна осі Oу і перетинає площину Oхz по прямій x + z − 2 = 0 . Побудувавши перетин цих поверхонь, дістанемо тіло G (рис. 2.37), проекцією якого на площину Оху є область D — трикутник OMK. Прямі x + y = 4 та y = x перетинаються в точці M (2; 2) , отже, область

D проектується на вісь Ох у відрізок [0; 2], тобто х змінюється від 0 до 2, у ― від прямої y = x до прямої y = 4 − x , а z ― від площини z = 0 до площини

z = 2 − x . Для обчислення об’єму використовуємо формулу (2.18):

		2		4− x			2− x			2	4− x					2− x		2	4− x
V = ∫∫∫ dxdydz = ∫ dx ∫					dy ∫			dz = ∫ dx ∫							z		dy = ∫		(2 − x)dx ∫ dy =
G		0		x			0			0	x					0		0	x
2	(2 − x) y		4−x			2											2	(4 − 4x + x2 )dx =
= ∫				dx	=∫ (2 − x)(4 − 2x)dx = 2∫
0			x			0											0
							4x − 2x		2		x3				2		16
				=	2					+					=			.
											3				0		3

154

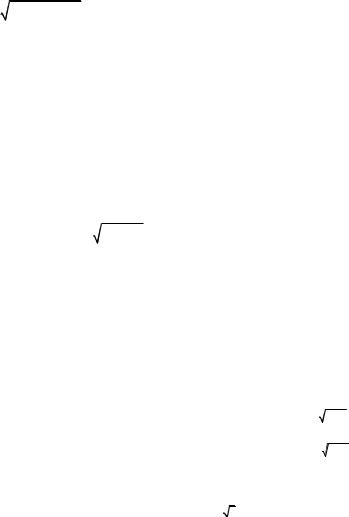
7. Обчислітьоб’ємтіла, обмеженого поверхнями x2 + y2 = 4,		z = y2 ,	z = 0.
Розв’язання. Побудуємо тіло. Поверхня	x2 + y2 = 4 ― нескінченний
круговий циліндр, що перетинає площину	Оху по колу	x2 + y2	= 4 з

центром у початку координат і радіусом R = 2 , його твірні паралельні осі Oz. Поверхня z = y2 ― нескінченний параболічний циліндр, що перети-

нає площину Oyz по параболі z = y2 , його твірні паралельні осі Ox. Пло-

щина z = 0 ― координатна площина Oxy. Утворене тіло (рис. 2.38) проектується на площину Oxy у круг D. Тому обчислення проведемо у циліндричних координатах. Оскільки полюс О міститься всередині області D, то при розстановці меж у подвійному інтегралі використаємо формулу (2.10).

Введемо циліндричні координати за формулами x = ρ cos ϕ , y = ρ sin ϕ , z = z.

Рівняння параболічного циліндра набирає вигляду z = ρ2 sin2 ϕ , а рів-

няння кола x2 + y2 = 4 спрощується до вигляду ρ = 2 . Визначаємо межі зміни циліндричних координат в області G:

0 ≤ ϕ ≤ 2π , 0 ≤ ρ ≤ 2 , 0 ≤ z ≤ ρ2 sin2 ϕ .

Тепер обчислюємо об’єм заданого тіла

V = ∫∫∫ dxdydz = ∫∫ ρdρdϕ			ρ2 sin2 ϕ							2π	2				ρ	2	sin	2	ϕ ρdρ =
			∫			dz = ∫ dϕ∫ z
G	D		0						0		0				0
2π	2	2π				ρ	4			2			2π
= ∫ sin2 ϕdϕ∫ ρ3 dρ = ∫ sin2 ϕ										dϕ = 4 ∫ sin2 ϕdϕ =
0	0	0				4				0	0
= 22π	1− cos 2ϕ dϕ = 2				ϕ −			sin 2ϕ					2π		= 4π.
∫	(	)							2
0													0

z
2	z

x + z = 2		O	K	z = y2
					G
				y
	2		4
4		М	D	D	2	y
	x + y = 4

x	x = y	x
Рис. 2.37		Рис. 2.38

155

Т.2 ВПРАВИ ДЛЯ АУДИТОРНОЇ І САМОСТІЙНОЇ РОБОТИ

Розставте межі інтегрування у потрійному інтегралі ∫∫∫ f (x,									y, z)dV по
області G, обмеженій поверхнями:								G
1.	x = 0 , y = 0 , z = 0 , 3x + 6 y + 4z − 24 = 0 .
2.	x = 0 , y = 0 , x = 2 , y = 3 , z = 0 , z = 3 − y .
3.	x2 + y2 = 4 , z = −1 , z = 4 .
Обчисліть інтеграли.
	1	1	2		1	1− x	1− x− y	dz
4. ∫ dx∫ dy∫				(x + 2 y + 4z)dz .	5. ∫ dx ∫		dy ∫				.
								(3x + 2 y + z − 4)		4
	0	0	0		0	0	0
	1	2− y		1
6.	∫ dy ∫		dx∫ (x2 + y)zdz .
	0	y2		0

Обчисліть потрійні інтеграли в декартовій системі координат.

7.	∫∫∫ x2 yzdxdydz , якщо область G обмежена площинами	x = 0 ,	y = 0 ,
	G
z = 0 та x + y + z = 2 .
8.	∫∫∫ (x + y + z)dxdydz, область G обмежена площинами	x = 0 ,	y = 0 ,
	G
z = 0 , x = 1, y = 1 , z = 1 .
9.	∫∫∫ x2 dxdydz , якщо область G обмежена циліндром	x2 + y2	= 1 та
	G
площинами z = 0 і z = 3.

Обчисліть потрійні інтеграли, використавши перехід до циліндричних координат.

10. ∫∫∫ (x2 + y2 + z2 )dxdydz, якщо область G обмежена круговим ци-

G

ліндром x2 + y2 = 4 та площинами z = 0 , z = 1 .

11. ∫∫∫ zdxdydz , якщо область G обмежена конусом z2 = x2 + y2 та

G

площиною z = 2 .

156

12. ∫∫∫ (x + y2 + z2 )3 dxdydz , якщо область G обмежена параболоїдом

G

x = y2 + z2 та площиною x = 1 .

Обчисліть потрійні інтеграли, використавши перехід до сферичних координат.

13. ∫∫∫ x2 + y2 + z2 dxdydz , якщо область G обмежена сферою

G

x2 + y2 + z2 = y.

14. ∫∫∫ (x2 + y2 )dxdydz , якщо область G визначається нерівностями

G

z ≥ 0 та x2 + y2 + z2 ≤ 1.

15. ∫∫∫ (x2 + y2 + z2 )2 dxdydz , якщо G — куля x2 + y2 + z2 ≤ R2 .

G

Обчисліть об’єм тіла, обмеженого поверхнями.

16.	z = 4	− x2 ,	z = x2 + 2,	y = −1, y = 2.
17.	z = x2 + y2 ,		z = 1.
18.	z = 2	− x2 − y2 , z =		x2 + y2	(конус).
19.	x2 + y2 + z2		= 4, x2 + y2 + z2		= 9, z2 = x2 + y2 , z ≥ 0 .

Обчисліть масу тіла, обмеженого заданими поверхнями з густиною

γ(x, y, z) .

20.z = x2 + y2 , z = 4 , γ(x, y, z) = (x2 + y2 + z)2 .

21.x2 + y2 + z2 = R2 , γ(x, y, z) = (x2 + y2 + z2 )3 .

Відповіді

	4−	x		24−3x−6 y
8		2		4
1. ∫dx ∫			dy	∫
0	0			0

4

× ∫ f (x, y, z)dz. 4. 11.

−1

							2		3	3+ y									2	4− x2
f (x, y, z)dz.						2. ∫dx∫dy ∫ f (x, y, z)dz.											3. ∫ dx ∫ dy ×
							0		0	0									−2	− 4− x2
5.		1	. 6.	27	.	7.		16	. 8.		3	.	9.	3	π.	10.	28π	.	11. 4π . 12.		π .
	144			42			315			2				4			3				2

	13.		π	. 14.		4	π. 15.	4πR7	. 16. 8.	17.	π	. 18.	5π	. 19.	19(2 − 2)π		. 20.	448π	. 21.	4πR9	.
		10			15			7			2		6		3			3		9

157

Т.2 ІНДИВІДУАЛЬНІ ТЕСТОВІ ЗАВДАННЯ

2.1. Обчисліть потрійний інтеграл ∫∫∫ f (x, y, z)dxdydz. Пiдiнтегральна

V

функція f(x, у, z) та поверхнi, що обмежують область V, вказанi в таблицi 1.

Таблиця 1

№	f(x, у, z)	Область V
1	5y – 4	x = 0, y = 0, z = 0, x + y + 2z – 6 = 0.
2	6y + 2z	x = 0, y = 0, z = 0, 3x + y + z – 9 = 0.
3	5 + y + 2х	x = 0, y = 0, z = 0, 2x + 3y + z – 2 = 0.
4	4x – y	x = 0, y = 0, z = 0, 4x + y + 2z – 1 = 0.
5	3 + 4z	x = 0, y = 0, z = 0, x + 4y + z – 4 = 0.
6	7y – 2z	x = 0, y = 0, z = 0, 3x + y + 3z – 6 = 0.
7	xy + 1	x = 0, y = 0, z = 0, 6x + 2y +z – 8 = 0.
8	3y – 2 z	x = 0, y = 0, z = 0, 7x + y + z – 3 = 0.
9	2x + z	x = 0, y = 0, z = 0, 4x + 2y + 4z – 1 = 0.
10	3 + 4z	x = 0, y = 0, z = 0, 8x + 2y + 2z – 3 = 0.
11	4y + 5	x = 0, y = 0, z = 0, 3x + y + z – 6 = 0.
12	3x + 2	x = 0, y = 0, z = 0, 7x + y + 7z – 14 = 0.
13	3xy	x = 0, y = 0, z = 0, 2x + 4y + z – 8 = 0.
14	8y – 2z	x = 0, y = 0, z = 0, 5x + y + 10z – 10 = 0.
15	5x + z	x = 0, y = 0, z = 0, 3x + 2y + 6z – 6 = 0.
16	7 – 4z	x = 0, y = 0, z = 0, 4x + y + 2z – 8 = 0.
17	3x + 2y	x = 0, y = 0, z = 0, 6x + 3y + z – 18 = 0.
18	3xy + 2	x = 0, y = 0, z = 0, 5x + 15y + z – 15 = 0.
19	6z + 3	x = 0, y = 0, z = 0, 2x + y + 5z – 10 = 0.
20	4x + y	x = 0, y = 0, z = 0, 3x + 4y + z – 12 = 0.
21	xy	x = 0, y = 0, z = 0, 4x + 2y + 3z – 12 = 0.
22	5 – 8z	x = 0, y = 0, z = 0, 5x + 3y + 15z – 15 = 0.
23	y + 2	x = 0, y = 0, z = 0, x + 5y + 3z – 15 = 0.
24	y – 6z	x = 0, y = 0, z = 0, 2x + 5y + z – 10 = 0.
25	2x – y	x = 0, y = 0, z = 0, 3x + 6y + 2z – 12 = 0.

158

Закінчення табл. 1

№	f(x, у, z)	Область V
26	3 – 2z	x = 0, y = 0, z = 0, x + 2y + 4z – 8 = 0.
27	х + 3y	x = 0, y = 0, z = 0, 8x + y + 2z – 8 = 0.
28	2z + 1	x = 0, y = 0, z = 0, 4x + 6y + 3z – 12 = 0.
29	2x + y	x = 0, y = 0, z = 0, 2x + 9y + 2z – 18 = 0.
30	у + 4z	x = 0, y = 0, z = 0, x + 5y + 4z – 20 = 0.

2.2. Знайдіть об’єм тіла, обмеженого вказаними поверхнями. Обчислення проведіть у циліндричній або сферичній системі координат.

2.2.1. x2 + y2 + z2			= 1, x2 + y2 + z2 = 9 ,			z =	x2 + y2	(конус).
2.2.2. x2 + y2 + z2			= 4 ,	x2 + y2 + z2 = 9 ,		z =	x2 + y2	( x ≥ 0 , y ≥ 0 ).
2.2.3. x2	+ y2	+ z2	= 4 ,	z =	x2 + y2 .
2.2.4. x2	+ y2	+ z2	= 16 ,	y =	x2 + z2 .
2.2.5. x2	+ y2	+ z2	= 4 ,	z =	3(x2 + y2 ) .
2.2.6. x2	+ y2	+ z2	= 4 ,	3z = x2 + y2 .

2.2.7.z = x2 + y2 , z = 8 − x2 − y2 (круговий параболоїд).

2.2.8.x = y2 + z2 , x = 18 − y2 − z2 .

2.2.9.z = 2(x2 + y2 ) , z = 12 − x2 − y2 .

2.2.10.2z = x2 + y2 , z = 6 − x2 − y2 .

2.2.11.z = x2 + y2 , z = 16 − 3(x2 + y2 ) .

2.2.12.y = x2 + z2 , y = 3 − 2(x2 + z2 ) .

2.2.13.	z = 3	x2 + y2 ,		z =		5 − 2(x2 + y2 ) .
2.2.14.	x =	y2 + z2 ,		3x =		18 − y2 − z2 .
2.2.15.	z = 6 −		x2 + y2 ,		z = x2 + y2 .
2.2.16.	y = 4 − 3		x2 + z2		(конус), y = x2 + z2 .
2.2.17.	x2 + y2 + z2 = 1,				x2 + y2 + z2 = 16 , z = x2 + y2 ( x ≥ 0 ).

159

2.2.18.	x2	+ y2	+ z2	= 9 ,	x2	+ y2		+ z2	= 25 ,	z = 3(x2 + y2 ) .
2.2.19.	x2	+ y2	+ z2	= 4 ,	x2	+ y	2	+ z2	= 25 ,	3y = x2 + z2 .
2.2.20.	x2	+ y2	+ z2	= 4 ,	3y =			x2 + z2 .

2.2.21.x2 + y2 = 4 , z = 1 , z = x + 2 y + 6 .

2.2.22.x2 + y2 = 9 , z = x2 + y2 + 4 , z = 0 .

2.2.23.x2 + z2 = 1 , y = −1 , y = 10 − x2 − z2 .

2.2.24.x2 + y2 = 2x , z = 0 , z = x + y + 5 .

2.2.25.x2 + y2 = 4 y , z = 0 , z = 2x + y + 6 .

2.2.26.	z =	25 − x2 − y2	(í àï ³âñô åðà),		y = − x, y = 3x ( y ≥ 0).
2.2.27.	z =	16 − x2 − y2 ,	3x − y = 0,		x − 3y = 0 (x ≥ 0, y ≥ 0).
2.2.28.	z =	4 − x2 − y2 ,	y = x, y = 0 (x ≥ 0, y ≥ 0).
2.2.29.	z =	9 − x2 − y2 ,	3x − y = 0,	y = x (x ≥ 0, y ≥ 0).
2.2.30.	x2 + y2 + z2 = 4 ,		x2 + y2 + z2	= 4z (сфера).

Тема 3. КРИВОЛІНІЙНІ ІНТЕГРАЛИ

Криволінійні інтеграли першого та другого роду. Властивості та обчислення. Формула Гріна. Умови незалежності криволінійного інтеграла від форми шляху інтегрування. Інтегрування повних диференціалів. Застосування.

Література: [3, розділ 2, п. 2.4], [9, розділ 10, §3], [15, розділ 12, п. 12.3], [16, розділ 15, §1–4], [17, розділ 3, §9–10].

Т.3 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

3.1. Криволінійні інтеграли першого роду. Основні поняття

Криволінійний інтеграл є узагальненням визначеного інтеграла на випадок, коли областю інтегрування є деяка крива.

Нехай у площині Оху задано гладку або кусково-гладку криву L, обмежену точками А і В (рис. 2.39), і на цій кривій визначено неперервну

160