Матан_ЛинПрог

3.9. f x1 3x2 max 3.10. f 2x1 x2 min

								10x1 3x2 30 0														x1 2x2 2
								x x				2			5 0							2x x							2	0
								1																1
																								2x2 0
								x1 x2 10 0														x1
								x 2x 0														x x					2		1
								1					1									1
																x2 2							, x2 0
								x1 0,														x1
3.11. f				x1 2x2							max 3.12.							f x1 3x2 min											3.13. f						2x1 x2 max
x1 x2 1																	x1 2x2 2 0															x1 x2 1
2x x							2	2									x 2x			2		3 0										x x				2	3
		1															1																	1
		x2 4																2x2				6 0													x2 8
x1																	x1															x1
x 3																	x x		2		0											2 x 5
1																	1																		1
		, x2			0													, x2 0
x1																	x1															1 x2 4
							3.14. f					x1					x2 min					3.15. f			x1 2x2										max
								x1 x2 6														x1 2x1 4 0
								x 2x						2		0						x 2x								2	4 0
								1															1
								1 x1 3														x1 2x2 6 0
								x	2	0												x ,		x		2		0
																						1
3.16. f				x1 x2 min													3.17. f	3x1				4x2 max								3.18. f					2x1 x2 min
x1 2x2 4 0																	3x1 2x2 6 0														x1 2x2 4 0
2x x					2	4 0
		1																2x2				7 0												x2 3 0
x1 x2 4 0																	3x1														x1
x x			2	6 0													2x1	4x2				8 0									x1			x2 7 0
	1																x 1 0														x 2 0
x		4 0															1																1
	1																																	,	x2 0
																	x2 0														x1
		, x2			0
x1
							3.19. f					x1					7x2 max					3.20. f				2x1 6x2 min
								x1 x2 4 0														x1 x2 4 0
								x x					2			2 0						2x 6x										2	12 0
									1																	1
								x 1 0														x 2 0
									1														1
								x ,			x		2			0						x		2	0
									1

§4. Симплексный метод решения задач линейного программирования

Симплексный метод позволяет, исходя из известного опорного плана задачи, за конечное число шагов получить ее оптимальный план. Каждый из шагов (или итераций) состоит в нахождении нового плана, которому соответствует большее (или меньшее) значение линейной функции, чем в предыдущем плане. Если задача не обладает планами или ее линейная функция не ограничена на многограннике решении, то симплексный метод позволяет установить это в процессе решения.

Пусть дана задача линейного программирования:

Fmax c1x1 c2x2 ... cnxn cn 1xn 1 ... cn mxn m

при

a11x1 a12x2 ...

a1nxn xn 1 b1

21x1 a22x2

a2nxn xn 2 b2

a

.............................................

a

x a

m2

x

2

...

a

mn

x

n

x

n m

b

m1 1

m

(4.1)

(4.2)

xj 0

( j 1,n m)

(4.3)

Запишем систему (4.2) в векторной форме:

A1x1 A2x2 ... Anxn An 1xn 1 An 2xn 2 ... An mxn m B, (4.4)

где

		a				a				a				1					0			0
			11				12				1n
А1		a21				a22				a2n				0				1				0
			...	,А2			...	,...,Аn			...	,Аn 1				,Аn 2				,...,Аn m				,B
															...				...				...
															0				0
		am1				am2				amn												1

b1

b2

...bm

Векторы An 1, An 2,...,An m - линейно независимые единичные векторы m-мерного пространства. Они образуют базис пространства. Поэтому в разложении (4.4) за базисные неизвестные выбираем хn 1,хn 2,...,хn m, а

свободные неизвестные х1,х2,...,хn						приравниваем нулю и, учитывая, что
bi 0	(i			), а	векторы An 1	, An 2,...,An m - единичные,	получаем
		1,m
первоначальный план:
	X0 (x1		0;x2		0;...;xn 0;xn 1 b1;xn 2 b2;...;xn m bm)		(4.5)
Плану (4.5) соответствует разложение:
	An 1xn 1		An 2xn 2 ... An mxn m B				(4.6)
где	векторы			An 1, An 2,...,An m		линейно независимы, следовательно,
построенный первоначальный план (4.5) является опорным.

Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условие задачи и

первоначальные данные записать в симплекс-таблицу.
В столбец	«Базис» включают	единичные	(базисные) векторы
An 1, An 2,...,An m.	В столбце С	записывают	коэффициенты при

неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.

В столбце В записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана.

Столбцы векторов Аj представляют собой коэффициенты разложения

этих векторов по векторам данного базиса.

В симплекс-таблице первые m строк определяются исходными данными задачи, а показатели m 1 -ой строки вычисляют. В этой строке в столбце В записывают значение целевой функции, которое вычисляется по формуле:

F (C ,B)					(4.7)
а в столбце вектора Аj - значение:
j (C ,Aj ) cj , ( j			)		(4.8)
		1,n
m				m
где (C ,B) cibi	и	(C ,Aj		) ciaij ,	( j	1,n	), - скалярные
i 1				i 1

произведения векторов, а ci - элемент, стоящий в i-ой строке таблицы. Значения j называются оценками плана.

№	Бази	Сδ	В	c1	c2	…	cn	cn+1	cn+2	…	cn+m
	с			А1	А2	…	Аn	Аn+1	Аn+2	…	Аn+m
1	Аn+1	cn+1	b1	a11	a12	…	a1n	1	0	…	0
2	Аn+2	cn+2	b2	a21	a22	…	a2n	0	1	…	0
…	…	…	…	…	…	…	…	…	…	…	…
m	Аn+m	cn+m	bm	am1	am2	…	amn	0	0	…	1
m+1	j		F0	1	2	…	n	0	0	…	0

После заполнения таблицы исходный опорный план проверяют на оптимальность, просматривая элементы j m 1 -ой строки.

В результате может иметь место один из следующих трех случаев:

1) j 0 для всех j 1,n. Опорный план является оптимальным.

2) j	0 для	некоторого j, и			все соответствующие этому индексу
величины	aij 0	(i		). Целевая	функция не ограничена сверху на
			1,m

множестве планов и задача не имеет решения.

3) j 0 для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел aij положительно. Можно перейти от исходного плана к

новому опорному плану, при котором значение целевой функции увеличивается.

Этот переход от одного опорного плана к другому осуществляется исключением из базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять вектор Aj , для

которого отрицательное число j является наибольшей по абсолютной

величине. Для определения вектора, подлежащего исключению из базиса, находят число:

b
min		i		, где	aij 0	(4.9)
a
		ij

Выбранные таким образом столбец и строка называются направляющими, а стоящий на их пересечении элемент aij называется

разрешающим.

Элементы новой симплекс-таблицы находят с помощью метода ЖорданаГаусса.

Итак, переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой (от одной итерации к следующей итерации).

После заполнения m 1 -ой строки выясняют, является ли новый опорный план оптимальным. Если нет, то итерационный процесс продолжают до тех пор, пока либо не получат оптимальный план задачи, либо не установят ее неразрешимость.

Алгоритм решения задач симплексным методом

1.Находят опорный план.

2.Составляют симплекс-таблицу.

3.Выясняют, имеется ли хотя бы одно отрицательное число j . Если нет,

то найденный опорный план оптимален. Если же среди чисел j

имеются отрицательные, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану.

4.Находят направляющие столбец и строку. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом j , а направляющая строка – минимальным из отношений компонент столбца вектора В к положительным компонентам направляющего столбца.

5.Составляют новую таблицу и проверяют найденный опорный план на оптимальность. Если план не оптимален, то возвращаются к этапу 4, а в случае получения оптимального плана или установления неразрешимости процесс решения задачи заканчивают.

Задача. Решить симплексным методом задачу использования сырья из

§1.

		2x1			3x2			21
		x		x		2	8
Найти fmax 30x1 20x2	при		1
		2x			10
			1
		x		0,			x	2	0
			1

Решение. Приведем систему неравенств к канонической форме путем прибавления к левым частям неотрицательные переменные x3,x4,x5. Тогда получим:

fmax 20x1 20x2 0 x3 0 x4 0 x5

	2x1 3x2 x3 21
	x		x				2	x			4		8
при		1
	2x			x				5		10
		1
	x ,x				2	,x			3	,x		4	,x	5	0
		1
Экономический смысл	дополнительных													переменных: x3,x4,x5 -

неизрасходованное количество сырья S1,S2,S3 соответственно. Запишем полученную систему в векторной форме

А1x1 А2x2 А3x3 А4x4 А5x5 В,

где	2		3	1			0	0		21
А1 1 , А2 1 , А3 0 , А4 1 , А5 0 , В 8											.
	2		0	0			0	1		10

Единичные

векторы

А3,А4,А5

выберем за базис опорного плана,

свободные неизвестные

x3

,x4,x5 приравниваем нулю. То

есть,

пока

не

производятся изделия

P1

и

P2, в результате чего получим первоначальный

план X0 (x1

0;x2

0;x3

21;x4

8;x5 10). Сырье не

расходуется

и

прибыль

f0 0.

X0

Для

проверки плана

составляем

первую

симплекс-таблицу

(I

итерация)

и

подсчитываем

значение

f (X0) C В

и

оценок

j C

Аj

Cj. Если в таблице в

(m 1)-й строке все оценки j 0, то

полученный

план

X0

является

оптимальным;

если

же

имеются

отрицательные оценки, то отыскивается следующий опорный план. Процесс продолжают либо до получения оптимального плана, либо до установления неограниченности линейной функции.

В данной задаче имеем:

f (X0) 0 21 0 8 0 10 0, 1 C А1 C1 0 2 0 1 0 2 30 30,2 C А2 C2 0 3 0 1 0 0 20 20, 3 4 5 0.

	№	Баз	C	В
		ис
I	1	А3	0	21
	2	А4	0	8
	3
		А5	0	10

30	20	0	0	0
					b
А1	А2	А3	А4	А5	min	i
					a
						ij
2	3	1	0	0	21:2=10,5
1	1	0	1	0	8:1=8
2	0	0	0	1	10:2=5

	m 1		j				f0 0			-30		-20			0		0		0		X0=(0;0;21;8;10)
										↑
I	1		А3		0		11		0			3			1		0		-1		11:3=11/3
I	2		А4		0		3			0			1		0		1		-1/2		3:1=3
	3		А1		30		5		1			0			0		0		1/2		------
	m 1			j			f 150		0				-20		0		0		15		X1=(5;0;11;3;0)
							1						↑
I	1		А3		0		2		0			0			1		-1/3		1/2
II	2		А2		20		3		0			1			0		1		-1/2
	3		А1		30		5		1			0			0		0		1/2
	m 1		j				f2 21		0			0			0		0		5		Х*=(5;3;2;0;0)

Для векторов базиса оценки равны нулю. Среди полученных оценок j

есть отрицательные. Это означает, что первоначальный опорный план не является оптимальным и его можно улучшить, включив в базис вектор, которому соответствует наибольшая по модулю из отрицательных оценок. То есть вектор А1 - направляющий вектор-столбец, т.к. max{| 30|, | 20|} 30. Выпуск одной единицы продукции P1 приносит 30 денежных единиц, что приносит наибольшую прибыль, чем выпуск продукции P2. Т.е. начинаем производство продукции вида P1.

При нахождении по формуле (4.9) элементы столбца В делим соответственно на элементы направляющего столбца, но только на положительные элементы. Если среди элементов направляющего столбца не окажется хотя бы одно положительное число, то задача является неразрешимой.

Найдем min{21/2,8/1,10/2} 10/2 5. Разрешающим элементом будет число 2, а направляющей вектор-строкой – А5. Найденное число 5 означает, что, исходя из запасов имеющегося сырья S1,S2 и S3, мы не можем выпустить продукцию P1 в количестве, большее, чем 5.

Переходим ко II -ой итерации, включив в базис вектор А1 вместо вектора А5, что означает: выпуск продукции P1 в количестве 5 единиц, при этом сырье вида S3 полностью расходуется, т.е. x5 0. Третью строку новой таблицы получаем делением всей строки на разрешающий элемент 2. Для каждого базисного вектора заполним соответствующие значения C . Эти базисные вектора А3, А4,А1 будут единичными и соответствующие оценки будут равны нулю, т.е. 3 4 1 0. Остальные элементы векторов В,А2,А5 новой таблицы вычислим из предыдущей таблицы методом Жордана-Гаусса (т.е. по правилу прямоугольника).

Получили новый	опорный план	X1 (5;0;11;3;0), при котором
выпускается продукция	P1 в количестве 5	единиц, а сырье видов S1 и S2
остается соответственно в количествах 11		и 3 единиц. При этом прибыль

составляет F1 150 (денежных единиц). Данный план опять проверяем на оптимальность. Среди j есть отрицательное число (-20); поэтому план X1

не является оптимальным. Переходим к III -ей итерации, используя предыдущий алгоритм вычисления. Включаем в базис вектор А2 вместо вектора А4 , что означает: выпуск продукции P2 в количестве 3 единиц, при этом сырье вида S2 полностью расходуется, т.е. x4 0. Вторую строку новой таблицы получаем делением всей строки на разрешающий элемент 1. Для каждого базисного вектора заполним соответствующие значения C . Эти базисные вектора А3, А2,А1 будут единичными и соответствующие оценки будут равны нулю, т.е. 3 2 1 0. Остальные элементы векторов В,А4,А5 новой таблицы вычислим из предыдущей таблицы методом Жордана-Гаусса (т.е. по правилу прямоугольника).

После III-ей итерации все j 0, и полученный новый план X2

является оптимальным: X* (5;3;2;0;0).

Экономический смысл оптимального плана X*: для получения максимальной прибыли, равной 210 денежных единиц, исходя из имеющихся запасов сырья S1 21, S2 8, S3 10, необходимо выпустить продукцию P1 в количестве 5 единиц, продукцию P2 в количестве 2 единицы, при этом сырья S1 останется неизрасходованным в количестве 2 ед., а сырье S2 и S3 полностью израсходуется.

Упражнения

Найти оптимальный план производства продукции симплексным

методом:
4.1.					4.2.
СЫРЬЕ		ИЗДЕЛИЯ		ЗАП			СЫРЬЕ	ИЗДЕЛИЯ		ЗАПАС
		А	В	АСЫ				А	В	Ы
S1		12	3	684			S1	16	4	784
S2		10	5	690			S2	8	7	552
S3		3	6	558			S3	5	9	567
ПРИБЫ		6	2				ПРИБЫ	4	6
ЛЬ							ЛЬ
4.3.							4.4.

	СЫРЬЕ	ИЗДЕЛИЯ		ЗАП
		А	В	АСЫ
	S1	8	3	864
	S2	7	6	864
	S3	4	9	945

	СЫРЬЕ	ИЗДЕЛИЯ		ЗАПАС
		А	В	Ы
	S1	11	3	671
	S2	8	4	588
	S3	5	3	423

ПРИБЫ		2		3
ЛЬ
4.5.
СЫРЬ		ИЗДЕЛИЯ			ЗАП
Е		А		В	АСЫ
S1		15		4	1095
S2		11		5	865
S3		9		10	1080
ПРИБ		3		2
ЫЛЬ
4.7.
СЫРЬЕ		ИЗДЕЛИЯ			ЗАП
		А		В	АСЫ
S1		6		3	714
S2		5		10	910
S3		3		12	948
ПРИБЫ		3		9
ЛЬ
4.9.
СЫРЬЕ		ИЗДЕЛИЯ			ЗАП
		А		В	АСЫ
S1		3		5	453
S2		4		8	616
S3		3		11	627
ПРИБЫ		2		5
ЛЬ

	ПРИБЫ		5		2
	ЛЬ
4.6.
	СЫРЬЕ		ИЗДЕЛИЯ			ЗАПАС
		А		В		Ы
	S1		9		5	1431
	S2		7		8	1224
	S3		4		16	1328
	ПРИБЫ		3		2
	ЛЬ
	4.8.
	СЫРЬЕ		ИЗДЕЛИЯ			ЗАПАС
		А		В		Ы
	S1		9		4	801
	S2		6		7	807
	S3		3		8	768
	ПРИБЫ		3		2
	ЛЬ
	4.10.
	СЫРЬЕ		ИЗДЕЛИЯ			ЗАПАС
		А		В		Ы
	S1	10			9	1870
	S2		5		11	1455
	S3		4		15	1815
	ПРИБЫ		7		9
	ЛЬ

§5. Метод искусственного базиса

Чтобы решить задачу линейного программирования, записанную в канонической форме, симплексным методом необходимо, чтобы количество единичных векторов равнялось количеству уравнений в системе. Если же единичных векторов меньше количества уравнений, то задачу решают методом искусственного базиса. Для этого вводят дополнительные единичные вектора, которые называются искусственными, и получают расширенную задачу, которая имеет опорный план, и, следовательно, решается обычным симплексным методом.

В симплекс-таблице первые m строк определяются исходными данными задачи, а значения:

F (C ,B)				(5.1)
и:
j	(C ,Рj ) cj , ( j		)	(5.2)
		1,n

m	m
где (C ,B) cibi	и (C ,Рj ) ciaij ,	( j	1,n	),
i 1	i 1

записывают в две строки, т.е. в m 1 -ую и m 2 -ую строки, так как искусственная переменная в целевую функцию вводится с коэффициентомМ , где M - некоторое достаточно большое положительное число, конкретное значение которого обычно не задается.

При конкретных вычислениях значения F и j содержат две слагаемые,

одно из которых содержит M , а другое – нет. Для удобства итерационного процесса число, стоящее при M , записывают в m 2 -ую строку, а слагаемое, которое не содержит M , - в m 1 -ую строку и продолжают решение задачи обычным симплексным методом.

Алгоритм решения задач методом искусственного базиса

1.Составляют расширенную задачу.

2.Находят опорный план расширенной задачи.

3.С помощью обычных вычислений симплексного метода исключают искусственные векторы из базиса. В результате либо находят опорный план исходной задачи, либо устанавливают ее неразрешимость.

4.Найденный опорный план проверяют на оптимальность.

Задача. Требуется найти максимум функции:

	Fmax 2x1 x2
	2x1 3x2 9
при		2x2 2
	x1
	x	x		2	8
	1
	x	, x	2		0
	1

Приведем функцию к канонической форме:

	Fmax 2x1					x2					0x3 0x4			0x5
	2x1 3x2 x3 9
при		2x2 x4								2
	x1
	x	x		2	x			5	8
	1
	x , x		2	, x		3	, x			4	, x	5	0
	1

Запишем систему в векторной форме:

Р1x1 Р2x2 Р3x3 Р4x4 Р5x5 В.

Среди векторов:

	2			3			1			0		0
P1	1 ,P2 2 ,P3						0 ,P4 1 ,P5 0
	2			1			0			0
												1

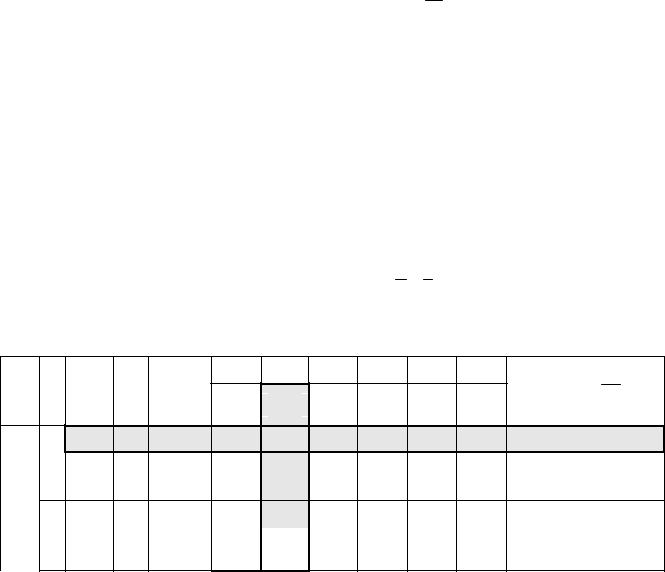
только два единичных вектора, уравнений – три. Введем дополнительный

1
единичный вектор P6 0		, т.е. в первое уравнение добавим
	0

неотрицательную искусственную переменную x6

с коэффициентом

М .

Получим следующую расширенную задачу:

Fmax 2x1

x2

0x3

0x4

0x5 Mx6

2x1 3x2 x3 x6 9

при

2x2 x4

2

.

x1

x

x

2

x

5

8

1

x , x

2

, x

3

, x

4

, x

5

,

x

6

0

1

Расширенная задача

имеет

первоначальный опорный

план

X0 (0; 0; 0; 2; 8; 9), определяемый

системой трех единичных векторов:

P4, P5, P6 . Составляем

таблицу I-ой

итерации, содержащую 5 строк. Для

заполнения 4-ой и 5-ой строк находим f0 и j ( j 1,6):

f0 C В M 9 0 2 0 8 9M 0,1 C P1 C1 M ( 2) 0 1 0 1 2 2M 2,

			2 3M 1,				3 M 0, 4 5 6 0.
	Значения f0 и			j	содержат две слагаемые, одно из которых содержит
M , а другое – нет. Число, стоящее при									M , записываем в 5 -ую строку, а
слагаемое, которое не содержит M , - в 4 -ую строку.
	В 5-ой строке			в	столбце		P2	имеется отрицательное число (-3), что
означает, что опорный план не является оптимальным. Переходим к новому
опорному			плану. В базис			вводим		вектор P2 . Чтобы определить						вектор,
исключаемый из				базиса,		находим				9	8	3. Значит, из		базиса
								min		,
										3	1
исключаем вектор P6, который является искусственным и, следовательно, не
имеет смысла в следующей итерации заполнять столбец P6.														b
					2		-1	0	0		0	-М
		Баз														i
	№		С	В									min
		ис			P		P	P	P		P	P		a
																ij
					1		2	3	4		5	0
	1	P6	-М	9	-2		3	-1	0		0	0	9:3=3		←
	2	P4	0	2	1		-2	0	1		0	1	-----
I	3	P5	0	8	1		1	0	0		1	0	8:1=8

4	j	f0 0	-2	1	0	0	0	0	X0=(0;0;0;2;8;9)
5		-9	2		1	0	0	0
				-3
				↑