§ 2. Методи обробки експертної інформації

Методи обробки експертної інформації поділяються на три основні групи: статистичні методи, алгебраїчні методи й методи шкалювання. Статистичні методи базуються на припущенні, що відхилення оцінок експертів від істинних значень відбувається у силу випадкових причин. Суть алгебраїчних методів полягає у такому: на множині допустимих оцінок задається відстань і результуюча оцінка визначається як така, відстань якої до оцінок експертів (за певним критерієм) мінімальна. Ідея методів шкалювання полягає у тому, що за експертною інформацією про степінь відмінності об'єктів установлюється мінімальний (або близький до мінімального) набір критеріїв та оцінок об'єктів за цими критеріями, що зумовлюють вказані експертами відмінності.

Статистичні методи

Експертиза 1 (Е1): Ω = Ω =^ E¹ , L – експерти ізольовані, Q – оберне-

n

ний зв'язок відсутній, a = ϕa₁,...,a_n ⁼ ∑α_ia_i .

i=1

Тобто результуюча числова оцінка a знаходиться за формулою середньозваженого значення (математичного сподівання випадкової величини). Степінню узгодженості думок експертів є дисперсія:

n σ^{2 =} ∑α_i (a −a_i )² .

i=1

Як модифікація (Е1) розглядається така експертиза 2: Ω = Ω =^ E³ ,

1 2 3 1 2 3 ) n i γ1ai1 + γ2ai2 + γ3ai3 i1

a = ϕa a a1, 1 , 1 ;...;a a an , n , n = ∑i 1 α γ + γ + γ1 2 3 , де a – "оптимістич-

=

на" оцінка i -го експерта, a_i² – "реалістична" і a_i³ – "песимістична".

Для експерта – "реаліста" (психологічний тип експерта можна визначити відповідним тестуванням) доцільно покладати γ₁ =1, γ₂ = 4, γ₃ =1; для експерта – "оптиміста" γ₁ = 3, γ₂ = 0, γ₃ = 2 (він "завищує" оптимістичну оцінку), для експерта – "песиміста" γ₁ = 2, γ₂ = 0, γ₃ = 3

(він "занижує" оптимістичну оцінку). Степінь узгодженості між оцінками визначається величиною

n

σ2 = ∑n α σ +i i2 ∑αi (a −ai )2 ,

i=1 i=1

де – степінь невпевненостіi -го експерта у своїй оцінці (для експерта реаліста γ₄ = 36, для інших – γ₄ = 25).

В експертизах E1, E2 можна визначити статистичну значимість отриманих результатів. Задаємо ймовірність похибки p , вважаючи, що величина a розподілена за нормальним законом із центром a і дисперсією σ² . Тоді: a − Δ ≤ a ≤ a + Δ , де Δ = σt n , величина t має розподіл Ст'юдента з (n −1)-м степенем свободи (визначаємо за таблицею розподілу Ст'юдента, за величиною р).

Опишемо застосування метода Делфі для Е1 у вигляді такої експе-

ртизи 3: Ω = E¹ , Ω = ^⎧_⎨z ∈E^k_∑^k z_i =1, z_i ≥ 0^⎫_⎬.

⎩ i=1 ⎭

Відображення φ задається так. Весь інтервал допустимих значень величин, що оцінюються, розбивається на k інтервалів: t₁,...,t_k . Експерт оцінює ймовірність попадання величини, що оцінюється, у кожен з k інтервалів. Нехай p_ij – оцінка ймовірності попадання у j -й інтервал, що дається i -м експертом. Тоді ймовірність попадання величини в інтервал t_j на основі думок усіх експертів оцінюється вели-

чиною: p_tj ⁼ ∑α_i p_ij , j =1,k .

i

За колективну оцінку береться медіана q₂ побудованого розподілу, яка визначається з умови: p t( ≤ q₂ ) = 0,5.

Емпірично встановлено, що процедуру можна зупиняти, коли діапазон квантілів Δq = q₃ − q₁ (де p t( ≤ q₃ ) = 0,75, p t( ≤ q₁) = 0,25) зменшився в 1,6 рази порівняно з початковим [5].

Експертиза 4 полягає у зіставленні індивідуальним ранжуванням експертів колективного ранжування: Ω = Ω =^{множина всіх перестановок m об'єктів}, експерти ізольовані, обернений зв'язок відсутній.

Відображення φ визначається так. Кожен експерт задає місце (ранг) кожного об'єкта: r_ij – ранг j -го об'єкта, визначеного i -м експертом.

n

Об'єкти впорядковуються відповідно до величин r_j = ∑r_ij , j =1,m (су-

i=1

ма рангів кожного об'єкта по всіх експертизах; вважаємо, що експерти мають рівну компетентність) – на перше місце ставиться об'єкт з мінімальним r_j і т. д. Колективне ранжування може бути нестрогим (ми розглядаємо випадок строгих індивідуальних ранжувань).

Степінь узгодженості думок експертів визначається за допомогою "коефіцієнта конкордації" W , що визначається нижче. Розглянемо два крайніх випадки:

• ранжування всіх експертів співпадають;

• усі ранжування відмінні (вважаємо, що n < m !).

m m n n m

Оскільки ∑ ∑∑ ∑∑r_j = r_ij = r_ij = 0,5⋅nm m( +1) (експерти задають

j=1 j= =1 i 1 i=1 j=1

m

ранги від 1 до m ), то "середній ранг" r_c = 1m^∑j₌1r_j = 0,5⋅n m( +1) і за узгодженість експертів беруть суму квадратів відхилень r_j від середнього значення r_c . Коефіцієнтом конкордації W для випадку строгих індивідуальних ранжувань називається величина:

W =12∑jm=1 ⎛⎜⎝rj − 12n m( +1)⎠⎞⎟2 n2 (m3 −m).

У випадку нестрогих індивідуальних ранжувань (Експертиза 5) об'єктам, які "ділять" місця, приписуються рівні ранги (так, якщо два об'єкти ділять місця 2–3, то кожен із них отримує ранг 2,5). Коефіцієнт конкордації для нестрогого ранжування:

W =12∑jm1 ⎛⎜⎝rj − 12n m( +1)⎞⎠⎟2 ⎛⎜⎝n2 (m3 −m) −n∑∑in=1 jk=i1 (tij3 −tij )⎞⎠⎟,

=

де k_i – число груп рівних рангів, введених i -м експертом; t_ij – кількість об'єктів у j -й групі, введеної i -м експертом.

Статистичну значимість ранжування перевіряють так. Вибирається допустима ймовірність похибки p ; вважається, що величина n m( −1)W має χ² – розподіл з (m −1) – м степенем свободи. За таблицею розподілу χ² знаходиться W_p і, якщо W ≥W_p , то отримане ранжування вважається статистично значимим (тобто значимим є узгодженість думок експертів). Якщо експерти не рівнокомпетентні, α_i –

n

вага i -го експерта, то r_j = ∑α_{i ij}r , інші формули залишаються без змін

i=1

n

(оскільки ∑α =_i 1).

i=1

Експертиза 6 визначається для задачі знаходження колективного ранжування за нестрогими індивідуальними ранжуваннями за допомогою попарних порівнянь об'єктів.

Множина Ω така ж, як і в E5; експерти ізольовані, обернений зв'язок відсутній, Ω^ – множина всіх матриць A = (a_ij ), де a_ij ∈{0,1},

a_ij +a _ji =1 (i ≠ j ), a_ii = 0, i, j =1,m . Кожен експерт робить C_m² порівнянь, порівнюючи кожен об'єкт із кожним. Результат порівнянь i -го експерта представляється матрицею Aⁱ розмірності m m× , у якій aⁱ_jk =1 тоді й лише тоді, коли для i -го експерта об'єкт j переважає об'єкт k . Для будь-якої пари об'єктів або перший переважає другого, або навпаки; a _jj = 0 за визначенням.

Матриця Aⁱ , що задається i -м експертом (i =1,m ), є матрицею деякого бінарного відношення, яке називається відношенням переваги i -го експерта. Очевидно, що бінарне відношення, що задається мат-

рицею Aⁱ є повним, антирефлексивним, антисиметричним і, взагалі кажучи, не є ациклічним.

Визначення 3.2.1. Відношення переваги з матрицею A може бути виражене рангами, якщо всі об'єкти, упорядковані так, що a _jk =1 тоді й лише тоді, коли ранг j -го об'єкта менший за ранг k .

Теорема 3.2.1. Необхідною й достатньою умовою того, що перевага виражається рангами, є ациклічність відношення переваги.

Теорема 3.2.2. Властивості відношень переваги Aⁱ приводять до еквівалентності умов ациклічності та наявності циклів довжини 3.

Відображення φ в Е6 визначається так. Будується матриця

A ⁼ (a _jk ) ⁼ _∑ⁿ Aⁱ , де A^{i =} (aⁱ_jk ) – матриця оцінок i -го експерта. Знахо-

i=1

m

дяться величини a _j = ∑a _jk , j =1,m . Об'єкт із максимальним a _j отри-

k=1

мує ранг 1 (він переважає максимальну кількість інших об'єктів) і т. д. Коефіцієнтом сумісності думок експертів називається величина:

⎧⎪1 24− d m³ −m, якщо т непарне, υ = ⎨₃

⎪⎩1 24− d m − 4m, якщо т парне,

де d – число циклів довжини 3 у матриці A . Величину υ для матриці

Aⁱ можна використовувати як оцінку компетентності i -го експерта.

Алгебраїчний метод

Для визначення колективної числової оцінки алгебраїчним методом використовується експертиза 7: Ω = Ω =^E¹ , експерти ізольовані, обернений зв'язок відсутній. Відстань d між числовими оцінками a і b визначається як d a b( , ) = a −b . За колективну оцінку a беруться, наприклад, оцінки:

n

• a ∈ Argmina E1 ^∑α_id a a( , _i ) (утилітарний критерій),

_∈ i₌1

• a ∈ Argminm₁ ax α_id a a( , _i ) (егалітарний критерій).

a E∈ i=1,n

Для визначення колективного ранжування алгебраїчним методом експерти задають матриці A^{i =} (aⁱ_jk ), у яких aⁱ_jk =1 тоді й лише тоді, коли об'єкт i передує об'єкту k ; якщо об'єкти j і k рівноцінні або j = k , a _jk = 0; якщо a _jk =1 ( j ≠ k ), то a_kj = −1.

Ранжування A і відповідну йому матрицю A будемо позначати одним символом.

Визначення 3.2.2. Ранжування C знаходиться між ранжуваннями

A і B , якщо для ∀i, j =1,m a_ij ≤ c_ij ≤ b_ij або a_ij ≥ c_ij ≥ b_ij .

Відстань між ранжуваннями вводиться аксіоматично: А1. d A B( , ) ≥ 0, причому d A B( , ) = 0 ⇔ A = B ;

А2. d A B( , ) = d B A( , ) (симетричність);

А3. d A B( , ) + d B C( , ) ≥ d A C( , ), причому рівність досягається тоді й лише тоді, коли ранжування B знаходиться між ранжуваннями A і C (аксіома трикутника);

А4. При однакових перестановках об'єктів у ранжуваннях A і B відстань між отриманими ранжуваннями d A B( ′, ′) = d A B( , ) (інваріантність відносно позначень);

А5. Якщо двоє ранжувань відрізняються одне від одного лише на частині об'єктів, то відстань між початковими ранжуваннями дорівнює відстані між ранжуваннями лише цих об'єктів;

А6. Мінімальна додатня відстань між ранжуваннями дорівнює 1.

Теорема 3.2.3. Аксіоми А1–А6 однозначно визначають відстань (відстань Хемінга) d A B( , ) при будь-якій довжині ранжувань m ≥ 2, а

m

формула: d A B, = 0,5⋅ ∑a_ij −b_ij , визначає єдину відстань d A B( , ),

i j, =1

що задовольняє аксіомам А1–А6.

Експертиза 8: Ω = Ω =^{матриці A_i , елементи яких визначені вище}, експерти ізольовані, обернений зв'язок відсутній. За відстань береться відстань Хемінга, колективне ранжування визначається критеріями:  A^KS ∈ ArgminA A^∑α_id A A( , ⁱ ) (медіана Кемені–Снелла); n

_∈ i₌1

• A^VG ∈ ArgminmA A∈  i₌1a,m^x α_id A A( , ⁱ ) (компроміс);

• A^SZ ∈ Argmin∑n α d² (A A, ⁱ ) (середнє значення).

A A∈  i=1 _i

Вище A^ – множина матриць m m× з елементами a_ij ∈ +{ 1, 1,− 0}, що відповідають ранжуванням (тобто матриці ациклічні). Як видно – критерій 1 відповідає принципу утилітаризма, критерій 2 – егалітаризма.

Приклад. Нехай n = m = 3, A¹ = A² =< a b c, , > , A³ =< b a c, , > (позначення < a b c, , > означає: a b c ). Випишемо відповідні матриці:

⎛ 0 1 1⎞ ⎛ 0 −1 1⎞

A¹ = A² = ⎜^⎜−1 0 1⎟^⎟, A³ = ^⎜⎜ 1 0 1^⎟⎟.

⎜⎝−1 −1 0⎟⎠ ⎜⎝−1 −1 0⎟⎠

Потрібно знайти медіани 1, 2 на множині матриць, що відповідають ранжуванням: A₁ =< a b c, , >, A₂ =< a c b, , >, A₃ =< b a c, , >.

A₄ =< b c a, , >, A₅ =< c a b, , >, A₆ =< c b a, , >. Виписуємо відповідні матриці: A₁ = A = B , A₃ = C ,

⎛ 0 1 A2 = ⎜⎜−1 0 ^⎜−1 1 ⎝

1 ⎞ ⎛0 −1⎟⎟, A4 = ⎜⎜1 0 ⎟⎠ ⎜⎝1

−1 0 −1

−1⎞ ⎟ 1 ⎟, A5 = 0 ⎟⎠

⎛ 0 1 ^⎜−1 0 ⎜ ^⎜1 1 ⎝

−1⎞ ⎛0 −1⎟⎟, A6 = ⎜⎜1 0 ⎟⎠ ⎜⎝1

−1 0 1

−1⎞ −1^⎟⎟. 0 ⎟⎠

Знаходимо: d A A( 1, ¹) = d A A( 1, ² ) = 0,d A A( 1, ³ ) = 2; d A A( 2, ¹) = d A A( 2, ² ) = 2,d A A( 2, ³ ) = 4; d A A( 3, ¹) = d A A( 3, ² ) = 2,d A A( 3, ³ ) = 0; d A A( 4, ¹) = d A A( 4, ² ) = 4,d A A( 4, ³ ) = 2; d A A( 5, ¹) = d A A( 5, ² ) = 4,d A A( 5, ³ ) = 6; d A A( 6, ¹) = d A A( 6, ² ) = 6,d A A( 6, ³ ) = 4.

Таким чином, A^KS = A^VG = A^SZ = {A A₁, ₃} (цього слід було очікувати, оскільки ранжування двох експертів збіглися, ранжування третього відрізняються від їхнього ранжування лише однією перестановкою). Нехай, A¹ = A₁ , A² = A₄ , A³ = A₆ . Тоді A^KS = {A A₃, ₄}, A^VG = {A₃}, A^SZ = {A₃}.

Методи шкалювання

У методах шкалювання експерти оцінюють попарні відмінності між об'єктами, вказують відповідні числа. Задача полягає у зіставленні кожному об'єкту точки простору E^r , r ≥1, а всій системі, що складається з m об'єктів, m точок у E^r так, щоб відстані у E^r між точками були достатньо близькими до вказаних експертами чисел. Таким чином, розв'язок задачі оцінювання у цьому випадку є вектором довжини m r⋅ .

Експертиза 9 (одновимірне шкалювання): Ω = E^m , Ω =^{нестрогі ранжування}, експерти ізольовані, оберненого зв'язку немає. Для побудови φ необхідно зробити такі операції:

n

• Обчислюється матриця P = ∑Aⁱ /n , де Aⁱ – матриця, що відпо-

i=1

відає ранжуванню, даному i -м експертом. Елементи p_jk матриці P – імовірності переваги j -го об'єкта над k -м.

• За заданими p_jk обчислюються величини z_ij за формулами:

z _jk p_jk = _∫ π e dt за таблицями нормального розподілу.

−∞

• Формується матиця Z ⁼z _jk ), знаходяться величини z _j = ∑z _jk . m

k=1

Оцінкою об'єкта A_j є середнє z = z /m , j =1,m .

• Визначаються величини p за формулою:

p = G z( 2π e dt . (3.2.1)

m

Нормалізовані величини p p_j називаються показниками

j=1

відносної важливості об'єктів.

• Здійснюється перевірка на несуперечність. Для цього за формулою (3.2.1) знаходяться p_jk = G z( _j − z_k ) і обчислюються величини

m

Δ _jk = p_jk − p_jk . Визначається середнє відхилення Δ _jk = ∑ Δ _jk /m m( −1),

j k, =1 j k<

достатня малість якого свідчить про несуперечність ранжувань експертів.

Задача багатовимірного метричного шкалювання полягає у наступному. Задається симетрична матриця відмінностей D = (D_jk ) між m об'єктами A₁,...,A_m на основі агрегування думок n експертів (наприклад, так, як у попередній експертизі). Необхідно знайти координати m точок a ^j ∈E^r , що відповідають об'єктам, так, щоб матриця

X = (x _jk ) відстаней між цими точками була близькою до матриці початкових відмінностей D за певним критерієм. Якщо значення критерію обертається у нуль, то говорять, що задача має точний розв'язок.

В основі Експертизи 10 лежить метод простої ординації, який полягає в такому.

Розглянемо спосіб побудови точок a¹,...,a^m ∈E^m , що відповідають об'єктам A₁,...,A_m . За A₁ і A₂ оберемо об'єкти, відстань D_jk між якими в агрегованій матриці D максимальна. Тоді a₁¹ = 0, a₁² = D_jk ;

a¹_j = a²_j = 0, j = 2,m . Побудовані точки належать півпростору E¹,

утвореного першою віссю E^m .

Нехай E^r – r -вимірний півпростір, що утворюється осями з номерами 1,...,r , у якому вже знайдено точки a¹,...,a^{r +1}. У цих точок у E^m усі координати, починаючи з (r +1)-ї, дорівнюють нулю. Проекції інших точок a_r +₂,...,a_m в E^r знаходяться із заданих відстаней D_jk між

об'єктами j і k , j,k =1,m . Нехай координати проекції точки a^l ,

l > r +1, в E^r – це a₁^l ,...,a_r^l , h_l – відстань між точкою a^l й підпросто-

ром E^r . Маємо: ,

s=1

r

j =1,r +1⇒ h_l² = D²_jl ⁻ _∑(a_s^j −a_s^l )2 , j =1,r +1. (3.2.2)

s=1

Ліва частина останньої рівності не залежить від a ^j . Прирівнюючи праві частини при j і j +1, отримаємо систему r рівнянь відносно r невідомих a₁^l ,...,a_r^l :

D2jl − ∑(asj −asl )² = D2j+1,l − ∑(asj⁺¹ −a_s^l )² , j =1,r . r r

s=1 s=1

Розв'язавши цю систему при l = r + 2,m , отримаємо проекцію точки

a^l в E^r . Із рівності (3.2.2) знайдемо h_l для l = r + 2,m й покладемо

arl +1 = hl .

Оберемо об'єкт A_j , для якого h _j = maxh_l . Зіставимо йому у просто-

l r= +2,m

рі E^m точку a ^{j =} (a₁^j ,...,a h_r^j , _j ,0,...,0). Перенумеруємо об'єкти A_{r +2},...,A_m так, щоб вибраний об'єкт мав номер r + 2. Таким чином, отримали координати точки a^{r +2} й проекції точок a^{r +3},...,a^m у простір E^{r +1} . Критерій завершення процесу вибирається так:α =1− s s, де

m

s a a , s ⁼ ∑ D²_jk . j k, =1 s=1 j k, =1 j k< j k<

Якщо α менше вибраного ε > 0, обчислення координат точок припиняємо і образами об'єктів A₁,...,A_m вважаються проекції точок a¹,...,a^m в E^r .

В основі експертизи 11 (метод "трійок") лежать такі теоретичні побудови. Розглянемо трикутник зі сторонами D_ij ,D_ik , D_jk (рис 3.2.1). За теоремою косинусів:

D Dij ik cosΘ = (Dij2 + Dik2 − D2jk )/2.

ai Dik ak

Рис. 3.2.1

Побудуємо матриці Bⁱ , i =1,m , з елементами: bⁱ_jk ⁼ (D_ij² + D_ik² − D²_jk )/2. Наступні властивості матриць Bⁱ визначають

існування точного розв'язку задачі метричного шкалювання й мінімальну розмірність простору E^r , при якому точний розв'язок існує.

Теорема 3.2.4. У випадку додатної напіввизначеності матриць Bⁱ ,

i =1,m (тобто (B x xⁱ , ) ≥ 0 для ∀x ) задача метричного шкалювання має точний розв'язок. Мінімальна розмірність простору E^r , r = minρ_i , де

i

ρ_i – ранг матриці Bⁱ , i =1,m . За образи об'єктів A_s , s =1,m , s ≠ i , у просторі E^r можна взяти точки a^s = (a₁^s,...,a_r^s ), s =1,m , такі, що

Bⁱ = XX ^T , X ⁼ (x _pq ), де x_pq = a_q^p , p =1,m , p ≠ i , q =1,r , a_i^l = 0, l =1,r .

У розглянутих випадках відображення φ є лінійним. У загальному ви-

падку неможлива побудова точок a ^j , j =1,m , у просторі достатно малої розмірності E^r із збереженням бажаної точності. Тому використовуються нелінійні методи, що базуються на інтерполяційних процедурах.

Основою Експертизи 12 ("нелінійне багатовимірне шкалювання") є така процедура. Упорядкувавши за зростанням m² елементів матриці відмінностей D , отримаємо лінійний порядок r A( ). Відобразимо об'єкти A_j у простір E^r , лінійний порядок зі зростання елементів мат-

риці X відстаней між точками a ^j , j =1,m , позначимо через r a( ).

Виконуємо операції:

1. Будуємо ранжування r A( ) і нормалізуємо елементи матриці D так, щоб мінімальний дорівнював нулю, максимальний – одиниці.

Отриману матрицю позначимо через D^.

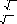
2. Точки a ^j , j =1,m , знаходимо як вершини правильного (m −1)вимірного симплекса, центр якого знаходиться у початку координат, ребра мають довжину 1. Координати вершин симплекса обчислюються за формулами: a₂^j_q−1 = cos 2 ([ q j −1)π/m]/ m , a₂^j_q = sin 2 ([ q j −1)π/n]/ m ,

де q =1,[(m −1)/2] ([ ]x – ціла частина x ).

Для парного m проекція на (m −1)-у вісь: a_m^j ₋₁ = −( 1)^j−1 / 2m .

3. Будуємо ранжування r a( ). Якщо r a( ) = r A( ), то обчислення закінчується. Інакше нормуємо матрицю X відстаней між точками a ^j ,

j =1,m (аналогічно матриці D , крок 1), отримуючи X^.

4. Знаходимо нові значення координат точок a ^j , j =1,m , за формулами:

a_k^j = a_k^j + Δa_k^j , j =1,m −1,

α(D− x)(ai −a j ) β(D− D)(a^k −a^k )

де Δakj = ∑i j Pjik + Rkji , Pjik = ji xji ji k k , Rkji = ji D_ji i j ,

≠

m

_D ⁼ ∑ _D^_jim² ; α = 0,2, β = 0,05.

j i, 1=

5. Покладемо a ^j = a ^j , j =1,m , будуємо ранжування r a( ) і переходимо на крок 1.

Методи побудови кардинальних оцінок

У практичних задачах дуже часто важливо не лише вказати факт переваги одного об'єкта над іншим (або побудувати ранжування), але й оцінити ступінь цієї переваги.

Нехай ранжуванню об'єктів o₁ o₂ ... o_m відповідає вектор числових оцінок β = (β₁,...,β_m ).

Розглянемо основні методи визначення оцінок.

Метод фон Неймана–Моргенштерна (експертиза 13). Нехай m = 2. Маємо ранжування o₁ o₂ і об'єкту o₂ приписується оцінка β₂ =1.

Експерт вибирає таке значення величини , 0γ < γ ≤1, при якому, на його думку, γβ₁ = β₂ . З останього співвідношення маємо β =₁ 1γ .

Якщо m = 3, то β₃ =1 і експерт визначає значення γ₁,γ₂ з умов γ β_{1 1} = β₃, γ β_{2 2} = β₃ , звідки β =₁ 1γ1 ,β₂ = 1γ2 . Після цього експерт повинен визначити γ₃ з умови γ β_{3 1} = β₂ . Оцінки об'єктів вважаються узгодженими, якщо γ₃ ⁼ γ¹ γ2 , інакше експерт переглядає початкові зна-

чення γ₁^,γ₂ .

При m об'єктах число перевірок дорівнює

1 2 ...+ + +m − 2 = ^(m −^1)(m − ²⁾₂. Загальне число оцінок, які повинен встановити експерт, складається з m −1 початкових оцінок і ^(m −^1)(m − ²⁾2 вторинних оцінок, всього ^{m m(} −¹⁾2 = C_m² .

Отримані внаслідок оцінки β β₁, ₂,...,β_m є абсолютними. Для отримання відносних оцінок потрібно обчислити значення g_i =. β_j

Для підвищення "об'єктивності" процедури її можна легко узагальнити на випадок n експертів (використавши, наприклад, алгоритм, описаний в §§ 1, 2).

В експертизі 14 (метод Гергомена–Акофа) експерт будує ранжування (нехай це буде : o₁ o₂ ... o_m ).

Об'єкту o_m приписується оцінка β_m =1, останнім об'єктам експерт виставляє оцінки, порівнюючи їх з об'єктом o_m . Значення всіх оцінок повинно монотонно спадати зі зростанням порядкових номерів об'єктів.

Далі об'єкт o₁ послідовно порівнюється з "сумою" об'єктів o₂ +...+ o o_n , ₂ +...+ o_n−1,...,o₂ + o₃ до того часу, поки o₁ не стане еквіва-

лентним або кращим за відповідну "суму", тобто експерт вважає, що

s

β₁ ^≥ ∑β_i , s ≥ 3. Після цього експерт порівнює o₂ із "сумами"

i=2

l

∑o l_i , ≤ m, і т. д. У знайдені нерівності підставляються оцінки об'єктів

i=3

і якщо нерівності справедливі, то призначені експертом оцінки і є шуканими. Інакше оцінки коректуються.

У цьому методі кількість початкових оцінок дорівнює C_m² , але самі порівняння для експертів є складнішими, оскільки кожного разу один об'єкт порівнюється з декількома.