Варианты контрольных заданий

Решить следующие транспортные задачи:

1)	аі	2)	аі
3)	аі	4)	аі
5)	аі	6)	аі
7)	аі	8)	аі
9)	аі	10)	аі
11)	аі	12)	аі
13)	аі	14)	аі
15)	аі	16)	аі
17)	аі	18)	аі
19)	аі	20)	аі
21)	аі	22)	аі
23)	аі	24)	аі
25)	аі	26)	аі

Тема 6. Задача о назначениях

Пусть требуется выполнить nразличных работ и имеетсяn механизмов, причем каждый механизм может использоваться на любой работе.

С_ij – производительностьi-го механизма наj-той работе. Найти такое распределение механизмов по работам, при котором суммарная производительность максимальна.

Сопоставим каждому из возможных вариантов распределения машин по работам набор значений неизвестных х_ij .

х_ij =1, если в данном вариантеi-ый механизм назначен наj-тую работу.

х_ij =0, если в данном вариантеi-ый механизм назначен не наj-тую работу.

Для любого варианта среди чисел х_ij должно быть точноnединиц, причем должны выполняться условия:

(каждый механизм назначается на одну работу) и

(на каждую работу назначен один механизм)

Суммарная производительность:

Таким образом, математическая модель задачи будет:

_(6.1.)

(6.2.)

(6.3.)

Последние условия выводят задачу о назначениях из класса линейного программирования, так как они нелинейные. Это задачи с булевыми переменными.

Однако, практически эту задачу можно рассматривать как частный случай транспортной задачи. Действительно, если отбросить последние условия, заменив их условиями неотрицательности переменных, то задача превращается в обычную транспортную задачу, имеющую ту особенность, что в ней все a_i (i=1, 2, …,n) и всеb_j (i=1, 2, …,n) равны единице.

Эти особенности позволяют решить ее более просто, чем транспортную задачу.

Пусть 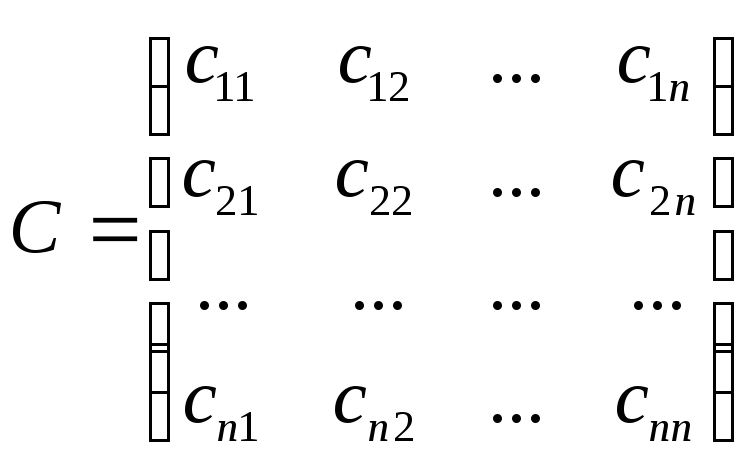– матрица эффективностей (например, производительноестей) задачи о назначениях. В соответствии с постановкой этой задачи, решить ее – значит выбрать в матрице С n элементов, по одному из каждой строки и каждого столбца так, чтобы сумма выбранных элементов, равная общей эффективности, соответствующей данному выбору, была наибольшей по сравнению с ее значениями при всех других таких выборах.

Введем определение:

Две матрицы С=(с_ij) и D=(d_ij) назовем здесь эквивалентными, если одна из них получается из другой прибавлением к элементам каждой строки одного и того же числа (может быть для различных столбцов эти числа различны, т.е. d_ij=с_ij+e_i+f_j

и – эквивалентны, т.к.Dполучается из С прибавлением к строкам С чисел 0, 0, 1, -1, а к столбцам – чисел 2,3,4,1 соответственно.

Практически задачу можно рассматривать как частный случай транспортной задачи. Действительно, если отбросить последние условия (6.4), заменив их условиями неотрицательности переменных, то задача (6.1)-(6.4) превращается в обычную транспортную задачу, имеющую ту особенность, что в ней все a_i (i=1, 2, …,n) и всеb_j (i=1, 2, …,n) равны единице. Если решить эту задачу методом потенциалов или любым другим методом, который при целыхa_i иb_j приводит к целочисленному оптимальному решению, то полученное решение автоматически будет удовлетворять не учтенному нами условию булевости переменных.

Особенности задачи (6.1) – (6.4) позволяют решить ее с помощью еще более простых приемов.

Пусть

Теорема: Множества оптимальных назначений двух задач с эквивалентными матрицами совпадают.

Приведенная теорема позволяет, если это потребуется, переходить от данной задачи выбора с матрицейСк задаче выбора с любой другой матрицейD, при условии, чтоDэквивалентнаС.

Нам удобно будет предварительно перейти от данной задачи выбора на максимум к задаче выбора с теми же условиями, но на минимум, т.е. от матрицы С=(с_ij) перейти к матрице –С=(–с_ij) и искать выбор, дающий минимальную сумму элементов.

Теперь перейдем от задачи на минимум с матрицей –Ск задаче на минимум с эквивалентной ей матрицей, которая имела бы только неотрицательные элементы и, в каждой строке и каждом столбце которой было бы хотя бы по одному нулевому элементу. Для этого сначала прибавим к каждому столбцу матрицы –С наибольший из элементов соответствующего столбца матрицы С. Получится неотрицательная матрицаС₁, в каждом столбце которой есть хотя бы один нуль. Теперь вычтем из каждой строки матрицыС₁ минимальный элемент этой строки. Полученная матрицаDи будет неотрицательной матрицей, в каждой строке и в каждом столбце которой есть хотя бы один 0.

Эти преобразования называются предварительными преобразованиями.

Дальнейший алгоритм.

1. Отмечаем (например, звездочкой) какой-нибудь нуль в 1 столбце матрицы D(0*), отмечаем звездочкой какой-нибудь нуль во 2-ом столбце, не лежащий в той строке, в которой находится 0* из первого столбца (если такой нуль во 2-ом столбце найдется); отмечаем один из нулей третьего столбца, лежащий в строке, где нет еще нулей со звездочкой и т.д., пока не пройдем все столбцы матрицы.

Если число отмеченных звездочкой нулей равно nто процесс окончен: места, занимаемые нулями со звездочкой соответствуютnпеременнымх_ij , равным 1.

Если нулей со звездочкой меньше n, то …

2. Помечаем (например, знаком "+" сверху) столбцы матрицы, в которых есть 0*, и считаем эти столбцы занятыми.

Будут появляться и занятые строки. Элементы, стоящие на пересечении незанятого столбца и незанятой строки будем считать незанятыми; остальные элементы – занятыми.

Если в матрице нет незанятых нулей, то переходим к п. 5.

Если незанятые нули есть, то выбираем первый из них (просматривая поочередно строки матрицы слева направо). Отмечаем его (например, штрихом – 0'). Если в его строке не нуля со звездочкой, то переходим к п.4; если в его строке 0* есть, то …

3. Освобождаем (снимаем знак "+" и считаем снова незанятым) столбец, в котором находится 0*, лежащий в той же строке, что и отмеченный только что штрихом нуль. Помечаем (например знаком "+") справа строку, в которой находится наш 0', и считаем ее занятой.Возвращаемся ко второй части п. 2 (3-й абзац п.2).

4. Начиная с только что отмеченного 0', строим цепочку из нулей: от этого 0' по столбцу к 0*, от него по строке к 0', и т.д., пока это возможно. Цепочка оборвется (возможно, на первых же 0') на некотором 0'. Снимаем звездочки у нулей из цепочки и заменяем звездочками штрихи у нулей из цепочки. Новый набор нулей со звездочками содержит на один больше, чем предыдущий и является также правильным.

Снимаем все пометки, кроме звездочек, и возвращаемся ко второй части п.1 (2 абзац п.1)

5. Отыскиваем минимальный элемент среди незанятых элементов матрицы (пусть он равен h) и вычитаем его из всех незанятых строк, а затем прибавляем ко всем занятым столбцам. Никакие пометки при этом не снимаются. Получается матрица, эквивалентная предыдущей и содержащая незанятые нули. Возвращаемся к третьей части п.2 (4-ый абзац п.2)

Пример:

Найти оптимальный вариант назначений, если матрица эффективностей такова:

Приводим цепочку матриц, получающихся в процессе решения задачи, с соответствующими пометками. Снятие значка отмечено заключением его в прямоугольник. Над стрелками переходов от матрицы указаны пункты алгоритма, которые использовались при соответствующих преобразованиях.

+

+

+

+

+

+

+

+

Процесс окончен, т.к. получилось n=5 нулей со звездочкой. Оптимальный вариант назначений:

х₁₅=х₂₄=х₃₁=х₄₃=х₅₂=1, остальныех_ij=0, т.е. первый механизм назначается на пятую работу, второй – на четвертую, третий – на первую, четвертый – на третью, пятый на вторую.

Изложенный алгоритм называется венгерским методом решения задачи о назначениях.