Варианты контрольных заданий
В задачах 1-25 найти maxFпри указанных ограничениях:
|
1) |
F=3x1+2x2-6x3
xi≥0;
(i= |
|
2) |
F=2x1+3x2-x3
xi≥0;
(i= |
|
3) |
F=8x1+7x2+x3
xi≥0;
(i=
|
|
4) |
F=x1+3x2-5x3
xi≥0;
(i= |
|
5) |
F=x1+2x2-x3
x1, x2, x3≥0
|
|
6) |
F=x1+2x5-5x6
xi≥0;
(i= |
|
7) |
F=8x1-3x2+x3+6x4-5x5
xi≥0; (i=1,5)
|
|
8) |
F=2x1-3x2+4x3+5x4-x5+8x6
xi≥0;
(i= |
|
9) |
F=-3x1+5x2-3x3+x4-x5+8x6
xi≥0;
(i=
|
|
10) |
F=5x1-x2+8x3+10x4-5x5+x6
xi≥0;
(i= |
|
11) |
F=10x1+14x2+12x3
xi≥0;
(i= |
|
12) |
F=4x1+x2-4x3
xi≥0;
(i=
|
|
13) |
F=x1-2x2+5x3
xi≥0;
(i= |
|
14) |
F=3x1-3x2-4x3
xi≥0;
(i= |
|
15) |
F=6x1-x2+3x3
xi≥0;
(i= |
|
16)0) |
F=-2x1-5x2-4x3
xi≥0;
(i= |
|
17) |
F=-3x1+4x2-6x3
xi≥0;
(i= |
|
18) |
F=x1+2x2-x3
xi≥0;
(i= |
|
19) |
F=10x1+14x2+12x3
xi≥0;
(i= |
|
20) |
F=9x1+6x2+4x3+7x4
xi≥0;
(i= |
|
21) |
F=3x1-7x2-4x4
xi≥0;
(i=
|
|
22) |
F=x1+3x2-5x4
xi≥0;
(i=
|
|
23) |
F=27x1+10x2+15x3+28x4
xi≥0;
(i=
|
|
24) |
F=3x1+2x2-6x3
xi≥0;
(i= |
|
25) |
F=3x1+2x5-5x6
xi≥0;
(i=
|
|
|
|
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
)
Тема 2. Двойственная задача линейного программирования
2.1. Постановка задачи
Задача: Для производства изделий А, В, С используется три различных вида сырья. Каждый из видов сырья может быть использован в количестве, соответственно не большем 180, 210, 244 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции каждого вида:
|
Вид сырья |
Нормы затрат на единицу продукции |
Количество сырья | ||
|
А |
В |
С | ||
|
І |
4 |
2 |
1 |
180 |
|
ІІ |
3 |
1 |
3 |
210 |
|
ІІ |
1 |
2 |
5 |
244 |
|
Цена единицы продукции |
10 |
14 |
12 |
|
Определить план выпуска продукции, при котором обеспечивается ее максимальная стоимость.
Математическая модель данной задачи следующая:
F=10x1+14x2+12x3–max
x1, x2, x3≥0
Оценить каждый из видов сырья, используемых для производства продукции. Оценки, приписываемые каждому из видов сырья, должны быть такими, чтобы оценка всего используемого сырья была минимальной, а суммарная оценка сырья, используемого на производство единицы продукции каждого вида – не меньше цены единицы продукции данного вида. Этой задаче соответствует следующая математическая модель:
F*=100y1+210y2+244y3–min
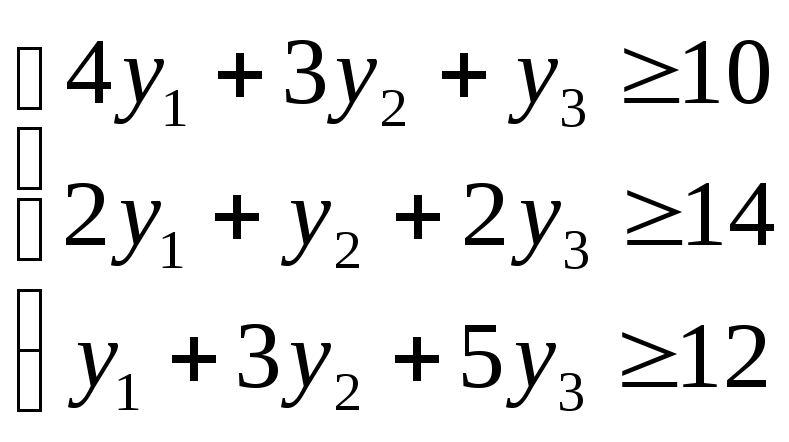
y1, y2,y3≥0
y1, y2,y3 – цена единицы сырья I, II, III видовa11y1 + a21y2 + a31y3 .
Тогда 4y1 + 3y2 + y3 можно трактовать как расходы на единицу продукции вида А и .т.д.b1y1 + b2y2 + b3y3 – суммарные расходы на производство.
y1, y2, y3 – "теневые цены".
Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой:
Прямая:
F(x)=c1x1+ c2x2+…+ cnxn→max
a11x1+ a12x1+…+ a1nxn≤b1,
a21x1+ a22x1+…+ a2nxn≤b2,
………………………………
ak1x1+ ak2x1+…+ aknxn≤bk,
ak+1,1x1+ ak+1,2x1+…+ ak+1,nxn=bk+1,
………………………………
am1x1+ am2x1+…+ amnxn=bm,
Двойственная:
F*(Y)=b1y1+ b2y2+…+ bmym→min
a11y1+ a21y2+…+ am1ym≥c1,
a12y1+ a22y2+…+ am2ym≥c2,
………………………………
a1ly1+ a2ly1+…+ amlym≤cl,
a1,l+1y1+ a2,l+1y2+…+ am,l+1ym=cl+1,
………………………………
a1ny1+ a2ny1+…+ amnym=cm,
Двойственная задача по отношению к исходной составляется согласно правилам:
Целевая функция исходной задачи задается на максимум, а двойственной на минимум.
Матрица из коэффициентов при неизвестных исходной задачи и аналогичная матрица двойственной задачи получаются друг из друга транспонированием.
Число переменных в двойственной задаче равно числу соотношений в системе ограничений исходной задачи, а число ограничений двойственной задачи - числу переменных в исходной задаче.
Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе исходной задачи, а правыми частями в системе ограничений двойственной задачи - коэффициенты при неизвестных в целевой функции исходной задачи.
Если переменная хj исходной задачи может принимать только лишь положительные значения, то j-e условие в системе ограничений двойственной задачи является неравенством вида "≥". Если же переменная хj может принимать и отрицательные значения, то j-e соотношение в двойственной задаче будет равенством. Если i-e соотношение в исходной задаче является неравенством, то і-я переменная двойственной задачи yi≥0. В противном случае yi может принимать как положительные, так и отрицательные значения.
Двойственные пары задач подразделяются на симметричные и несимметричные. В симметричной паре двойственных задач ограничения прямой и двойственной задач могут принимать лишь неотрицательные значения.