Лекции Дудорова(Оптимизация.) / lection_dudarov / Лекция 10

4

Лекция 10

Оптимизация методами детерминированного поиска.

Методы оптимизации функции одной переменной

Безградиентные методы детерминированного поиска используют информацию, получаемую от сравнительной оценки критерия оптимальности в результате выполнения очередного шага оптимизации.

Среди методов оптимизации функции одной переменной наибольшую эффективность показали:

• метод локализации экстремума;

• метод «золотого сечения»;

• метод поиска с использованием числе Фибоначчи.

Метод локализации экстремума

Дано:

y=R(x) определена на интервале [a, b];

 – точность вычислений

Найти:

x_min – ?

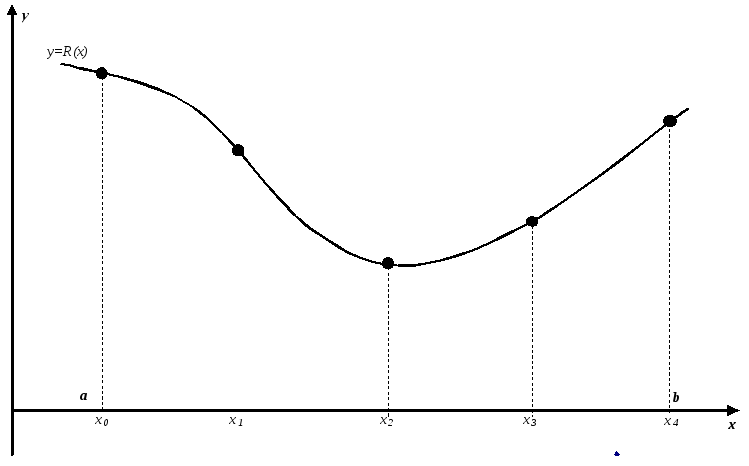
1. Исходный интервал [a, b] разбивается на четыре равные части:

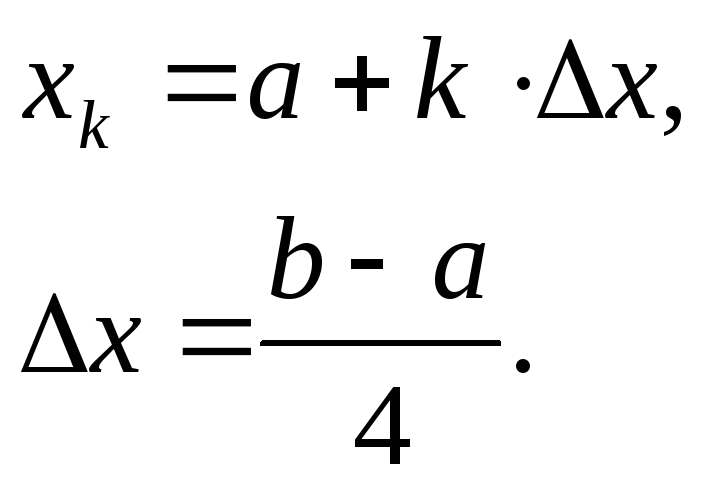
2. На границах всех подынтервалов (x_k) вычисляются значения функции R(x_k). Из рассчитанных значений определяется наименьшее R(x_{k, min}) (для критерия минимизации).

3. Определяются новые границы интервала:

4. Процедура повторяется с пункта 1 до тех пор, пока не будет выполнено условие окончания:

(1)

Задание 1. Найти глобальный минимум целевой функции вида на интервале [–10; 10] с точностью 0,1 методом локализации экстремума.

x0	x1	x2	x3	x4	R(x0)	R(x1)	R(x2)	R(x3)	R(x4)	
–10	–5	0	5	10	1907,7	3,1	11	–443,6	14,3	10,0
0	2,5	5	7,5	10	11	–156,5	–443,6	–561,1	14,3	5,0
5	6,25	7,5	8,75	10	–443,6	–550,8	–561,1	–401,9	14,3	2,5
6,25	6,88	7,5	8,13	8,75	–550,8	–572,2	–561,1	–507,8	–401,9	1,3
6,25	6,56	6,88	7,19	7,5	–550,8	–565	–572,2	–571,3	–561,1	0,6
6,56	6,72	6,88	7,03	7,19	–565	–569,6	–572,2	–572,9	–571,3	0,3
6,88	6,95	7,03	7,11	7,19	–572,2	–572,8	–572,9	–572,4	–571,3	0,2
6,95	6,99	7,03	7,07	7,11	–572,8	–572,9	–572,9	–572,7	–571,3	0,1

Метод «золотого сечения»

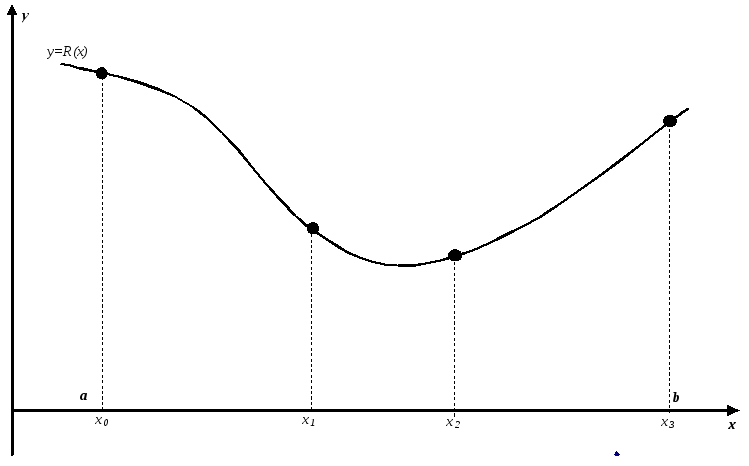
В отличие от первого метода, в этом случае исходный интервал делится на три неравных подынтервала. Особенность «золотого сечения» заключается в том, что если для исходного интервала [a, b] существуют точки x₁, x₂, такие, что , то для любого подынтервала [a, x₂] или [x₁, b] можно выбрать такую точку x*, что будет выполняться равенство 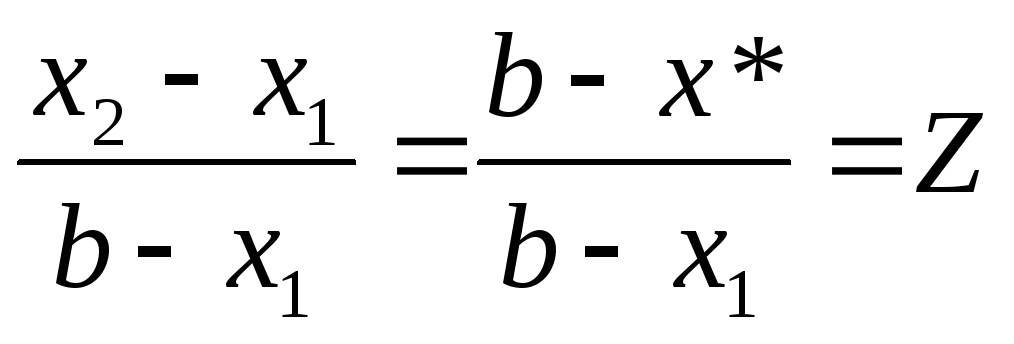, то есть на каждом шаге деление подынтервала будет подобно делению исходного интервала.

Число называется «золотым сечением».

1. Исходный интервал [a, b] делится на три подынтервала двумя промежуточными точками x* и x**:

2. В точках x*, x** вычисляются значения функции R(x).

3. Если R(x*)<R(x**) (для критерия минимизации), то:

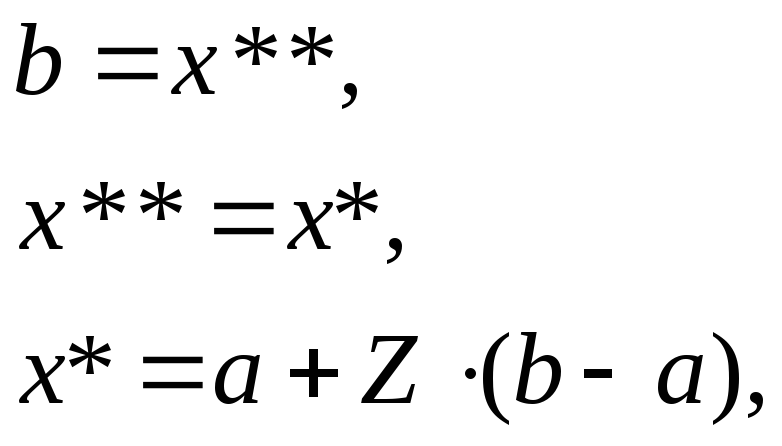
в противном случае:

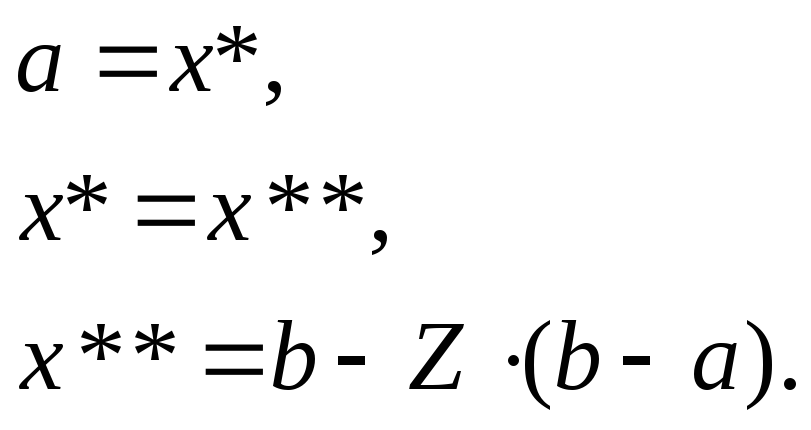
4. Процедура повторяется с пункта 2 до достижения заданной точности (1).

Метод поиска с использованием чисел Фибоначчи

Свойства последовательности чисел Фибоначчи описываются рекуррентным соотношением:

Таблица

Последовательность чисел Фибоначчи

k	0	1	2	3	4	5	6	7	8	9	10	11	12
Fk	1	1	2	3	5	8	13	21	34	55	89	144	233

1. Определяется число Фибоначчи F_s, такое, чтобы выполнялось неравенство:

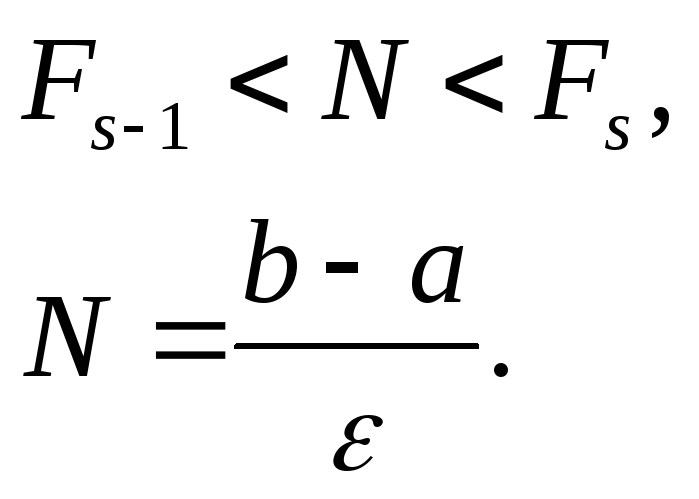
2. Рассчитывается минимальный шаг поиска:

3. Рассчитывается значения критерия минимизации в начале интервала (R(a)) и запоминается это значение как промежуточное значение минимума R_min=R(a).

4. Определяется промежуточная точка x*=a+F_s–2.

5. Рассчитывается значение R_curr=R(x*).

6. Если R_curr<R_min, x*=x*+F_s–3 и R_min=R_curr, в противном случае x*=x*–F_s–3.

7. Процедура с пункта 5 продолжается до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности.

Задание 2. Найти глобальный минимум целевой функции вида на интервале [–10; 10] с точностью 0,1 методом поиска с использованием чисел Фибоначчи.

Решение: N=20/0,1=200; F_s=233; =20/233=0,08584.

Rmin	Fs	x*	R(x*)	Знак
1907,7	89	–2,36	7,27	+
7,27	55	2,36	–142,4	+
–142,4	34	5,28	–472,8	+
–472,8	21	7,08	–572,6	+
–572,6	13	8,20	–498,1	–
–572,6	8	6,39	–557,9	–
–572,6	5	6,65	–567,8	–
–572,6	3	6,82	–571,5	–
–572,6	2	6,91	–572,6	–
–572,6	1	6,99	–572,9	+
–572,9	1	7,08	–572,6	–