Фадеев М.А. А-06-08
Московский энергетический институт
(технический университет)
Курсовая работа по курсу «Комбинаторика»
Студент Фадеев М.А.
Группа А-06-08
Преподаватель Набебин А.А.
Москва 2010
Задача №1.21
Преподаватель принимает зачет в группе из N + 10 человек. Найти число вариантов очередного опроса студентов. N – есть номер фамилии студента в аудиторном журнале.
Решение:
N = 21, n = N + 10 = 21 + 10 = 31
М = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31}.
Перестановка n элементов множества М : Pn = PN + 10 = P31 .
Ответ: PN + 10 = P31 .
Задача №2.21
В каталоге библиотеки приведены наименования N + 100 различных журналов. Найти число способов выбора пяти попарно различных журналов.
Решение:
N = 21, n = N + 100 = 121, r = 5.
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 121}.
__n!_____
Число сочетаний из n элементов множества по r : С rn = r! · (n – r)!
____121!____
С rN + 100 = С 5121 = 5! · (121 – 5)! = 216071394.
Ответ: С rN + 100 = С 5121 = 216071394.
Задача №3.21
У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если ему дают три имени, а общее число имен равно N + 300? Способы отличаются лишь порядком имен, считаются различными.
Решение:
N = 21, n = N + 300 = 21 + 300 = 321.
Число размещений без повторов из n элементов по r :
__ n!__
Arn = n ∙ (n – 1) ∙ (n – 2) ∙ …∙ (n – r + 1) = (n – r)!
___321!__ _321!_
A3N + 300 = A3321 = (321 - 3)! = 300!
_321!_
Ответ: A3N + 300 = A3321 = 300!
Задача №4.21
Сколькими способами можно выбрать 7 делегатов на конференцию от коллектива в N + 200 человек?
Решение:
N = 21, n = N + 200 = 221, r = 7.
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 221}.
__n!_____
Число сочетаний из n элементов множества по r : С rn = r! · (n – r)!
____221!____
С rN + 200 = С 7221 = 7! · (221 – 7)! .
____221!____
Ответ: С rN + 200 = С 7221 = 7! · (221 – 7)! .
Задача №5.21
Группа из N + 10 студентов должна сдать 5 экзаменов. Каково число возможных расписаний сдачи экзаменов?
Решение:
N = 21, N + 10 = 31, n = 5.
Число перестановок без повторов равно Рn = n! = 5! = 120.
Ответ: Рn = n! = 5! = 120.
Задача №6.21
В районе имеется N + 10 памятников. Время позволяет осмотреть только 3 из них. Укажите число возможных маршрутов. Порядок прохождения маршрутов существенен.
Решение:
N = 21, n = N + 10 = 31, r = 3.
Число размещений без повторов из n элементов по r :
__ n!__ __31!__
Arn = n ∙ (n – 1) ∙ (n – 2) ∙ …∙ (n – r + 1) = (n – r)! = (31 – 3)! = 32736.
__ n!__ __31!__
Ответ: Arn = (n – r)! = (31 – 3)! = 32736.
Задача №7.21
Студентам положено на выбор N + 5 гуманитарных предметов. Сколькими способами студент может выбрать 3 из них?
Решение:
N = 21, n = N + 5 = 26, r = 3.
Число размещений без повторов из n элементов по r :
__ n!__ __26!__
Arn = n ∙ (n – 1) ∙ (n – 2) ∙ …∙ (n – r + 1) = (n – r)! = (26 – 3)! = 19656.
__ n!__ __26!__
Ответ: Arn = (n – r)! = (26 – 3)! = 19656.
Задача №8.21
Сколькими способами можно рассадить N + 20 студентов (по одному за каждый компьютер) в дисплейном классе, оснащенном 20 компьютерами? Номера компьютеров существенны.
Решение:
N = 21, n = N + 20 = 41, r = 20.
Число размещений без повторов из n элементов по r :
__ n!__ __41!__
Arn = n ∙ (n – 1) ∙ (n – 2) ∙ …∙ (n – r + 1) = (n – r)! = (41 – 20)! .
__ n!__ __41!__
Ответ: Arn = (n – r)! = (41 – 20)! .
Задача №9.21
В соревновании участвуют N +15 спортсменов. Укажите число вариантов очередности их выступления.
Решение:
N = 21, n = N + 15 = 21 + 15 = 36.
М = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36}.
Перестановка n элементов множества М : Pn = PN + 15 = P36 .
Ответ: PN + 15 = P36.
Задача №10.21
В отделе работает N + 12 сотрудников, которые могут уходить в отпуск только по одному в месяц. Сколько вариантов распределения отпусков в году возможно?
Решение:
N = 21, n = N + 12 = 33, r = 12.
Число размещений без повторов из n элементов по r :
__ n!__ __33!__
Arn = n ∙ (n – 1) ∙ (n – 2) ∙ …∙ (n – r + 1) = (n – r)! = (33 – 12)! .
__ n!__ __33!__
Ответ: Arn = (n – r)! = (33 – 12)! .
Задача №11.21
В киоске имеется N + 10 сортов мороженого одинаковой стоимости. Сколькими способами можно купить 3 порции мороженого попарно различного сорта?
Решение:
N = 21, n = N + 10 = 31, r = 3.
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 31}.
__n!_____
Число сочетаний из n элементов множества по r : С rn = r! · (n – r)! .
____31!____
С rN + 10 = С 331 = 3! · (31 – 3)! = 5456.
Ответ: С rN + 10 = С 331 = 5456.
Задача №12.21
Группа из N + 23 человека должна выполнить лабораторную работу. Сколькими способами можно разбить группу на бригады по 3 человека в бригаде?
Решение:
N = 21, n = N + 23 = 44, r = 3.
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 44}.
__n!_____
Число сочетаний из n элементов множества по r : С rn = r! · (n – r)!
____44!____
С rN + 23 = С 344 = 3! · (44 – 3)! = 15180.
Ответ: С rN + 23 = С 344 = 15180.
Задача №13.21
Правило суммы и правило произведения.
Составить график отпусков на январь, февраль, март. В январе в отпуск должно уйти r = N + 10 человек, в феврале s = N + 8, в марте t = N + 15. Сколькими способами можно составить график, если в отделе n = 150 человек?
Решение:
N = 21, r = N + 10 = 31, s = N + 8 = 29, t = N + 15 = 36,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 150}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!_____ __ (n – r)!____ __ (n – r – s)! ___
С rn = r! · (n – r)! , С sn – r = s! · (n – r – s)! , С tn – r – s = t! · (n – r – s – t)! .
_____150!_____ ____(150 – 31)!_____
С rn ∙ С sn – r ∙ С tn – r – s = 31! ∙ (150 – 31)! ∙ 31! ∙ (150 – 31 – 29)! ∙
____(150 – 31 – 29)!_____ __150!__ __117!__ __86!__
∙36! ∙ (150 – 31 – 29 – 36)! = 31! ∙ 117! ∙ 29! ∙ 86! ∙ 36! ∙ 48! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
___ n!____ __ (n – r)!____
С rn ∙ С sn – r = С sn ∙ С sn – s ↔ r! · (n – r)! ∙ s! · (n – r – s)! =
___n!____ ____(n – s)!__ _____ n!______ _____ n!______
s! · (n – s)! ∙ r! · (n – s – r)! ↔ r! s! · (n – r – s)! = s! r! · (n – s – r)! .
__150!__ __117!__ __86!__
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 31! ∙ 117! ∙ 29! ∙ 86! ∙ 36! ∙ 48! .
Задача №14.21
Правило суммы и правило произведения.
Сколькими способами путем выбора из n = N + 100 человек можно составить комиссию, состоящую из r = 1 председателя, s = 3 заместителей и
t = 5 рядовых членов?
Решение:
N = 21, n = N + 100 = 121, r = 1, s = 3, t = 5,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 121}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!_____ __ (n – r)!____ __ (n – r – s)! ___
С rn = r! · (n – r)! , С sn – r = s! · (n – r – s)! , С tn – r – s = t! · (n – r – s – t)! .
____121!____ ____(121 – 1)!___
С rn ∙ С sn – r ∙ С tn – r – s = 1! ∙ (121 – 1)! ∙ 3! ∙ (121 – 1 – 3)! ∙
____(121 – 1 – 3)!___ __121!__ __120!__ __117!__
∙5! ∙ (121 – 1 – 3 – 5)! = 1! ∙ 120! ∙ 3! ∙ 117! ∙ 5! ∙ 112! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
___ n!____ __ (n – r)!____
С rn ∙ С sn – r = С sn ∙ С sn – s ↔ r! · (n – r)! ∙ s! · (n – r – s)! =
___n!____ ____(n – s)!__ _____ n!______ _____ n!______
s! · (n – s)! ∙ r! · (n – s – r)! ↔ r! s! · (n – r – s)! = s! r! · (n – s – r)! .
__121!__ __120!__ __117!__
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 1! ∙ 120! ∙ 3! ∙ 117! ∙ 5! ∙ 112! .
Задача №15.21
Правило суммы и правило произведения.
Для премирования n = N + 12 сотрудников куплены следующие книги: «Памятники Москвы», r = 3 экземпляра; «Фонтаны Петергофа», s = 4 экземпляра; «Вологодские кружева», t = 5 экземпляров. Сколькими способами можно распределить книги?
Решение:
N = 21, n = N + 12 = 33, r = 3, s = 4 t = 5,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 33}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!_____ __ (n – r)!____ __ (n – r – s)! ___
С rn = r! · (n – r)! , С sn – r = s! · (n – r – s)! , С tn – r – s = t! · (n – r – s – t)! .
____33!____ ____(33 – 3)!___
С rn ∙ С sn – r ∙ С tn – r – s = 3! ∙ (33 – 3)! ∙ 4! ∙ (33 – 3 – 4)! ∙
____(33 – 3 – 4)!___ __33!__ __30!__ __21! __
∙5! ∙ (33 – 3 – 4 – 5)! = 3! ∙ 30! ∙ 4! ∙ 26! ∙ 5! ∙ 21! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
___ n!____ __ (n – r)!____
С rn ∙ С sn – r = С sn ∙ С sn – s ↔ r! · (n – r)! ∙ s! · (n – r – s)! =
___n!____ ____(n – s)!__ _____ n!______ _____ n!______
s! · (n – s)! ∙ r! · (n – s – r)! ↔ r! s! · (n – r – s)! = s! r! · (n – s – r)! .
__33!__ __30! __ __26!__
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 3! ∙ 30! ∙ 4! ∙ 26! ∙ 5! ∙ 21! .
Задача №16.21
Правило суммы и правило произведения.
На n = N + 100 сотрудников выделено 11 путевок: r = 2 в санаторий «Дорохово»; s = 5 в санаторий «Энергия»; t = 4 в санаторий «Звенигород». Сколькими способами можно распределить путевки?
Решение:
N = 21, n = N + 100 = 121, r = 2, s = 5, t = 4,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 121}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!_____ __ (n – r)!____ __ (n – r – s)! ___
С rn = r! · (n – r)! , С sn – r = s! · (n – r – s)! , С tn – r – s = t! · (n – r – s – t)! .
____121!____ ____(121 – 2)!___
С rn ∙ С sn – r ∙ С tn – r – s = 2! ∙ (121 – 2)! ∙ 5! ∙ (121 – 2 – 5)! ∙
____(121 – 2 – 5)!___ __121!__ __119!__ __114!__
∙4! ∙ (121 – 2 – 5 – 4)! = 2! ∙ 119! ∙ 5! ∙ 114! ∙ 4! ∙ 110! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
___ n!____ __ (n – r)!____
С rn ∙ С sn – r = С sn ∙ С sn – s ↔ r! · (n – r)! ∙ s! · (n – r – s)! =
___n!____ ____(n – s)!__ _____ n!______ _____ n!______
s! · (n – s)! ∙ r! · (n – s – r)! ↔ r! s! · (n – r – s)! = s! r! · (n – s – r)! .
__121!__ __119!__ __114!__
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 2! ∙ 119! ∙ 5! ∙ 114! ∙ 4! ∙ 110! .
Задача №17.21
Правило суммы и правило произведения.
Для охраны здания требуется наряд их 8 человек. r = 2 из них для охраны входа, s = 2 для охраны сейфа и архива, t = 4 для патрулирования. Сколькими способами можно сформировать такой наряд, имея n = N + 20 человек?
Решение:
N = 21, n = N + 20 = 41, r = 2, s = 2, t = 4,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 41}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!_____ __ (n – r)!____ __ (n – r – s)! ___
С rn = r! · (n – r)! , С sn – r = s! · (n – r – s)! , С tn – r – s = t! · (n – r – s – t)! .
____41!____ ____(41 – 2)!___
С rn ∙ С sn – r ∙ С tn – r – s = 2! ∙ (41 – 2)! ∙ 2! ∙ (41 – 2 – 2)! ∙
____(41 – 2 – 2)!___ __41!__ __39!__ __37!__
∙4! ∙ (41 – 2 – 2 – 4)! = 2! ∙ 39! ∙ 2! ∙ 37! ∙ 4! ∙ 33! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
___ n!____ __ (n – r)!____
С rn ∙ С sn – r = С sn ∙ С sn – s ↔ r! · (n – r)! ∙ s! · (n – r – s)! =
___n!____ ____(n – s)!__ _____ n!______ _____ n!______
s! · (n – s)! ∙ r! · (n – s – r)! ↔ r! s! · (n – r – s)! = s! r! · (n – s – r)! .
__41!__ __39!__ __37!__
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 2! ∙ 39! ∙ 2! ∙ 37! ∙ 4! ∙ 33! .
Задача №18.21
Правило суммы и правило произведения.
В удержании n = N + 300 сотрудников. Сколько вариантов назначения администрации возможно, если администрация должна состоять из r = 1 директора, s = 1 главного инженера и t = 3 заместителей?
Решение:
N = 21, n = N + 300 = 321, r = 1, s = 1, t = 3,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 321}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!_____ __ (n – r)!____ __ (n – r – s)! ___
С rn = r! · (n – r)! , С sn – r = s! · (n – r – s)! , С tn – r – s = t! · (n – r – s – t)! .
____321!____ ____(321 – 1)!___
С rn ∙ С sn – r ∙ С tn – r – s = 1! ∙ (321 – 1)! ∙ 1! ∙ (321 – 1 – 1)! ∙
____(321 – 1 – 1)!___ __321!__ __320!__ __319!__
∙3! ∙ (321 – 1 – 1 – 3)! = 1! ∙ 320! ∙ 1! ∙ 319! ∙ 3! ∙ 316! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
___ n!____ __ (n – r)!____
С rn ∙ С sn – r = С sn ∙ С sn – s ↔ r! · (n – r)! ∙ s! · (n – r – s)! =
___n!____ ____(n – s)!__ _____ n!______ _____ n!______
s! · (n – s)! ∙ r! · (n – s – r)! ↔ r! s! · (n – r – s)! = s! r! · (n – s – r)! .
__321!__ __320!__ __319!__
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 1! ∙ 320! ∙ 1! ∙ 319! ∙ 3! ∙ 316! .
Задача №19.21
Правило суммы и правило произведения.
Для охраны здания надо выделить наряд из 8 человек: r = 2 для охраны входа, по одному: s = 1+ 1 = 2 для охраны сейфа и архива (с учетом распределения обязанностей), t = 4 для патрулирования. Сколькими способами можно выделить такой наряд, имея в расположении n = N + 20 человек.
Решение:
N = 21, n = N + 20 = 41, r = 2, s = 2, t = 4,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 41}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!___ _ (n – r)!__ _ (n – r – s)! _
А rn = (n – r)! , А sn – r = (n – r – s)! , А tn – r – s = (n – r – s – t)! .
__41!___ __(41 – 2)!__
А rn ∙ А sn – r ∙ А tn – r – s = (41 – 2)! ∙ (41 – 2 – 2)! ∙
__(41 – 2 – 2)!__ _41!_ _39!_ _37!_
∙(41 – 2 – 2 – 4)! = 39! ∙ 37! ∙ 33! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
__ n!__ _ (n – r)!__
А rn ∙ А sn – r = А sn ∙ А sn – s ↔ (n – r)! ∙ (n – r – s)! =
___n!__ _(n – s)!__ __ n!____ ___ n!___
= (n – s)! ∙ (n – s – r)! ↔ (n – r – s)! = (n – s – r)! .
_41!_ _39!_ _37!_
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 39! ∙ 37! ∙ 33! .
Задача №20.21
Правило суммы и правило произведения.
Сколькими способами можно распределить 6 именных стипендий между N + 100 отличниками, если имеется 1 стипендия имени М1, 2 стипендии имени М2, 3 стипендии имени М3.
Решение:
N = 21, n = N + 100 = 121, r = М1 = 1, s = М2 = 2, t = М3 = 3,
M = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 121}.
Множество М разбито на 3 непересекающихся подмножества M1 , M2 , M3 :
|M| = |M1| + |M2| + |M3|, тогда С rn ∙ С sn – r ∙ С tn – r – s .
__n!___ _ (n – r)!__ _ (n – r – s)! _
А rn = (n – r)! , А sn – r = (n – r – s)! , А tn – r – s = (n – r – s – t)! .
__121!___ __(121 – 1)!__
А rn ∙ А sn – r ∙ А tn – r – s = (121 – 1)! ∙ (121 – 1 – 2)! ∙
__(121 – 1 – 2)!__ _121!_ _120!_ _118!_
∙(121 – 1 – 2 – 3)! = 120! ∙ 118! ∙ 115! .
Число способов составления графика не зависит от порядка месяцев, ибо справедлива следующая последовательность равенств:
__ n!__ _ (n – r)!__
А rn ∙ А sn – r = А sn ∙ А sn – s ↔ (n – r)! ∙ (n – r – s)! =
___n!__ _(n – s)!__ __ n!____ ___ n!___
= (n – s)! ∙ (n – s – r)! ↔ (n – r – s)! = (n – s – r)! .
_121!_ _120!_ _118!_
Ответ: С rn ∙ С sn – r ∙ С tn – r – s = 120! ∙ 118! ∙ 115! .
Задача №21.21
Разные задачи.
В некотором языке программирования имя переменной может состоять из n = N + 7 десятичных цифр и латинских букв, причем имя переменной может быть любой последовательностью из букв и цифр (с повторами символов) любой длины l, 1 ≤ l ≤ n. Сколько различных имен переменных возможно в этом языке?
Решение:
N = 21, n = N + 7 = 28, 1 ≤ l ≤ n.
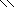
Число размещений с повтором: Аnn = nn
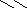
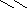
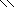
Число различных имен переменных: Аn – n+1n ∙ Аn – n+2n ∙ Аn – n+3n ∙ … ∙ Аnn =
nn – n+1 ∙ nn – n+2 ∙ nn – n+3 ∙ … ∙ nn = n1 ∙ n2 ∙ n3 ∙ … ∙ n28 .
Ответ: n1 ∙ n2 ∙ n3 ∙ … ∙ n28.
Задача №22.21
Разные задачи.
N + 5 мальчиков и N + 5 девочек с попарно различными именами должны быть рассажены в ряд. Сколькими способами можно это сделать, если:
а) все мальчики должны сидеть на самых левых местах;
б) никакие два мальчика не должны сидеть рядом;
в) Маша и Петя должны сидеть вместе.
Решение:
N = 21, N + 5 = 26.
а) все мальчики должны сидеть на самых левых местах: для этого рассадим всех мальчиков строго на левые места ряда: м м м… м, а девочек рядом с мальчиками: д д д… д, PN + 5 ∙ PN + 5 = P26 ∙ P26.
б) никакие два мальчика не должны сидеть рядом: для этого, мы рассадим всех мальчиков со всеми девочками: мд мд мд…мд или дм дм дм…дм,
2 ∙ PN + 5 ∙ PN + 5 = 2 ∙ P26 ∙ P26 .
в) Маша и Петя должны сидеть вместе: Маша и Петя, а так же Петя и Маша среди всех позиций мальчиков с девочками 2 ∙ PN + 5 ∙ PN + 5 могут занимать позиции от 0 до 2N + 8. Это P(2N + 8) ∙2(2N + 9) = P164 .
Ответ: а) PN + 5 ∙ PN + 5 = P28 ∙ P28 , б) 2 ∙ PN + 5 ∙ PN + 5 = 2 ∙ P26∙ P26 ,
в) P(2N + 8) ∙2(2N + 9) = P164 .
Задача №23.21
Разные задачи.
Сколькими способами можно расставить N + 10 мальчиков и N + 5 девочек так, чтобы никакие две девочки не стояли рядом:
а) в линию?
б) в круг?
Решение:
N = 21, N + 10 = 31, N + 5 = 26.
а) в линию: PN + 10 ∙ A(N + 10)+2 N+5 = P31 ∙ A33 26 ,
б) в круг: PN + 10 ∙ AN + 10 N+5 = P31 ∙ A31 26 .
Ответ: а) в линию: PN + 10 ∙ A(N + 10)+2 N+5 = P31 ∙ A3326 ,
б) в круг: PN + 10 ∙ AN + 10 N+5 = P31 ∙ A31 26 .
Задача №24.21
Разные задачи.
Сколькими способами можно упорядочить N + 30 символов так, чтобы между символами N и N + 1 стояло ровно 5 других символов.
Решение:
N = 21, N + 1 = 22, N + 30 = 51, N + 28 = 49.
Числа множества {1, 2, …, N + 30} – {N, N + 1} могут занимать позиции от 1 до N + 28, это РN+30 возможностей их перестановок. Число N может занимать позиции от 0 до N + 22, это N + 23 возможностей его положения. Третий ряд позиций ниже это соответствующие позиции числа N + 1, когда между N и N + 1 стоят пять других чисел. Число N может стоять раньше
N + 1, это еще N + 21 возможностей их положения. По правилу умножения это
P(N + 28) ∙2(N + 23) = P143 возможностей.
1 2 3 4 5 … N + 23 N + 24 N + 25 N + 26 N + 27 N + 28
0 1 2 3 4 5 6 … N + 22
6 … N + 23 N + 24 N + 25 N + 26 N + 27 N + 28
Ответ: P(N + 28) ∙2(N + 21) = P143 .
Задача №25.21
Разные задачи.
а) Сколькими способами могут быть упорядочены буквы в слове
p a r a l l e l o g r a m с приписанной к нему вашей фамилией, записанной в латинице?
б) Сколькими способами они могут быть упорядочены, если буквы l не должны стоять рядом?
Решение:
p a r a l l e l o g r a m, fadeev.
1. Слово w = p a r a l l e l o g r a m без приписанной к нему фамилии состоит из букв p, a, r, l, e, o, g, m, число повторений которых в слове соответственно равны 1, 3, 2, 3, 1, 1, 1, 1.
а) Число способов упорядочения равно:
_______13!_______
К1 = Р13 (1, 3, 2, 3, 1, 1, 1, 1) = 1! 3! 2! 3! 1! 1! 1! 1! .
б) Слово p a r a e o g r a m есть слово w без буквы l. Оно состоит из семи букв p, a, r, e, o, g, m, число повторений которых в слове соответственно равны 1, 3, 2, 1, 1, 1, 1. Число перестановок этих семи букв
_____10!_______
К2 = Р10 (1, 3, 2, 1, 1, 1, 1) = 1! 3! 2! 1! 1! 1! 1! .
Три буквы l должны быть разделены в слове p a r a e o g r a m хотя бы одной буквой. Ниже указано слово (строка 1), позиции его букв (строка 2) и позиции между ними (строка 3). Буквы l могут занимать любые три позиции. Это С113 возможностей. По правилу умножения число способов упорядочения равно К2 ∙ С113 .
p a r a e o g r a m буквы слова p a r a l l e l o g r a m без l
1 2 3 4 5 6 7 8 9 10 их позиции
0 1 2 3 4 5 6 7 8 9 10 позиции между ними
2. Слово w = p a r a l l e l o g r a m fadeev с приписанной к нему фамилией состоит из букв p, a, r, l, e, o, g, m, f, a, d, v, число повторений которых в слове соответственно равны 1, 5, 2, 4, 1, 2, 1, 1, 1, 2, 1, 1.
а) Число способов упорядочения равно:
___________22!____________
К1 = Р22 (1, 5, 2, 4, 1, 2, 1, 1, 1, 2, 1, 1) = 1! 5! 2! 4! 1! 2! 1! 1! 1! 2! 1! 1! .
б) Слово p a r a e o g r a m fadeev есть слово w без буквы l. Оно состоит из одиннадцати букв p, a, r, e, o, g, m, f, a, d, v, число повторений которых в слове соответственно равны 1, 5, 2, 1, 2, 1, 1, 1, 2, 1, 1. Число перестановок этих семи букв
__________18!___________
К2 = Р18 (1, 5, 2, 1, 2, 1, 1, 1, 2, 1, 1) = 1! 5! 2! 1! 2! 1! 1! 1! 2! 1! 1! .
Четыре буквы l должны быть разделены в слове p a r a e o g r a m fadeev хотя бы одной буквой. Ниже указано слово (строка 1), позиции его букв (строка 2) и позиции между ними (строка 3). Буквы l могут занимать любые три позиции. Это С113 возможностей. По правилу умножения число способов упорядочения равно К2 ∙ С194 .
p a r a e o g r a m fadeev буквы слова paraeogramfadeev без l
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 их позиции
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 позиции между ними
Задача 26.21
Пусть повторения цифр запрещены. Сколько N + 4 – разрядных чисел могут быть сформированы из цифр 2, 3, 5, 6, 8, 9, если:
а) ограничений нет;
б) числа меньше 500;
в) числа четные;
г) числа нечетные;
д) числа делятся на 3;
е) числа делятся либо только на 2, либо только на 3;
ж) числа делятся на 2 или на 3;
з) числа делятся одновременно на 2 и на 3.
Решение:
N = 21, N + 4 = 21 + 4 = 25.
а) n = A64 .
б) числа начинаются с 2 или с 3. n = 2 ∙ A53 .
в) числа четные заканчиваются на 2, 6, 8. n = 3 ∙ A53 .
г) числа нечетные заканчиваются на 3, 5, 9. n = 3 ∙ A53 .
д) пусть знак
: означает
«делится на». Число
: 3, если сумма
его цифр делится на 3. Это любая перестановка
чисел 2, 5, 8, а,
где а
{3,
6, 9}.
n = 3 ∙ P4 .
з) пусть знак с(
: m)
означает число (cardinality)
чисел, которые
: m.
Пусть
знаки & и
означают «и» и «или» соответственно.
Числа, которые : 3& :2 получается, если
из чисел, которые :3, оставим лишь четные
числа, то есть заканчивающиеся на 6, 8,
2. Это числа видаabc6,
def8,
ghi2,
jkl2,
mno2,
где abc,
def,
ghi,
jkl,
mno
есть любая перестановка цифр 258, 253, 358,
658, 958 соответственно. Тогда n
= c(:3
& :2) = 5P3
.
ж) n
= c(:3
:2) =с(:3)
+ с(:2)
– с(:3
& :2) = 3∙P4
+ 3∙
A53
– 5∙
P3
.
е) пусть знак
означает «исключающее или». Тогдаn
= c(:3
:2) =с(:3)
+
+ с(:2) – 2∙с(:3 & :2) = 3∙P4 + 3∙ A53 – 2∙5∙ P3 = 3∙P4 + 3∙ A53 – 10∙ P3 .
Задача 26(1).21
Пусть повторения цифр не запрещены. Сколько N + 24 – разрядных чисел могут быть сформированы из цифр 2, 3, 5, 6, 8, 9, если:
а) ограничений нет;
б) числа меньше 5∙10N + 24;
в) числа четные;
г) числа нечетные;
д) числа, имеющие в своей 10-ричной записи N двоек, не имеющих пятерок и восьмерок и делящиеся на 3.
Решение:
N = 21, N + 24 = 21 + 24 = 45.
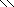
а) A6N+24 = 6N + 24 =645 .
б) числа меньше 5∙10N + 24 это числа,начинающиеся с 2 и 3. Их число есть
2 ∙ 6N + 23 =2 ∙ 644 .
в) числа четные заканчиваются на 2, 6, 8. Их число равно
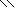
n = 3 ∙ A6N+23 = 3 ∙ 6N + 23 =3 ∙ 644 .
г) числа нечетные заканчиваются на 3, 5, 9. Их число равно
n = 3 ∙ A6N+23 = 3 ∙ 6N + 23 =3 ∙ 644 .
д) число х : 3, если сумма его цифр :3. Сгруппируем сумму цифр в х в две суммы S1 + S2 , где S1 есть сумма двоек в х, и S2 есть сумма всех троек, шестерок, девяток в х. S2 : 3. Пусть в х N двоек, i1 троек, i2 шестерок, i3 девяток, причем i1 + i2 + i3 = N + 24 – N = 24. Число чисел с N двойками, i1 тройками, i2 шестерками, i3 девятками есть число перестановок из N + 24 цифр 2, 3, 6, 9 спецификации (N, i1, i2, i3), причем N + i1 + i2 + i3 = N + 24. Их
_(N + 24)!_ ___47!____
число равно РN + 24 (N, i1, i2, i3) = N! i1! i2! i3! = 21! i1! i2! i3! .
Ответ: Если сумма 2N всех двоек в х не кратна 3, то число обсуждаемых чисел равно нулю. Если 2N : 3, то число обсуждаемых чисел равно
_(N + 24)!_ ___45!____
∑ РN + 24 = ∑ N! i1! i2! i3! = ∑ 21! i1! i2! i3! .
i1 + i2 + i3 = 24 i1 + i2 + i3 = 24 i1 + i2 + i3 = 24
Задача №27.21
Разные задачи.
В анкете предлагается N + 15 вопросов, на которые можно ответить «да», «нет», «затрудняюсь ответить». Сколькими способами можно ответить на вопросы анкеты?
Решение:
N
= 21, n
= N
+ 15 = 36, r
= 3.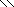
Число размещений с повтором: Аrn = r n = 3N + 15 = 336 .
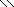
Ответ: Аrn = r n = 3N + 15 = 336 .
Задача №28.21
Разные задачи.
Палиндром это слово, которое одинаково читается как слева направо, так и справа налево. Сколько палиндромов из N + 7 букв можно составить в латинице, не заботясь о смысле слова?
Решение:
N
= 21, n
= N
+ 7 = 28, r
= 26.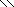
Число размещений с повтором: Аrn = r n = 26N + 7 = 2628 , но поскольку слово палиндром читается как слева направо, так и справа налево одинаково, то
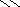
Аrn/2 = r n /2= 26(N + 7)/2 = 2615 .
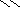
Ответ: Аrn/2 = r n /2= 26(N + 7)/2 = 2615.
Задача 29.21
Сколько шестисимвольных слов можно сформировать из N + 26 букв и цифр, если:
а) первые два символа есть буквы, а следующие четыре – цифры;
б) в слове может быть только две буквы, которые не должны стоять в слове рядом.
Решение:
N = 21, N + 26 = 47, r = 26.
а) первые два символа есть буквы, а следующие четыре – цифры: А262 ∙104.
б) в слове может быть только две буквы, которые не должны стоять в слове рядом: 10N + 24 ∙ C2N + 25 ∙ 262 = 1045 ∙ C246 ∙ 262.
Ответ: а) А262 ∙104 , б) 10N + 24 ∙ C2N + 25 ∙ 262 = 1045 ∙ C246 ∙ 262
Задача 30.21
Найти число положительных натуральных чисел, не больших 1000+2∙N+1 и
1) не делящихся ни на одно из чисел 3, 5, 7, 11, 13;
2) делящихся в точности на два числа из {3, 5, 7, 11, 13};
3) делящихся на не менее чем два числа из {3, 5, 7, 11, 13}.
N есть номер фамилии студента в аудиторном журнале. Использовать формулу включений и исключений.
Решение:
N = 21, 1000 + 2∙N + 1 = 1047.
Используем формулы включений и исключений для числа предметов N и числа свойств n.
N(0) = ∑ (−1)r ∑ N(i1, i2, …, ir);
r = 0 1≤ i1 < i2 <…< ir ≤n
n – k
N = k = ∑ (−1) j C jk + j ∑ N(i1, i2, …, ik + j);
j = 0 1≤ i1 < i2 <…< ik + j ≤n
n – k
N ≥ k = ∑ (−1) j C k – 1 k – 1 + j ∑ N(i1, i2, …, ik + j);
j = 0 1≤ i1 < i2 <…< ik + j ≤n
Свойство 1: число k делится на 3.
Свойство 2: число k делится на 5.
Свойство 3: число k делится на 7.
Свойство 4: число k делится на 11.
Свойство 5: число k делится на 13.
Пусть M есть множество чисел между 1 и N, обладающих одним из перечисленных свойств или их сочетанием (табл. 1).
|
Свойство |
Множество М чисел |
Число чисел в М |
|
1 2 3 4 5 1, 2 1, 3 1, 4 1, 5 2, 3 2, 4 2, 5 3, 4 3, 5 4, 5 1, 2, 3 1, 2, 4 1, 2, 5 1, 3, 4 1, 3, 5 1, 4, 5 2, 3, 4 2, 3, 5 2, 4, 5 3, 4, 5 1, 2, 3, 4 1, 2, 4, 5 1, 2, 3, 5 1, 3, 4, 5 2, 3, 4, 5 |
{3k: k = 1, 2,…, 349} {5k: k = 1, 2,…, 209} {7k: k = 1, 2,…, 149} {11k: k = 1, 2,…, 95} {13k: k = 1, 2,…, 80} {15k: k = 1, 2,…, 69} {21k: k = 1, 2,…, 49} {33k: k = 1, 2,…, 31} {39k: k = 1, 2,…, 26} {35k: k = 1, 2,…, 29} {55k: k = 1, 2,…, 19} {65k: k = 1, 2,…, 16} {77k: k = 1, 2,…, 13} {91k: k = 1, 2,…, 11} {143k: k = 1, 2,…, 7} {105k: k = 1, 2,…, 9} {165k: k = 1, 2,…, 6} {195k: k = 1, 2,…, 5} {231k: k = 1, 2,…, 4} {273k: k = 1, 2,…, 3} {429k: k = 1, 2} {385k: k = 1, 2} {455k: k = 1, 2} {715k: k = 1} {1001k: k = 1} {1155k: k = 0} {2145k: k = 0} {1365k: k = 0} {3003k: k = 0} {5005k: k = 0} |
N(1) = 349 N(2) = 209 N(3) = 149 N(4) = 95 N(5) = 80 N(1, 2) = 69 N(1, 3) = 49 N(1, 4) = 31 N(1, 5) = 26 N(2, 3) = 29 N(2, 4) = 19 N(2, 5) = 16 N(3, 4) = 13 N(3, 5) = 11 N(4, 5) = 7 N(1, 2, 3) = 9 N(1, 2, 4) = 6 N(1, 2, 4) = 5 N(1, 3, 4) = 4 N(1, 3, 5) = 3 N(1, 4, 5) = 2 N(2, 3, 4) = 2 N(2, 3, 5) = 2 N(2, 4, 5) = 1 N(3, 4, 5) = 1 N(1, 2, 3, 4) = 0 N(1, 2, 4, 5) = 0 N(1, 2, 3, 5) = 0 N(1, 3, 4, 5) = 0 N(2, 3, 4, 5) = 0 |
N(0) = 1047 – ∑ N(i) + ∑ N(i, j) – ∑ N(i, j, k) = 1047 – (349 +
1≤ i ≤5 1≤ i < j ≤10 1≤ i < j < k ≤10
+ 209 + 149 + 95 + 80) + (69 + 49 + 31 + 26 + 29 + 19 + 16 + 13 + 11 + 7) – (9 + 6 + 5 + 4 + 3 + 2 + 2 + 2 + 1 + 1) = 400.
5 – 2
N = 2 = ∑ (−1) j C j2 + j ∑ N(i1, i2, …, i2 + j) = ((−1)0 C 02 +
j = 0 1≤ i1 < i2 <…< i2 + j ≤5
+ (−1)1 C 13 + (−1)2 C 24 + (−1)3 C 35) ∑ N(i, j) + (−1)1 C 54 N(1, 2, 3, 4) =
1≤ i < j ≤5
___3!__ ___4! ___ ___5!___
= (1 + (−1) (1!(3 – 1)! + 2!(4 – 2)! + 3!(5 – 3)! ))+(69 + 49 + 31 + 26 + 29 + 19 +
+ 16 + 13 + 11 + 7) =(1 + (−1)(3 + 6 + 10)) + 270 = 252.
5 – 2
N ≥ 2 = ∑ (−1) j C j2 – 1 + j ∑ N(i1, i2, …, i2 + j) = ((−1)0 C 01 +
j = 0 1≤ i1 < i2 <…< i2 + j ≤5
+ (−1)1 C 12 + (−1)2 C 23 + (−1)3 C 34) ∑ N(i, j) + (−1)1 C 53 N(1, 2, 3, 4) =
1≤ i < j≤5
___2!__ ___3! ___ ___4!___
= (1 + (−1) (1!(2 – 1)! + 2!(3 – 2)! + 3!(4 – 3)! ))+(69 + 49 + 31 + 26 + 29 + 19 +
+ 16 + 13 + 11 + 7) =(1 + (−1)(2 + 3 + 4)) + 270 = 262.
Московский энергетический институт
(технический университет)