
- •Курсовая работа по курсу «Комбинаторика»
- •Курсовая работа по курсу «Модулярная арифметика»
- •Курсовая работа по курсу «Графы»
- •2 4 E3
- •Алгоритм построения совершенного паросочетания для двудольного графа.
- •X1 y1
- •X1 y1 Шаг 4.
- •Алгоритм построения совершенного паросочетания в полном нагруженном двудольном графе.
- •X1 y1 x1 0 3 4 3
- •4X1 y1 0 x1 x1 x2
- •7 X2 y2 0 y3 y3
- •8 X3 y3 0
- •7 X4 y4 0
- •3X1 y1 0 x2 x1 x2 x3
- •6 X2 y2 0 y2 y3 y2
- •8 X3 y3 1
- •7 X4 y4 0
- •3X1 y1 0 x3 x1 x2 x3
- •3X1 y1 0 x4 x1 x1 x3 x4
- •6 X2 y2 0 y2 y1 y4 y1
- •7 X3 y3 1 x1
- •6 X4 y4 0 y4
- •3 X1 y1 0
- •6 X2 y2 0
- •7 X3 y3 1
- •6 X4 y4 0
- •Приложение
2 4 E3







e11
e13
e14
e4
e12
e15
e16

1
5


e9



e5
e8
e10

6


e6

8

e7
7
3
e2
e1

2
4




e3







e11
e13
e14

e1
e4
e12
e15
e16

1
5


e9


e5
e8

6


e6

8

e7
7
3
e1
e2

2
4










e11
e13
e14

e1
e4
e12
e15
e16

1
5


e9


e5
e8
e10

6


e6

8

e7
7
3
e1
e2

2
4



e3






e11
e13
e14

e1
e4
e12
e16

1
5


e9


e5
e8
e10

6


e6

8

e7
7
3
e1
e2

2
4




e3







e11
e13
e14

e1
e4
e12
e15
e16

1
5


e9


e5
e10

6


e6

8

e7
7
3
e1
e2

2
4




e3







e11
e13
e14

e1
e4
e12
e15
e16

1
5


e9


e5
e8
e10

6


8

e7
7
3
e1
e2

2
4



e3







e11
e14

e1
e4
e12
e15
e16

1
5


e9


e5
e8
e10

6


e6

8

e7
7
3
e1
e2

2
4




e3







e11
e13
e14

e1
e4
e12
e15
e16

1
5




e5
e8
e10

6


e6

8

e7
7
Матричная теорема о деревьях (Кирхгоф).
Пусть граф G = (V, E) имеет множество вершин V = {v1,…,vp} и ребер Е. Пусть А есть матрица смежности (соседства вершин) графа G, M есть матрица, полученная из матрицы −А заменой элемента i главной диагонали на степень вершины vi, то есть на число ребер, принадлежащих вершине vi.
Стягивающее дерево графа G есть наименьшее по числу ребер подграф-дерево графа G, соединяющее все вершины в G.
Все алгебраические дополнения матрицы M равны между собой и их общее значение равно числу стягивающих деревьев (каркасов) графа G.
Для графа G вычисления дают следующее:
Матрица смежностей: M = − A:
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
┌ ┐
┌
┐
1 0 1 0 1 1 1 0 1 1 4 -1 0 -1 -1 -1 0 1
2 1 0 1 1 0 0 1 0 2 -1 4 -1 -1 0 0 -1 4
3 0 1 0 1 1 0 1 1 3 0 -1 4 -1 -1 0 -1 0
А = 4 1 1 1 0 1 1 1 0 , M = 4 -1 -1 -1 6 -1 -1 -1 1,
5 1 0 1 1 0 1 0 0 5 -1 0 -1 -1 4 -1 0 0
6 1 0 0 1 1 0 1 1 6 -1 0 0 -1 -1 4 -1 1
7 0 1 1 1 0 1 0 1 7 0 -1 -1 -1 0 -1 4 1
8└ 1 1 1 0 1 1 1 0 ┘ 8 └ -1 0 -1 -1 4 -1 0 1 ┘
┌
┐
4 -1 0 -1 -1 0
-1 4 -1 0 0 -1
A44 = (−1)4+4 0 -1 4 -1 0 -1 = 1543.
-1 0 -1 4 -1 0
-1 0 0 -1 4 -1
0 -1 -1 0 -1 4
└ ┘
Ответ: Фундаментальная система циклов: {С1, С2, С3, С4, С5, С6, С7, С8, С9};
Множество хорд: H = {е1, е10, е3, е15, е8, е6, е13, е9, е4};
Все
фундаментальные сечения (разрезы): H![]() {(2,
3)}, H
{(2,
3)}, H![]() {(5,
6)}, H
{(5,
6)}, H![]() {(2,
7)}, H
{(2,
7)}, H![]() {(1, 5)}, H
{(1, 5)}, H![]() {(4, 6)}, H
{(4, 6)}, H![]() {(4, 7)};
{(4, 7)};
Число каркасов данного графа det[M] = 1543.
Задание 5.21
В ненагруженном графе G из задачи 1 с помощью алгоритма надстраивания ребер найти каркас и соответствующее множество хорд, фундаментальную систему циклов, все фундаментальные сечения (разрезы).
G=(V,E)=(V={1,2,3,4,5,6,7,8,9}, E={(1,8),(1,9),(2,5),(2,9),(3,5),(3,6),(3,7),(3,9), (4,5),(4,9),(5,6),(7,9),(8,9)}

Решение:
Каркас графа G можно получить, последовательно надстраивая ребрами из G произвольно взятое из G ребро до дерева, являющегося каркасом. При этом надстройку каждый раз следует выполнять, избегая появления циклов.
Исходим из ребра (4,9). Последовательное его расширение ребрами приводит нас к каркасу (стягивающему дереву).
T={(4,9),(1,9),(8,9),(2,9),(7,9),(3,7),(3,5),(5,6)}

Множество хорд
H=E-T={(1,8),(2,5),(3,6),(3,9), (4,5)}
Последовательно возвращаем в каркас по одной хорде и получаем фундаментальную систему из шести циклов:
С1=1981, С2=2917352, С3=3563, С4=39253, С5=54925.
Всякий фундаментальный разрез составят хорды плюс одно произвольное ребро каркаса. Все фундаментальные разрезы:
H {(4,9)},
H
{(4,9)},
H {(1,9)},
H
{(1,9)},
H {(8,9)},
H
{(8,9)},
H {(2,9)},
H
{(2,9)},
H {(7,9)},
H
{(7,9)},
H {(3,7)},
H
{(3,7)},
H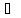 {(3,5)},
H
{(3,5)},
H {(5,6)}.
{(5,6)}.
Задание 6.21
В нагруженном графе G из задачи 1 найти кратчайший (наименьший по весу) каркас и соответствующее множество хорд, фундаментальную систему циклов, все фундаментальные сечения (разрезы). Вес wij неориентированного ребра (vi,vj) с i<j равен N(i2+j2)+ i2+j2 +i+j по модулю 10 (остаток от деления wij на 10). N есть номер варианта (N=21).
G=(V,E)=(V={1,2,3,4,5,6,7,8,9}, E={(1,8,9),(1,9,6),(2,5,2),(2,9,1),(3,5,0),(3,6,9),(3,7,4),(3,9,2), (4,5,7),(4,9,9),(5,6,9),(7,9,6),(8,9,7)}

Решение:
Если граф G является нагруженным (каждому ребру графа G приписано некоторое неотрицательное число-вес ребра, его стоимость), то наименьший каркас (с наименьшей суммой весов ребер) можно получить, последовательно надстраивая ребрами из G произвольно взятое из G ребро с наименьшим весом до дерева, являющегося каркасом. При этом надстройку каждый раз следует выполнять ребром с наименьшим возможным весом, избегая появления циклов.
Исходим и ребра (3,5,0). Последовательное его расширение ребрами с наименьшим весом приводит нас к каркасу:
T={(3,5,0), (5,6,9), (4,5,7), (3,7,4), (3,9,2), (1,9,6), (2,9,1), (8,9,7)} c наименьшим весом 35.

Множество хорд H=E-T={(1,8,9),(2,5,2),(3,6,9), (4,9,9),(7,9,6)}
Последовательно возвращаем в каркас по одной хорде и получаем фундаментальную систему из шести циклов:
С1=1891, С2=25392, С3=3563, С4=45294, С5=7397
Всякий фундаментальный разрез составят хорды плюс одно произвольное ребро каркаса. Все фундаментальные разрезы:
H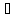 {(3,5,0)},
H
{(3,5,0)},
H {(5,6,9)},
H
{(5,6,9)},
H {(4,5,7)},
H
{(4,5,7)},
H {(3,7,4)},
H
{(3,7,4)},
H {(3,9,2)},
H
{(3,9,2)},
H {(1,9,6)},
H
{(1,9,6)},
H {(2,9,1)},
H
{(2,9,1)},
H {(8,9,7)}.
{(8,9,7)}.
Задача 7.21
В данном двудольном графе G = (V1 , V2 , E), V1 = { x1 , x2 , x3 , x4 , x5 },
V2 = { y1 , y2 , y3 , y4 , y5 , y6 }, найти совершенное сочетание паросочетаний. Если его нет, то указать получившееся максимальное паросочетание.
E = {(x1 , y6), (x1 , y4), (x1 , y1), (x2 , y5), (x2 , y6), (x3 , y4), (x3 , y2), (x3 , y6), (x4 , y3), (x4 , y2), (x4 , y5), (x5 , y2), (x5 , y1), (x5 , y5)}.
