2.2. Замена переменных в тройных интегралах

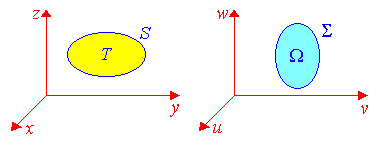Рис. 2.3

Рассмотрим вопрос о замене переменных в тройном интеграле. Содержание этого вопроса во многом аналогично вопросу о замене переменных в двойных интегралах. Рассмотрим два трехмерных пространства. Пусть в одном из них введены координаты x, y, z, а во втором – координаты u, v, w. Пусть, далее, T и  – две области в этих пространствах, ограниченные кусочно-гладкими поверхностями S и  соответственно (рис. 2.3). Предположим, что между точками этих областей установлено взаимно однозначное соответствие. Это соответствие может быть записано с помощью трех функций

x=x(u,v,w), y=y(u,v,w), z=z(u,v,w), (2.5)

или с помощью обратных функций

u=u(x,y,z), v=v(x,y,z), w=w(x,y,z). (2.6)

Предположим, что функции (2.5) и (2.6) не только непрерывны, но и имеют непрерывные частные производные первого порядка. Тогда якобианы

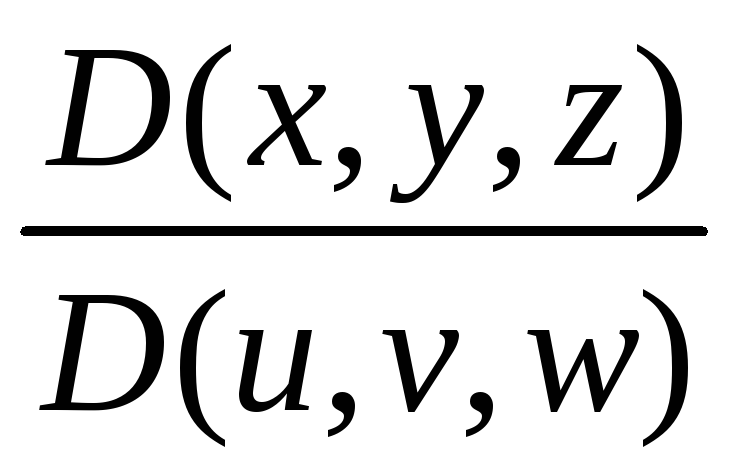и

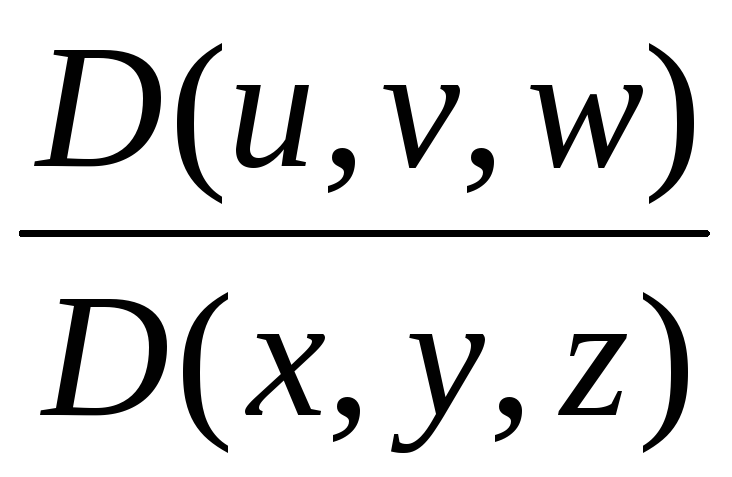
существуют и непрерывны. Мы будем предполагать, что каждый из этих якобианов отличен от нуля. В этом случае можно показать, что соответствие, определяемое формулами (2.5) и (2.6), переводит внутренние точки одной области во внутренние точки другой, а граничные точки – опять-таки в граничные.

Отображение (2.5) переводит область  в T. Следовательно, задание точки (u,v,w) из  вполне определяет соответствующую точку (x,y,z) из T. Иначе говоря, величины u,v,w можно рассматривать как координаты (отличные, конечно, от декартовых) точек области T. Они называются криволинейными координатами.

Рассмотрим в  плоскость, определенную условием u=u₀, т.е. параллельную координатной плоскости vw. Отображение (2.5) переводит ее в некоторую поверхность. Декартовы координаты точек этой поверхности суть

x=x(u₀,v,w), y=y(u₀,v,w), z=z(u₀,v,w). (2.7)

Придавая u₀ различные значения, мы получим некоторое семейство поверхностей, зависящее от u как от параметра. Плоскости v=v₀ и w=w₀ переходят при отображении (2.5) в два аналогичных семейства поверхностей в области T. Эти три семейства поверхностей называются координатными. Через каждую точку области T проходит по одной поверхности каждого из трех семейств.

Теорема. Рассмотрим взаимнооднозначное отображение замкнутой ограниченной области T в аналогичную область , заданную при помощи уравнение (2.5), непрерывное, непрерывно дифференцируемое и имеющее отличный от нуля Якобиан, и пусть f(x,y,z) – заданная в T непрерывная функция, тогда имеет место формула для замены переменных в тройном интеграле:

. (2.8)

Доказательство. Найдем теперь выражение для объема в криволинейных координатах. Рассмотрим три пары бесконечно близких между собой координатных плоскостей. Пусть из этих пар задается фиксированными з

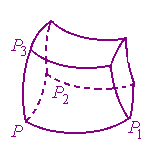Рис. 2.4

начениями первой координаты, равными соответственно u и u+du, вторая – значениями v и v+dv второй координаты и третья – значениями w и w+dw третьей координаты. Эти три пары поверхностей вырезают в пространстве бесконечно малый криволинейный параллелепипед. С точностью до бесконечно малых величин высшего порядка этот параллелепипед совпадает с прямоугольным параллелепипедом, ребрами которого служат векторы , и (рис.2.4). С точностью до бесконечно малых величин эти векторы имеют координаты

, ,

.

Как известно, объем параллелепипеда, построенного на трех векторах, равен абсолютной величине определителя, составленного из координат этих векторов. Следовательно,

,

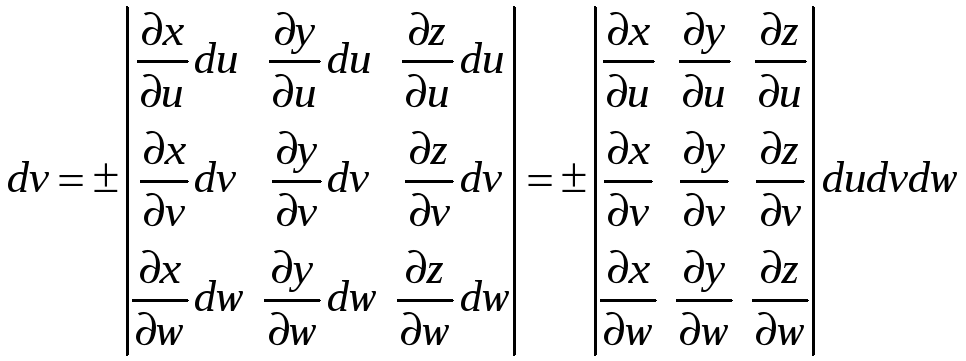где знак плюс или минус берется так, чтобы все выражение было положительно. Итак, мы получим, что

, (2.9)

где – якобиан преобразования (2.5).

Из формулы (2.9) следует, что объем конечной области T записывается в виде тройного интеграла

, (2.10)

взятого по той области  изменения переменных u,v,w, которая переводится в область T отображением (2.5).

Пусть f(x,y,z) – непрерывная функция, заданная в замкнутой ограниченной области T. При этих предположениях тройной интеграл

существует и он представляет собой предел интегральных сумм вида

.

В силу рассмотренных условий, каждому разбиению области T отвечает определенное разбиение области . Тогда

.

Применив к этому интегралу теорему о среднем, получим

,

где _i – объем частичной области _i, а – некоторая точка, принадлежащая _i. Пользуясь тем, что при составлении интегральной суммы точку (x_i,y_i,z_i) из области T_i можно выбирать произвольно, то возьмем

Тогда интегральная сумма примет вид

Полученная сумма является интегральной для правой части равенства (2.8). Что и требовалось доказать.