
2.3. Вычисление тройных интегралОв в цилиндрической системе координат
Рис.
2.5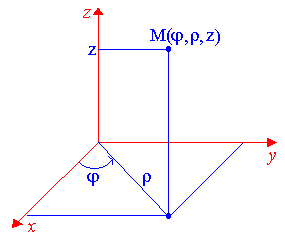
![]() ,
(2.11)
,
(2.11)
причем 02, 0+, –<z<+.
Модуль якобиана, соответствующий переходу от декартовых координат к цилиндрическим, равен
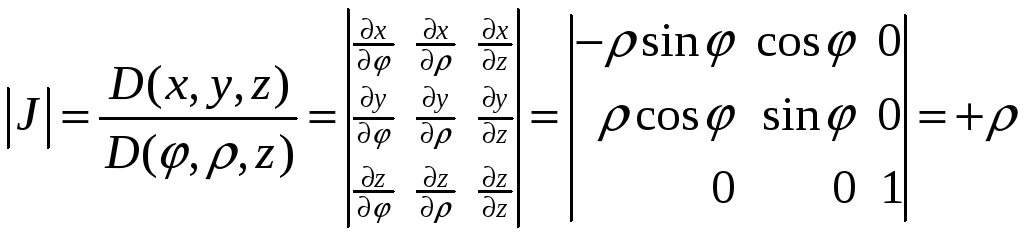 .
.
Таким образом, формула перехода для тройных интегралов от декартовых координат к цилиндрическим имеет вид
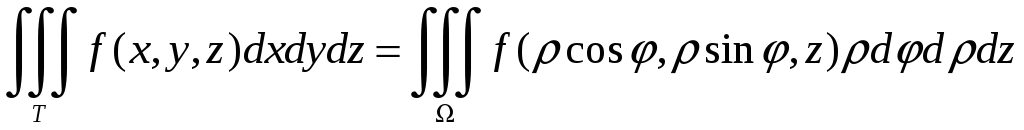 .
(2.12)
.
(2.12)
Вычисление тройных интегралов в цилиндрических координатах приводится к однократным повторным интегралам на основании тех же принципов, что и в случае декартовых координат. Обычно порядок интегрирования следующий: , , z. Тогда получаем
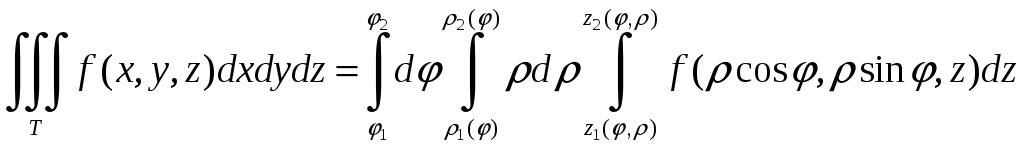 .
(2.13)
.
(2.13)
Пример 2.3. Вычислить интеграл
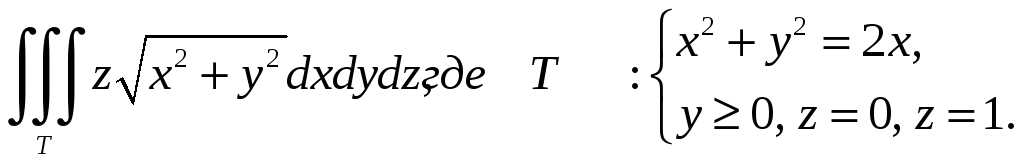
Р
Рис.
2.6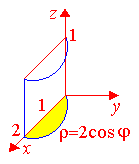
![]() .
.
На плоскости xOy это есть окружность радиуса 1 и с центром в точке C(1;0). В пространстве это есть цилиндр вдоль оси Oz, ограниченный плоскостями: y=0, z=0, z=1.
Перейдем в цилиндрическую систему координат (ЦСК). Уравнение цилиндрической поверхности в этих координатах примет вид
![]()
где
![]() В результате, получаем
В результате, получаем
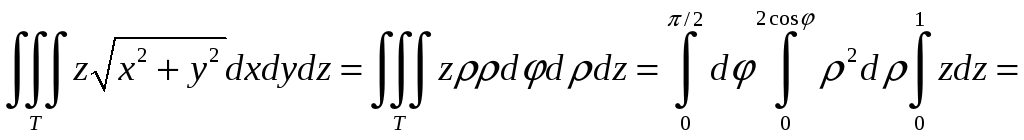
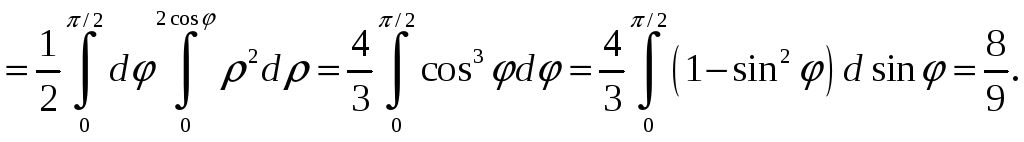
Пример 2.4. Вычислить объем тела, ограниченного поверхностями: y=0, x2+z2=y, x2+z2=9.
Р
Рис.
2.7
x = cos, z = sin, y = y.
Тогда
![]() .
.
При этом
![]()
В результате получаем, что объем искомой фигуры равен
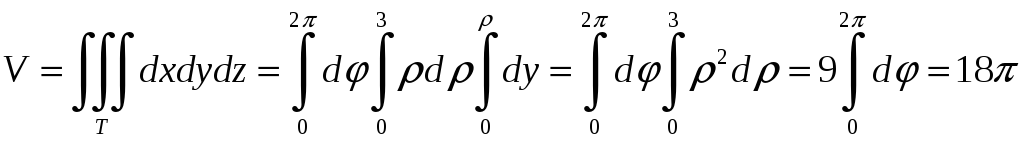 .
.
2.4. Вычисление тройных интегралОв в сферической системе координат
Е
Рис.
2.8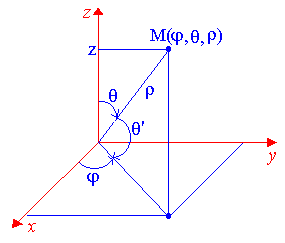
![]() (2.14)
(2.14)
причем 02, 0, 0<+.
Модуль якобиана, соответствующий переходу от декартовых координат к сферическим, равен
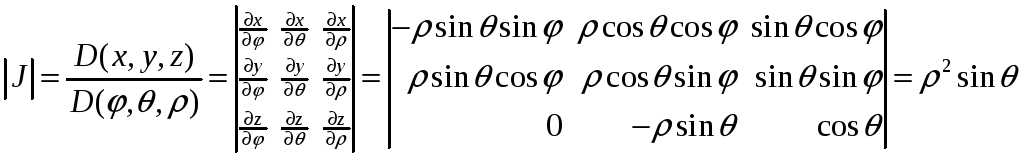 .
.
Таким образом, формула перехода для тройных интегралов от декартовых координат к сферическим имеет вид
 .
(2.15)
.
(2.15)
Вычисление тройных интегралов в сферических координатах приводится к однократным повторным интегралам на основании тех же принципов, что и в случае декартовых координат. Обычно порядок интегрирования следующий: , , . Тогда получаем
 .
(2.16)
.
(2.16)
Замечание. Отметим, что на практике иногда удобнее вместо угла использовать угол ', определяемый как угол между радиусом-вектором точки M и ее проекцией на плоскость xOy, т.е. между углами и ' существует взаимосвязь '=900-. Поэтому в некоторых учебниках за основу берется угол ', а не . В этом случае нужно sin заменить на cos', а cos – на sin', т.е.
![]() ,
(2.17)
,
(2.17)
причем
![]() .
.
П
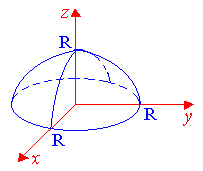 Рис.
2.9
Рис.
2.9
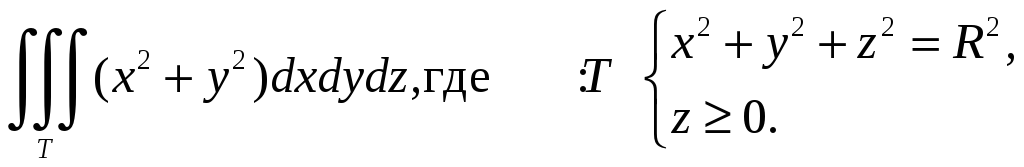
Решение. Сделаем чертеж. Перейдем в сферическую систему координат (ССК). Преобразует уравнения поверхностей.
![]()
![]()
Тогда
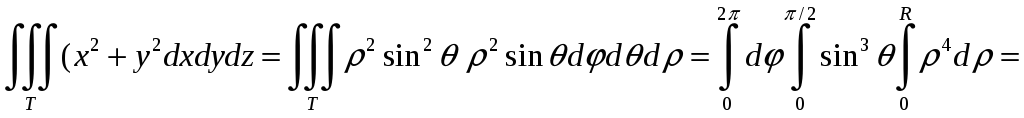
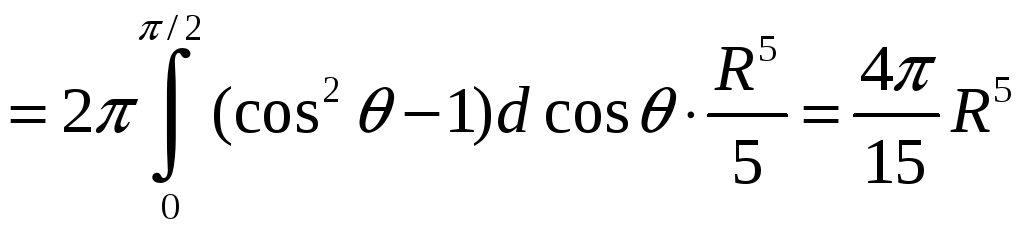 .
.
