1.8. Уравнения, допускающие понижение порядка

Рассмотрим некоторые типы дифференциальных уравнений n-го порядка, допускающие понижение порядка.

I. Уравнения вида .Общее решение получается путём n-кратного интегрирования

,

где .

Пример 12. Найти общее решение уравнения и его частное решение, удовлетворяющее начальным условиям.

Решение. Интегрируя первый раз, получаем:

.

Повторное интегрирование даёт:

.

–общее решение дифференциального уравнения.

Подставив теперь в полученное общее решение и выражение для первой производной начальные условия, получим систему двух уравнений с неизвестными :

Решив эту систему, найдём значения параметров . Следовательно, искомое частное решение имеет вид:

.

II. Уравнения вида , не содержащие явно искомой функции и её производных до порядкавключительно. С помощью заменыпорядок уравнения понижается наk единиц: .

Пример 13. Найти частное решение уравнения , удовлетворяющее начальным условиям.

Решение. Данное уравнение не содержит и. Положим, тогда, и уравнение принимает вид:

,

или

.

Это линейное уравнение первого порядка относительно функции . Решаем его методом Бернулли, т.е. делаем подстановку,:

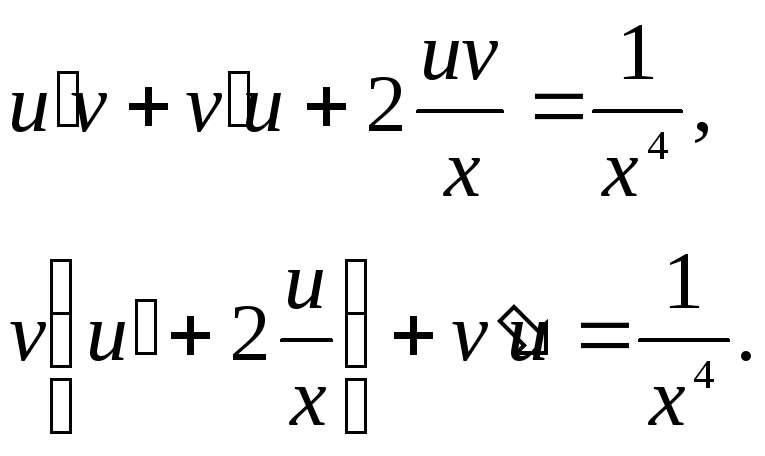
Выбираем функцию так, чтобы– это уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, получим:

.

Тогда

Учитывая, что , получаем:

Вспоминая, что , имеем:

.

Последовательно проинтегрировав 2 раза, найдём общее решение заданного дифференциального уравнения:

.

Используя начальное условие , получаем. Начальное условиепозволяет определить, а из условияследует, что. Итак, искомое частное решение есть.

III. Уравнения вида , не содержащие явно независимой переменной . Подстановкойи т.д. порядок уравнения понижается на единицу.

Пример 14. Найти общий интеграл уравнения .

Решение. Положим . Тогда уравнение преобразуется к виду:

.

Приведя подобные и сократив на (при этом следует учесть теряемое решение, или), получим:

.

Положив здесь , придём к уравнению

.

Сократив на z (при этом следует учесть ещё одно решение , т.е.), получим:

,

откуда

,

или

.

Интегрируя последнее уравнение, находим:

или

.

Окончательно получим: – общее решение исходного дифференциального уравнения. Заметим, что в общее решение входят найденные ранее частные решения.

IV. Уравнение вида , однородное относительно функции и её производных, т.е. такое, что . Подстановкой порядок уравнения понижается на единицу.

Пример 15. Найти общее решение уравнения .

Решение. Легко убедиться, что данное уравнение является однородным относительно функции у и её производных.

Положим . Тогдаи уравнение принимает вид:

.

Сокращая на (при этом получается решение), находим:

,

или

,

, откуда

.

Так как , то приходим к уравнению

,

или

, откуда

,

.

Это и есть общее решение, которое содержит и частное решение .

1.9. Линейные дифференциальные уравнения второго порядка

Определение. Линейным неоднородным дифференциальным уравнением второго порядка называется уравнение вида

, (16)

где функции инепрерывны на некотором отрезке

При этих условиях существует единственное решение уравнения (16), удовлетворяющее заданным начальным условиям: при.

Функция называетсяправой частью уравнения (16), а соответствующее уравнение называется также линейным дифференциальным уравнением второго порядка с правой частью. При приходим к линейному однородному дифференциальному уравнению второго порядка (или уравнению без правой части)

(17)

Определение. Функции иназываютсялинейно независимыми на отрезке , если тождество

(18)

имеет место тогда и только тогда, когда

Если же существуют такие числа и, из которых хотя бы одно отлично от нуля, что для всехимеет место тождество (18), то функциииназываютсялинейно зависимыми на отрезке .

Данные определения равносильны следующим:

функции иназываются линейно независимыми (зависимыми) на отрезке, если

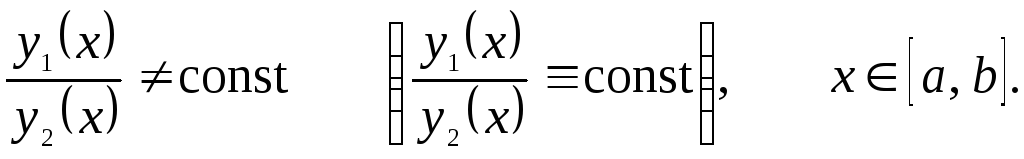
О линейной зависимости или независимости функций иможно судить по определителю

который называется определителем Вронского (или просто вронскианом).

Теорема 1. Если илинейно зависимы на отрезке, то определитель Вронскогодля всех.

Теорема 2. Если илинейно независимые на отрезкерешения дифференциального уравнения (17), то определитель Вронского этих функций отличен от нуля во всех точках отрезка, т.е.для всех.

Пример 16. Установить линейную зависимость или независимость данных пар функций на областях их определения:

а) ; б).

Решение. а) Функции иопределены на всей числовой прямой, т.е. приНаходим:,.

Вычислим определитель Вронского:

Следовательно, функции иявляются линейно независимыми.

б) Функции иопределены на всей числовой прямой, т.е. приНаходим:,.

Вычислим для них определитель Вронского:

для всех

Следовательно, функции иявляются линейно зависимыми.

Структура общего решения линейного дифференциального уравнения

Теорема 3. Общее решение линейного однородного дифференциального уравнения (17) имеет вид

,

где и– линейно независимые решения этого уравнения.

Таким образом, для того, чтобы получить общее решение однородного уравнения (17), достаточно найти любые два линейно независимых частных решения этого уравнения (в этом случае говорят, что они образуют фундаментальную систему решений уравнения (17)).

Теорема 4. Общее решение линейного неоднородного дифференциального уравнения (16) представляется в виде суммы

,

где – общее решение соответствующего однородного уравнения (17), а

–некоторое частное решение неоднородного уравнения (16).