
Федеральное агентство по образованию Российской Федерации
Филиал “СЕВМАШВТУЗ” государственного учреждения высшего профессионального образования “Санкт-Петербургский государственный морской технический университет”
в г. Северодвинске
Курзанова Е. В.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Конспект лекций. Часть 3
Северодвинск
2011
УДК 539.3/8
Сопротивление материалов. Конспект лекций. Часть 3 . /Сост.
Е.В. Курзанова, Северодвинск: РИО СЕВМАШВТУЗА, 2011 г. – 56 с.
Конспект лекций часть 3 предназначен для студентов всех специальностей, изучающих курс «Сопротивление материалов».
В части 3 конспекта лекций по сопротивлению материалов содержатся основные теоретические положения и зависимости по следующим темам: «Изгиб. Основные понятия и определения», «Закон Гука при изгибе», «Касательные напряжения при изгибе. Формула Журавского», «Сложное напряжённое состояние», «Продольный изгиб», «Гипотезы прочности», «Изгиб с растяжением», «Косой пространственный изгиб», «Внецентренное сжатие», «Совместное действие изгиба и кручения».
Рецензенты:
К.т.н., доцент кафедры №3 Н.В. Лобанов,
Генеральный директор ЗАО НТЦ «БАЗИС» В.А. Базанов.
Печатается по решению редакционно-издательского совета Севмашвтуза
© СЕВМАШВТУЗ, 2011г.
Содержание
Предисловие…………………………………………………………………….4
1. Лекция № 1 «Изгиб. Основные понятия и определения»………………5
2. Лекция № 2 «Закон Гука при изгибе. Условие прочности» »..……….12
3. Лекция № 3 «Касательные напряжения при изгибе. Формула Журавского» …………………………………………………………………...16
4. Лекция № 4 «Приближённое дифференциальное уравнение
упругой линии балки. Способы определения перемещений……………..19
5. Лекция № 5 «Сложное напряженное состояние.
Гипотезы прочности».......................................................................................31
6. Лекция № 6 «Продольный изгиб.
Формула Эйлера»……………………………………………………………...36
7. Лекция №7 «Изгиб с растяжением. Косой пространственный изгиб»……………………………………………………………………………43
8. Лекция № 8 «Внецентренное сжатие»……………………………………47
9. Лекция № 9 «Совместное действие изгиба и кручения»........................49
10. Вопросы для проверки уровня знаний.....................................................53
11. Список литературы………………………………………………………..55
Предисловие
В части 3 конспекта лекций содержаться основные теоретические положения и расчётные формулы по следующим темам: «Изгиб. Основные понятия и определения», «Закон Гука при изгтбе», «Касательные напряжения при изгибе. Формула Журавского», «Сложное напряжённое состояние. Гипотезы прочности», «Продольный изгиб», «Изгиб с растяжением», «Косой изгиб», «Внецентренное сжатие», «Совместное действие изгиба и кручения»
Целью конспекта лекций является оказание помощи студентам при изучении предмета, при решении и защите расчетно-графических работ по сопротивлению материалов.
Конспект лекций предназначен для студентов всех специальностей, изучающих курс “Сопротивление материалов”.
Лекция №1 «Изгиб. Основные понятия и определения»
Деформация изгиба рассматривается на примере тела, имеющего простую форму. Например, брус. Брусом называется твёрдое тело, у которого длина значительно больше поперечных величин одного порядка. Ось бруса может быть кривой или прямой линией. Брусья с прямолинейной осью называются стержнями, балками, стойками, в зависимости от назначения.
Брусья с прямолинейной осью, положенные на опоры и изгибаемые приложенными к ним нагрузками (равномерно распределённая нагрузка, сосредоточенная сила, изгибающий момент) называются балками.
Балки служат для передачи действующих на них нагрузок на опоры, на которых они покоятся. Если балка имеет свешивающиеся концы, такую балку принято называть консольной, свешивающиеся концы – консолями. На опорах балки возникают реакции, с определения которых следует начинать решение всех задач, связанных с изгибом балок.
В зависимости от числа и устройства опор балки число реакций, подлежащих определению, бывает различно. Опоры балок по их устройству могут быть разделены на следующие три основных типа:
-
Шарнирно-неподвижная опора. Такая опора не даёт концу балки возможности передвигаться в каком-либо направлении, позволяя ему только поворачиваться относительно центра шарнира О. Неизвестную по величине и направлению реакцию R всегда можно заменить двумя составляющими: вертикальной Rу по оси Oy и горизонтальной Rx по оси Ox.
-
Шарнирно-подвижная опора. Такая опора отличается от шарнирно неподвижной тем, что у неё опорная подушка поставлена на катки, дающие возможность передвигаться концу балки вдоль оси по опорной плоскости. Направление опорной реакции всегда перпендикулярно к оси балки.
-
Жёстко защемляющая опора. Такая опора препятствует всякому перемещению конца балки в плоскости действия внешних нагрузок. И ещё препятствует вращению конца балки. Неизвестную реакцию R можно всегда заменить двумя составляющими: вертикальной Rу по оси Oy и горизонтальной Rх по оси Ox. И ещё неизвестный реактивный момент МR, препятствующий повороту балки.
В практике при изгибе чаще всего силы действуют перпендикулярно к продольной оси балки. В этих случаях число неизвестных реакций, возникающих на опорах, уменьшается, так как реакция по оси Ox в шарнирно неподвижной опоре и жёстко защемляющей опоре становится равной 0.
Определение опорных реакций балок.
В случае действия на балку сил, лежащих в одной плоскости, статика даёт три уравнения равновесия:
![]()
 – сумма проекций
всех сил, приложенных к балке, вместе с
– сумма проекций
всех сил, приложенных к балке, вместе с
![]() реакциями опор на оси Ox
и Oy
равны 0.
реакциями опор на оси Ox
и Oy
равны 0.
![]() – сумма моментов
всех сил должная быть равна 0.
– сумма моментов
всех сил должная быть равна 0.
В случае действия
сил перпендикулярно оси Ox
уравнение
![]() обращается в тождество.
обращается в тождество.
Поперечная сила и изгибающий момент.
Для определения численного значения и направления поперечной силы и изгибающего момента применяют метод сечений. Для этого нужно мысленно разрезать балку сечением перпендикулярным к горизонтальной оси, отстоящем на расстоянии x от конца балки. Отбросив ту часть балки, где действует больше нагрузок, рассматривают равновесие оставшейся части. Все внешние силы, действующие на оставшуюся часть балки, могут быть заменены парой сил и силой, действующей в сечении.
Момент М
пары внутренних сил,
действующий в сечении, численно равный
алгебраической сумме моментов всех
внешних сил, действующих на оставшуюся
часть балки, называется
изгибающим моментом в сечении.
Всегда направлен в положительном
направлении, т. е. изгибает оставшуюся
часть балки выпуклостью вниз. Т. е. если
часть балки левая, то
![]() вращает оставшуюся часть балки против
часовой стрелки. Если часть балки правая,
то
вращает оставшуюся часть балки против
часовой стрелки. Если часть балки правая,
то
![]() вращает по часовой стрелке.
вращает по часовой стрелке.
Сила Q – результирующая внутренних сил, действующая в сечении, численно равная алгебраической сумме всех внешних сил, приложенных к оставшейся части балки, называется поперечной или перерезывающей силой в сечении. Поперечную силу будем считать положительной для левой части, если она действует вниз. Для правой части считается положительной действие поперечной силы вверх.
Изгиб бруса,
производимый двумя равными моментами,
направленными в противоположные стороны,
называется чистым
изгибом. В
поперечной сечении возникает только
один внутренний силовой фактор –
![]() .
.
Волокна, расположенные вдоль по длине балки, растягиваются по одной стороне; по другой – сжимаются. Вследствие удлинения одних волокон на выпуклой стороне и укорочения других на вогнутой стороне, вызываемых в брусе изгибающими моментами, в поперечных сечениях бруса возникают нормальные напряжения растяжения и сжатия (направлены перпендикулярно сечению). На границе между растянутым и сжатым слоем – нейтральный слой, волокна которого не растягиваются и не сжимаются, проходящий через центр тяжести сечения.
Поперечным
изгибом
называется изгиб бруса, при котором в
поперечном сечении возникает два
внутренних силовых фактора: Q
– поперечная или перерезывающая сила,
![]() – изгибающий момент. Поперечные силы
вызывают касательные напряжения.
– изгибающий момент. Поперечные силы
вызывают касательные напряжения.
При чистом и при поперечном изгибе плоские поперечные сечения остаются плоскими и после деформации. Плоские сечения взаимно поворачиваются одно относительно другого.
В случае чистого изгиба строят эпюру изгибающего момента.
В сечении, где
![]() имеет максимальное значение, вычисляют
нормальное напряжение. Это значение
напряжения сравнивают с допускаемым и
делают вывод: прочность обеспечена или
не обеспечена.
имеет максимальное значение, вычисляют
нормальное напряжение. Это значение
напряжения сравнивают с допускаемым и
делают вывод: прочность обеспечена или
не обеспечена.
В случае поперечного изгиба строят эпюру изгибающего момента и перерезывающей силы. По максимальному изгибающему моменту рассчитывают нормальное напряжение.
По максимальной перерезывающей силе рассчитывают касательное напряжение. С помощью нормального и касательного напряжения находят эквивалентное нормальное по гипотезе прочности. Эквивалентное значение напряжения сравнивают с допускаемым. Делают вывод об обеспечении прочности.
Для наглядности
изменения нагрузок по длине балки строят
эпюры поперечной силы
Q
и изгибающего момента
![]() .
.
Правила построения эпюр:
Балку разбивают на участки. Проводят вниз вертикальные линии в точках приложения сосредоточенных сил и сосредоточенных моментов. Нумерация участков слева направо, если балка на двух и более опорах. Если балка со свободным концом (жесткая заделка – консоль), нумерацию следует выполнять со свободной стороны.
-
Ниже проводят две базовые нулевые линии для построения эпюры поперечной силы Q и изгибающего момента
 .
. -
Положительные значения поперечной силы и изгибающего момента откладываются вверх от нулевой линии, отрицательные – вниз.
Для проверки
правильности нахождения опорных реакций
и определения внутренних силовых
факторов Q
и
![]() ,
исходя из условия равновесия для
оставшейся части балки, выполняют анализ
эпюр.
,
исходя из условия равновесия для
оставшейся части балки, выполняют анализ
эпюр.
Анализ правильности построения эпюр:
-
На участке, где нет равномерно-распределённой нагрузки, эпюра поперечной силы представляет собой прямую, параллельную нулевой оси. Эпюра изгибаюшего момента представляет собой наклонную прямую. В точке, где приложена сосредоточенная сила, на эпюре поперечной силы должен быть скачок, равный по величине сосредоточенной силе. На эпюре изгибающего момента изменяется угол наклона.
-
Если на участке есть равномерно-распределённая нагрузка, то эпюра поперечной силы представляет собой наклонную прямую. Эпюра изгибающего момента будет параболой. При действии равномерно-распределённой нагрузки вниз, значение поперечной силы на эпюре будет убывать. Эпюра изгибающего момента будет параболой выпуклостью вверх. В точке пересечении поперечной силой нулевой линии и смене знака с плюса на минус на эпюре изгибающего момента будет максимум. При действии равномерно-распределённой нагрузки вверх, значение поперечной силы на эпюре будет возрастать. Эпюра изгибающего момента будет параболой вогнутостью вниз. В точке пересечения нулевой линии и смене знака с минуса на плюс на эпюре изгибающего момента будет минимум.
-
В точке, где приложен сосредоточенный момент, на эпюре изгибающего момента должен быть скачок, равный по величине сосредоточенному моменту. На эпюре поперечной силы изменений нет.
-
При изгибе справедливы дифференциальные зависимости:
 - интенсивность равномерно-распределённой
нагрузки рана первой производной от
поперечной силы (тангенс угла наклона
эпюры поперечной силы)
- интенсивность равномерно-распределённой
нагрузки рана первой производной от
поперечной силы (тангенс угла наклона
эпюры поперечной силы)
 и второй производной от изгибающего
момента. Поперечная сила равна первой
производной от изгибающего момента и
равна тангенсу угла наклона касательной
к кривой изгибающего момента
и второй производной от изгибающего
момента. Поперечная сила равна первой
производной от изгибающего момента и
равна тангенсу угла наклона касательной
к кривой изгибающего момента

Примеры построения простейших эпюр.
Пример 1: Консоль нагружена сосредоточенным моментом, построить эпюры поперечной силы и изгибающего момента.
Эпюра поперечной силы представляет собой нулевую линию.
Эпюра изгибающего
момента представляет собой линию,
параллельную нулевой оси.
Решение: Проведем сечение на расстоянии
х
от
свободного, незакреплённого конца.
Поперечная или перерезывающей силы
![]() так как по условию равновесия отсечённой
части поперечная сила равна сумме
внешних сил, действующих на отсечённую
часть. Внешних сил, приложенных к
конструкции нет.
так как по условию равновесия отсечённой
части поперечная сила равна сумме
внешних сил, действующих на отсечённую
часть. Внешних сил, приложенных к
конструкции нет.
Положительное
направление изгибающего момента
![]() ,
принадлежащего сечению считается
направление по часовой. Изгибающий
момент должен нижние волокна растягивать
, верхние сжимать. В уравнении равновесия
для отсечённой части он будет взят со
знаком минус.
,
принадлежащего сечению считается
направление по часовой. Изгибающий
момент должен нижние волокна растягивать
, верхние сжимать. В уравнении равновесия
для отсечённой части он будет взят со
знаком минус.

От нулевой линии откладываем вниз.

Пример 2: Консоль
нагружена сосредоточенной силой,
построить эпюры поперечной силы и
изгибающего момента.Решение:
Проведем сечение на расстоянии х
от
свободного, незакреплённого конца.
Выберем положительное направление
поперечной перерезывающей силы
![]() и изгибающего момента
и изгибающего момента
![]() .
Положительным
считается направление поперечной силы
вверх. Так как она должна разворачивать
отсечённую часть по часовой
стрелке.
.
Положительным
считается направление поперечной силы
вверх. Так как она должна разворачивать
отсечённую часть по часовой
стрелке.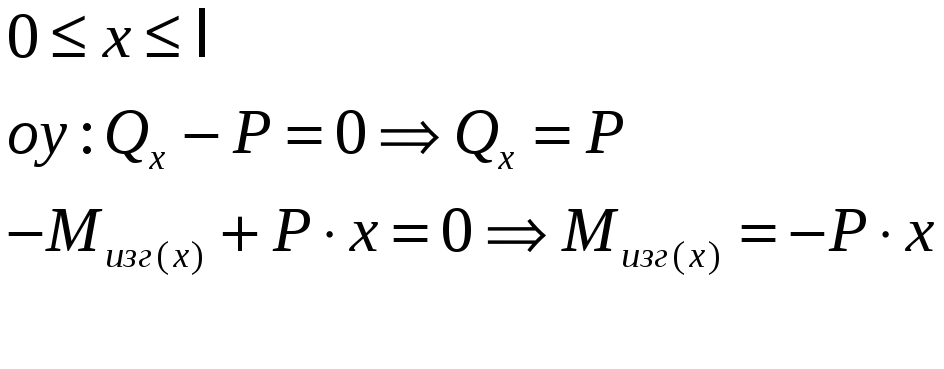 Вычисляем
значение изгибающего момента в граничных
точках участка при х=0
и
при х=l.
Вычисляем
значение изгибающего момента в граничных
точках участка при х=0
и
при х=l.
![]()
![]()
Строим эпюры поперечной силы и изгибающего момента.
Эпюра поперечной силы представляет собой линию, параллельную нулевой оси. Эпюра изгибающего момента представляет собой наклонную прямую.

![]()

Положительное направление поперечной силы - вверх. Положительное направление изгибающего момента – по часовой стрелке. Составляем уравнение равновесия для отсечённой части в проекциях на ось ОУ для действующих сил:
Границы участка
![]()

Составляем уравнение равновесия для моментов, действующих на отсечённую часть:

Вычисляем значение изгибающего момента в границах участка:

Пример 3: Балка, лежащая на двух опорах, нагружена сосредоточенной силой Р = 6Кн, построить эпюры поперечной силы и изгибающего момента.
Решение: Определяем опорные реакции в точках А и В.
 Хi=0
– сумма проекций всех действующих сил
на ось ОХ равна 0.
Хi=0
– сумма проекций всех действующих сил
на ось ОХ равна 0.
МА=0 – сумма моментов всех сил относительно точки А равна 0 .
МВ=0 – сумма моментов всех сил относительно точки В равна 0 .
Проверочное уравнение:Yi=0 – сумма проекций всех действующих сил на ось ОY равна 0.
 Хi=
Rвх
=0
Хi=
Rвх
=0
МА=-2Р+6 RВУ =0
МВ=4Р - 6 RАУ=0
RВУ=2 Кн
RАУ=4 Кн
Проверка: Yi= RВУ +RАУ – Р= 2 + 4 – 6=0
Составляем уравнения для поперечной силы и изгибающего момента для каждого участка:
I
участок
![]()

Выбираем положительное направление поперечной силы – вниз. Составляем уравнение равновесия в проекции на ось ОУ:

Выбираем положительное направление изгибающего момента – против часовой стрелки. Составляем уравнение равновесия для отсеченной части:

II
участок
![]()

Составляем уравнение равновесия в проекции на ось ОУ для второго участка, рассматривая все силы, действующие на отсечённую часть:


Вычисляем значение изгибающего момента в границах участка:


Проверка правильности построения эпюры. В точке, где приложена сосредоточенная сила, на эпюре поперечной силы должен быть скачок, равный сосредоточенной силе.
Лекция №2 «Нормальные напряжения при чистом изгибе. Закон Гука при изгибе. Условие прочности при изгибе».
Основной метод для определения внутренних силовых факторов в сопротивлении материалов – метод сечений. Он дает возможность определить поперечную силу и изгибающий момент. Каким образом распределяются напряжения по сечению балки при изгибе? Эту задачу можно решить, рассматривая деформации. При рассмотрении деформации растяжения-сжатия было установлено, что все волокна материала получают в направлении действия сил одинаковые относительные деформации. Следовательно, нормальные напряжения при растяжении-сжатии распределяются равномерно. Установим, каким образом распределяются напряжения по сечению при чистом изгибе с помощью деформаций.
Возьмём часть балки, изгибаемую двумя равными и противоположно направленными моментами.
M
N
– нейтральный слой. Нейтральный слой
не сжимается и не растягивается, он
искривляется. Кривизной нейтрального
слоя называется величина, обратная
радиусу кривизны
![]() ,
размерность
,
размерность
![]() ,
,![]() -
радиус кривизны.
-
радиус кривизны.

Точка О общий центр кривизны. Выделим элемент бруса между двумя сечениями (1 и 2).
Нейтральные волокна не изменили размера, а волокна на расстоянии у удлинились.
dS – длина нейтрального волокна
![]()
![]() -
абсолютное удлинение растянутого слоя.
-
абсолютное удлинение растянутого слоя.
Из подобия
треугольников
![]() и
и
![]() можно
записать следующее соотношение:
можно
записать следующее соотношение:

 -
отношение
абсолютного удлинения к первоначальной
длине равно относительной деформации
-
отношение
абсолютного удлинения к первоначальной
длине равно относительной деформации
![]() ,
следовательно
,
следовательно
![]() ,
,
это значит
![]() - относительная деформация прямо
пропорциональна расстоянию от нейтрального
слоя и обратно пропорциональна радиусу
кривизны.
- относительная деформация прямо
пропорциональна расстоянию от нейтрального
слоя и обратно пропорциональна радиусу
кривизны.
Так как волокна бруса при изгибе испытывают только простое растяжение или сжатие, то для определения распределения напряжений по сечению можно применить закон Гука при растяжении-сжатии.

По этой формуле можно выяснить, что распределение напряжений по сечению зависит от y .
При y=0
(нейтральный слой)
![]() 0
0
Максимальные напряжения будут в точке, для которой расстояние y наибольшее, т. е. на поверхности балки.
При отрицательном значении y меняется знак нормальных напряжений. Нормальные напряжения будут отрицательные.
Рассчитать
нормальные напряжения по формуле
невозможно, так как неизвестен радиус
кривизны
![]() .
Значит нужно перейти к известным
величинам, к изгибающему моменту
.
Значит нужно перейти к известным
величинам, к изгибающему моменту
![]() .
.
dМ – элементарный момент – момент, действующий на элементарную площадку. Равный произведению элементарной нормальной силы dN на плечо y.
 ,
,

Просуммируем
(проинтегрируем) все элементарные
моменты dМ
по всему сечению, получим
![]() ,
приложенный к сечению:
,
приложенный к сечению:

![]() -
изгибающий момент, берётся максимальное
значение с эпюры изгибающего момента.
-
изгибающий момент, берётся максимальное
значение с эпюры изгибающего момента.
Таким образом,
можно определить неизвестную величину![]()
 - закон Гука при
изгибе
- закон Гука при
изгибе
Кривизна нейтрального
слоя прямо пропорциональна изгибающему
моменту и обратно пропорциональна
произведению модуля Юнга на осевой
момент инерции сечения
![]() -
жёсткость сечения при изгибе.
-
жёсткость сечения при изгибе.
Вычислим значение напряжения в любой точке сечения

Нормальные напряжения в любой точке сечения прямо пропорциональны изгибающему моменту, расстоянию до нейтрального слоя и обратно пропорциональны осевому моменту инерции сечения.
Наибольшие нормальные напряжения на поверхности, при значении y=h/2

 - момент сопротивления
изгибу.
- момент сопротивления
изгибу.
 - момент сопротивления
изгибу для прямоугольного сечения,
геометрическая характеристика балки.
- момент сопротивления
изгибу для прямоугольного сечения,
геометрическая характеристика балки.
Условие прочности при изгибе:

Максимальные напряжения меньше или равны допускаемым. Прочность обеспечена.
При изгибе нейтральный слой проходит через центр тяжести сечения.
Для этого рассмотрим продольную силу, действующую в любом сечении, которая по условию равновесия равна сумме внешних сил, действующих на отсечённую часть балки.

Так как все силы упругости, действующие в сечении, равны внешним, при этом сумма всех внешних сил в проекциях на ось оx равна нулю (два внешних момента, созданные из системы двух равных и противоположно направленных сил, равны и противоположно направлены).
Значит
![]()
Заменим сумму на интеграл

Из всех слагаемых,
входящих в данную формулу только
статический момент площади сечения
![]() может равняться нулю, когда нейтральная
ось проходит через центр тяжести сечения.
может равняться нулю, когда нейтральная
ось проходит через центр тяжести сечения.
Это означает, что нейтральная ось проходит через центр тяжести сечения.
Лекция № 3 «Касательные напряжения при изгибе. Формула Журавского. Закон распределения касательных напряжений по сечению».
Рассмотрим балку, нагруженную внешней силой Р. Возникают нормальные и касательные напряжения. При этом касательные напряжения в силу закона парности направлены от ребра к ребру.

Выведем формулу для касательных напряжений. Для этого проведём через балку два вертикальных сечения на расстоянии dx друг от друга. И ещё горизонтальное сечение на расстоянии y от нейтрального слоя.
Таким образом, из балки выделили элемент с размерами: dx, h/2-y, b.
Для составления уравнений равновесия спроецируем все действующие силы на наш элемент на ось ох.

Получим, что
разность нормальных усилий
![]() уравновешивается действием касательного
усилия dT.
уравновешивается действием касательного
усилия dT.
![]()
Элементарное
касательное усилие dT,
возникающее на площадке
![]() будет
равно:
будет
равно:
![]()
Нормальные
напряжения, действующие на боковой
бесконечно малой площадке dF,
расположенной на уровне y
от нейтральной оси, будут рассчитываться
по известной формуле:

Усилие
![]() ,
приходящееся на элементарную площадку,
будет равно:
,
приходящееся на элементарную площадку,
будет равно:

На всю боковую
грань будет действовать сила
![]()

По аналогии на
следующую боковую грань, выделенного
элемента, действует сила
![]()


Выражая
![]() ,
получим:
,
получим:
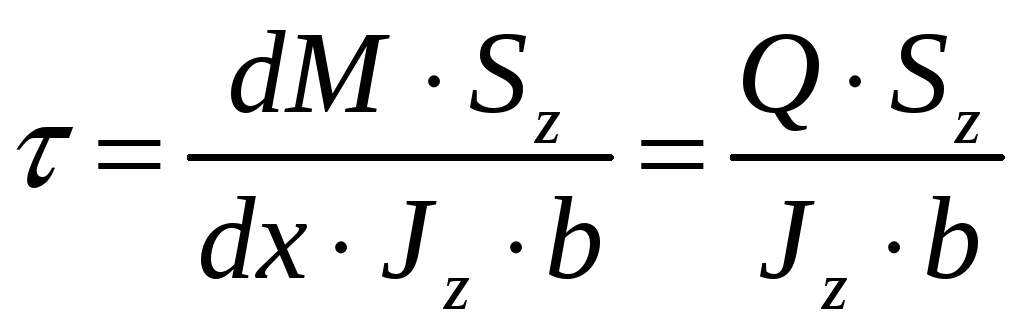 - формула Журавского
- формула Журавского
Касательные напряжения, лежащие выше нейтрального слоя, прямо пропорциональны поперечной силе, статическому моменту площади фигуры, обратно пропорциональны осевому моменту инерции сечения и ширине сечения.
Выясним с помощью формулы Журавского, каким образом касательные напряжения распределяются по сечению.


Подставим
![]() в формулу Журавского, учитывая что
осевой момент инерции для прямоугольного
сечения
в формулу Журавского, учитывая что
осевой момент инерции для прямоугольного
сечения
![]()

На нейтральной оси при y=0 касательные напряжения будут в полтора раза больше средних
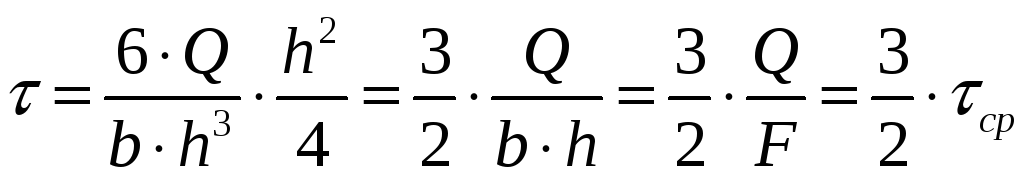
На нейтральном слое касательные напряжения принимают максимальное значение, нормальные напряжения на нейтральном слое равны нулю.
На поверхности балки касательных напряжений нет, только нормальные.
Наличие касательных напряжений несколько искажает принятую раньше схему деформации. Мы считали, что под действием изгибающих моментов поперечные сечения остаются плоскими и поворачиваются.
Под действием касательных напряжений элементы материала между двумя сечениями перекашиваются. Этот перекос в соответствии с изменением величины касательных напряжений возрастает от краев к нейтральной оси. Однако эти искривления мало отражаются на величине продольных деформациях волокон. Этот факт позволяет пользоваться формулой для нормальных напряжений

Лекция № 4 «Приближённое дифференциальное уравнение упругой линии балки. Способы определения перемещений».

Нужно получить зависимость y – деформации от x – длины.
При получении зависимости пренебрегаем влиянием поперечной силы,
т. е. рассматриваем случай чистого изгиба.
Уже известен закон Гука при изгибе:
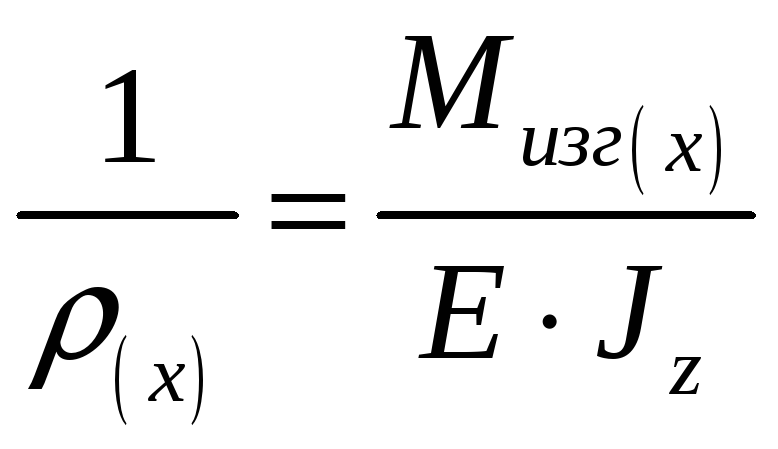 ,
,

Влияние поперечной
силы
![]() на
деформации невелико, поэтому ею
пренебрегаем.
на
деформации невелико, поэтому ею
пренебрегаем.
С другой стороны существует математическая зависимость между радиусом кривизны оси и координатами её точек х и y :
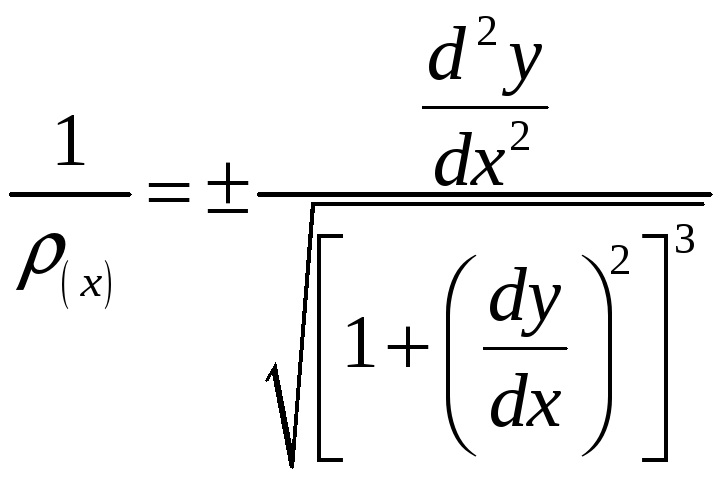
Слагаемое
![]() Очень малая величина, квадратом которой
можно пренебречь. Тогда приравнивая
правые части уравнений, получим:
Очень малая величина, квадратом которой
можно пренебречь. Тогда приравнивая
правые части уравнений, получим:

Это уравнение называется приближённым дифференциальным уравнением изогнутой оси балки.
Следует ставить знак « - » при направлении оси оy вниз,
И знак « + » при направлении оси вверх.
Условимся в дальнейшем всегда ось оy направлять вверх и дифференциальное уравнение можно переписать в следующем виде:

Определение перемещений при поперечном изгибе интегрированием дифференциального уравнения изогнутой линии балки.
Интегрируя первый раз, получим:
![]()
Разделив на
жёсткость сечения
![]() ,
получим уравнение для углов поворота
сечений:
,
получим уравнение для углов поворота
сечений:
 ,
,
где С первая постоянная интегрирования. Определяем из граничных условий:
Для балки с одной точкой опоры (консоль) угол поворота в точке опоры равен нулю:
![]()
Для балки на двух и более опорах углы поворота в опорах будут принимать максимальные значения. Угол поворота будет равен нулю на границе между участками. Если на эпюре изгибающего момента есть вершина параболы, то можно взять значение х в том месте, где на эпюре изгибающего момента максимум:
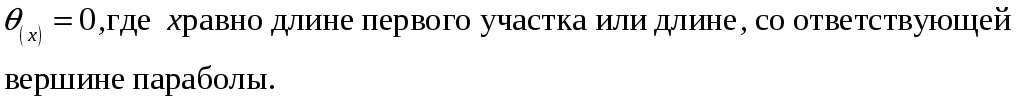
Интегрируя уравнение для углов поворота ещё раз, получим уравнение перемещений (прогибов):
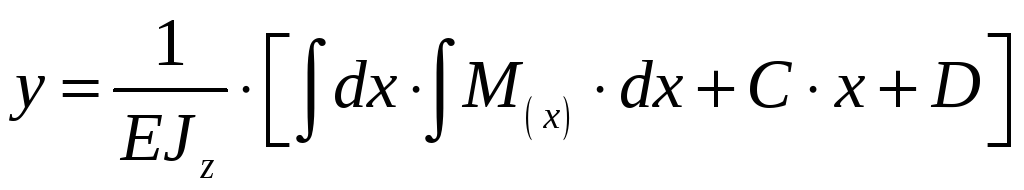 ,
,
где D вторая постоянная интегрирования. Определяем из граничных условий:
Для балки с одной точкой опоры перемещение в точке опоры равно нулю:
![]()
При найденном уже значении С, можно вычислить D. Для балки с одной точкой опоры максимальное перемещение будет на свободном конце (при х=0) и будет равно:
 ,
,
где
![]() - жесткость сечения при изгибе. Если
знак « + », перемещение направлено вверх
и совпадает с направлением вверх оси
оу.
Если знак « - », то перемещение направлено
вниз.
- жесткость сечения при изгибе. Если
знак « + », перемещение направлено вверх
и совпадает с направлением вверх оси
оу.
Если знак « - », то перемещение направлено
вниз.
Мы научились находить перемещение, если участок один.
Граничные условия выбираются в зависимости от конструкции балки.
Для балки с защемлённым концом (консоль) граничные условия будут следующие:
Перемещения и угол поворота сечения будут равны нулю в точке защемления при значении расстояния х, равном длине консоли.
Для балки на двух опорах значения перемещений в точках опоры, при значениях расстояний х, соответствующих точкам опоры, равняются нулю.
Таким способом вычисляют значение перемещения, если количество участков в конструкции не больше двух. Недостаток в том, что интегрирование каждого участка даёт две постоянные интегрирования.
Если участков два, то неизвестных постоянных интегрирования будет четыре.
К двум граничным условиям (равенства нулю перемещений или углов поворота в определённых точках и при определённом значении длины), указанным выше, нужно добавить ещё два условия: плавности и непрерывности изогнутой линии балки на границе между участками.
Условие плавности – углы поворота сечений на границе участков равны:
![]() ;
;
Условие непрерывности изогнутой линии – перемещения на границе участков одинаковы:
![]()
Решить систему из четырёх уравнений, где будет четыре неизвестные постоянные интегрирования, можно определить максимальное значение перемещения.
Пример 1. Определить максимальное перемещение консольной балки, длинной l, если к свободному концу приложена нагрузка Р.
Решение: Запишем приближённое дифференциальное уравнение изогнутой линии:
 ,
,
Проинтегрируем первый раз, получим:
 ,
,
Определим значение постоянной интегрирования С из граничных условий – угол поворота в точке опоры при х=l будет равен нулю:
 .
.
Интегрируем второй раз для определения перемещения:
 ,
,
Определим значение D из граничных условий – перемещение в точке опоры, при х = l, будет равно нулю:
 ,
,
После нахождения постоянных интегрирования, определим максимальное перемещение, которое будет на краю балки, при х=0:
 .
.
Определение перемещений методом начальных параметров.
Метод начальных параметров является более удобным для балок с большим количеством участков. Суть метода начальных параметров заключается в выравнивании констант интегрирования по участкам. В результате неизвестными остаются лишь две из них:
![]()
Оставшиеся константы интегрирования имеют простой физический смысл:

Для произвольной
балки постоянного по длине сечения,
нагруженной k
моментами
![]() и m
сосредоточенными силами
и m
сосредоточенными силами
![]() ,
включая
реакции опор, а также n
равномерно-распределёнными
нагрузками
,
включая
реакции опор, а также n
равномерно-распределёнными
нагрузками
![]() уравнения
углов поворота и прогибов записываются
одним уравнением сразу для всей балки
(для всех участков)
уравнения
углов поворота и прогибов записываются
одним уравнением сразу для всей балки
(для всех участков)
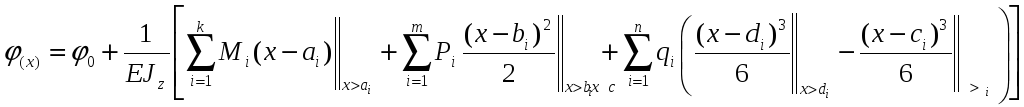

где
![]() -
координата
сечения, где приложена i
сосредоточенный момент
-
координата
сечения, где приложена i
сосредоточенный момент
![]() ;
;
![]() - координата
сечения, где приложена i
сосредоточенная сила
- координата
сечения, где приложена i
сосредоточенная сила
![]() ;
;
![]() - координаты начала
и конца i
равномерно - распределённой нагрузки.
- координаты начала
и конца i
равномерно - распределённой нагрузки.
Двойные чёрточки у каждого из слагаемых показывают, при каком условии данное слагаемое включается в вычисления, а именно при определении прогибов и углов поворота в произвольном сечении с координатой – х. В выше приведённых уравнениях удерживаются только те слагаемые, которые учитывают нагрузки, приложенные к балке левее рассматриваемого сечения.
В уравнениях
метода начальных параметров принято
следующее правило знаков для внешних
нагрузок:
![]() ,
если он
направлен по
часовой
стрелке;
,
если он
направлен по
часовой
стрелке;
![]() > 0 и
> 0 и
![]() >
0, если они направлены вверх.
>
0, если они направлены вверх.
Пример 2. Определить углы поворота сечений в точках А и В, максимальное перемещение балки, расположенной на двух опорах методом начальных параметров. Длина балки l = а + в. На границе участков приложена нагрузка Р.

Для определения опорных реакций составляем уравнения равновесия:

Хi= Rвх = 0
![]()
![]()

Проверка: Уi= RАУ + RBУ – Р = 0
Для решения применяем метод начальных параметров.
Определяем с помощью граничных условий следующие неизвестные:

Для балки, расположенной на двух опорах, перемещения в точках А и В равны нулю, поэтому два граничных условия имеют следующий вид:
Перемещения в точках А и В равны нулю.

Для определения прогиба начального сечения и угла поворота начального сечения воспользуемся уравнением перемещений и граничными условиями.
Уравнение перемещений для любого сечения:
 Используя
начальные условия:
Используя
начальные условия:
![]()
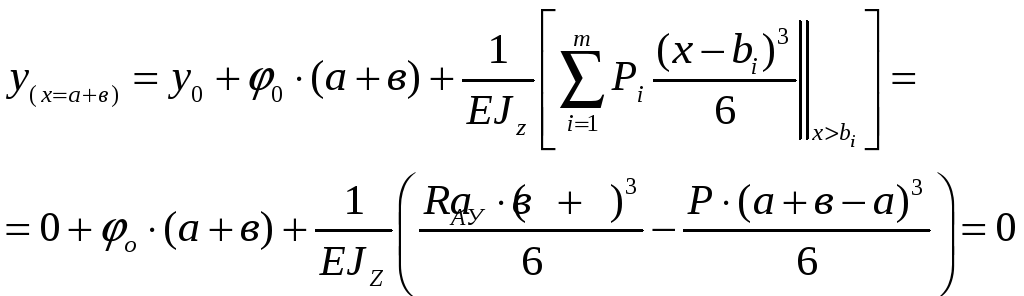
Определяем
![]() из выше указанного уравнения:
из выше указанного уравнения:

Подставим в
уравнение найденное ранее значение
![]() ,
,
учитывая, что l = а + в, после упрощений, получим:
Начальный угол поворота или угол поворота сечения в точке А равен:
![]()
Знак « - » означает поворот угла по часовой стрелке.
Определим перемещение
в точке С -
![]()
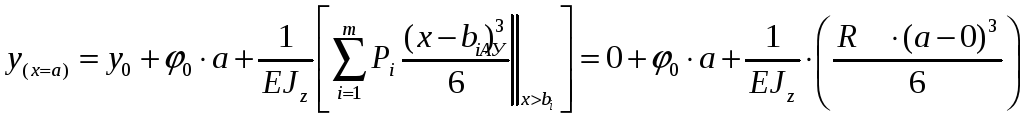
Подставим в
уравнение значение
![]() и
и
![]() получим:
получим:

Перемещение в точке С:

Знак « - » означает перемещение вниз.
Определим угол поворота конечного сечения
![]()
Для этого воспользуемся формулой для угла поворота метода начальных параметров:


После подстановки
значения
![]() и упрощений,
получим:
и упрощений,
получим:

Угол поворота сечения точки В равен:
![]()
Знак « + » означает поворот угла против часовой стрелки.
Определение перемещений энергетическими методами.
Рассмотренные выше методы неприменимы для балок с криволинейной осью и для рам. Более универсальными в этом смысле являются энергетические методы. Наиболее популярным является метод Мора (интеграл Мора).
Согласно методу Мора рассматриваются два состояния системы (балки, рамы): грузовое и единичное.
Грузовое состояние обусловлено действием на систему заданной внешней нагрузки. Возникающие при этом силовые факторы и их эпюры называются грузовыми.
Единичное состояние обусловлено действием на систему единичной обобщённой нагрузки, приложенной по направлению искомого перемещения. Возникающие при этом силовые факторы и их эпюры называются единичными. Под обобщённой нагрузкой понимается либо сосредоточенная сила, либо сосредоточенный момент. Обобщённой нагрузке соответствуют обобщённые перемещения. Сосредоточенной силе соответствует линейное перемещение. Сосредоточенному моменту соответствует угол поворота сечения.
Пренебрегая перемещениями, связанными с деформацией сдвига ввиду их малости по сравнению с деформацией изгиба интеграл Мора для случая прямого плоского изгиба запишется в виде:

Во всех энергетических методах знак результата означает:
Знак « + » - искомое перемещение совпадает по направлению с приложенной единичной нагрузкой.
Знак «-» - искомое перемещение противоположно по направлению приложенной единичной нагрузке.
Графический способ вычисления интеграла Мора – способ Верещагина.
Формула Верещагина записывается в виде:

Знак « + » - когда площадь грузовой эпюры совпадает по направлению с эпюрой от единичной нагрузки.
Знак «-» - когда площадь грузовой эпюры противоположна по направлению эпюре от единичной нагрузки.
Минимальное количество слагаемых в формуле Верещагина равно количеству участков эпюры единичного момента. Если границы эпюры грузового момента не совпадают с границами эпюры единичного момента, то грузовую эпюру необходимо дополнительно разбить по границе единичной эпюры.
Если имеются трудности с определением площадей и положений центров тяжести участков грузовых эпюр, то для вычисления интеграла Мора
Рационально использовать формулу Симпсона-Корнаухова:

Формула Симпсона - Корнаухова справедлива для конструкций с прямыми участками (для балок и рам). Грузовая эпюра должна быть линейна или является параболой не выше второй степени.
Отметим, что перемещения, определённые с помощью дифференциального уравнения изогнутой линии балки и с помощью энергетического метода получаются одинаковыми по абсолютной величине.
Для оценки величины
полученной деформации вычисляют значение
перемещения
![]() балки. Значения
балки. Значения
![]() приведены в учебниках по сопротивлению
материалов для различных случаев
нагружения балок.
приведены в учебниках по сопротивлению
материалов для различных случаев
нагружения балок.
Величина прогиба
нужна для проверки условия жёсткости:
максимальный прогиб не должен превышать
допускаемого. Можно воспользоваться
значением
![]() из справочника при вычислении значения
приложенных нагрузок.
из справочника при вычислении значения
приложенных нагрузок.
Пример: Вычислим значение реакции средней опоры для двухпролётной неразрезной балки с консолями, где
l – длина пролёта;
![]() – длина консоли;
– длина консоли;
Р – нагрузка.
Для вычисления
величины прогиба
![]() от сил Р
воспользуемся методом Верещагина. Для
этого нужно площадь грузовой опоры
умножить на значение реакции средней
опоры для двухпролётной неразрезной
балки с консолями.
Для
вычисления величины прогиба
от сил Р
воспользуемся методом Верещагина. Для
этого нужно площадь грузовой опоры
умножить на значение реакции средней
опоры для двухпролётной неразрезной
балки с консолями.
Для
вычисления величины прогиба
![]() от сил Р
воспользуемся методом Верещагина. Для
этого нужно площадь грузовой опоры
умножить на значение реакции средней
опоры для двухпролётной неразрезной
балки с консолями.
от сил Р
воспользуемся методом Верещагина. Для
этого нужно площадь грузовой опоры
умножить на значение реакции средней
опоры для двухпролётной неразрезной
балки с консолями.
Для вычисления
величины прогиба
![]() от сил Р
воспользуемся методом Верещагина:
от сил Р
воспользуемся методом Верещагина:

Для этого нужно площадь грузовой эпюры умножить на ординату эпюры от единичной нагрузки, находящуюся на одной линии с центром тяжести площади грузовой эпюры, получаем:
 ,
,
где
![]() – жёсткость сечения.
– жёсткость сечения.
Значение величины
прогиба
![]() ,
возникающее от действия силы
,
возникающее от действия силы
![]() ,
приложенной в середине, возьмём из
справочника по сопротивлению материалов:
,
приложенной в середине, возьмём из
справочника по сопротивлению материалов:
![]() .
.
Приравнивая
величины прогибов
![]() ,
,
получим:
 ,
следовательно:
,
следовательно:
![]()

Лекция № 5 « Сложное напряжённое состояние. Гипотезы прочности»
Сложным называется напряжённое состояние при котором на трех взаимно-перпендикулярных площадках действуют нормальные и касательные напряжения.
Напряжение, перпендикулярное площадке называется нормальным и вычисляется по формуле:

Напряжение, расположенное на площадке, называется касательным и вычисляется по формуле:

Оказывается при любом сложном напряжённом состоянии тела через каждую его точку можно провести три взаимно-перпендикулярные площадки, где будут отсутствовать касательные напряжения. Только нормальные.
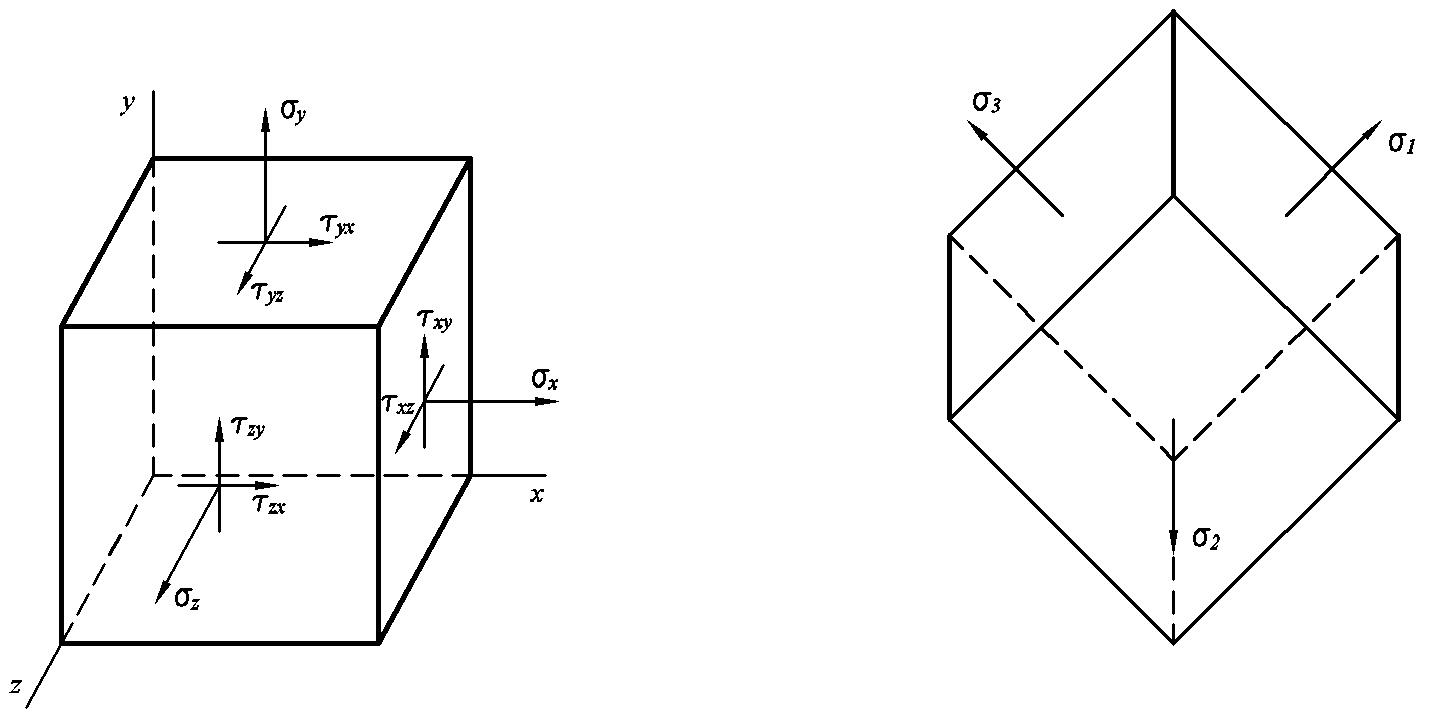
При этом они
распределяются следующим образом
![]() .
.
Например: 200 МПа > 150 МПа > 120 МПа.
![]() ;
;
![]() ;
;
![]() ,
,
С учётом знака:
![]() ;
;
![]() ;
;
![]()
Площадки, на которых действует только один вид напряжений, называются главными.
В зависимости от количества главных напряжений, приложенных к главным площадкам, различают три вида напряжённого состояния в точке:
-
Все 3 главных напряжения не равны нулю. Такое напряжённое состояние называется объёмным (например, подводная лодка под водой).
-
Если одно из главных напряжений равно нулю. Такое напряжённое состояние называется плоским. Например, вал. В этом случае он испытывает сжатие по двум направлениям, при условии, если шкив не вращается. При вращении шкива появится ещё касательное напряжение, действующее на вал.
-
Одно главное напряжение не равно нулю. Такое напряжённое состояние называется линейным. Простое растяжение или сжатие.
В случае сложного напряжённого состояния необходимо привести все действующие напряжения к линейному состоянию и рассматривать сложное напряжённое состояние как простое линейное растяжение или сжатие.
Сначала определим главные напряжения для плоского напряжённого состояния, избавившись от касательных напряжения:
Для этого вырежем
у детали элемент. Напряжения
![]() не будут главными, так как действуют
ещё и касательные напряжения.
не будут главными, так как действуют
ещё и касательные напряжения.
Существуют формулы, позволяющие переходить от не главных напряжений к главным напряжениям:
![]()
Получили плоское напряжённое состояние.
Для проверки
прочности достаточно сравнить наибольшее
главное
![]() или модуль главного напряжения
или модуль главного напряжения
![]() (при отрицательном значении) с допускаемым
(при отрицательном значении) с допускаемым
![]() .
.
Если
![]() ,
значит прочность будет
обеспечена
,
значит прочность будет
обеспечена

Для хрупких материалов максимальные отрицательные значения сравнивают с допускаемым значением на сжатие, положительные на растяжение. При этом коэффициент запаса прочности п=2.
Рассмотрим вторую обратную задачу:
При известных главных напряжениях нужно найти нормальные и касательные напряжения в любой точке наклонного сечения.
Дано:
![]() ,
напряжения действуют по двум взаимно
перпендикулярным направлениям - плоское
двухосное напряжённое состояние.
,
напряжения действуют по двум взаимно
перпендикулярным направлениям - плоское
двухосное напряжённое состояние.
Найти:
![]() ,
нормальное и касательное напряжения,
действующие в наклонном сечении.
,
нормальное и касательное напряжения,
действующие в наклонном сечении.

Рассмотрим отдельно
действие
![]()
Напряжения в
наклонных сечениях от действующего
напряжения
![]() будут равны:
будут равны:

Рассмотрим действие
напряжения
![]() ,
действующее к наклонному сечению под
углом
,
действующее к наклонному сечению под
углом
![]()
Напряжения в
наклонных сечения от действующего
напряжения
![]() будут равны:
будут равны:

Если сложить все нормальные и касательные напряжения в наклонном сечении, получим полные нормальные и касательные:

Если в формулу для
![]() подставить значение
подставить значение
![]() ,
то при любом значении угла
,
то при любом значении угла
![]() ,
напряжение в наклонном сечении -
,
напряжение в наклонном сечении -![]() всегда будет меньше
всегда будет меньше
![]() ,
так как
,
так как
![]() всегда
меньше единицы, а в число меньшее единицы
в квадрате будет ещё меньше.
всегда
меньше единицы, а в число меньшее единицы
в квадрате будет ещё меньше.
Это значит, что из всех напряжений главные самые большие.
Рассмотрим случай
действия всех главных напряжений
![]() .
Объёмное напряженное состояние. Если
в направлении действия
.
Объёмное напряженное состояние. Если
в направлении действия
![]() будет происходить растяжение, то в
направлении
будет происходить растяжение, то в
направлении
![]() будет происходить сжатие. Можно привести
к обобщённому закону Гука.
будет происходить сжатие. Можно привести
к обобщённому закону Гука.
![]()
или
![]() ,
если
,
если
![]()
![]() уменьшают действие
уменьшают действие
![]() .
.
Аналогично для
относительных деформаций
![]() можно записать:
можно записать:
![]()
![]()
Из всех относительных
деформаций
![]() будет самая большая.
будет самая большая.
Если
![]() будут действовать внутрь, то будет знак
« + ».
будут действовать внутрь, то будет знак
« + ».
Гипотезы прочности.
Гипотезы прочности – предположения о причинах разрушения материала или теории прочности.
I
теория прочности – гипотеза
наибольших нормальных напряжений. Была
сформулирована Галилеем в 1628г. В основу
теории наибольших нормальных напряжений
положена гипотеза о преимущественном
влиянии наибольших по абсолютной
величине нормальных напряжений.
Разрушение наступает тогда, когда
наибольшее из главных напряжений -
![]() достигает величины опасной для данного
материала. Условие прочности в этом
случае имеет следующий вид:
достигает величины опасной для данного
материала. Условие прочности в этом
случае имеет следующий вид:
![]()
Считается очень
приблизительной, не учитывает действие
других главных напряжений
![]() .
Данная гипотеза удовлетворяет результатам
испытаний деталей из хрупких материалов:
чугун, камень, кирпич.
.
Данная гипотеза удовлетворяет результатам
испытаний деталей из хрупких материалов:
чугун, камень, кирпич.
II теория прочности – гипотеза наибольших относительных удлинений. Была предложена Мариоттом в 1628г. Согласно этой теории опасное состояние материала наступает тогда, когда наибольшее из относительных удлинений достигает опасной величины. В основе лежит обобщенный закон Гука.
![]()
Или для напряжений:
![]()
В настоящее время
данная теория при расчётах не используется.
Ряд недостатков: получается, что
эквивалентное напряжение
![]() ,
как более опасное, чем главное напряжение
,
как более опасное, чем главное напряжение
![]() ,
сравнивается с допускаемым
,
сравнивается с допускаемым
![]() .
На самом деле главное напряжение
.
На самом деле главное напряжение
![]() - наибольшее. Также как и в предыдущей
теории не учитывается действие касательных
напряжений
- наибольшее. Также как и в предыдущей
теории не учитывается действие касательных
напряжений
![]() .
.
III теория прочности – гипотеза действия наибольших касательных напряжений. Была предложена Кулоном а 1773г. Касательные напряжения достигают величины, при которой начинается текучесть материала.
![]() - см. ранее полученную
формулу.
- см. ранее полученную
формулу.
При
![]() ,
,
С учётом действия касательных напряжений (см. ранее приведённые формулы перехода к главным напряжениям):
![]()
Практически подтверждается для пластичных материалов, для хрупких нет.
Для оценки сложного напряжённого состояния для хрупких материалов выше указанная формула была дополнена Мором (V теория прочности) и переписана в следующем виде:
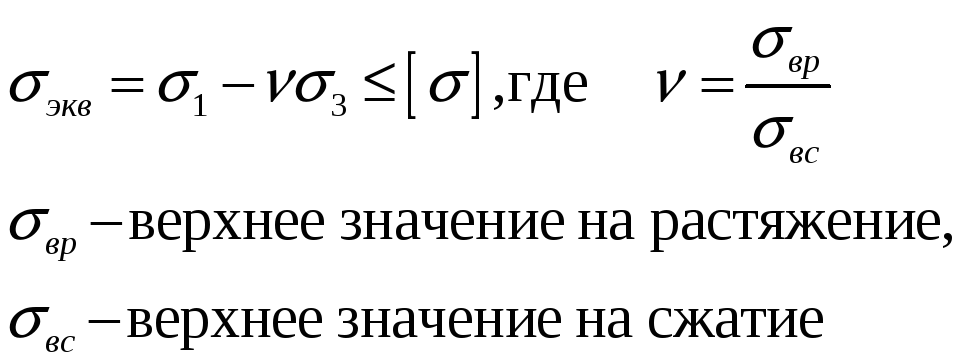
Теория прочности Мора позволяет учесть различие в свойствах материалов при растяжении и при сжатии присущее малопластичным и хрупким материалам.
IV теория прочности – гипотеза наибольшей потенциальной энергии формоизменения. Была предложена Бельтрами в 1885г. и Губером в 1904г.;

Если в данную
формулу подставить главные напряжения
![]() в указанном ниже виде, приравнивая к
нулю
в указанном ниже виде, приравнивая к
нулю
![]()
![]()
Формулу для эквивалентного напряжения можно упростить:
![]()
В настоящее время из пяти гипотез прочности используются лишь последние три, в зависимости от материала и вида нагружения. Расчёты на прочность по гипотезам прочности во многих случаях избавляют проектировщиков и конструкторов от необходимости подвергать проектируемые конструкции и детали непосредственным испытаниям на прочность.
Лекция №6 «Продольный изгиб. Формула Эйлера. Условие устойчивости сжатых стержней».

Нужно найти формулу
зависимости
![]() - критической силы (минимальное значение
сжимающей силы, при которой возможен
продольный изгиб) от геометрических
размеров стержня и механических
характеристик материала. Данная формула
была выведена знаменитым математиком
и механиком Леонардом Эйлером в 1744г.
- критической силы (минимальное значение
сжимающей силы, при которой возможен
продольный изгиб) от геометрических
размеров стержня и механических
характеристик материала. Данная формула
была выведена знаменитым математиком
и механиком Леонардом Эйлером в 1744г.
Определим изгибающий
момент
![]() методом сечений. Запишем условие
равновесия для оставшейся части:
методом сечений. Запишем условие
равновесия для оставшейся части:
![]() - изгибающий момент
в любом сечении стержня.
- изгибающий момент
в любом сечении стержня.
у – уравнение упругой линии стержня
 - синусоида, знак
«-», так как расположена ниже нулевой
оси;
- синусоида, знак
«-», так как расположена ниже нулевой
оси;
f – величина стрелы прогиба.
На концах стержня при х=0 и при х=l у=0 прогиба не будет.
Посередине стержня
при


Подставим значение
![]() в приближённое дифференциальное
уравнение упругой линии:
в приближённое дифференциальное
уравнение упругой линии:

Проинтегрируем один раз, получим:

Найдём постоянную
интегрирования из граничных условий
при
![]()
 , так как касательная
к упругой линии в середине стержня
параллельна оси ох.
Следовательно С
= 0.
, так как касательная
к упругой линии в середине стержня
параллельна оси ох.
Следовательно С
= 0.
Проинтегрируем во второй раз, получим:

Найдём постоянную интегрирования D из условия: при при х=0 прогиб у=0, следовательно D=0.
Значит:

Так как при
 ,
следовательно:
,
следовательно:
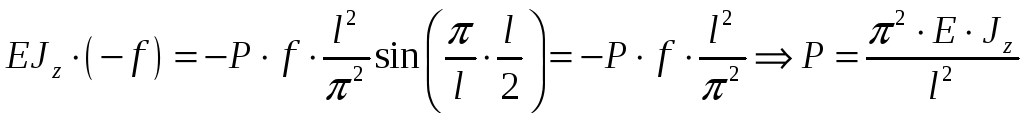
 - критическая сила
для стержня с шарнирными опорами на
концах (формула Эйлера).
- критическая сила
для стержня с шарнирными опорами на
концах (формула Эйлера).
l – длина стержня .

![]() - зависит от способа
закрепления концов стержня и показывает
во сколько раз следует изменить длину
шарнирно закреплённого стержня, чтобы
критическая сила для него была равна
критической силе стержня в данных
условиях закрепления.
- зависит от способа
закрепления концов стержня и показывает
во сколько раз следует изменить длину
шарнирно закреплённого стержня, чтобы
критическая сила для него была равна
критической силе стержня в данных
условиях закрепления.
Значения
![]() для различных способов закрепления
концов стержня.
для различных способов закрепления
концов стержня.
Оба конца закреплены
без шарниров (жёсткое закрепление) -
![]()
Один конец с
шарнирно- закреплён, а другой конец
защемлён -
![]()
Оба конца
шарнирно-закреплены -
![]()
Один конец защемлён
(жёсткое закрепление), а другой свободен
–![]()

Условие устойчивости сжатого стержня.
Устойчивость сжатого стержня считается обеспеченной, если допускаемая сжимающая сила равна:

Под устойчивым прямолинейным равновесием понимается состояние, при котором стержень возвращает свою прямолинейную форму после прекращения действия продольной сжимающей силы.
Неустойчивое прямолинейное равновесие, при котором прямолинейная форма не возвращается после прекращения действия силы.
Критической силой называется такое её минимальное значение, при котором стержень из устойчивого равновесия переходит в неустойчивое.
Формула Эйлера справедлива для случая, когда напряжения, возникающие в стержнях, меньше предела пропорциональности:
![]()
Если значение критической силы разделить на площадь сечения стержня, то получим значение критического напряжения:

Получим:

Гибкость стержня характеризует влияние размеров стержня и способа закрепления его концов и равна отношению приведённой длины стержня к радиусу инерции.
Чем больше гибкость, тем меньше критическое напряжение.
 - значение предельной
гибкости стержня – условие, при котором
формула Эйлера применима.
- значение предельной
гибкости стержня – условие, при котором
формула Эйлера применима.
Когда формула Эйлера не применима, то пользуются формулой Ясинского:


Задача №1: Проверить на устойчивость сжатую стойку, если
![]() .
Длина стойки
.
Длина стойки
l
=3 м,![]() ,
,![]() (Один конец защемлён, жёсткое закрепление,
а другой свободен), в поперечном сечении
стойки прямоугольник с размерами 40 мм
и 80 мм.
(Один конец защемлён, жёсткое закрепление,
а другой свободен), в поперечном сечении
стойки прямоугольник с размерами 40 мм
и 80 мм.


 устойчивость
обеспечена.
устойчивость
обеспечена.
Задача№2: Рассчитать радиус инерции для круга:


Задача№3: Рассчитать радиус инерции для прямоугольника:


Лекция № 7 «Изгиб с растяжением. Косой пространственный изгиб».
До сих пор при рассмотрении изгиба балки предполагалось, что внешние силы, действующие на балку, расположены перпендикулярно продольной оси.
Рассмотрим общий случай, когда изгибающая сила, действующая на балку, расположена наклонно к её продольной оси и принадлежит продольной плоскости.
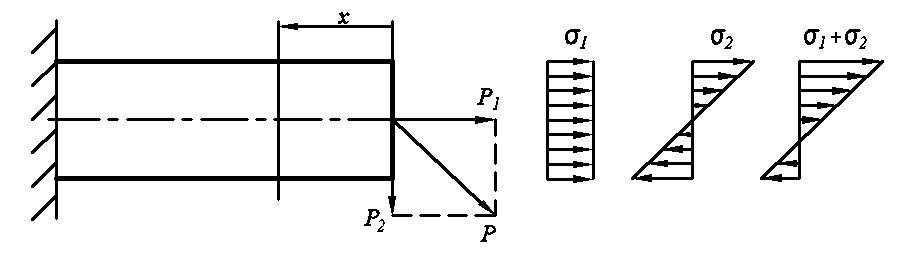
Силу Р,
расположенную под углом, следует
разложить на две составляющие:
![]() .
.
![]() совпадает
с продольной осью и вызывает деформацию
растяжения.
совпадает
с продольной осью и вызывает деформацию
растяжения.
Продольная сила N , возникающая в сечении, равна сумме проекций на продольную ось всех внешних сил, действующих на отсечённую часть
N=![]()
Продольная сила N вызывает нормальные напряжения, направленные от сечения.

![]() вызывает изгиб и нормальные напряжения
вызывает изгиб и нормальные напряжения

Максимальные напряжения при изгибе будут на поверхности. Нормальное напряжение будет положительное на растянутых волокнах, отрицательное – на сжатых. На нейтральном слое, проходящем через центр тяжести сечения, будет равно нулю. На поверхности балки напряжения будут принимать максимальные значения.

Суммарное напряжение будет равно:

Верхние волокна
растягиваются моментом и силой, нижние
сжимаются моментом и растягиваются
силой. На нижних волокнах происходит
компенсация и смещение нейтрального
слоя. Здесь в зависимости от значений
напряжений
![]() возможны три частных случая.
возможны три частных случая.
1.
![]() .
В этом случае нейтральный слой будет
расположен ниже центра тяжести сечения.
.
В этом случае нейтральный слой будет
расположен ниже центра тяжести сечения.
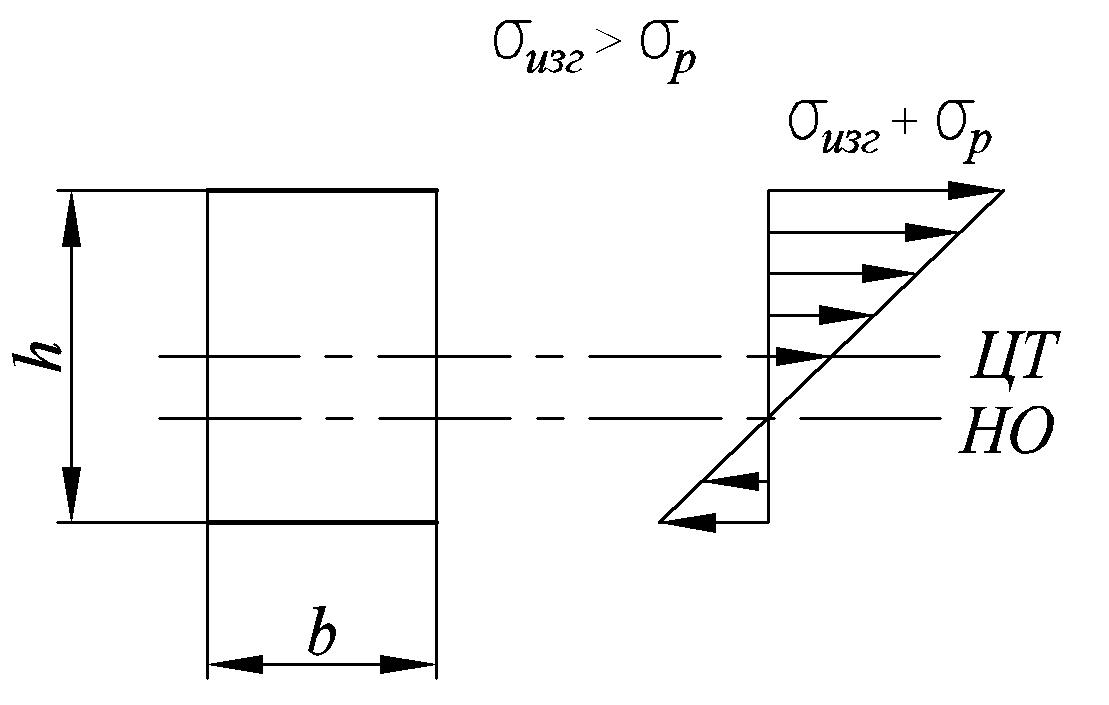
2.
![]() .
В этом случае нейтральный слой будет
расположен на нижней поверхности балки.
.
В этом случае нейтральный слой будет
расположен на нижней поверхности балки.
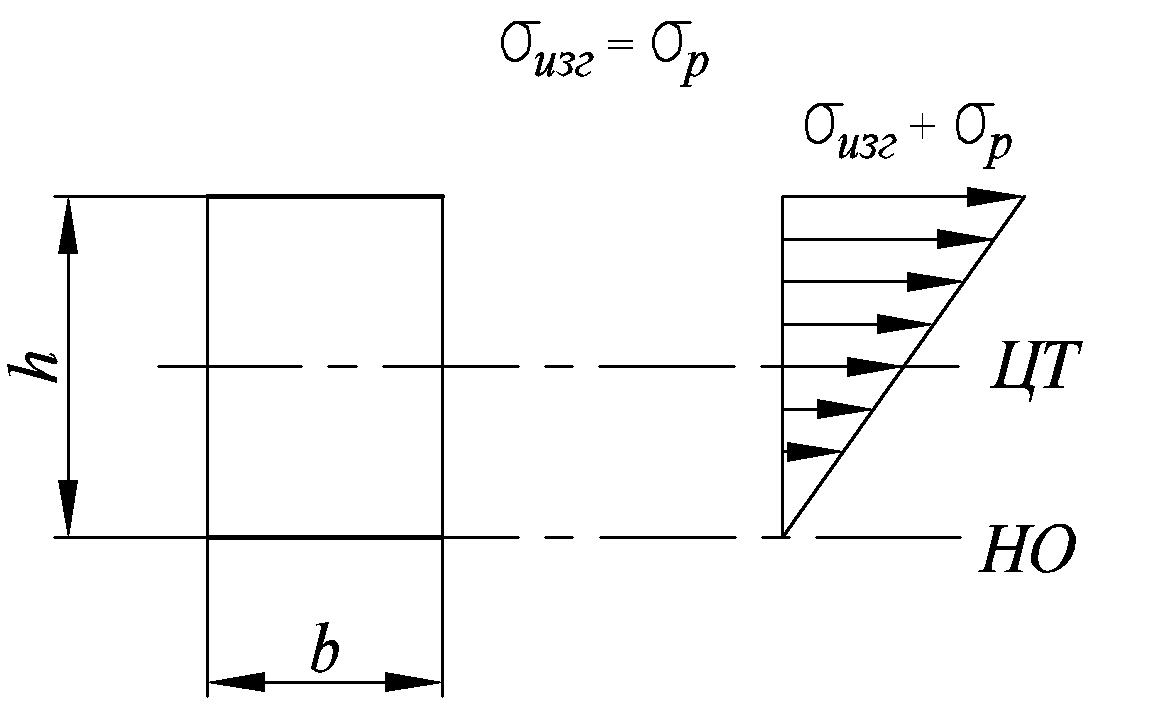
3.
![]() .
В этом случае нейтральный слой будет
за пределами сечения. В сечении
нейтрального слоя не будет.
.
В этом случае нейтральный слой будет
за пределами сечения. В сечении
нейтрального слоя не будет.
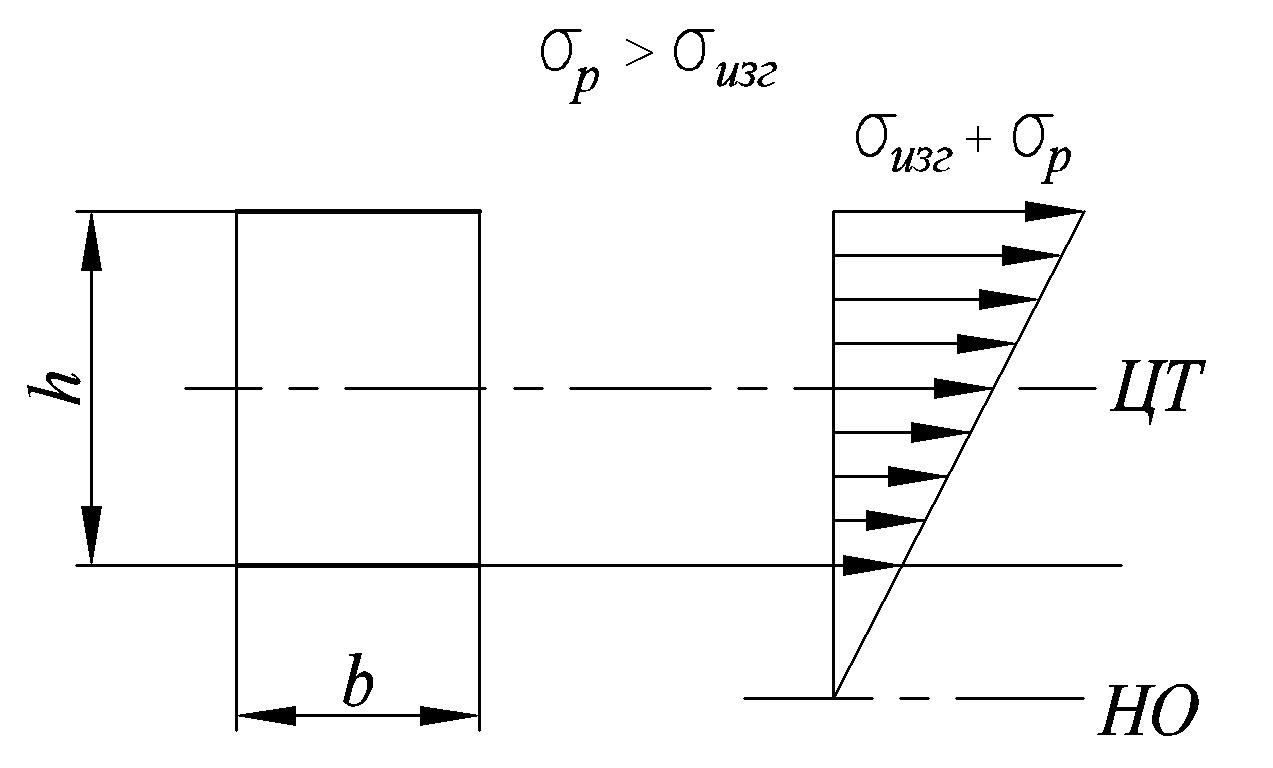
Значения напряжений
![]() будут зависеть от угла наклона силы Р
к продольной оси. От расстояния х
до рассматриваемого сечения будет
зависеть значение
будут зависеть от угла наклона силы Р
к продольной оси. От расстояния х
до рассматриваемого сечения будет
зависеть значение
![]() .
.
При значении угла
![]()
![]() ;
;
При
![]()
![]()
При
![]()
![]() .
.
С увеличением
расстояния
х значение
![]() будет увеличиваться, и поэтому возможен
только 1 случай.
будет увеличиваться, и поэтому возможен
только 1 случай.
Косой пространственный изгиб.
Рассмотрим изгиб, вызываемый силой, не лежащей в плоскости симметрии.

Балка прямоугольного сечения, с защемлённым концом изгибается силой Р, расположенной перпендикулярно продольной оси.
Сечение проводим на расстоянии z от свободной стороны.
Разложим силу Р,
принадлежащую сечению, на две составляющие:
![]()
![]() -
вызывают поперечный изгиб. Косой
пространственный изгиб всегда можно
свести к двум плоским изгибам.
-
вызывают поперечный изгиб. Косой
пространственный изгиб всегда можно
свести к двум плоским изгибам.
Изгибающий момент
от действия силы
![]() будет равен:
будет равен:
![]()
Нормальные напряжения в любой точке, лежащей на расстоянии z от нейтрального слоя, будут равны:

Максимальные нормальные напряжения будут на поверхности при z=b/2 и будут равны:

При этом дальние волокна будут растянуты, ближние сжаты.

Изгибающий момент
от действия силы
![]() будет равен:
будет равен:
![]()
Нормальные напряжения в любой точке, лежащей на расстоянии у от нейтрального слоя, будут равны:

Максимальные нормальные напряжения будут на поверхности при у=h/2 и будут равны:

При этом верхние волокна будут растянуты, нижние сжаты.
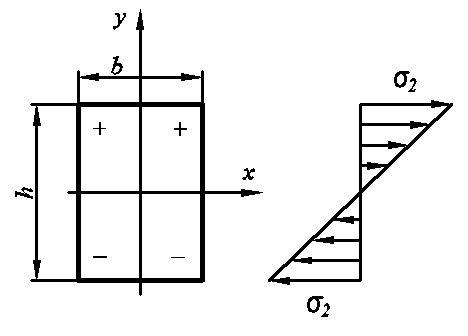
Пользуясь законом
независимого действия сил определим
суммарное максимальное напряжение
изгиба, возникающее при одновременном
действии моментов
![]()


Нейтральная ось проходит через центр тяжести сечения. Точки А и С имеют максимальные значения напряжений. В точке А происходит сжатие, в точке С происходит растяжение.
Лекция № 8 «Внецентренное сжатие».

Внецентренным называется сжатие, когда сила, сжимающая брус, параллельна оси бруса, лежит в одной из его главных плоскостей, но точка её приложения не совпадает центром тяжести сечения.
Эксцентриситетом е называется расстояние от центра тяжести сечения до точки приложения силы. Если к точке центра тяжести сечения приложить уравновешенную систему сил, то действие на брус не измениться.
При этом пара сил будет изгибать брус, сила, приложенная центрально будет сжимать брус.
![]()


Суммарное напряжение будет равно:

Задача: Определить
обеспечена ли прочность при внецентренно
приложенной силе Р=36
Кн, допускаемое
напряжение
![]() .
.


![]()
Модуль суммарного напряжения меньше допускаемого. Прочность обеспечена.
Лекция № 9 «Совместное действие изгиба и кручения. Расчет вала на совместное действие изгиба и кручения».

Окружная сила,
действующая на вал, создает в сечении
крутящий момент
![]() и касательные напряжения
и касательные напряжения

Касательные напряжения расположены в плоскости сечения. Изменяются от нуля в центре до максимального значения на поверхности вала. Максимальные касательные напряжения при кручении расположены на поверхности вала.
Если добавить уравновешенную систему сил, приложенных к центру вала, то пара сил создает крутящий момент, действие которого мы уже рассмотрели. Сила, приложенная к центру, будет изгибать, при этом будут возникать нормальные напряжения:
 ,
,
Площадки выделенного элемента нельзя считать главными, так как действуют касательные напряжения. Можно перейти к главным напряжениям по формулам перехода:
![]()
Эквивалентное напряжение по III гипотезе прочности будет равно:
![]()
Если принять
![]() ,
то
,
то
![]()

Для круглого
поперечного сечения
![]()

Проверочный расчёт:

Проектный расчёт:

Где
![]() - приведённый момент.
- приведённый момент.
Задача: Выполнить проектный расчёт вала – определить d вала при совместном действии изгиба и кручения.
Дано: окружная
сила Р=20 Кн;
диаметр шкива D=400
мм; расстояние
между опорами l=350
мм.; допускаемое
напряжение
![]() .
.

Решение:
Определим крутящий
момент

Определим опорные
реакции
![]()
Определим максимальное значение изгибающего момент:

Зная изгибающий и крутящий моменты, расположенные в разных плоскостях, определим по теореме Пифагора суммарный приведённый момент:
![]()
Проектный расчёт диаметра вала:

Вопросы для проверки уровня знаний.
-
Какой изгиб называется чистым?
-
Какой изгиб называется поперечным?
-
Что называется консолью?
-
Какой метод используется при определении изгибающего момента и перерезывающей силы?
-
Какие существуют дифференциальные зависимости при изгибе между интенсивностью равномерно-распределённой нагрузки, поперечной силой и изгибающим моментом?
-
Чем можно измерить прогиб балки?
-
Как проверить правильность построения эпюр поперечной силы и изгибающего момента?
-
Когда знак изгибающего момента считается положительным, когда – отрицательным?
-
Когда поперечная сила, расположенная в сечении положительная, когда – отрицательная?
-
Запишите закон Гука при изгибе? Что называется жёсткостью сечения при изгибе?
-
Какой слой называется нейтральным. Каковы его свойства?
-
Какая характеристика называется кривизной нейтрального слоя?
-
Запишите приближённое дифференциальное уравнение упругой линии балки.
-
Запишите формулу Журавского. Поясните значения величин, входящих в формулу.
-
Перечислите способы определения перемещений.
-
Запишите формулу определения перемещения методом Верещагина.
-
Какие существуют граничные условия? В каком способе определения перемещений они применяются?
-
Запишите формулу Симпсона-Корнаухова.
-
Какие площадки выделенного элемента называются главными. Каким образом при этом распределяются главные напряжения?
-
Какие гипотезы прочности применяются в настоящее время?
-
Запишите формулу Эйлера. Поясните значения, входящих в формулу, величин.
-
В каком случае формула Эйлера применима?
-
В каком случае применима формула Ясинского?
-
Какой вид расчёта называется проверочным?
-
Какой вид расчёта называется проектным?
-
Какие деформации будут возникать при внецентренном сжатии?
-
Какой момент называется приведенным?
