фадеева

Глава 1. Элементы комбинаторного анализа

из пяти цифр. Каково максимальное число возможных попыток угадать пароль?

Задача 6. Сколькими способами можно расположить на шахматной доске две ладьи так, чтобы одна не могла взять другую? (Одна ладья может взять другую, если она находится с ней на одной горизонтали или на одной вертикали шахматной доски.)

Задача 7. Сколькими способами можно расположить на полке 10 томов энциклопедии?

Задача 8. Сколькими способами можно расположить на полке 10 томов энциклопедии так, чтобы девятый и десятый тома рядом не стояли?

Задача 9. Группу из 10 человек требуется разбить на две непустые подгруппы. Сколькими способами это можно сделать?

Задача 10. Группу из 10 человек требуется разбить на две подгруппы так, чтобы в первой группе было 6 человек, а во второй — 4 человека. Сколькими способами это можно сделать?

Задача 11. Группу из 16 человек требуется разбить на 3 подгруппы, в первой из которых должно быть 5 человек, во второй — 7, в третьей — 4 человека. Сколькими способами это можно сделать?

Задача 12. Сколько существует двузначных чисел, кратных либо 2, либо 5, либо тому и другому числу одновременно?

Задача 13. Из врачебной бригады в 14 человек ежедневно в течение 7 дней назначают двух дежурных врачей. Каково количество различных расписаний дежурства, если каждый врач дежурит только один раз?

Задача 14. Сколько четырехзначных чисел, составленных из нечетных цифр, содержит цифру 3 (цифры в числах не повторяются)?

Задача 15. Шесть групп занимаются в шести расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы 1 и 2 находились бы в соседних аудиториях?

Задача 16. Восемь мешков постельного белья доставляют на 5 этажей гостиницы. Сколькими способами можно распределить мешки по этажам? В скольких вариантах на пятый этаж доставлен один мешок?

Задача 17. Два наборщика должны набрать 16 страниц текста. Сколькими способами они могут распределить эту работу между собой?

15

Раздел 1. Теория вероятностей

Задача 18. Поезд метро делает 16 остановок. Сколькими способами могут распределиться между этими остановками 100 пассажиров, вошедших в поезд на конечной остановке?

Задача 19. Акционерноесобраниекомпаниивыбираетиз50человек президента компании, председателя совета директоров и 10 членов совета директоров. Сколькими способами это можно сделать?

Задача 20. Из фирмы, в которой работают 10 человек, пятеро сотрудников должны уехать в командировку. Сколько может быть составов этой группы, если директор фирмы, его заместитель и главный бухгалтер одновременно уезжать не должны?

Задача 21. В телевизионной студии работают 3 режиссера, 4 звукорежиссера, 5 операторов, 7 корреспондентов и 2 музыкальных редактора. Сколькими способами можно составить съемочную группу, состоящую из одного режиссера, двух операторов, одного звукорежиссера и двух корреспондентов?

Задача 22. Из группы в 25 человек необходимо выбрать старосту и трех членов студкома. Сколькими способами это можно сделать?

Задача 23. Шесть студентов следует распределить по трем группам второго курса. Сколькими способами это можно сделать?

Задача 24. Лифт останавливается на семи этажах. Сколькими способами могут распределиться между этими этажами шестеро пассажиров, находящихся в кабине лифта?

Задача 25. Восемь авторов должны написать книгу из 16 глав. Сколькими способами можно распределить материал между авторами, если два человека напишут по три главы, четыре — по две и два — по одной главе книги?

Задача 26. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, не содержащие одинаковые цифры. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.

Задача 27. Сколько существует пятизначных телефонных номеров, в которых есть цифры 1 и 2?

Задача 28. Семь яблок и три апельсина надо положить в два пакета так, чтобы в каждом пакете был хотя бы один апельсин и чтобы количество фруктов в них было одинаковым. Сколькими способами это можно сделать?

Задача 29. Байт — это единица информации, состоящая из восьми бит, каждый бит равен либо 0, либо 1. Сколько символов можно закодировать с помощью байта?

16

Глава 1. Элементы комбинаторного анализа

Задача 30. Автомобильный номер состоит из трех букв и трех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?

Задача 31. Садовник в течение трех дней должен посадить 10 деревьев. Сколькими способами он может распределить работу по дням , если будет сажать не менее одного дерева в день?

Задача 32. Из ящика, в котором лежат 10 красных и 5 зеленых яблок, выбирают одно красное и два зеленых яблока. Сколькими способами это можно сделать?

Задача 33. Десяти ученикам выданы два варианта контрольной работы. Сколькими способами можно рассадить учеников в два ряда, чтобы у сидящих рядом не оказалось одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?

Задача 34. Группу из 24 студентов (12 девушек и 12 юношей) требуется разбить на две равные подгруппы так, чтобы в каждой подгруппе юношей и девушек было поровну. Сколькими способами это можно сделать?

Задача 35. Группа, состоящая из 27 человек, пишет контрольную работу из трех вариантов (каждый вариант — по 9 человек). Сколькими способами можно выбрать 5 человек из группы так, чтобы среди них оказались писавшие все три варианта?

Задача 36. Лифт, в котором поднимаются 9 пассажиров, останавливается на 10 этажах. Пассажиры выходят группами по 2, 3 и 4 человека. Сколькими способами это может произойти?

Задача 37. Сколькими способами можно расположить группу из 10 человек в ряд так, чтобы между двумя студентами А и Б оказалось два человека?

Задача 38. Предложены 3 билета в различные театры. Сколькими способами они могут быть распределены среди 25 студентов, если каждый из них может получить только один билет?

Задача 39. На группу из 25 человек выделены 3 пригласительных билета на вечер. Сколькими способами они могут быть распределены (не более одного билета в руки)?

Задача 40. Имеются 7 билетов: 3 — в один театр, 4 — в другой. Сколькими способами они могут быть распределены между студентами группы из 25 человек?

ГЛАВА 2

Классическая вероятностная модель. Геометрическая вероятность

К

§ 1. Пространство элементарных исходов

Каждый эксперимент заканчивается каким-то определенным результатом, который не всегда можно предугадать заранее. Для того чтобы формально описать некоторый эксперимент, сделует указать все возможные варианты результатов, которыми этот эксперимент может закончиться. В теории вероятностей такие результаты называются исходами. Множество Ω всех возможных

исходов эксперимента называется пространством элементарных исходов. Предполагается, что эксперимент может закончиться одним и только одним элементарным исходом. В наиболее простом случае все эти исходы можно перечислить:

Ω = {ω1 , ω2, ... ωN} или Ω = {ω1, ω2 , ...}.

Такое пространство элементарных исходов называется дискретным.

Простейшим пространством элементарных исходов является такое пространство, в котором все указанные исходы рассматриваемого эксперимента:

1)равновозможны;

2)взаимно несовместны (т.е. в результате эксперимента может произойти один и только один из указанных исходов);

3)все исходы образуют полную группу событий (т.е. никакие другие исходы, кроме перечисленных, не могут произойти).

Такое пространство конечно и называется пространством равновозможных исходов (или симметричным пространством).

18

Глава 2. Классическая вероятностная модель...

ПРИ М Е Р 1. При бросании симметричной монеты возможны два исхода: выпадение решки или герба. Они удовлетворяют всем трем указанным выше условиям, поэтому в данном случае пространство элементарных исходов представляется в виде (Р и Г – решка и герб соответственно):

Ω= {Ð,Ã }.

ПРИ М Е Р 2. При одновременном бросании двух монет исходы представляют собой упорядоченные пары, состоящие из символов Р и Г. Первый элемент этой пары — это результат, выпавший на первой монете, второй элемент — результат, выпавший на второй монете. Очевидно, что таких пар всего четыре:

Ω= {ÐÐ , ÐÃ , ÃÐ , ÃÃ }.

ПРИ М Е Р 3. В случае бросания игральной кости может вы-

пасть любое из чисел 1, 2, 3, 4, 5, 6. Поэтому пространство элементарных исходов Ω = {1, 2, 3, 4, 5, 6}.

ПРИ М Е Р 4. При одновременном бросании двух игральных костей элементарные исходы представляют собой пары (x, y), где x – число очков, выпавшее на первой кости, y — число очков, выпавшее на второй кости. Очевидно, что таких пар всего 36:

Ω= {(x, y) : x = 1, ..., 6, y = 1, ..., 6}.

§2. Событие и его вероятность

Вдискретном пространстве вероятность каждого элементарного исхода считается заданной и обозначается Р(ωi), или просто рi, причем всегда

1) рi ≥ 0 ;

n	∞
2) ∑pi	= 1 (или ∑pi = 1 ),
i =1	i =1

т.е. сумма (конечная или бесконечная) вероятностей всех элементарных исходов равна единице. Элементарные исходы мы называем элементарными событиями.

19

Раздел 1. Теория вероятностей

Событием A Ω называется любое подмножество, состоящее из элементарных исходов пространства элементарных событий Ω. Обычно говорят, что «событие А произошло», если эксперимент закончился одним из элементарных исходов ωi А.

Вероятностью события А называется сумма вероятностей всех

элементарных исходов, входящих в А, т.е. Р(А) = ∑P (Ωi ). Из этого

Ωi A

определения вероятности события следует, что всегда 0 ≤ Р(А) ≤ 1. В случае равновозможных исходов вероятность элементар-

ного события А определяется формулой

P ( A) = m , n

где n =| Ω | — число элементов во множестве Ω, которое обычно называется общим числом исходов, а m =| A | — число элементов во множестве A, называемое числом благоприятствующих исходов.

Событие A , состоящее из всех элементарных исходов, не входящих в А, называется противоположным событием событию А. Оно происходит тогда и только тогда, когда событие A не произошло. Очевидно, что P ( A) + P ( A) = 1. Это равенство используется для вычисления вероятности события А в случае, когда вероятность противоположного события известна или легко может быть найдена, тогда P ( A) = 1 −P ( A).

Таким образом, для вычисления вероятности в каждой задаче важно определить, в чем состоит эксперимент, затем правильно построить соответствующее пространство элементарных событий Ω и выделить в нем требуемое событие A. Затем, используя методы комбинаторики, подсчитать число элементов в Ω и A.

Задача 1. В ящике 5 апельсинов и 4 яблока. Наудачу выбраны 3 фрукта. Какова вероятность того, что все три фрукта — апельсины?

Решение. Элементарными исходами здесь являются выборки, включающие 3 фрукта. Поскольку порядок здесь безразличен, будем считать выборки неупорядоченными (и, разумеется, бесповторными). Общее число элементарных исходов |Ω| равно числу способов выбрать 3 элемента из 9, т.е. числу сочетаний n = C93 . Число благоприятных исходов m = |А| будет равно числу способов выбора трех апельсинов из имеющихся пяти — иными словами, числу сочетаний трех элементов из пяти, т.е. С35 . Тогда вероятность

20

Глава 2. Классическая вероятностная модель...

	P ( A) =	C 3	=	5!	9!		= 0,12 .
		5
		C93		2!3!	3!6!

Задача 2. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым студентом любого числа из заданных равновозможен, найти вероятность того, что у кого-то из троих задуманные числа совпадут.

Решение. Вначале подсчитаем общее количество исходов. Первый из студентов выбирает одно из 10 чисел — n1 = 10 возможностей, второй делает то же самое — n2 = 10 возможностей, наконец, выбор третьего также — n3 = 10 возможностей. Согласно основной теореме комбинаторики, общее число способов будет равно n = n1 × n2 × n3 = 103 = 1000 элементарных исходов.

Аналогично подсчитывается число благоприятствующих исходов. Первый студент может выбрать любое из 10 чисел, второй любое из 9 чисел, а третий студент — любое из оставшихся 8 чисел. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, в силу той же основной теоремы равно m = 10 × 9 × 8 = 720. Остальные случаи (1000 — 720 = 280) характеризуются наличием хотя бы одного совпадения. Следовательно, искомая вероятность совпадения равна Р = 280/1000 = 0,28.

Задача 3. Найти вероятность того, что в восьмизначном числе ровно 4 цифры совпадают, а остальные различны.

Решение. Событие А = {восьмизначное число содержит 4 одинаковые цифры}. Из условия задачи следует, что в числе 5 различных цифр, одна из которых повторяется. Число способов ее выбора равна числу способов выбора одной цифры из 10 цифр, и эта цифра занимает любые 4 места в числе, т.е. число способов равно С 84 . Оставшиеся 4 места занимают различные цифры из неиспользованных 9, а так как число способов зависит от выбора порядка расположения цифр, то число способов выбора четырех цифр равно А 94 . Тогда число благоприятствующих исходов | A |= 10С84А94 . Всего же способов составления восьмизначных чи-

сел |Ω| = 108. Следовательно, искомая вероятность равна

	P =	| A |	=	10C 4 A4		=	8! 9!		1		= 0,021 168 .
					8 9
		| Ω |		108			4!4! 5!		107

21

Раздел 1. Теория вероятностей

Задача 4. Шестеро клиентов случайным образом обратились в 5 фирм. Найти вероятность того, что хотя бы в одну фирму никто не обратился.

Решение. Рассмотрим обратное событие A , состоящее в том, что в каждую из 5 фирм обратился клиент, тогда в какую-то из них обратились два человека, а в остальные 4 фирмы — по одно-

					5 6!
	му клиенту. Таких возможностей | A |= 5× N 6 (2,1,1,1,1) =					.
				1!1!1!1!2!

Всего же способов распределить шестерых клиентов по 5 фирмам

| Ω |= 56. Отсюда	P ( A) =	5 6! 1	= 0,1152 , следовательно,
		1!1!1!1!2! 56

P (A) = 1 − P ( A) = 0,8848.

Задача 5. Среди 25 экзаменационных билетов имеется 5 «счастливых» и 20 «несчастливых». Студенты подходят за билетами по очереди. У кого больше вероятность вытащить «счастливый» билет: у того, кто подошел первым, или у того, кто подошел вторым?

Решение. Пусть «счастливые» билеты имеют номера 1, 2, 3, 4, 5. Обозначим i1 номер билета, взятого первым студентом, i2 — номер билета, взятого вторым студентом, тогда элементарным исходом будет пара (i1, i2), а пространство элементарных исходов

Ω = {(i1, i2 ) : i1 = 1, ..., 25, i2 = 1, ..., 25, i1 ≠i2 },

где все элементарные исходы равновероятны. Событие А = {первый студент взял «счастливый» билет} имеет вид

A = {(i1, i2 ) : i1 = 1, ..., 5, i2 = 1, ..., 25, i1 ≠i2 },

а событие В = {второй студент взял «счастливый» билет}

B = {(i1, i2 ) : i1 = 1, ..., 25, i2 = 1, ..., 5, i1 ≠i2 }.

Каждое из событий А, В содержит | A |=| B |=C51C241 = 120 элементов, а все пространство Ω содержит | Ω |=Ñ251 Ñ241 = 600 элемен-

тов. Следовательно, Р(А) = Р(В) = 1/5.

§ 3. Геометрическая вероятность

Рассмотрим n-мерное вещественное пространство Rn. Пусть в какую-то ограниченную область Ω R n наудачу брошена точка. Слово «наудачу» означает, что в таком эксперименте все точки

22

Глава 2. Классическая вероятностная модель...

области Ω «равновозможны». В этом случае вероятность попадания точки в какую-то подобласть A Ω определяется формулой

P (A) = V ( A) , V (Ω)

где V(A), V(Ω) — n-мерные объемы областей A и Ω соответственно. Здесь элементарными исходами называются точки множества Ω (которое играет роль пространства элементарных исходов), а благоприятствующими исходами — точки множества A.

Задача 6. Точка брошена наудачу на отрезок [0; 2]. Какова вероятность попадания этой точки на интервал [0,5; 1,4]?

Решение. Здесь пространство элементарных исходов весь отрезок Ω [0; 2], а множество благоприятствующих исходов А = [0,5; 1,4], при этом длины этих интервалов равны l(Ω) = 2 и l(A) = = 0,9. Поэтому вероятность попадания брошенной точки в ука-

	занный интервал равна P ( A) =	l(A)	=	0,9	= 0,45 .
		l(Ω)		2

Задача 7. На отрезок [0; 2] брошены наудачу и поочередно две точки. Какова вероятность того, что первая точка лежит правее второй точки?

Решение. Обозначим получившиеся координаты точек через x и y. Элементарным исходом в таком бросании двух точек будет пара (х, у), а пространством элементарных исходов – квадрат Ω = {(x, y) : x, y [0,2]}. Событие A = {первая точка лежит пра-

вее второй точки} равносильно условию x > y, следовательно, A = {(x, y) : x, y [0,2], x > y}, т.е. представляет собой треугольник

(рис. 1). Площади квадрата и треугольника равны S(Ω) = 4 и S(A) = 2 соответственно, поэтому вероятность P ( A) = S ( A) S (Ω) = 2 4 = 0,5 .

y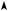

2

0

2

x

Рис. 1.

Задачи для самостоятельного решения

Задача 1. Построить пространство элементарных исходов для эксперимента, в котором монету бросают 3 раза.

23