
- •Міністерство освіти і науки україни
- •§1. Порівняння чисел. Властивості числових нерівностей.
- •§2. Нерівності зі змінними.
- •§3. Місце теми в шкільному курсі математики
- •§4. Основні методи доведення нерівностей
- •4.3. Доведення від супротивного.
- •4.4. Метод математичної індукції
- •4.5. Метод підсилення нерівності.
- •4.6. Методи диференціального числення.
- •§5. Класичні нерівності
- •5.1 Нерівність трикутника
§1. Порівняння чисел. Властивості числових нерівностей.
Порівнювати числа учні вчаться ще у початковій школі. Спочатку вони порівнюють натуральні числа, а потім у 5-6 класах десяткові і звичайні дроби, цілі числа, у 8 класі – дійсні числа. На кожному етапі навчання учні порівнюють числа за певними правилами . Порівняння дійсних чисел має статус означуваної дії.
 Означення
1.
Означення
1.
Число а більше за число b (a>b), якщо різниця а-b – додатне число;
Число а менше за число b (a<b), якщо різниця а-b – від’ємне число;
Якщо різниця а-b дорівнює нулю, то числа а і b рівні (a=b).
Оскільки
різниця чисел а-b
може
бути лише додатною, від’ємною або
дорівнювати нулю, то для довільних чисел
а
і
b
виконується
одне і тільки одне із трьох співвідношень:
 .
Записиa>b,
a<b
називають
числовими нерівностями.
.
Записиa>b,
a<b
називають
числовими нерівностями.
Пригадаємо основні теореми, які виражають властивості числових нерівностей. Доводити їх не будемо, оскільки це загальновідомі факти, які обгруновуються в шкільному курсі математики.
Вл.1
Якщо
 ,
то
,
то
 ;
Якщо
;
Якщо
 ,
то
,
то
 ;
тобто
якщо переставити місцями ліву і праву
частину нерівності, то потрібно поміняти
знак нерівності на протилежний.
;
тобто
якщо переставити місцями ліву і праву
частину нерівності, то потрібно поміняти
знак нерівності на протилежний.
Вл.2
(властивість
транзитивності нерівностей) Якщо
 ,
то
,
то
 .
.
Вл.3
Якщо
 ,
і с – будь-яке число, то
,
і с – будь-яке число, то +с,
тобто, якщо до обох частин нерівності
додати будь-яке дійсне число, то знак
нерівності при цьому не зміниться.
+с,
тобто, якщо до обох частин нерівності
додати будь-яке дійсне число, то знак
нерівності при цьому не зміниться.
Вл.4
Якщо
 ,
і
с – додатне число, то
,
і
с – додатне число, то
 ;
якщо
;
якщо і с – від’ємне
число, то
і с – від’ємне
число, то
 ,
тобто якщо помножити обидві частини
нерівності на додатне число, то знак
нерівності зберігається, на від’ємне
– знак зміниться на протилежний.
,
тобто якщо помножити обидві частини
нерівності на додатне число, то знак
нерівності зберігається, на від’ємне
– знак зміниться на протилежний.
Вл.5
Якщо
 і
і ,
то
,
то
 ,
тобто нерівності з однаковими знаками
можна почленно додавати, зберігаючи
при цьому знак нерівності.
,
тобто нерівності з однаковими знаками
можна почленно додавати, зберігаючи
при цьому знак нерівності.
Вл.6
Якщо

 ,
то
,
то ,
тобто дві нерівності з протилежними
знаками можна почленно віднімати ,
залишаючи при цьому знак тієї нерівності,
від якої віднімається
друга нерівність.
,
тобто дві нерівності з протилежними
знаками можна почленно віднімати ,
залишаючи при цьому знак тієї нерівності,
від якої віднімається
друга нерівність.
Вл.7
Якщо
 і
і ,
де
a,b,c,d
– додатні
числа, то
,
де
a,b,c,d
– додатні
числа, то
 ,
тобто нерівності з однаковими знаками
і з додатною лівою і правою частиною,
можна почленно множити, зберігаючи при
цьому знак нерівності.
,
тобто нерівності з однаковими знаками
і з додатною лівою і правою частиною,
можна почленно множити, зберігаючи при
цьому знак нерівності.
Наслідок
1.
Якщо
 ,
деa
і b
– додатні числа, то
,
деa
і b
– додатні числа, то
 ,n
– натуральне число, тобто обидві частини
нерівності з додатною лівою і правою
частиною можна підносити до одного і
того ж самого степеня з натуральним
показником, не змінюючи при цьому знак
нерівності.
,n
– натуральне число, тобто обидві частини
нерівності з додатною лівою і правою
частиною можна підносити до одного і
того ж самого степеня з натуральним
показником, не змінюючи при цьому знак
нерівності.
Наслідок
2.
Якщо
 ,
деa
і b
– додатні числа, то
,
деa
і b
– додатні числа, то
 ,n
– натуральне число,тобто з обох частин
нерівності з додатною лівою і правою
частинами можна добути арифметичний
корінь одного і того самого степеня, не
змінюючи при цьому знак нерівності.
,n
– натуральне число,тобто з обох частин
нерівності з додатною лівою і правою
частинами можна добути арифметичний
корінь одного і того самого степеня, не
змінюючи при цьому знак нерівності.
Вл.8
Якщо
 і
і ,
де
a,b,c,d
– додатні
числа, то
,
де
a,b,c,d
– додатні
числа, то
 , тобто нерівності з протилежними знаками
з додатною лівою і правою частинами
можна почленно поділити, залишаючи при
цьому знак тієї нерівності, яку ділили
на другу нерівність.
, тобто нерівності з протилежними знаками
з додатною лівою і правою частинами
можна почленно поділити, залишаючи при
цьому знак тієї нерівності, яку ділили
на другу нерівність.
§2. Нерівності зі змінними.
Окрім числових нерівностей, в математиці розглядають нерівності зі змінними. Дамо одне з можливих означень нерівності зі змінними.
Означення 2.
 Запис
Запис
 >
> (1)
(1)
(або
 <
< ),
де
),
де
 і
і

аналітично задані функції з областю визначення відповідно
 називають
нерівністю з n
змінними,
а множину
називають
нерівністю з n
змінними,
а множину
 областю
визначення цієї нерівності.
областю
визначення цієї нерівності.
У записі (1) крім знаків : “>” (більше), “<” (менше) можуть вживатися знаки “≥” (більше або дорівнює; не менше), “≤” (менше або дорівнює; не більше). Нерівності, що містять знаки “>” або “<” називаються строгими, а нерівності, що містять знаки “≥” або “≤” , називаються нестрогими.
Наприклад:
x + y + z –xy - yz - zx ≤ 1, x; y; z
 [0; 1]–
нерівність з трьома змінними
[0; 1]–
нерівність з трьома змінними
x; y; z, областю визначення якої є [0; 1].
 ,
де
,
де
 –
нестрога
нерівність
з
трьома змінними a,
b,
c
і
областю
визначення
–
нестрога
нерівність
з
трьома змінними a,
b,
c
і
областю
визначення
 .
.m2+2n2+2mn+6n+10>0 - строга нерівність з двома змінними m і n. Для неї область визначення не вказується. Однак, знаючи, що многочлен m2+2n2+2mn+6n+10 визначений для всіх дійсних чисел m і n, можна вважати, що область визначення цієї нерівності – всі дійсні числа
Задачі, пов’язані з нерівностями зі змінними бувають двох типів:
на розв'язування нерівностей;
на доведення нерівностей.
Розглянемо
множину
 .
Набір чисел
.
Набір чисел із
множини D,
при
яких нерівність (1) перетворюється в
правильну числову нерівність, називається
розв’язком нерівності (1).
із
множини D,
при
яких нерівність (1) перетворюється в
правильну числову нерівність, називається
розв’язком нерівності (1).
Розв'язати
нерівність
(1) — ознaчaє знайти множину її розв’язків
 .
Множина
.
Множина може бути і порожньою. Тоді кажуть, що
нерівність (1) розв’язків не має.
може бути і порожньою. Тоді кажуть, що
нерівність (1) розв’язків не має.
Довести
нерівність
(1)— означає переконатися, що вона
перетворюється в правильну числову
нерівність при всіх допустимих значеннях
змінних з області
 або з області, яка вказується заздалегідь.
або з області, яка вказується заздалегідь.
Наприклад:
Довести, що для невід’ємних чисел a і b має місце нерівність
 . Тут область
. Тут область вказується в умові.
вказується в умові.Довести, що
 Оскільки
область визначення не вказана, то нею
буде множина всіх дійсних чисел, бо
ліва і права частина нерівності –
функції, визначені для всіх дійсних
значень змінних a,
b,
c.
Оскільки
область визначення не вказана, то нею
буде множина всіх дійсних чисел, бо
ліва і права частина нерівності –
функції, визначені для всіх дійсних
значень змінних a,
b,
c.
Під час розв'язування нерівностей зі змінними важливе значення має поняття рівносильності нерівностей.

Означення 3.
Дві нерівності
 )
<
)
<
 (2)
(2)
і
 (3)
(3)
називаються рівносильними, якщо множини їх розв’язків – рівні,
тобто

Рівносильними вважаються також нерівності, множини розв’язків яких – порожні.
Приклад 2.
Нерівності
 і
і
 >0
рівносильні , бо множина розв’язків
кожної з них визначається так:
>0
рівносильні , бо множина розв’язків
кожної з них визначається так:

Нерівності
 і
і
 не є рівносильними , оскільки значення
х=-1 є розв’язком другої нерівності ,
але не є розв’язком першої.
не є рівносильними , оскільки значення
х=-1 є розв’язком другої нерівності ,
але не є розв’язком першої.Нерівності
 і
і теж рівносильні, оскільки множини їх
розв’язків – порожні.
теж рівносильні, оскільки множини їх
розв’язків – порожні.
Встановлюючи рівносильність нерівностей, найчастіше використовують наступні твердження.
Теорема
1. Нерівності
 і
і - рівносильні.
- рівносильні.
Теорема
2. Нерівності
 і
і - рівносильні.
- рівносильні.
Теорема
3. Нерівності
 і
і - рівносильні, якщо функція
- рівносильні, якщо функція визначена
на ОДЗ нерівності f(
визначена
на ОДЗ нерівності f( )>
g(
)>
g( ).
).
Наслідок
3. Нерівності
f( )>g(
)>g(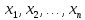 )і
f(
)і
f( )+а>g(
)+а>g( )+a
-рівносильні
для
будь-якого
числа а.
)+a
-рівносильні
для
будь-якого
числа а.
Теорема
4.
Якщо
функція
h( )додатна
при всіх значеннях
)додатна
при всіх значеннях
 з
ОДЗ нерівності f(
з
ОДЗ нерівності f( )>g(
)>g( ),тоді
нерівність f(
),тоді
нерівність f( )>g(
)>g( )і
нерівність
)і
нерівність
 рівносильні.
Якщо функція h(
рівносильні.
Якщо функція h(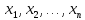 )від’ємна
при всіх значеннях
)від’ємна
при всіх значеннях
 з
ОДЗ нерівності f(
з
ОДЗ нерівності f( )>g(
)>g( ),тоді
нерівність f(
),тоді
нерівність f( )>g(
)>g( )і
нерівність h(
)і
нерівність h( )f(
)f( )<h(
)<h( )g(
)g( )рівносильні.
)рівносильні.
Наслідок
4. Якщо а
– додатне
число, то нерівність f( )>g(
)>g( )
-рівносильна
нерівності аf(
)
-рівносильна
нерівності аf( )>аg(
)>аg( );а
якщо а
–
від’ємне число, то нерівність f(
);а
якщо а
–
від’ємне число, то нерівність f( )>g(
)>g( )
- рівносильна нерівності аf(
)
- рівносильна нерівності аf( )<аg(
)<аg(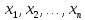 ).
).
Теорема
5. Нерівності
 і
f(
і
f( )
g
(
)
g
( )>0
- рівносильні.
)>0
- рівносильні.
Теорема
6. Якщо функції f( )
і g(
)
і g( )
невід’ємні на цій нерівності
)
невід’ємні на цій нерівності
 та
та
 , де
, де - рівносильні.
- рівносильні.
Теорема
7. Нерівності
 та
та
 ,
де
,
де
 рівносильні.
рівносильні.
Теорема
8. Нерівності
 і
і
 ,
де
,
де
 рівносильні.
рівносильні.
Справедливість цих тверджень випливає з відповідних властивостей числових нерівностей.
Під час доведення нерівностей зі змінними користуються поняттям еквівалентності нерівностей.
Означення 4.
 Дві
нерівності
Дві
нерівності
 (4)
(4)
 (5)
(5)
називаються еквівалентними на непорожній множині М, якщо вони
правильні при всіх значеннях змінних з множини М.
Для
позначення еквівалентності вживається
знак «
![]() ». Наприклад (4)
». Наприклад (4)![]() (5).
(5).
Термін еквівалентність з латинської: «аequus» - рівний, рівноцінний і «valentis» – той, що має силу, грунтовний.
Наприклад:
нерівності:
 і
і 0
-
еквівалентні для всіх значень змінних
x і
y.
Оскільки вираз
0
-
еквівалентні для всіх значень змінних
x і
y.
Оскільки вираз
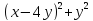 набуває тільки невід’ємних значень.
Отже при будь-яких значеннях змінних
х та у є правильною нерівність
набуває тільки невід’ємних значень.
Отже при будь-яких значеннях змінних
х та у є правильною нерівність .
.
Сформулюємо найважливіші теореми про еквівалентні переходи при доведенні нерівностей зі змінними.
Теорема
9. Нерівності
 і
і
 еквівалентні.
еквівалентні.
Теорема
10. Нерівності
 і
і еквівалентні.
еквівалентні.
Теорема
11. Нерівності
f( )>g(
)>g( )і
f(
)і
f( )+а>g(
)+а>g( )+aеквівалентні
для
будь-якого
числа а.
)+aеквівалентні
для
будь-якого
числа а.
Теорема
12. Якщо а
– додатне
число, то нерівність f( )>g(
)>g( )еквівалентна
нерівності аf(
)еквівалентна
нерівності аf( )>аg(
)>аg( );а
якщо а
–
від’ємне число, то нерівність f(
);а
якщо а
–
від’ємне число, то нерівність f( )>g(
)>g( )
еквівалентна нерівності аf(
)
еквівалентна нерівності аf( )<аg(
)<аg( ).
).
