4.3. Доведення від супротивного.

Суть методу: припускаємо що істинна протилежна рівність і доводимо її суперечність за допомогою рівносильних перетворень.

Приклад 7. Довести, що якщо , то

. (7)

Доведення. Припустимо що існує набір для якого справджується нерівність

Застосовуючи рівносильні перетворення отримаємо наступне:

Що протирічить нерівності Коші. Отже правильна початкова нерівність.

Приклад 8. Довести, що якщо , то

. (8)

Доведення. Припустимо що існує набір для якого справджується нерівність

Застосовуючи рівносильні перетворення отримаємо наступне:

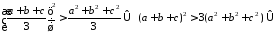
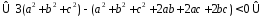
Остання нерівність є невірним, так як сума квадратів не може бути від’ємним числом. Значить і невірне наше припущення, отже справедлива початкова нерівність.

4.4. Метод математичної індукції

Принцип (аксіома) математичної індукції полягає в тому, що твердження, яке залежить від натурального числа n, справедливе для будь-якого, якщо виконуються дві умови:

а) твердження справедливе при (базис індукції);

б) при будь-якому натуральному зі справедливості твердження для(припущення індукції) випливає його справедливість і для (індукційний крок).

На цьому принципі будується метод доведення тверджень, що називається методом математичної індукції. Доведення методом математичної індукції складається з двох частин: у першій частині доводять (перевіряють) істинність твердження при , у другій частині припускають, що твердження правильне при, і доводять справедливість його при(індукція вгору). Існує варіант методу, коли зі справедливості твердження для(припущення індукції) випливає його справедливість і для(індукція вниз).

Приклад 9. Доведіть нерівність для будь-якого натурального n>7.

Доведення.

1. При n=7 маємо:

тобто нерівність правильна.

2. Припустимо, що нерівність виконується при , тобто має місце нерівність

Тоді маємо:

Оскільки очевидно, що при. На основі принципу математичної індукції робимо висновок, що початкова нерівність справджується для будь-якого натурального.

Розглянемо одну з форм доведення методом математичної індукції, яка відрізняється від попередньої.

Нехайі— числові послідовності. Якщо для деякого натурального числаS справедлива нерівністьі для всіхсправедлива нерівністьто для всіхсправедлива нерівність.

Дещо видозміненою формою доведення методом математичної індукції є наступна. Якщо для деякого натурального числа S справедлива нерівністьі для всіхсправедлива нерівністьто для всіхсправедлива нерівність.

Приклад 10. Доведіть нерівність.

Доведення. Розглянемо дві послідовності , де.

1. Нехай , тодіі, очевидно,.

2. Нехай , тоді

3. Доведемо, що тобто доведемо таку нерівність:

Замінимо цю нерівність рівносильною, виконавши тотожні перетворення

Остання нерівність, очевидно, справедлива, тому й вихідна нерівність правильна.

4.5. Метод підсилення нерівності.

Нехай потрібно довести . Тоді використовують допоміжні нерівності ітоді за законом транзитивності

Приклад 11. Довести для довільних

Доведення. Припустимо що нерівність доведена. Виконаємо рівносильні перетворення:

Запишемо нерівність Коші:

За законом транзитивності що і потрібно було довести.