Решетки. Диаграмма Хассе.

Решеткой называют алгебраическую структуру, заданную конечным множеством M с двумя бинарными операциями.

- решетка.

Отношение является отношением частичного порядка.

Множество M с отношением частичного порядка называется упорядоченным множеством.

Для графического представления упорядоченного множества используют диаграмму Хассе.

Каждому элементу ставится в соответствие точка на плоскости, причем если выполняется соответствие , точку, соответствующую элементу a, располагают ниже точки, соответствующей элементу b.

Точки a и b соединены линией или ребром, если

Пусть имеется отношение порядка

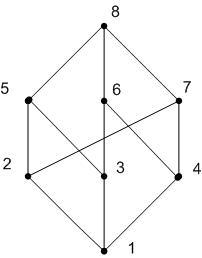
Диаграмма Хассе помогает лучше понимать взаимосвязь элементов, принадлежащих одному и тому же упорядоченному множеству.

Дистрибутивная решетка.

Решетка называется дистрибутивной решеткой, если для всех элементов, принадлежащих множеству M, выполняется условие:

1)

2)

Диаграмма Хассе для дистрибутивной решетки

Булева алгебра.

Булева алгебра - ограниченная дистрибутивная решетка, в которой имеется унарная операция дополнения на множестве М такое, что

;

.

Тема 5. Поля Галуа и их применение. Классическая теория Галуа. Расширения полей и их классификация. Сепарабельные и нормальные расширения. Расширения полей q, f_q, c(t).

5.1 Поля Галуа и их применение

Полеммы называем непустое множествоPкомплексных чисел, обладающее следующими свойствами:

1. если и, тои;

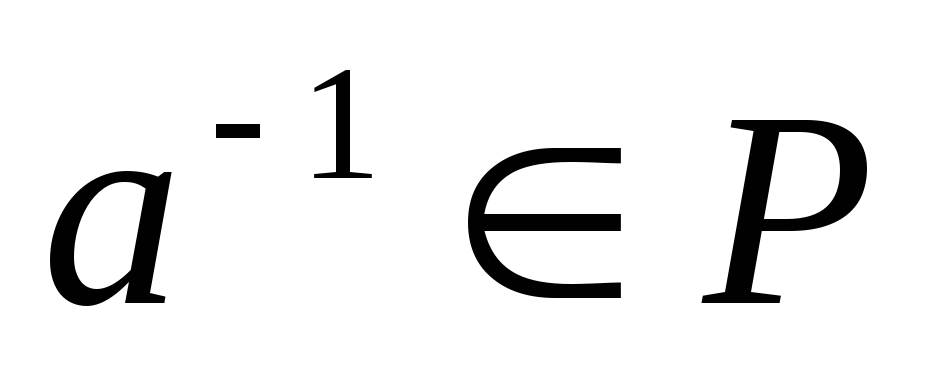2. если , то-и(при).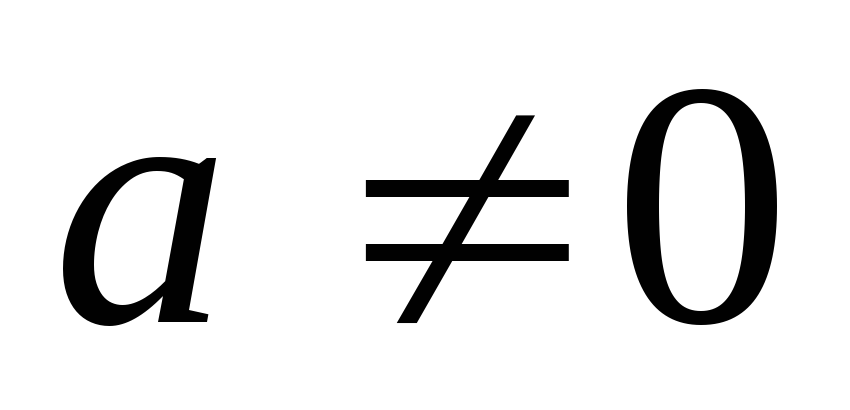

Полями являются, например, поле рациональных чисел R, поле действительных чиселD, поле комплексных чисел С.

Поле Галуаили Конечное поле — поле, состоящее из конечного числа элементов. Конечное поле обычно обозначаетсяили GF(q), где q — число элементов поля. Простейшим примером конечного поля является—кольцовычетов по модулюпростого числа.

Свойства:

Характеристикаконечного поля являетсяпростымчислом.

• Число элементов любого конечного поля есть его характеристика в натуральной степени: .

• Для каждого простогочисла p инатуральногоn существует конечное поле из q = pn элементов, единственное с точностью доизоморфизма. Это поле изоморфно полюразложениямногочлена.

• В каждом поле существует по крайней мере один примитивный элемент α, то есть такой, что . Любой ненулевой элемент β является некоторой степенью примитивного элемента:.

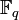• Мультипликативнаягруппаконечного поляявляетсяциклической группойпорядка q − 1. Поэтому, в частности, в конечном поле всегда существует примитивный элемент α, порядок которого равен q − 1, то есть αq − 1 = 1 идля 0 < i < q − 1.

• Поле содержит в себе в качестве подполятогда и только тогда, когда k является делителем n.

Примеры

• , где p — простое: и так далее.

• , где —главный идеалкольца, порожденный неприводимым многочленомстепени n.

Построение

Существует два варианта построения, в зависимости от количества элементов поля, которое необходимо построить:

• Поле содержит p элементов, где p — простое.

Кольцо вычетов по модулю n в случае простого n = p не имеетделителей нуляи являетсяполем.

Элементы — числа. Операции проводятся как с обычными целыми числами с приведениемпо модулюp.

• Поле содержит q = pn элементов, где p — простое, n — натуральное.

Кольцоявляется полем тогда и только тогда, когда многочлен f(x)неприводимнад полем. При этом, где m = deg(f). Таким образом, для построения поля из q = pn элементов достаточно отыскать многочлен степени n, неприводимый над полем, и определитькак указано выше.

Элементами поля являются все многочлены степени меньшей n с коэффициентами из. Операции (сложение и умножение) проводятся по модулю многочлена f(x), то есть результат соответствующей операции — это остаток от деления на f(x) с приведением коэффициентовпо модулюp.

Пример построения поля GF(9)

Пусть надо построить поле GF(9) = GF(32). Для этого необходимо найти многочлен степени 2, неприводимыйв. Такими многочленами являются: x²+ 1

x2 + x + 2

x2 + 2x + 2

2x2 + 2

2x2 + x + 1

2x2 + 2x + 1

Возьмём, например, x2 + 1, тогда искомое поле есть . Если вместо x2 + 1 взять другой многочлен, то получится новое поле, изоморфное старому.

Таблица сложения в GF(9)

+	0	1	2	x	x+1	x+2	2x	2x+1	2x+2
0	0	1	2	x	x+1	x+2	2x	2x+1	2x+2
1	1	2	0	x+1	x+2	x	2x+1	2x+2	2x
2	2	0	1	x+2	x	x+1	2x+2	2x	2x+1
x	x	x+1	x+2	2x	2x+1	2x+2	0	1	2
x+1	x+1	x+2	x	2x+1	2x+2	2x	1	2	0
x+2	x+2	x	x+1	2x+2	2x	2x+1	2	0	1
2x	2x	2x+1	2x+2	0	1	2	x	x+1	x+2
2x+1	2x+1	2x+2	2x	1	2	0	x+1	x+2	x
2x+2	2x+2	2x	2x+1	2	0	1	x+2	x	x+1

Таблица умножения в GF(9):

×	0	1	2	x	x+1	x+2	2x	2x+1	2x+2
0	0	0	0	0	0	0	0	0	0
1	0	1	2	x	x+1	x+2	2x	2x+1	2x+2
2	0	2	1	2x	2x+2	2x+1	x	x+2	x+1
x	0	x	2x	2	x+2	2x+2	1	x+1	2x+1
x+1	0	x+1	2x+2	x+2	2x	1	2x+1	2	x
x+2	0	x+2	2x+1	2x+2	1	x	x+1	2x	2
2x	0	2x	x	1	2x+1	x+1	2	2x+2	x+2
2x+1	0	2x+1	x+2	x+1	2	2x	2x+2	x	1
2x+2	0	2x+2	x+1	2x+1	x	2	x+2	1	2x

5.2 Классическая теория Галуа

Тео́рия Галуа́— разделалгебры, изучающий симметрии корнеймногочленов. Симметрии описываются в терминахгруппы перестановоккорней многочлена (группа уравнения) — термин, впервые использованныйЭваристом Галуа

Созданная Э. Галуа теория алгебраических уравненийвысшихстепеней с одним неизвестным, т. е. уравнений вида

        

         устанавливает условия сводимости решения таких уравнений к решению цепи др. алгебраических уравнений (обычно более низких степеней). Т. к. решением двучленного уравнения xm= Аявляется радикал,то уравнение (*) решается в радикалах, если его можно свести к цепи двучленных уравнений. Все уравнения 2-й, 3-й и 4-й степеней решаются в радикалах. Уравнение 2-й степениx² + px + q = 0было решено в глубокой древности по общеизвестной формуле

        

         уравнения 3-й и 4-й степеней были решены в 16 в. Для уравнения 3-й степени вида x³ + px + q = 0(к которому можно привести всякое уравнение 3-й степени) решение даётся т. н. формулой Кардано:

        

         опубликованной Дж. Карданов 1545, хотя вопрос о том, найдена ли она им самим или же заимствована у др. математиков, нельзя считать вполне решенным. Метод решения в радикалах уравнений 4-й степени был указан Л.Феррари.

         В течение трёх последующих столетий математики пытались найти аналогичные формулы для уравнений 5-й и высшихстепеней. Наиболее упорно над этим работали Э.Безуи Ж.Лагранж. Последний рассматривал особые линейные комбинации корней (т. н резольвенты Лагранжа), а также изучал вопрос о том, каким уравнениям удовлетворяют рациональные функции от корней уравнения (*). В 1801 К.Гаусссоздал полную теорию решения в радикалах двучленного уравнения видаxn= 1, в которой свёл решение такого уравнения к решению цепи двучленных же уравнений низших степеней и дал условия, необходимые и достаточные для того, чтобы уравнениеxn= 1 решалось в квадратных радикалах. С точки зрения геометрии, последняя задача заключалась в отыскании правильных n-угольников, которые можно построить при помощи циркуля и линейки; поэтому уравнениеxn= 1 и называется уравнением деления круга. Наконец, в 1824 Н.Абельпоказал, что общее уравнение 5-й степени (и тем более общие уравнениявысшихстепеней) не решается в радикалах. С другой стороны, Абель дал решение в радикалах одного общего класса уравнений, содержащего уравнения произвольно высоких степеней, т. н. абелевых уравнений.

         Т. о., когда Галуа начал свои исследования, в теории алгебраических уравнений было сделано уже много, но общей теории, охватывающей все возможные уравнения вида (*), ещё не было создано. Например, оставалось: 1) установить необходимые и достаточные условия, которым должно удовлетворять уравнение (*) для того, чтобы оно решалось в радикалах; 2) узнать вообще, к цепи каких более простых уравнений, хотя бы и не двучленных, может быть сведено решение заданного уравнения (*) и, в частности, 3) выяснить, каковы необходимые и достаточные условия для того, чтобы уравнение (*) сводилось к цепи квадратных уравнений (т. е. чтобы корни уравнения можно было построить геометрически с помощью циркуля и линейки). Все эти вопросы Галуа решил в своём «Мемуаре об условиях разрешимости уравнений в радикалах», найденном в его бумагах после смерти и впервые опубликованном Ж. Лиувиллем (См. Лиувилль) в 1846. Для решения этих вопросов Галуа исследовал глубокие связи между свойствами уравнений и групп (См.Группа) подстановок, введя ряд фундаментальных понятий теории групп. Своё условие разрешимости уравнения (*) в радикалах Галуа формулировал в терминах теории групп. Г. т. после Галуа развивалась и обобщалась во многих направлениях. В современном понимании Г. т. — теория, изучающая те или иные математические объекты на основе их групп автоморфизмов (так, например, возможны Г. т. полей, Г. т. колец, Г. т. топологических пространств и т. п.).

3. Расширение полей и их классификация

Расшире́ние Галуа́ — алгебраическое расширение поляEÉ K, являющеесянормальнымисепарабельным. При этих условиях E будет иметь наибольшее количествоавтоморфизмовнад K (если E -конечно, то количество автоморфизмов также конечно и равно степени расширения [E:K]).

Группа автоморфизмов E над K называется группой Галуа и обозначается Gal(E/K) (или G(E/K)).

Если Gal(E/K) абелева,циклическаяи т.д., то расширение Галуа называется соответственно абелевым, циклическим и т.д. соответственно.

Иногда рассматривают группу Галуа для расширения E, которое сепарабельно, но необязательно нормально. В этом случае под группой Галуа E/K понимают группу Gal(Ē/K), где Ē — минимальное нормальное расширение K, содержащее E (в конечном случае, когда сепарабельное расширение является простым E=K(α) для некоторого α, являющегося корнем неприводимогонад K многочлена f(x), Ē являетсяполем разложенияэтого многочлена).

Поля Галуа.

Согласно определению, полем называется множество, на котором заданы операции сложения и умножения, причём выполняются групповые аксиомы (см. теорию групп; должно быть обеспечено выполнение переместительного закона сложения и умножения, наличие нейтральных элементов относительно сложения и умножения).

Говоря обычным языком, для любых элементов должны выполняться равенства a+b=b+aиa*b=b*a. И должен существовать такой элемент е, принадлежащий нашему множеству (полю), что для всех элементов множестваaвыполняетсяa=a+e, и такой элементu, чтоa=a*u. Для обычного сложенияe=0, аu=1.

Однако, умножение и сложение, которые определены для полей, могут не иметь ничего общего с обычным сложением или умножением (кроме выполнения вышеупомянутых законов).

Полями Галуа называются поля, в которых присутствует конечное число элементов. Поле Галуа с количеством элементов NобозначаетсяGF(N).

Определим сложение, как операцию «исключающее ИЛИ» (XOR). Очевидно, что в таком случае, операция сложения является обратной самой себе. Операция умножения в двоичном виде будет выглядеть так

x0011

0011

---------------

+ 00110

0011

---------------

0101

Т.е. обычное умножение «столбиком» со сложением определённым как XOR.

Такую операцию часто представляют как умножение полиномов. (x+1)*(x+1) =x²+1

Можно определить также операцию деления чисел (или полиномов) с остатком - по аналогичным правилам, например:

1100111100000 / 100011101

100011101

-------------

100000110

100011101

--------------

11011000

Число 11011000 (или полином x⁷+x⁶+x⁴+x³) является остатком от деления.

Теперь рассмотрим поле Галуа, состоящее из 2⁴ = 16 элементов. Операция сложения для этого поля определена какXOR, операция же умножения дополнена получением остатка по некоторому модулю.

Выберем в качестве модуля полином x⁴+x+1 (т..е число 10011).

Возьмём единицу и будем последовательно умножать её на 2 и рассмотрим числа, которые будут при этом получаться: (рассмотрим двоичную форму и представление в виде полинома)

1 = 2⁰ = 0001 = x⁰

2⁰*2 = 2¹ = 0010 mod 10011 =2 = x¹

2¹*2 = 2² = 0100 mod 10111 =4 = x²

2²*2 = 2³ = 1000 mod 10011= 8 = x³

Эти три строки повторяют обычное умножение, однако дальше всё не так просто

2⁴*2 = 2⁴ = 10000 mod 10011 = 0011 = 3 = x+1

10011

--------

00011

2⁴*2 = 2⁵ = 100000 mod 10011 = 0110 = 6 = x²+x

10011

----------

000110

и т.д.

составим таблицу умножения

Степень	Результат
0	1	0001
1	2	0010
2	4	0100
3	8	1000
4	3	0011
5	6	0110
6	12	1100
7	11	1011
8	5	0101
9	10	1010
10	7	0111
11	14	1110
12	15	1111
13	13	1101
14	9	1001
15	1	0001

Таким образом, 2¹⁵= 1 и, как нетрудно догадаться, при дальнейшем умножении весь цикл повторится снова. Полученные «степени двойки» несложно умножать между собой, например, 13 * 15 = 2¹³* 2¹² =2¹²⁺¹³= 2^{25 mod 15}= 2¹⁰= 7

Тот же результат, разумеется, можно получить умножив 13 на 15 по описанным правилам по модулю 10011

1111

1101

-----

1111

1111

1111

----------

1001011 mod10011

10011

-------

0111 = 7

Важным фактом является то, что в этой таблице в колонке «результат» повторились все числа от 1 до 15. Если задуматься, то из этого следует, что операция умножения обратима: в самом деле, раз a¹³*a¹²=a¹⁰, тоa¹⁰/a¹²=a^-2+15=a¹³

Таким образом, операция деления может быть выполнена так: находим в таблице «логарифм» - то есть «в какую степень нужно возвести 2 чтобы получить нужное число» - для делимого и делителя, после этого вычитаем логарифм делителя из логарифма делителя и прибавляем 15 (чтобы получить положительное число) и возводим 2 в эту степень.

Наша таблица обладает таким свойством не случайно; это обусловлено выбором основания 2 и модуля 10011. При выборе другого модуля и основания этого вполне могло и не получиться! Число 2 называется в данном случае «примитивным элементом поля». Формализуя, можно сказать что примитивный элемент поля Галуа GF(p) – это такое числоa, что для любыхt<p-1 иs<p-1a^t<>a^s

Таким образом, построенное поле Галуа задаёт правила арифметики для чисел от 0 до 15 (т.е. для двоичных 4-разрядных чисел). В качестве сложения и вычитания используется XOR, умножение выполняется описанным выше способом и операция умножения всегда обратима, т.е. для любое число всегда без остатка делится на другое число (кроме 0: на 0 делить нельзя).

Все дальнейшие наши действия будут подразумевать применение такой арифметики над полями Галуа.

Аналогичным образом можно построить и арифметику для 256-битовых чисел – например, с помощью полинома x⁸+x⁴+x³+x²[phone])

Несмотря на то, что арифметика «странная», для неё можно выводить формулы, аналогичные формулам обычной арифметики. Что и будет делаться ниже.

Теория Галуа

Теория Галуа́— раздел алгебры, изучающий симметрии корней многочленов. Симметрии описываются в терминах группы перестановок корней многочлена (группа уравнения) — термин, впервые использованный Эваристом Галуа.

Приложение к классическим задачам

Теория Галуа даёт единый элегантный подход к решению таких классических задач как

Какие фигуры можно построить циркулем и линейкой?

Какие алгебраические уравнения разрешимы с помощью стандартных алгебраических операций (сложение, вычитание, умножение, деление и извлечение корня)?

Симметрии корней.

Симметрии корней — такие перестановки на множестве корней многочлена, для которых любому алгебраическому уравнению с рациональными коэффициентами, которому удовлетворяют корни, удовлетворяют и переставленные корни.

Пример: квадратное уравнение

У многочлена второй степени a x² + b x + c имеются два корня x1 и x2, симметричных относительно точки x=-b/2a. Возможны два варианта:

Если эти корни рациональны, то уравнению x-x1=0 удовлетворяет только один корень, и группа уравнения тривиальна.

Если корни иррациональны, то группа содержит один нетривиальный элемент x1x2, и изоморфна Z/2Z.

Более сложный пример.

Рассмотрим теперь многочлен. -24

Его корни:

Существует 4!=24 различных перестановки корней этого уравнения, но не все они являются симметриями. Элементы группы Галуа должны сохранять любые алгебраические уравнения с рациональными коэффициентами.

Одно из таких уравнений — a+d=0. Поскольку a+c≠0, перестановка a→a, b→b, c→d, d→c не входит в группу Галуа.

Кроме того, можно заметить, что (a+b)²=8, но (a+c)²=12. Поэтому перестановка a→a, b→c, c→b, d→d не входит в группу.

Окончательно можно получить, что группа Галуа многочлена состоит из четырёх перестановок:

(a, b, c, d) → (a, b, c, d)

(a, b, c, d) → (c, d, a, b)

(a, b, c, d) → (b, a, d, c)

(a, b, c, d) → (d, c, b, a)

и является четверной группой Клейна, изоморфной (Z/2Z)(Z/2Z).

Формулировка в терминах теории полей

Теория полей даёт более общее определение группы Галуа.

Пусть есть основное поле K и многочлен Р К [x]. Рассмотрим алгебраическое расширение L поля K корнями многочлена. Тогда группа Галуа многочлена это группа автоморфизмов поля L, оставляющих элементы поля K на месте.

В классической теории Галуа в качестве основного поля используется поле рациональных чисел Q.

Разрешимые группы и решение уравнений в радикалах

Решения полиомиального уравнения P(x)=0 выражаются в радикалах тогда и только тогда, когда группа уравнения разрешима.

Для уравнения n-й степени в общем виде группа Галуа изоморфна симметрической группеSn, то есть состоит из всех возможных перестановок. Поскольку группыSnприn>4 не являются разрешимыми, существуют многочлены степениn, корни которых не представимы в виде радикалов — теорема Абеля-Руффини.