- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •2. Общие теоремы динамики точки
- •1. Элементы теории поля. Поток, дивергенция, ротор вектора. Теорема Гаусса-Остроградского. Теорема Стокса
- •2. Прямолинейные колебания материальной точки
- •2. Движение точки в поле центральных сил. Формулы Бине
- •2. Движение планет. Закон всемирного тяготения.
- •3. Энергетические методы определения перемещений. Теорема Кастилиано. Интеграл Мора. Правило Верещагина.
- •1. Формула Тейлора и ее остаточный член
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Гравитационные волны в идеальной жидкости
- •1. Ряды Фурье. Основные свойства коэффициентов Фурье. Неравенство Бесселя
- •2. Движение несвободной материальной точки. Плоский математический маятник.
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Теорема Вейерштрасса о равномерной сходимости функционального ряда.
- •2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
- •2. Общие теоремы динамики системы
- •3. Устойчивость упругих стержней. Критическая сила
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •2. Принцип возможных перемещений
- •3. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Достаточные условия сходимости ряда Фурье
- •2. Поверхности разрыва внутри идеальных сжимаемых сред. Адиабата Гюгонио
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Определение интеграла Римана и достаточные условия его существования
- •2. Уравнения Лагранжа 2-ого рода
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •2. Канонические уравнения движения системы
- •3. Основы теории пограничного слоя. Уравнения Прандтля
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Вращение абсолютно твердого тела вокруг неподвижной оси. Давление на ось
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Основы теории пограничного слоя
- •1. Группа,поле, кольцо
- •2. Динамические уравнения Эйлера
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •1. Определение и примеры конформных отображений
- •2. Первые интегралы. Проблема 4-го интеграла. Элементарная теория гироскопа
- •3. Модель идеальной жидкости и газа. Интегралы уравнений движения идеальной жидкости. Сопло Лаваля
- •1. Интегральная теорема Коши
- •Доказательство
- •2. Элементарная теория гироскопов. Движение тяжелого твердого тела вокруг неподвижной точки
- •3. Кручение призматических стержней произвольного постоянного поперечного сечения
- •1. Теорема о разложении аналитической функции в ряд Тейлора
- •2. Принцип Остроградского-Гамильтона
- •3. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •1. Теорема о представимости функции рядом Лорана
- •2. Действие удара на тело, вращающееся вокруг неподвижной оси. Центр удара
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Изолированные особые точки аналитических функций и их классификация
- •2. Общие теоремы динамики системы
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задачи Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
- •2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
- •3. Устойчивость упругих стержней. Критическая сила
- •2. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Решение смешанной задачи для уравнения колебаний струны методом Фурье
- •2. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •3. Движение несвободной материальной точки. Плоский математический маятник
- •1. Решение смешанных задач для уравнения теплопроводности методом Фурье
- •2. Динамика относительного движения материальной точки
- •3. Одномерные нестационарные течения газа и их характеристики
- •1. Классическая вероятность. Теоремы сложения и умножения. Формула полной вероятности. Биномиальное, нормальное и пуассоновское распределения
- •2. Движение твердого тела около неподвижной точки. Скорости и ускорения точек тела
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Базовые принципы мкэ в механике деформируемого твёрдого тела
- •1. Кривизна и кручение. Формулы Френе
- •3. Основные понятия и определения мкэ. Определение и свойства матриц жёсткости, упругости, функций формы, градиентов
- •1. Классификация линейных уравнений в частных производных 2-ого порядка. Примеры уравнений основных типов
- •2. Способы генерации конечно-элементных моделей
- •3. Задача о сильном взрыве в газе
- •1. Случайные величины и их полные характеристики. Характеристическая функция случайной величины и ее свойства. Закон больших чисел
- •2. Кручение призматических стержней произвольного постоянного поперечного сечения
- •3. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •1. Линейные однородные ду n-го порядка. Структура общего решения
- •2. Канонические уравнения движения системы
- •1. Уравнения Лапласа и Пуассона. Постановка граничных задач. Фундаментальное решение уравнения Лапласа. Функции Грина
- •2. Движение точки в поле центральных сил. Формулы Бине
- •3. Интегрирование дифференциального уравнения изогнутой оси балки
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Основные этапы решения задач механики в пакетах компьютерной механики (на примере пакетов ansys и nastran)
- •3. Двумерное стационарное движение газа. Уравнение Чаплыгина
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Принцип Остроградского-Гамильтона
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Численные решения систем алгебраических уравнений. Метод исключения. Метод итераций. Теорема о сходимости
- •2. Слоистые течения вязкой жидкости. Течение Пуазейля. Течение под действием силы тяжести
- •3. Движение точки в поле центральных сил. Закон всемирного тяготения
- •1. Численное решение уравнений. Метод итерации, его сходимость. Метод Ньютона, его геометричсексий смысл
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Модель вязкой жидкости. Уравнения Навье - Стокса
- •1. Численное решение оду. Метод Рунге-Кутта
- •2. Принцип возможных перемещений. Уравнение Даламбера-Лагранжа
- •3. Задача о сильном взрыве в газе
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Общие теоремы динамики системы материальных точек
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Трансзвуковые течения. Уравнение Эйлера–Трикоми. Особенности сверхзвукового обтекания тел
- •1. Численное решение оду. Метод Рунге- Кутта
- •2. Методы четвертого порядка точности.
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
Будем рассматривать движение точки относительно системы отсчёта, перемещающейся произвольным образом от-но инерциальной сис-мы отсчёта. Такое движение будем называть относительным.
 -
в НСК
-
в НСК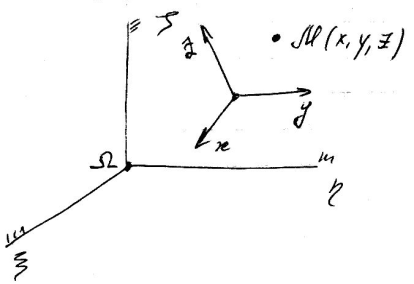
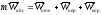
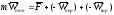
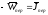 - переносная сила инерции
- переносная сила инерции
 - сила инерции Кориолиса
- сила инерции Кориолиса
 - диф. уравние движения в ПСК.
- диф. уравние движения в ПСК.
Т.е. для того, чтобы составить ДУ в ПСК необходимо к действующим силам добавить переносную силу инерции и силу инерции Кориолиса и далее поступать как обычно.
а) ПСО движется поступательно
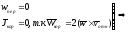
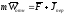
б) ПСО движется поступательно, равномерно и прямолинейно
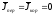 =>
=> - так же инерциальная СО.
- так же инерциальная СО.
в)точка находится в покое от-но ПСК
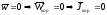
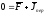 - ур-ние относительного покоя
- ур-ние относительного покоя
Влияние вращения земли на относительный покой и абсолютное движение
а) относительный покой на пов-ти Земли
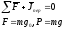
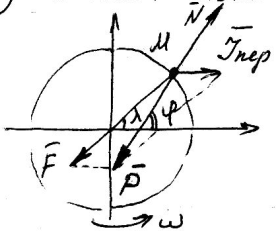
 - геодезическая широта
- геодезическая широта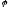 -
астрономическая широта
-
астрономическая широта
![]() - результирующая сила сил тяжести и
переносной инерции
- результирующая сила сил тяжести и
переносной инерции
![]() Составив уравнение проекций на осиOxиOyнайдём связь между
Составив уравнение проекций на осиOxиOyнайдём связь между![]() и
и![]()
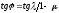 ,
где
,
где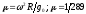

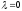 -
экватор
-
экватор![]()
 -
ускорение силы тяжести
-
ускорение силы тяжести
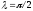 -
полюс
-
полюс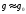
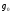 -
ускорение силы притяжения
-
ускорение силы притяжения
б) отклонение падающих тел от вертикали
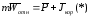
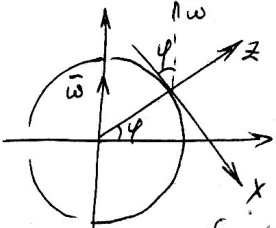
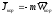
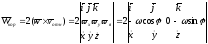
Проектируем (*) на оси Ox,Oy,Oz. ДУ 2-го порядка -> ДУ 1-го порядка. Полученные ДУ решаем методом последовательных приближений . Уже на втором приближении оценим как отклоняется точка от вертикали
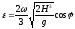 - восточное отклонение для северного
полушария – приH=100м
- восточное отклонение для северного
полушария – приH=100м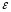 =1.2см
=1.2см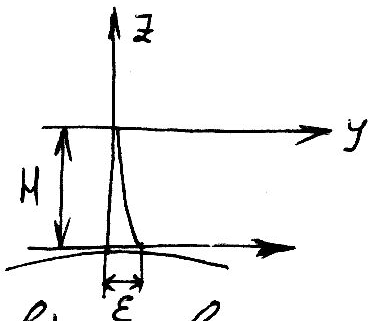
в) влияние вращения Земли на движение тел по горизонтальной пов-ти
рисунок как и в б)
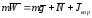
 т.к.
т.к. ,
,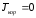 ,
,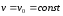
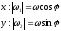
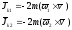

 пл-тиXY=>
пл-тиXY=>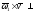 пл-тиXY=>
пл-тиXY=>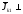 пл-тиXY=>
пл-тиXY=>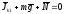
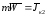
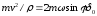 =>
=>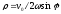 -
точка, движущаяся в горизонтальной
пл-ти, отклоняется в право в северном
полушарии и влево – в южном. Маятник
Фуко
-
точка, движущаяся в горизонтальной
пл-ти, отклоняется в право в северном
полушарии и влево – в южном. Маятник
Фуко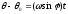 пл-ть поворачивается на
пл-ть поворачивается на в сторону противоположную вращению
земли3.Модель
вязкой жидкости. Уравнения Навье - Стокса
в сторону противоположную вращению
земли3.Модель
вязкой жидкости. Уравнения Навье - Стокса
Опр: жидкость называется вязкой, если в ее объеме при относительном перемещении слоев действуют как нормальные, так и касательные силы напряжения.
Тензор напряжений:
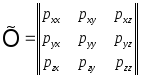
![]() ;
;
![]() -
напряжение на площадке с нормальюx,
в проекции на ось x
(нормальное).
-
напряжение на площадке с нормальюx,
в проекции на ось x
(нормальное). ![]() -
касательное напряжение
-
касательное напряжение
Движение вязкой жидкости описывается уравнениями Навье - Стокса. Уравнения Навье – Стокса получаются из уравнения движения сплошной среды в напряжениях (если вместо компонент тензора напряжений подставить их выражения через компоненты тензора скоростей деформаций из закона Навье-Стокса):
![]() ;
;
![]() -
коэф. динамической вязкости
-
коэф. динамической вязкости
![]() ;
;
![]() -коэф.
объемной вязкости;
-коэф.
объемной вязкости;![]() , μ – коэффициент динамической вязкости,
, μ – коэффициент динамической вязкости,![]() -
коэф. кинемат. вязкости;
-
коэф. кинемат. вязкости;![]()
Для
несжимаемой жидкости
![]() ;
;![]() =>
получаем уравнения Навье – Стокса:
=>
получаем уравнения Навье – Стокса:
![]()
![]()
Проекции на оси координат (еще нужно Fx, Fy и Fz добавить с “+” справа в 1-ых 3-х уравнениях):
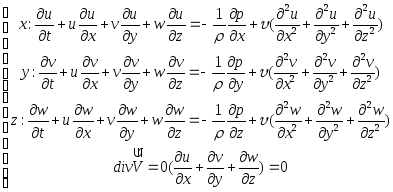
Единственность решения уравнений Навье – Стокса выбирают из начальных и граничных условий.
Граничные условия:
Область течения ограничена твердыми неподвижными стенками, условие полного прилипания, т.е
 на
на ( неподвижная граница),
( неподвижная граница),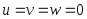
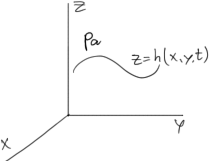
Область течения ограничена подвижными границами, тогда скорость жидкости непосредственно у границы = скорости движения границы
 на
на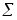
условия на свободной поверхности:
Опр: поверхность свободная - если ее взаимодействия с внешней средой осуществляется по средствам внешнего давления.
Динамические
условия:
![]() на
на![]() +
условие отсутствия касательных
напряжений, т. е
+
условие отсутствия касательных
напряжений, т. е![]() ,
на скорости условия не ставятся.
,
на скорости условия не ставятся.
Скорость точек на
поверхности жидкости = скорости движения
самой поверхности, т.е
![]() - уравнение поверхности
- уравнение поверхности![]()
Условие на поверхности раздела двух жидкостей:
На
поверхности раздела выполняются условия: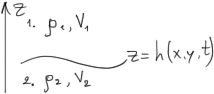
а)
кинематические условия:
![]() при
при![]() ;
;![]() ;
;![]()
b)
динамические условия:
![]() -
равенство сил, т. е
-
равенство сил, т. е![]() ;
;![]()
Билет 15 1. Признаки сходимости знакопостоянных числовых рядов
Для
числ. послед-ти а1,
а2,
…an
, аi
R,
 наз. числ. рядом, аi
-члены ряда.
наз. числ. рядом, аi
-члены ряда.
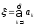 - наз. частичной суммой ряда.
- наз. частичной суммой ряда.
Конечн.или
бесконечн. предел
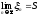 наз. суммой ряда. ЕслиSR,
то ряд сх-ся, если S=
или предел не сущ., то ряд расх.
наз. суммой ряда. ЕслиSR,
то ряд сх-ся, если S=
или предел не сущ., то ряд расх.
Опр.
Ряд
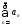 наз. знакопостоянным, если его члены
все одного знака:
наз. знакопостоянным, если его члены
все одного знака:
Признак Коши. Пусть
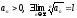 .
Если
.
Если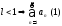 - сх-ся. Если
- сх-ся. Если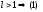 - расход.;l=1
– необходим. дельнейшее исслед-е
- расход.;l=1
– необходим. дельнейшее исслед-еПризнак Даламбера. Пусть
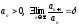 .
если
.
если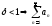 сх-ся,
сх-ся, расх,
расх,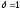 - необх. дальнейш. исслед-е.
- необх. дальнейш. исслед-е.Признак Раабе. Пусть
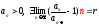 .
Если
.
Если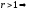 -сх-ся,
-сх-ся,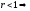 - расх-ся,r
= 1 -- необх. дальнейш. исслед-е.
- расх-ся,r
= 1 -- необх. дальнейш. исслед-е.Признак Гаусса. Пусть
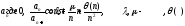 -
огранич., т.е.
-
огранич., т.е.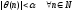 .
Тогда если
.
Тогда если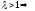 сх-ся,
сх-ся,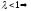 расх-ся,
расх-ся,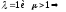 сх-ся,
сх-ся,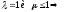 расх.
расх.Интегр. признак. Пусть f – невозраст. (т.е.
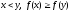 ) неотрицат. ф-я на полуоси
) неотрицат. ф-я на полуоси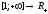 ,
тогда след. усл. эквивалентны:
,
тогда след. усл. эквивалентны:
6) Признаки
сравнения:
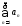 и
и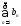 - числовые ряды. Если
- числовые ряды. Если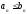 ,
тоa)
из сх-ти р.
,
тоa)
из сх-ти р.
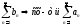 ;
б) из расх-ти р.
;
б) из расх-ти р.