- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •2. Общие теоремы динамики точки
- •1. Элементы теории поля. Поток, дивергенция, ротор вектора. Теорема Гаусса-Остроградского. Теорема Стокса
- •2. Прямолинейные колебания материальной точки
- •2. Движение точки в поле центральных сил. Формулы Бине
- •2. Движение планет. Закон всемирного тяготения.
- •3. Энергетические методы определения перемещений. Теорема Кастилиано. Интеграл Мора. Правило Верещагина.
- •1. Формула Тейлора и ее остаточный член
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Гравитационные волны в идеальной жидкости
- •1. Ряды Фурье. Основные свойства коэффициентов Фурье. Неравенство Бесселя
- •2. Движение несвободной материальной точки. Плоский математический маятник.
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Теорема Вейерштрасса о равномерной сходимости функционального ряда.
- •2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
- •2. Общие теоремы динамики системы
- •3. Устойчивость упругих стержней. Критическая сила
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •2. Принцип возможных перемещений
- •3. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Достаточные условия сходимости ряда Фурье
- •2. Поверхности разрыва внутри идеальных сжимаемых сред. Адиабата Гюгонио
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Определение интеграла Римана и достаточные условия его существования
- •2. Уравнения Лагранжа 2-ого рода
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •2. Канонические уравнения движения системы
- •3. Основы теории пограничного слоя. Уравнения Прандтля
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Вращение абсолютно твердого тела вокруг неподвижной оси. Давление на ось
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Основы теории пограничного слоя
- •1. Группа,поле, кольцо
- •2. Динамические уравнения Эйлера
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •1. Определение и примеры конформных отображений
- •2. Первые интегралы. Проблема 4-го интеграла. Элементарная теория гироскопа
- •3. Модель идеальной жидкости и газа. Интегралы уравнений движения идеальной жидкости. Сопло Лаваля
- •1. Интегральная теорема Коши
- •Доказательство
- •2. Элементарная теория гироскопов. Движение тяжелого твердого тела вокруг неподвижной точки
- •3. Кручение призматических стержней произвольного постоянного поперечного сечения
- •1. Теорема о разложении аналитической функции в ряд Тейлора
- •2. Принцип Остроградского-Гамильтона
- •3. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •1. Теорема о представимости функции рядом Лорана
- •2. Действие удара на тело, вращающееся вокруг неподвижной оси. Центр удара
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Изолированные особые точки аналитических функций и их классификация
- •2. Общие теоремы динамики системы
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задачи Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
- •2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
- •3. Устойчивость упругих стержней. Критическая сила
- •2. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Решение смешанной задачи для уравнения колебаний струны методом Фурье
- •2. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •3. Движение несвободной материальной точки. Плоский математический маятник
- •1. Решение смешанных задач для уравнения теплопроводности методом Фурье
- •2. Динамика относительного движения материальной точки
- •3. Одномерные нестационарные течения газа и их характеристики
- •1. Классическая вероятность. Теоремы сложения и умножения. Формула полной вероятности. Биномиальное, нормальное и пуассоновское распределения
- •2. Движение твердого тела около неподвижной точки. Скорости и ускорения точек тела
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Базовые принципы мкэ в механике деформируемого твёрдого тела
- •1. Кривизна и кручение. Формулы Френе
- •3. Основные понятия и определения мкэ. Определение и свойства матриц жёсткости, упругости, функций формы, градиентов
- •1. Классификация линейных уравнений в частных производных 2-ого порядка. Примеры уравнений основных типов
- •2. Способы генерации конечно-элементных моделей
- •3. Задача о сильном взрыве в газе
- •1. Случайные величины и их полные характеристики. Характеристическая функция случайной величины и ее свойства. Закон больших чисел
- •2. Кручение призматических стержней произвольного постоянного поперечного сечения
- •3. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •1. Линейные однородные ду n-го порядка. Структура общего решения
- •2. Канонические уравнения движения системы
- •1. Уравнения Лапласа и Пуассона. Постановка граничных задач. Фундаментальное решение уравнения Лапласа. Функции Грина
- •2. Движение точки в поле центральных сил. Формулы Бине
- •3. Интегрирование дифференциального уравнения изогнутой оси балки
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Основные этапы решения задач механики в пакетах компьютерной механики (на примере пакетов ansys и nastran)
- •3. Двумерное стационарное движение газа. Уравнение Чаплыгина
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Принцип Остроградского-Гамильтона
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Численные решения систем алгебраических уравнений. Метод исключения. Метод итераций. Теорема о сходимости
- •2. Слоистые течения вязкой жидкости. Течение Пуазейля. Течение под действием силы тяжести
- •3. Движение точки в поле центральных сил. Закон всемирного тяготения
- •1. Численное решение уравнений. Метод итерации, его сходимость. Метод Ньютона, его геометричсексий смысл
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Модель вязкой жидкости. Уравнения Навье - Стокса
- •1. Численное решение оду. Метод Рунге-Кутта
- •2. Принцип возможных перемещений. Уравнение Даламбера-Лагранжа
- •3. Задача о сильном взрыве в газе
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Общие теоремы динамики системы материальных точек
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Трансзвуковые течения. Уравнение Эйлера–Трикоми. Особенности сверхзвукового обтекания тел
- •1. Численное решение оду. Метод Рунге- Кутта
- •2. Методы четвертого порядка точности.
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
2. Канонические уравнения движения системы
Из уравнений Лагранжа
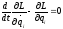 (рассм.сис-му
под действ.потенц.сил)
(рассм.сис-му
под действ.потенц.сил)
Следует ,что обобщ.коорд. и скорости образуют полную систему(2s) переменных.
Рационально перейти от (s) уравнений 2-го порядка к (2s) уравнений 1-го порядка. Такое преобразование было вып. Гамильтоном. Оно привело к новой сис-ме ДУ, кот.наз. кононической, а переменные вход. в него кононическими перем.
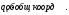 ,
,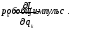 - это конон.переменные.
- это конон.переменные.
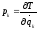 -
для потенциальных сил
-
для потенциальных сил -линейная
ф-я от
-линейная
ф-я от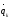 ,
т.к.
,
т.к.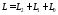
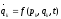
Используем ур.Лагр.2-го
рода
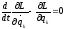
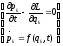
Введём ф-ю Гамильтона
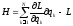 (*)
Т.к. с-ма стационарна , то
(*)
Т.к. с-ма стационарна , то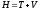 ,
,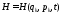
Проварьируем ф.H(рав-во(*))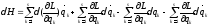
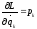
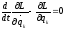 ,
,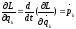

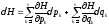
Сравним коэф.при
одинаковых вариациях
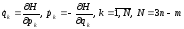 ,m – количество
связей. Получим (2s)
уравнений 1-го порядка, запис в сим.форме
,m – количество
связей. Получим (2s)
уравнений 1-го порядка, запис в сим.форме
3. Основы теории пограничного слоя. Уравнения Прандтля
При
обтекании тел различных форм область
течения можно разбить на 2 подобласти: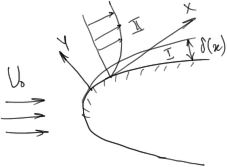
1-влияние трения между стенок существенно
2-можно пренебречь влиянием касательных напряжений, т.е. относительным перемещением слоев и течение можно рассматривать как невязкое.
Опр:
Пограничным слоем называется тонкий
слой вблизи обтекаемого тела. В котором
скорость меняется от 0 на поверхности
тела, до скорости набегающего потока
вне его.
Уравнение пограничного слоя:
Рассмотрим обтекание плоских поверхностей и уравнение получим на основе пластинки.
![]() -скорость
набегающего потока. Рассмотрим плоскую
задачу: (x,y)
-скорость
набегающего потока. Рассмотрим плоскую
задачу: (x,y)
![]()
Основное
предположение: толщина пограничного
слоя
![]()
![]() -размер
пластинки.
-размер
пластинки.
Используем уравнения Навье-Стокса в плоском случае:
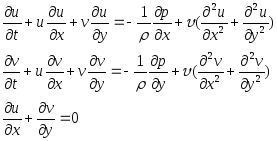
Граничные
условия:
![]() при
при![]() -
условие прилипания.
-
условие прилипания.
![]() т.к. пластинка тонкая,
она не изменяет потока жидкости.
т.к. пластинка тонкая,
она не изменяет потока жидкости.
![]() -
характерная скорость напр. по оси x,
-
характерная скорость напр. по оси x,
![]() -y
, L-
характерный размер
-y
, L-
характерный размер
Сделаем
оценку членов уравнения Навье-Стокса:
![]()
![]()
![]() ;
;
![]() -
из интеграла Бернулли;
-
из интеграла Бернулли;![]()
Из
уравнения неразрывности =>
![]() (*)
(*)
=>
![]() (1)
;
(1)
;![]()
![]() (2) ; отнесем (1) к (2):
(2) ; отнесем (1) к (2):![]() т.е. 1-м членом можно пренебречь
т.е. 1-м членом можно пренебречь
Инерционные
члены имеют одинаковый порядок с вязкими
, если
![]() =>
=>![]()
![]() т.е.
т.е.![]()
1.![]() 2.
2.![]() 2а)
2а)![]() 3.
3.![]() из
(*)
из
(*)
4.![]() -
давление пограничного слоя постоянно
по
-
давление пограничного слоя постоянно
по![]()
![]() ;
;![]() ;
;![]()
![]() ;
;
![]() ;
;![]()
![]() ;
;![]()
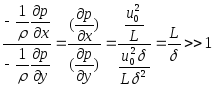 т.е. можно пренебречь
т.е. можно пренебречь
![]()
2-ое
уравнение:
![]() т.е. поперек пограничного слоя давление
не меняется
т.е. поперек пограничного слоя давление
не меняется
В
результате оценок:
![]() - система уравнений Прандтля
- система уравнений Прандтля![]()
Гр.
условия сохраняют свой вид:
![]() при
при![]()
![]() при
при![]()
Задача Блазиуса:
Стационарное
обтекание тонкой пластинки потоком
вязкой жидкости со скоростью
![]()
на бесконечности.
![]()
![]()
![]()
(![]() вне пограничного слоя)
вне пограничного слоя)
Оценки
теории погр-го слоя: 1)
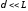 ; 2)
; 2)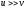 ; 3)
; 3)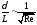 4)
4)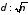 5)
5)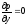
Задача Блазиуса.
Рассмотрим
стационарное обтекание пластинки
потоком вязкой жидкости. Движение
описывается системой Прандтля и
граничными условиями:
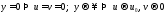 .
.
Данная
задача решается с помощью введения
функции тока
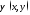 и автомодельной переменной
и автомодельной переменной ;
;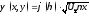
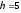 − граница пограничного слоя
− граница пограничного слоя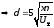
Все расчеты будут справедливы только для ламинарного течения (без перемешивания)
Билет 21
1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
Дана
обл-ть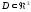 (
(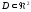 ).
).
Будем
говорить, что в обл задано скалярное
поле, если
 т
т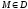 ставится в соотв по известному закону
число
ставится в соотв по известному закону
число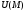 .
Если
.
Если т
т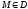 ставится в соотв по известномузакону
некот в-р если
ставится в соотв по известномузакону
некот в-р если ,
то гов-ят, что в обл
,
то гов-ят, что в обл задано векторное поле.
задано векторное поле.
Задание
векторного поля
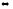 заданию ф-ции
заданию ф-ции ,
а задание скалаярного поля
,
а задание скалаярного поля

Поле
наз диф-мым, если ф-ции
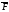 и
и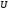 диф в обл
диф в обл .
.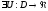 диф скал поле. Тогда в-р
диф скал поле. Тогда в-р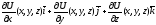 назградиентом
скалярного поля
назградиентом
скалярного поля
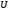 в т
в т .
Обозн
.
Обозн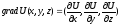
В
данном случае скалярное поле порожд
векторное поле градиента
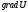 - вектор, кот по напр-ю и своему значению
характеризует скорость возрастания
ф-ции
- вектор, кот по напр-ю и своему значению
характеризует скорость возрастания
ф-ции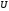 .
.
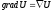 ,
где
,
где
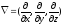 - оператор Гамильтона.
- оператор Гамильтона.
Опр.
 поле
поле
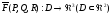 - диф векторное поле, тогда вектор
- диф векторное поле, тогда вектор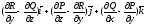 наз ротором векторного поля
наз ротором векторного поля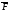 и обозн
и обозн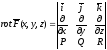
Если
рассм
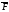 как поле скоростей при движении тв тел,
то с точностью до множителя ротор этого
поля дает угловую скорость.
как поле скоростей при движении тв тел,
то с точностью до множителя ротор этого
поля дает угловую скорость.
Опр.
 поле
поле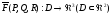 - диф векторное поле, тогда величина
- диф векторное поле, тогда величина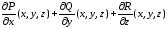 наз дивиргенцией вект поле
наз дивиргенцией вект поле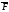 в т
в т и обозн
и обозн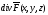 .
.
При
движении несжим жидк при наличии
источников (или стоков) дивергенция
хар-ет плотность источника (стока).
 диф вект поле порождает вект поле его
ротора и скалярное поле его дивергенции.
диф вект поле порождает вект поле его
ротора и скалярное поле его дивергенции.
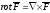 ;
;
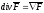
Св-ва.
1)
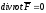 2)
2)
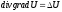 (
(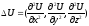 - оп-р Лапласа) 3)
- оп-р Лапласа) 3)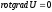
Опр.
 Этот
инт-л наз потоком в-ра
Этот
инт-л наз потоком в-ра ч/з пов-ть
ч/з пов-ть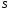 в указ направлении.
в указ направлении.
Теорема Остроградского-Гаусса
Пусть в области Gзаданы функцииP,Q,Rнепрерывные на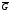 вместе со своими частными производными
тогда
вместе со своими частными производными
тогда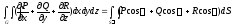
Теорема Стокса.
Рассм
вект поле
 некоторой
кривой
некоторой
кривой .
.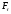 - проекция в-ра
- проекция в-ра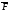 на ед в-р касательной
на ед в-р касательной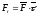
Опр.
![]() лин интл в поле
лин интл в поле
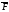 вдоль
вдоль
 .
Если
.
Если замкнута, то инт-л назыв циркуляцией
замкнута, то инт-л назыв циркуляцией
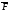 вдоль
вдоль
 .
.
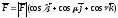 ,
, .
.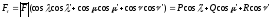
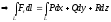 .
.
Если в-р
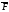 - в-р силы, то этот лие
интеграл
- в-р силы, то этот лие
интеграл
![]() предст собой работу сил поля вдоль
кривой
предст собой работу сил поля вдоль
кривой .
.
Теорема Стокса. Циркуляция
в-ра
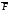 вдоль по контуру
вдоль по контуру
 равно потоку ротора в-ра
равно потоку ротора в-ра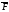 ч/з пов-ть
ч/з пов-ть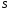 ,
натянутую на эту кривую
,
натянутую на эту кривую
Теорема Стокса (новая).
Циркуляция в-ра
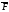 вдоль по контуру
вдоль по контуру
 равно потоку вихря этого поля ч/з пов-ть
равно потоку вихря этого поля ч/з пов-ть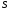 ,
натянутую на эту кривую
,
натянутую на эту кривую