6.3. Дослідження функції на екстремум за допомогою другої похідної
При класифікації екстремальних точок функції y= f (x)можна
використати також її другу похідну.
Розв′язки системи
єточками
максимуму,
а
розв’язки системи
є точками
мінімуму
функції
= f(x).
Таким чином, для знаходження екстремумів функції за допомогою другої похідної треба:
1) знайти стаціонарні точки , тобто точки, в яких перша похідна
дорівнює нулю;
2) обчислити значення другої похідної в одержаних точках;
3) якщо f ′(x0)>0, то в точці x0 маємо мінімум, якщо f ′(x0)<0, то в точці х0 маємо максимум, якщо ж f ′(x0)=0, то відповіді немає і тому слід скористатися першим правилом, тобто знайти екстремум в цій точці за першою похідною.
Відзначимо, що в
сумнівному випадку, коли f
′(x0)=
0 і f
′(x0)=0,
можна також
скористатися більш загальним твердженням:
якщо функція
= f(x)
має в колі
точки х0
неперервні
похідні до n-го
порядку (n>1)
включно і якщо f
′ (x0)=
f
′ (x0)=…=
f
(n-1
)(x0)=0,
в той час як
f
(n)
(x0)
ǂ
0,то при n
непарному функція не має екстремумув
в точці х0
, при n
парному функція має максимум, коли f
(n)(x0)<0,
і мінімум,
коли f
(n)(x0)>0.
6.4 Найменше і найбільше значення функції на відрізку
Відомо, що неперервна на відрізку [a;b] і диференційована в усіх точках цього відрізка функція f(x) досягає свого найбільшого і найменшого значення або в критичних точках, або на кінцях відрізка. Тобто для знаходження найбільшого і найменшого значення функції f(x) на відрізку [a;b] слід керуватися таким правилом:
Знаходимо критичні точки першого роду (не вдаючись в дослідження, чи будуть в них екстремуми функції і якого виду) ;
Обчислюємо значення функції в усіх критичних точках, які належать інтегралу (а; b) і на кінцях відрізка [a; b] ;
Із одержаних значень вибираємо найбільше і найменше. Вони і будуть шуканими.
Розв’язання прикладів
Приклад
1.
Знайти інтервали монотонності функції
=
х2
×
е-х
Розв’язання. Функція визначена на всій числовій осі. ЇЇ похідна
'
(х)
= 2хе-х
+
х2е-х
(-1)
= х(2-х) е -х
Знаходимо
критичні точки першого роду:
' (х) = 0, якщо х = 0 і х = 2,
'
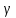(х) ≠ ∞.
Точки
х = 0 і х = 2 ділять числову вісь на три
інтервали: (-∞; 0), (0; 2), (2; +∞).
Оскільки
похідна
' (х) = х(2-х)е-х
є неперервною в інтервалі (-∞; +∞), то
вона зберігає знак в інтервалах (-∞; 0)
і (2; +∞). Значення похідної в точці х = -1
від’ємне,
в точці х = 1
- додатне,
в точці х = 3 від’ємне.
При визначенні знака похідної слід
врахувати , що е-х
> 0,
для будь-яких х. Тому
'
(х)< 0
для всіх х є
( -∞; 0) U
(2; +∞)
і ±
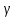'(х)
> 0 для всіх
х є
(0;
2).
Отже функція
=х2е-х
монотонно спадає
в інтервалах (-∞; 0) і (2; +∞) та монотонно
зростає
в інтервалі (0;
2).
Приклад
2.
Знайти інтервали монотонності функції
=2х2-lnx
Розв’язання. Задана функція визначена для х > 0. ЇЇ похідна
'
(х) = 4х -
=
;
Знайдемо точки, в яких ця похідна дорівнює нулю або не існує:
'
(х) = 0, якщо 4х2
–
1 = 0, звідки
х =
±
,
'(х)
= ∞, якщо х = 0.
Оскільки
задана функція визначена для х
> 0, то знак її
похідної
треба визначити лише в інтервалах
(0;
]
і [
;
+∞).
Значення
'(
) <
0, тому
'(х)
<
0 для всіх х є
(0;
),
а це означає, що в інтервалі(0;
)
функція
= 2х2
– lnх
монотонно спадає.
Оскільки
'
(1)> 0, то
'
(х)> 0 для
всіх
х є
(2; +∞) і тому в інтервалі
(2; +∞) задана функція монотонно зростає.
Приклад
3.
Показати, що функція
= arctg
– x
всюди
спадає.
Розв’язання.
Задана функція
визначена для всіх х є
R.
Оскільки її похідна
'
(х) =
-1 =
= -
≤ 0, для всіх х є (-∞; +∞), то ця функція
спадає в усій області визначення.
Приклад
4.
Знайти екстремум функції
= 2х3
-
6х2
– 18х + 7.
Розв’язання. Задана функція визначена і диференційована в інтервалі
(-∞;
+∞). ЇЇ похідна
'
(х) = 6х2
– 12х – 18 = 6(х2
– 2х – 3) = 6(х + 1)(х – 3).
Знайдемо
критичні точки
'
(х) = 0, якщо х = -1 і х = 3,
'
(х) ≠ ∞. В інтервалах ( -∞; -1) і (3; +∞)
похідна
'(х)
додатна, бо
'(-2)
> 0 і
'(4)
> 0,
а в інтервалі [-1;
3]
вона від’ємна,
бо
у'(0) < 0.
Визначимо, які із цих критичних точок є екстремальними (рис. 13)
Обчислюємо значення функції в екстремальних точках, тобто знаходимо шукані екстремуми :
max
= у (-1) = -2 – 6 + 18 + 7 + 17= - 8 +18+24=- 8 + 42 =34,
min
= у (3) = 54 – 54 – 54 + = - 47.
Приклад 5.
Знайти екстремум функції
=x
– ln(1+
x2).
Розв’язання. Задана функція визначена на всій числовій осі, бо 1 + х2 > 0 для будь-яких х. ЇЇ похідна
'
= 1 –
=
=
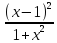≥ 0,
Отже, функція зростає, екстремумів немає.
Приклад 6.
Знайти найбільше і найменше значення
функції
=x4-
2x2
+ 5
на
відрізку [-2 ; 2]
Розв’язання.
Знаходимо
'
= 4x3
– 4x
= 4x(x2
– 1) 
.Знаходимо
критичні точки першого роду :
4x
(x2
- 1 ) = 0
звідки x
= 0
,
x
= - 1, x
= 1
і
'(x)
≠∞.
Відзначимо,
що найдені точки належать відрізку
[-2;2]
Обчислюємо значення функції в критичних точках і на кінцях відрізка:
=4,
=4,
Із одержаних значень вибираємо найменше і нійбільше.
Приклад
7. Знайти
найбільше і найменше значення функції
=
на відрізку [- 6 : 8]
Розв’язання. Діючи, як і в попередньому прикладі, одержимо:
;
=
0 при x
= 0
3)
Приклад 8. Знайти найбільше і найменше значення функції
= x3
– 3x2
+ 6x
- 2 
на відрізку [-1;1].
Розв’язання.
при
будь-яких x
, оскільки D
= - 4 < 0, тому
функція монотонно зростає і, отже,
(-1) = -12
– найменше значення
функції,
(1)
= 2
– найбільше значення
функції.
Приклад 9.
Знайти екстремуми функції 
користуючись
другою похідною.
Розв’язання.
Задана функція визначена для всіх x
.
Диференціюючи її двічі, одержимо:
2
+x2
· 2(a – x)(-1) = 2x(a – x)(a – x – x) = 2x(a – x)(a –
2x) = 2(a2x
– 3ax2
+ 2x3)
2-6ax
+6x2)
Знаходимо
стаціонарні точки, тобто точки, в яких
похідна
Розв’язуючи рівняння матимемо
x
= 0 ; x
=
Обчислимо значення другої похідної в одержаних точках:
2
>0,
2
< 0,
2
> 0.
Таким чином, в
точках 
і
функція
має мінімум, причому
min
= 0
і
в точціx
=
-
максимум, причому
max
=
Приклад 10.
За допомогою другої похідної знайти
екстремуми функції
=
.
Розв’язання.
Діючи далі, як і в попередньому прикладі, знаходимо:
=
;
якщо
звідси
x
= e
– стаціонарна
точка.
Обчислюючи
значення другої похідної при x=e,
маємо:
-1
>0,
отже ( e;
e)
– точка мінімуму.