6.2. Законы распределения непрерывных случайных величин

6.2.1. Равномерное распределение

В некоторых задачах практики встречаются непрерывные случайные величины, о которых известно, что их возможные значения находятся в некотором промежутке, где они одинаково вероятны. О таких случайных величинах говорят, что они распределены по закону равномерной плотности. Из такого понятия следует, что их функция плотности распределения имеет вид

Определим константу С из свойства 4 функции плотности

Легко найти интегральную функцию распределения

и основные числовые характеристики равномерного распределения:

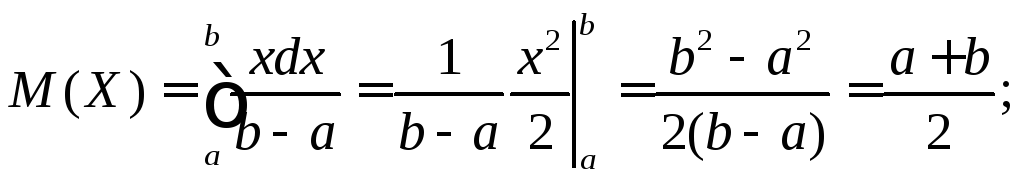
Пример 6.5. Школьник измеряет линейкой длину отрезка до целых значений шкалы (в мм). В этом случае ошибка измерения (случайная величина Х) может принять любое значение в промежутке , т.е. является равномерно распределенной. Найти числовые характерис-тики данной случайной величины Х.

Пример 6.6. Известно, что троллейбусы двигаются с интервалом 5 ми-нут. Студент выходит из корпуса в случайный момент времени. Какова вероятность того, что студент будет ждать троллейбус более 2 минут?

Случайная величина Х  время ожидания троллейбуса имеет равно-мерный закон распределения с функцией плотности распределения:

Поэтому искомая вероятность

Найдем числовые характеристики. данной случайной величины

6.2.2. Показательное распределение

Определение 6.4. Показательным (экспоненциальным) распределением называется распределение, которое имеет функцию плотности вида

с параметром .

Найдём интегральную функцию этого распределения

Приведём графики дифференциальной и интегральной функций.

1

0 х 0 х

Тогда вероятность попадания случайной величины в интервал

Найдем основные числовые характеристики показательного распреде-ления – математическое ожидание

Аналогично, используя формулу интегрирования по частям дважды, находим и дисперсию

т. е. для показательного распределения выполняется соотношение

Показательное распределение широко используется в теории надёжности. Пусть элемент некоторого устройства начинает работать в момент времени , а в моментt происходит отказ в работе. Обозначим через T непрерывную случайную величину – время безотказной работы элемента, а через  интенсивность отказа (среднее число отказов в еди-

ницу времени), тогда функция распределения опре-

деляет вероятность отказа элемента за время t, а функция

(6.1)

вероятность безотказной работы за 1

время t. Она называется функцией

надёжности. Ее график аналогичен

графику функции плотности

показательного распределения . t

Пример 6.7. Случайная величина Т  время безотказной работы станка имеет показательное распределение. Определить вероятность того, что время безотказной работы станка будет не менее 6000 часов, если среднее время безотказной работы станка 4000 часов.

Здесь математическое ожидание

и тогда

Характеристическое свойство закона надежности:

Вероятность безотказной работы устройства на интервале времени длительности t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от времени t.

Действительно, обозначим события:

А – безотказная работа устройства на интервале времени ;

В – безотказная работа устройства на интервале времени ;

А В – безотказная работа устройства на интервале времени .

Найдем вероятности этих событий

Найдем условную вероятность того, что устройство будет работать безотказно на интервале времени при условии, что оно уже проработало безотказно на предыдущем интервале времени

Как видим, полученная формула не содержит , а содержит только величину времениt.

Другими словами, в случае показательного закона распределения прош-лая работа устройства не влияет на вероятность его будущей безотказной работы, что очень удобно для решения практических задач.