§8. Монотонные последовательности. Число

I о пределе монотонной последовательности

Уже известно, что сходящаяся последовательность – ограничена. Однако, не всякая ограниченная последовательность имеет конечный предел: примером может служить последовательность .

Одним из условий, обеспечивающих существование предела, является монотонность ограниченной последовательности.

Теорема.1. Всякая ограниченная монотонная последовательность имеет конечный предел. 2. Всякая неограниченная монотонная последовательность является бесконечно большой (определенного знака).

Заметим, что для убывающей последовательности достаточно доказывать ограниченность снизу, а для возрастающей – ограниченность сверху.

Пример.Рассмотрим последовательность с общим членом. Для доказательства монотонности преобразуем член:

.

Мы получили рекуррентное соотношение

, где.

Члены данной последовательности положительны, а , следовательно,, т.е.убывает. Ее ограниченность снизу очевидна, ибо.

Сформулированная выше теорема обеспечивает существование конечного предела . Для последовательностинетрудно получить:

, т.е..

Теперь перейдем к пределу в обеих частях рекуррентного соотношения, причем в правой части имеем право использовать теорему о пределе произведения (ибо исходящиеся):

или.

Отсюда получаем: .

II Число е

Рассмотрим последовательность с общим членом

и попытаемся применить к ней теорему, сформулированную выше.

Монотонный характер непосредственно не усматривается, так как с возрастанием показателя степениоснование степениубывает. Чтобы убедиться в монотонности, разложим степень по формуле бинома Ньютона:

.

Если теперь от перейти к, т.е. увеличитьна единицу, то, во-первых, добавится еще одно (положительное) слагаемое, а, во-вторых, каждое из уже написанных слагаемых увеличится, ибо множители видазаменятся большими множителями. Отсюда следует, что,

т.е. последовательность возрастающая.

В последнем выражении для опустим все скобки. Тем самым каждое слагаемое увеличится и мы получим оценку:.

Учитывая, что , усилим эту оценку:

.

(Здесь использована формула для суммы геометрической прогрессии). Итак, последовательность возрастает и ограничена сверху, следовательно, она имеет конечный предел. Его обозначают буквой. Это число

имеет исключительную важность, как для самого математического анализа, так и для его приложений.

Лекция 5

§9. Предел функции

I Общее определение

Договоримся о терминологии. Термин «число » означает как обычное число, так и один из символов:или. Термин «точка» означает как конченую точку, так и «бесконечно удаленную»:,или. При этом под окрестностью такой «бесконечно удаленной» точки понимается интервалили объединение этих интервалов соответственно (при произвольном).

Окрестностью же конечной точки понимаем любой интервал, содержащий эту точку. Для простоты формулировок и для бесконечно больших последовательностей будем говорить: «последовательность сходится (к или)».

Рассмотрим функцию , определенную в некоторой окрестности точки(за исключением, быть может, самой точки) и возьмем из этой окрестности последовательность точек

отличных от и сходящуюся к. Значения функции в точках этой последовательности также образуют числовую последовательность

и можно ставить вопрос существования ее предела.

Определение 1 (язык последовательностей). Числоназывают пределом функциив точке(или при) и пишут

(или:при),

если для любой сходящейся к последовательности (1) значений аргумента, отличных от, соответствующая последовательность (2) значений функции сходится к числу.

Геометрический смысл равенства : график функции в окрестности точкиприближается (стремится) к точке.

Пример 1.Вычислим пределв точке. Рассмотрим произвольную последовательностьи. Для соответствующей последовательности значений функцииимеем. Таким образом,.

Пример 2.Покажем, что предел функцииприне существует. Рассмотрим две последовательности значений аргумента с членамии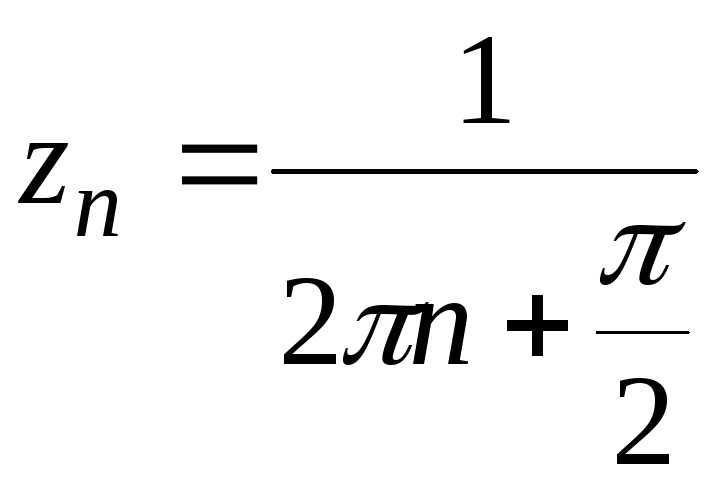. Очевидно, что. При этом для последовательностей значений функции:

,

.

Таким образом, для двух сходящихся к 0последовательностей значений аргумента соответствующие последовательности значений функций имеют разные пределы. А это по определению предела функции и означает, чтоне существует.