
- •Числовые ряды Лекция № 44. Тема 1 : Числовой ряд. Необходимый признак сходимости
- •1.2. Необходимый признак сходимости. Гармонический ряд
- •Лекция № 45
- •2.2. Признак Даламбера
- •2.3. Радикальный признак Коши
- •2.4. Интегральный признак Коши
- •Тема 3 : Знакопеременные ряды
- •3.1. Знакочередующиеся ряды. Теорема Лейбница
- •3.2. Абсолютная и условная сходимость
- •Список литературы
- •С о д е р ж а н и е
Лекция № 45
2.2. Признак Даламбера
Теорема 1.
Пусть для ряда с положительными членами
 сущест-вует конечный или бесконечный
предел
сущест-вует конечный или бесконечный
предел![]() ,
тогда:
,
тогда:
1. Если
![]()
ряд сходится;
ряд сходится;
2. Если
![]()
ряд расходится;
ряд расходится;
3. Если
![]()
ответа на вопрос о сходимости теорема
не даёт. В этом случае требуются
дополнительные исследования.
ответа на вопрос о сходимости теорема
не даёт. В этом случае требуются
дополнительные исследования.
Вначале докажем
пункт 1.
Из определения предела следует:
![]()
![]() выполняется
выполняется![]() или
или![]() .
Если
.
Если
![]() ,
то можно указать такое
,
то можно указать такое![]() ,
для которого выполняется
,
для которого выполняется![]() и тогда
и тогда .
Таким образом,
.
Таким образом,
![]() выполняются равенства:
выполняются равенства:
 .
(1)
.
(1)
Из формул (1) следует,
что ряд
 сходится
сходится![]() .
Тогда по признаку сравнения сходится
и ряд
.
Тогда по признаку сравнения сходится
и ряд .
.
Аналогично
доказывается и случай 2.
Здесь имеем
![]() ,
и выполняется неравенство
,
и выполняется неравенство ,
т.е. нарушается необходимый признак
сходимости, следовательно, ряд
расходится.
,
т.е. нарушается необходимый признак
сходимости, следовательно, ряд
расходится.
Пример 1.
Исследовать сходимость ряда
![]() .
.
Вычислим предел

Пример 2.
Исследовать сходимость ряда
 .
.
Вычислим предел

т.е. ряд расходится.
2.3. Радикальный признак Коши
Аналогично можно доказать следующую теорему.
Теорема 2.
Пусть для ряда с положительными членами
 сущест-вует конечный или бесконечный
предел
сущест-вует конечный или бесконечный
предел![]() ,
тогда:
,
тогда:
1. Если
![]()
ряд сходится;
ряд сходится;
2. Если
![]()
ряд расходится;
ряд расходится;
3. Если
![]()
ответа на вопрос о сходимости теорема
не даёт. В этом случае требуются
дополнительные исследования.
ответа на вопрос о сходимости теорема
не даёт. В этом случае требуются
дополнительные исследования.
Пример 3.
Исследовать сходимость ряда
 .
.
Вычислим предел
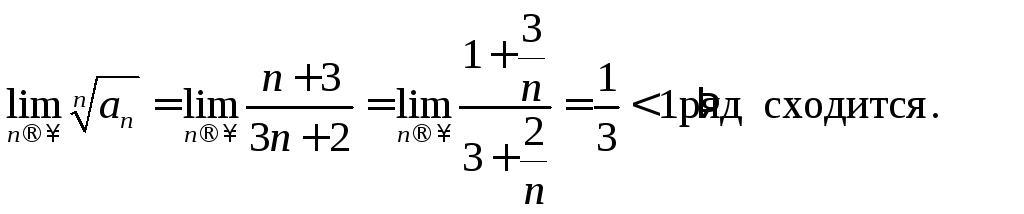
Пример 4.
Исследовать сходимость ряда
 .
.
Вычислим предел

2.4. Интегральный признак Коши
Пусть дан ряд с
положительными членами
 .
.
Заменим в общем
члене ряда
![]() натуральную переменнуюп
вещественной переменной х.
Получим функцию
натуральную переменнуюп
вещественной переменной х.
Получим функцию
![]() ,
для которой
,
для которой![]() .
Исходя из геометрического смысла
определённого интеграла, можно доказать
следующую теорему.
.
Исходя из геометрического смысла
определённого интеграла, можно доказать
следующую теорему.
Теорема 3.
Если функция
![]() непрерывная и невозрастающая на
непрерывная и невозрастающая на![]() ,
тогда:
,
тогда:
1. Если интеграл
 сходится, т.е.
сходится, т.е. ,
то ряд
сходится;
,
то ряд
сходится;
2. Если интеграл
 расходится, то ряд расходится.
расходится, то ряд расходится.
Пример 5.
Исследовать на сходимость ряд
 .
.
Рассмотрим
функцию .
Для нее имеем
.
Для нее имеем

Таким образом,
обобщённый гармонический ряд сходится,
если
![]() и расходится, если
и расходится, если![]() .
Легко убедиться,что
признак
Даламбера не даёт ответа на вопрос о
сходимости этого ряда.
.
Легко убедиться,что
признак
Даламбера не даёт ответа на вопрос о
сходимости этого ряда.
Тема 3 : Знакопеременные ряды
3.1. Знакочередующиеся ряды. Теорема Лейбница
Определение 1. Ряд называется знакопеременным, если среди его членов имеется бесконечное число как положительных, так и отрицательных членов.
Определение 2. Знакопеременный ряд, члены которого имеют чере-дующиеся знаки, называется знакочередующимся рядом.
Такой ряд имеет
вид
![]() ,
где все
,
где все![]() .
.
Теорема Лейбница. Если в знакочередующемся ряде члены ряда удовлетворяют условиям:
1.
![]() ;
;
2.
![]() ,
,
то ряд сходится, и его сумма не превосходит первого члена.
Рассмотрим чётные частичные суммы такого ряда
![]() .
.
Все члены в скобках
положительные, следовательно,
![]() и
и![]() с ростомт.
с ростомт.
Теперь запишем
эту сумму так
![]() .
.
Тогда
![]() ,
т.е. сумма ограничена сверху и при этом
,
т.е. сумма ограничена сверху и при этом![]() .
Тогда по свойству предела она имеет
предел
.
Тогда по свойству предела она имеет
предел![]() ,
причем
,
причем![]() .
.
Покажем теперь,
что и
![]() .
Так как
.
Так как![]() ,
то переходя к пределу в этом равенстве
получим
,
то переходя к пределу в этом равенстве
получим
![]() ,
ч.т.д.
,
ч.т.д.
Замечание 1.
Ошибка, совершаемая при замене S
на
![]() не превосходит по абсолютной величине
первого из отброшенных членов, т.е.
не превосходит по абсолютной величине
первого из отброшенных членов, т.е.![]() ,
так как отброшенные члены также
образуют знакочередующийся ряд.
,
так как отброшенные члены также
образуют знакочередующийся ряд.
Пример 6.
Ряд
![]() сходится, так как удовлетворяет усло-виям
теоремы Лейбница. При этом приближённое
вычисление его суммы будет вычисляться
с точностью
сходится, так как удовлетворяет усло-виям
теоремы Лейбница. При этом приближённое
вычисление его суммы будет вычисляться
с точностью![]() .
.
Пример 7.
Исследовать сходимость ряда
![]() .
.
Замечаем, что
 и тогда по теореме Лейбница
и тогда по теореме Лейбница
1.
![]() ; 2.
; 2.![]() ,
т.е. ряд сходится.
,
т.е. ряд сходится.
