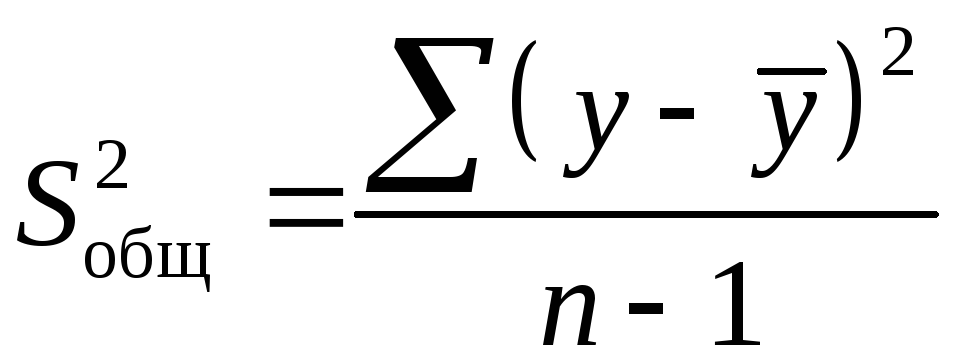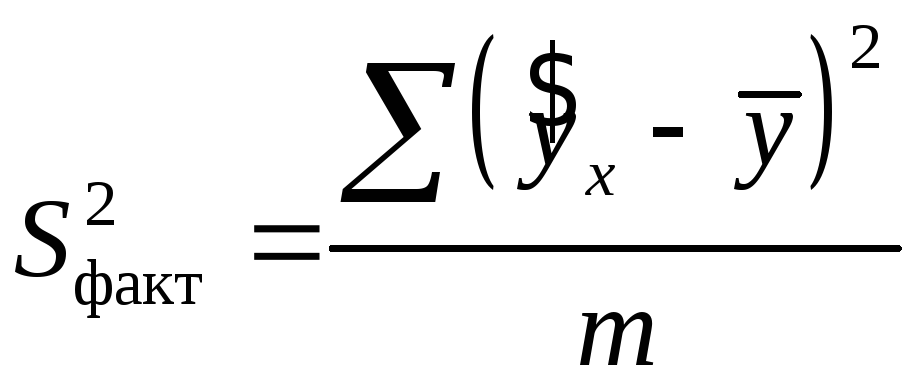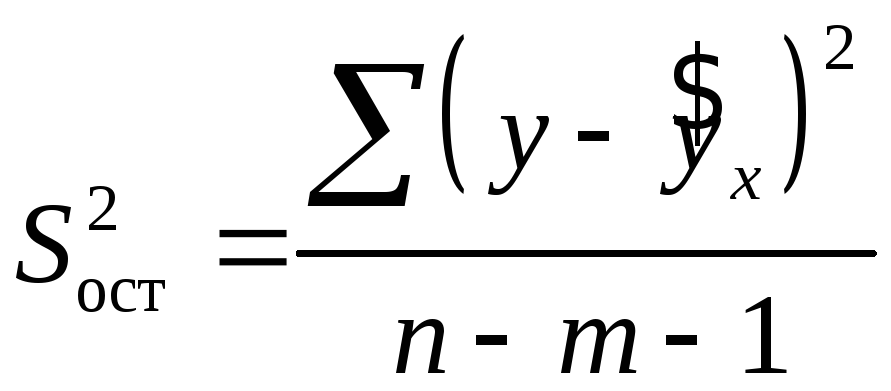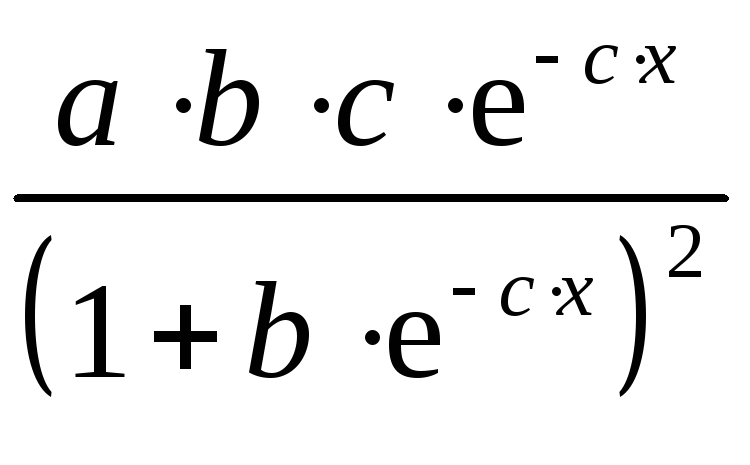- •Розділ 1. Побудова математичної моделі парної і непарної регресії та кореляції наск «Оранта»
- •1.1 Характеристики застосовуваних математичних моделей
- •1.2 Модель парної регресії страхування майна на прикладі наск «Оранта»
- •Розділ 2. Побудова оптимізаційної моделі для формування оптимального портфеля страхових послуг наск «Оранта»
- •Розділ 3. Застосування інформаційних систем і технологій у страховій діяльності
- •3.1. Інформаційні технології в наск «Оранта»
- •4.2. Опис технологій колективної роботи
- •Нові компоненти та можливості ExchangeServer 2013
- •Порівняльна характеристика Microsoft Dynamics crm та Системи страхування
- •Порівняльна характеристика технологій колективної роботи
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ
ВІННИЦЬКИЙ ФІНАНСОВО-ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
Кафедра економічної кібернетики
Звіт
з науково-дослідної роботи кваліфікаційної
практики інформаційно-аналітичних систем економіки
на тему:__________________________________________
________________________________________________________________
студента V курсу денної форми навчання
спеціальності «Економічна кібернетика»
за програмою
«Економічна кібернетика»
_____________________________________________
(прізвище, ім’я, по батькові)
Науковий керівник _________________________
____________________________ (прізвище, ім’я, по батькові)
науковий ступінь, наукове звання
Вінниця - 2014
ЗМІСТ
ВСТУП 3
РОЗДІЛ 1. ПОБУДОВА МАТЕМАТИЧНОЇ МОДЕЛІ ПАРНОЇ І НЕПАРНОЇ РЕГРЕСІЇ ТА КОРЕЛЯЦІЇ НАСК «Оранта» 5
1.1. Характеристики застосовуваних математичних моделей 5
1.2. Модель парної регресії страхування майна на прикладі НАСК «Оранта» 22
РОЗДІЛ 2. ПОБУДОВА ОПТИМІЗАЦІЙНОЇ МОДЕЛІ ДЛЯ ФОРМУВАННЯ ОПТИМАЛЬНОГО ПОРТФЕЛЯ СТРАХОВИХ ПОСЛУГ НАСК «Оранта» 35
РОЗДІЛ 3. ЗАСТОСУВАННЯ ІНФОРМАЦІЙНИХ СИСТЕМ І ТЕХНОЛОГІЙ У БАНКІВСЬКІЙ ДІЯЛЬНОСТІ 43
3.1. Інформаційні технології в НАСК «Оранта» 43
3.2 Опис технологій колективної роботи. 45
ВИСНОВКИ 54
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ 55
Вступ
Страхування – це стратегічний сегмент економіки, оскільки воно дозволяє суттєво знизити навантаження на витратну частину бюджетів різних рівнів; сприяє соціально-економічній стабільності в суспільстві, тому що є важливим елементом соціального захисту населення; дозволяє оптимізувати діяльність суб’єктів економіки за рахунок централізованих фондів фінансових ресурсів; забезпечує компенсацію збитків, завданих юридичним і фізичним особам в результаті настання несприятливих подій; є джерелом внутрішніх довгострокових інвестицій в економіку країни.
Аналіз взаємозв'язків, властивих досліджуваним процесам і явищам, є найважливішою задачею статистичних досліджень. У тих випадках, коли мова йде про явища й процеси, що володіють складною структурою й різноманіттям властивих їм зв'язків, такий аналіз являє собою складну задачу. Насамперед необхідно встановити наявність взаємозв'язків і їх характер. Слідом за цим виникає питання про тісноту взаємозв'язків і ступені впливу різних факторів (причин) на результат, що цікавить дослідника. Якщо риси й властивості досліджуваних об'єктів можуть бути виміряні й виражені кількісно, то аналіз взаємозв'язків може вестися на основі застосування математичних методів.
Використання цих методів дозволяє перевірити гіпотезу про наявність або відсутність взаємозв'язків між тими або іншими ознаками, висунуту на основі змістовного аналізу. Далі, лише за допомогою математичних методів можна встановити тісноту й характер взаємозв'язків або виявити силу (ступінь) впливу різних факторів на результат.
Найбільш розробленими в математичній статистиці методами аналізу взаємозв'язків є кореляційний і регресійний аналіз.
Аналіз статистичного, або кореляційного, зв'язків припускає виявлення форми зв'язків, а також оцінки їх тісноти. Перша задача вирішується методами регресійного аналізу, друга — методами кореляційного аналізу. Регресійний аналіз зводиться до опису статистичного зв'язку за допомогою підходящої функціональної залежності. Кореляційний аналіз дозволяє оцінювати тісноту зв'язку за допомогою спеціальних показників, причому вибір їх залежить від виду функціональної залежності, придатної для адекватного опису розглянутого статистичного взаємозв'язку.
Метою роботи є теоретичне обґрунтування наукових положень та розроблення практичних рекомендацій щодо удосконалення діяльності страхової компанії.
Досягнення поставленої мети зумовило вирішення таких завдань:
дослідити фінансово-економічну необхідність удосконалення управління діяльністю НАСК «Оранта»
визначити способи оцінки стратегій розвитку страхової компанії;
дослідити методи управління діяльністю страхової компанії;
Об’єктом дослідження стала НАСК «Оранта».
Розділ 1. Побудова математичної моделі парної і непарної регресії та кореляції наск «Оранта»
1.1 Характеристики застосовуваних математичних моделей
Парна регресія і кореляція.
Парна
регресія являє собою регресію між двома
змінними –
![]() і
і![]() ,
тобто модель виду:
,
тобто модель виду:
![]() (1)
(1)
де
![]() – залежна змінна (результативна ознака);
– залежна змінна (результативна ознака);
![]() –незалежна,
або пояснююча, змінна ( ознака-фактор).
–незалежна,
або пояснююча, змінна ( ознака-фактор).
Між
змінними
![]() й
й![]() немає строгої функціональної залежності,
тому практично в кожному окремому
випадку величина
немає строгої функціональної залежності,
тому практично в кожному окремому
випадку величина![]() складається із двох доданків:
складається із двох доданків:
![]() (2)
(2)
де
![]() – фактичне значення результативної
ознаки;
– фактичне значення результативної
ознаки;
![]() –теоретичне
значення результативної ознаки, знайдене
виходячи з рівняння регресії;
–теоретичне
значення результативної ознаки, знайдене
виходячи з рівняння регресії;
![]() –випадкова
величина, що характеризує відхилення
реального значення результативної
ознаки від теоретичного, знайденого по
рівнянню регресії.
–випадкова
величина, що характеризує відхилення
реального значення результативної
ознаки від теоретичного, знайденого по
рівнянню регресії.
Випадкова
величина
![]() називається також збурюванням. Вона
включає вплив не врахованих у моделі
факторів, випадкових помилок і особливостей
виміру. Її присутність у моделі породжено
трьома джерелами: специфікацією моделі,
вибірковим характером вихідних даних,
особливостями виміру змінних.
називається також збурюванням. Вона
включає вплив не врахованих у моделі
факторів, випадкових помилок і особливостей
виміру. Її присутність у моделі породжено
трьома джерелами: специфікацією моделі,
вибірковим характером вихідних даних,
особливостями виміру змінних.
Від
правильно обраної специфікації моделі
залежить величина випадкових помилок:
вони тим менше, чим у більшій мері
теоретичні значення результативної
ознаки
![]() ,
підходять фактичним даним
,
підходять фактичним даним![]() .
.
До
помилок специфікації відносять
неправильний вибір тієї або іншої
математичної функції для
![]() й недооблік у рівнянні регресії
якого-небудь істотного фактору, тобто
використання парної регресії замість
множинної.
й недооблік у рівнянні регресії
якого-небудь істотного фактору, тобто
використання парної регресії замість
множинної.
У
парній регресії вибір виду математичної
функції
![]() може бути здійснено трьома методами:
може бути здійснено трьома методами:
графічним;
аналітичним, тобто виходячи з теорії досліджуваного взаємозв'язку;
експериментальним.
При вивченні залежності між двома ознаками графічний метод добору виду рівняння регресії досить наочний. Він заснований на полі кореляції. Основні типи кривих, використовувані при кількісній оцінці зв'язків, представлені на рис. 1
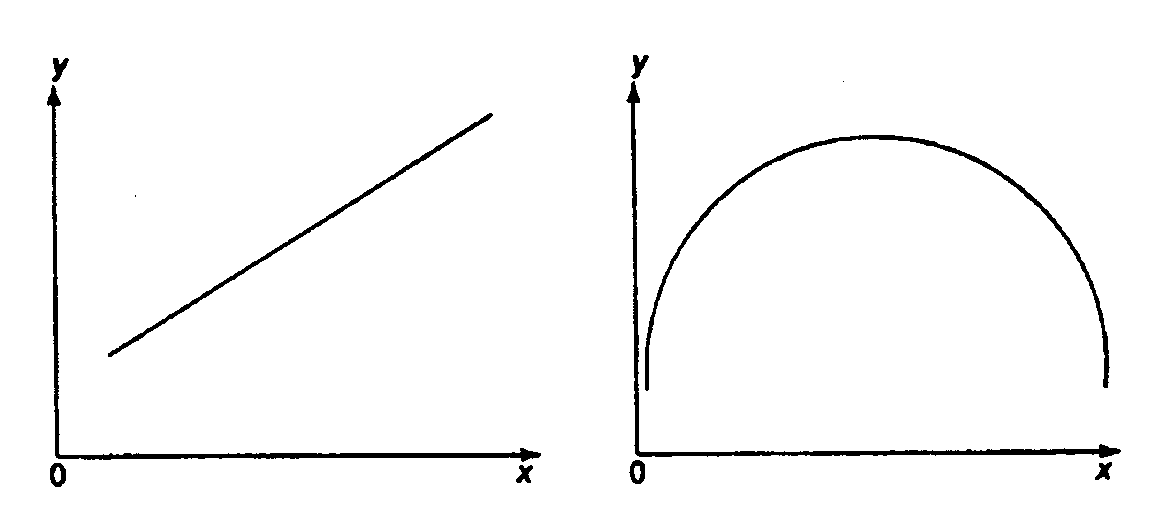
![]()
![]()

![]()
![]()

![]()
![]()
Рис. 1. Основні типи кривих, використовувані при кількісній оцінці зв'язків між двома змінними
Значний інтерес представляє аналітичний метод вибору типу рівняння регресії. Він заснований на вивченні матеріальної природи зв'язки досліджуваних ознак.
При обробці інформації на комп'ютері вибір виду рівняння регресії звичайно здійснюється експериментальним методом.
Якщо
рівняння проходить через усі точки
кореляційного поля, тобто
![]() ,
то залишкова дисперсія дорівнює нулю
(
,
то залишкова дисперсія дорівнює нулю
(![]() ).
).
![]() (3)
(3)
На практиці найчастіше має місце розсіювання точок, тому найкращою визнається модель із найменшою величиною залишкової дисперсії.
Для побудови гарної моделі необхідно, щоб число спостережень в 7-8 раз перевершувало число параметрів моделі, що розраховуються.
Лінійна модель парної регресії
Розглянемо найпростішу модель парної регресії – лінійну регресію. Лінійна регресія знаходить широке застосування в економетриці через чітку економічну інтерпретацію її параметрів.
Лінійна регресія зводиться до знаходження рівняння виду
![]() або
або
![]() . (4)
. (4)
Рівняння
виду
![]() дозволяє за заданими значенням фактору
дозволяє за заданими значенням фактору![]() знаходити теоретичні значення
результативної ознаки, підставляючи в
нього фактичні значення фактору
знаходити теоретичні значення
результативної ознаки, підставляючи в
нього фактичні значення фактору![]() .
.
Побудова
лінійної регресії зводиться до оцінки
її параметрів –
![]() і
і![]() .
Класичний підхід до оцінювання параметрів
лінійної регресії заснований на методі
найменших квадратів (МНК). МНК дозволяє
одержати такі оцінки параметрів
.
Класичний підхід до оцінювання параметрів
лінійної регресії заснований на методі
найменших квадратів (МНК). МНК дозволяє
одержати такі оцінки параметрів![]() і
і![]() ,
при яких сума квадратів відхилень
фактичних значень результативної ознаки
,
при яких сума квадратів відхилень
фактичних значень результативної ознаки![]() від теоретичних
від теоретичних![]() мінімальна:
мінімальна:
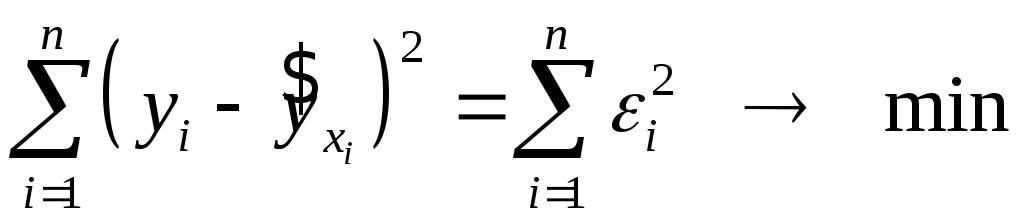 (5)
(5)
Як
відомо з курсу математичного аналізу,
щоб знайти мінімум функції (5), треба
обчислити частки похідні по кожному з
параметрів
![]() і
і![]() й прирівняти їх до нуля. Позначимо
й прирівняти їх до нуля. Позначимо![]() через
через![]() ,
тоді:
,
тоді:
![]() .
.
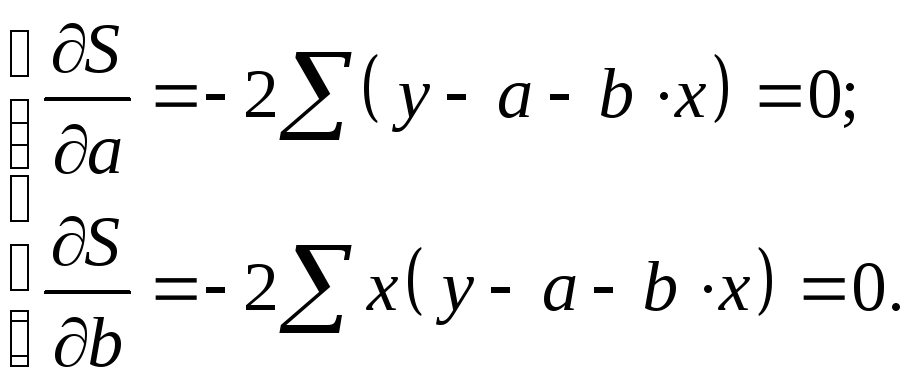 (6)
(6)
Після
нескладних перетворень, одержимо
нормальну систему лінійних рівнянь для
оцінки параметрів
![]() і
і![]() :
:
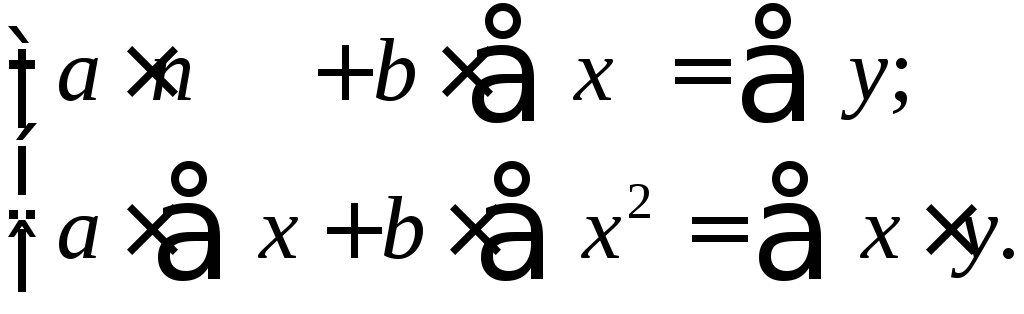 (7)
(7)
Вирішуючи
систему рівнянь (7), знайдемо шукані
оцінки параметрів
![]() і
і![]() .
Можна скористатися наступними готовими
формулами, які випливають безпосередньо
з розв'язку системи (7):
.
Можна скористатися наступними готовими
формулами, які випливають безпосередньо
з розв'язку системи (7):
![]() ,
,![]() (8)
(8)
де![]() ,
,![]() ,
,![]() ,
,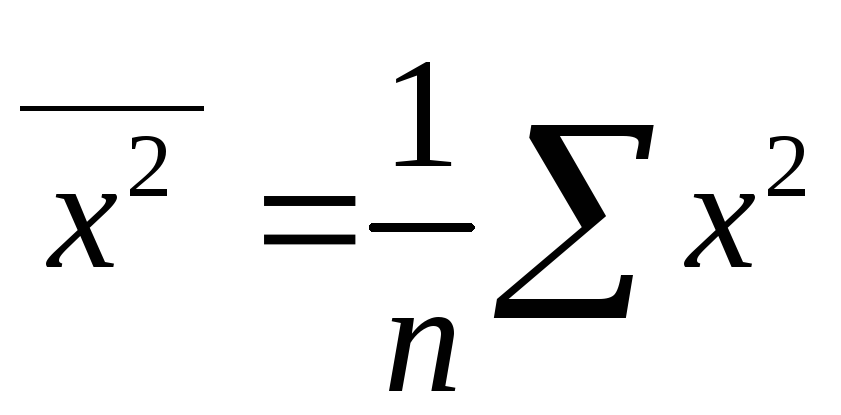 .
.
Параметр
![]() називається коефіцієнтом регресії.
Його величина показує середню зміну
результату зі зміною фактору на одну
одиницю.
називається коефіцієнтом регресії.
Його величина показує середню зміну
результату зі зміною фактору на одну
одиницю.
Можливість чіткої економічної інтерпретації коефіцієнта регресії зробила лінійне рівняння регресії досить розповсюдженим в економетричних дослідженнях.
Формально
![]() – значення
– значення![]() при
при![]() .
Якщо ознака-фактор
.
Якщо ознака-фактор![]() не може мати нульового значення, то
вищевказане трактування вільного члена
не може мати нульового значення, то
вищевказане трактування вільного члена![]() не має змісту, тобто параметр
не має змісту, тобто параметр![]() може не мати економічного змісту.
може не мати економічного змісту.
Рівняння
регресії завжди доповнюється показником
тісноти зв'язки. При використанні
лінійної регресії як такого показника
виступає лінійний коефіцієнт кореляції![]() ,
який можна розрахувати по наступних
формулах:
,
який можна розрахувати по наступних
формулах:
![]() (9)
(9)
де![]() ,
,
![]()
Лінійний
коефіцієнт кореляції перебуває в межах:
![]() .
Чим ближче абсолютне значення
.
Чим ближче абсолютне значення![]() до одиниці, тем сильніше лінійний зв'язок
між факторами ( при
до одиниці, тем сильніше лінійний зв'язок
між факторами ( при![]() маємо строгу функціональну залежність).
Але слід мати на увазі, що близькість
абсолютної величини лінійного коефіцієнта
кореляції до нуля ще не означає відсутності
зв'язку між ознаками. При іншій (нелінійній)
специфікації моделі зв'язок між ознаками
може виявитися досить тісним.
маємо строгу функціональну залежність).
Але слід мати на увазі, що близькість
абсолютної величини лінійного коефіцієнта
кореляції до нуля ще не означає відсутності
зв'язку між ознаками. При іншій (нелінійній)
специфікації моделі зв'язок між ознаками
може виявитися досить тісним.
Для
оцінки якості добору лінійної функції
розраховується квадрат лінійного
коефіцієнта кореляції
![]() ,
називаний коефіцієнтом детермінації.
Коефіцієнт детермінації характеризує
частку дисперсії результативної ознаки
,
називаний коефіцієнтом детермінації.
Коефіцієнт детермінації характеризує
частку дисперсії результативної ознаки![]() ,
що пояснюється регресією, у загальній
дисперсії результативної ознаки:
,
що пояснюється регресією, у загальній
дисперсії результативної ознаки:
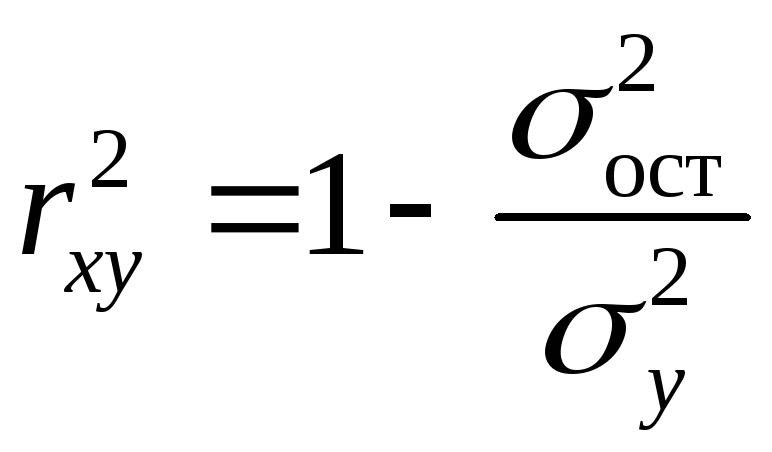 ,
(10)
,
(10)
Де
![]() ,
,![]() .
.
Відповідно
величина
![]() характеризує частку дисперсії
характеризує частку дисперсії
![]() ,
викликану впливом інших, не врахованих
у моделі, факторів.
,
викликану впливом інших, не врахованих
у моделі, факторів.
Після того як знайдено рівняння лінійної регресії, проводиться оцінка значимості як рівняння в цілому, так і окремих його параметрів.
Перевірити значимість рівняння регресії – значить установити, чи відповідає математична модель, що виражає залежність між змінними, експериментальним даним і чи досить включених у рівняння пояснюючих змінних (однієї або декількох) для опису залежної змінної.
Щоб мати загальне судження про якість моделі з відносних відхилень за кожним спостереженням, визначають середню помилку апроксимації:
 . (11)
. (11)
Середня помилка апроксимації не повинна перевищувати 8-10%.
Оцінка
значимості рівняння регресії в цілому
проводиться на основі
![]() -
критерію Фішера, якому передує дисперсійний
аналіз. У математичній статистиці
дисперсійний аналіз розглядається як
самостійний інструмент статистичного
аналізу. В економетриці він застосовується
як допоміжний засіб для вивчення якості
регресійної моделі.
-
критерію Фішера, якому передує дисперсійний
аналіз. У математичній статистиці
дисперсійний аналіз розглядається як
самостійний інструмент статистичного
аналізу. В економетриці він застосовується
як допоміжний засіб для вивчення якості
регресійної моделі.
Згідно
з основною ідеєю дисперсійного аналізу,
загальна сума квадратів відхилень
змінної
![]() від середнього значення
від середнього значення![]() розкладається на дві частини – «пояснену»
і «непояснену»:
розкладається на дві частини – «пояснену»
і «непояснену»:
![]() (12)
(12)
де
![]() – загальна сума квадратів відхилень;
– загальна сума квадратів відхилень;
![]() –сума
квадратів відхилень, пояснена регресією
(або факторна сума квадратів відхилень);
–сума
квадратів відхилень, пояснена регресією
(або факторна сума квадратів відхилень);
![]() –залишкова
сума квадратів відхилень, що характеризує
вплив неврахованих у моделі факторів.
–залишкова
сума квадратів відхилень, що характеризує
вплив неврахованих у моделі факторів.
Схема
дисперсійного аналізу має вигляд,
представлений у таблиці 1 (![]() – число спостережень,
– число спостережень,![]() – число параметрів при змінній
– число параметрів при змінній![]() ).
).
Таблиця 1.3
|
Компоненти дисперсії |
Сума квадратів |
Число ступенів волі |
Дисперсія на один ступінь волі |
|
Загальна |
|
|
|
|
Факторна |
|
|
|
|
Залишкова |
|
|
|
Визначення
дисперсії на один ступінь волі приводить
дисперсії до порівнянного виду.
Зіставляючи факторну й залишкову
дисперсії розраховуючи на один ступінь
волі, одержимо величину
![]() -
критерію Фішера:
-
критерію Фішера:
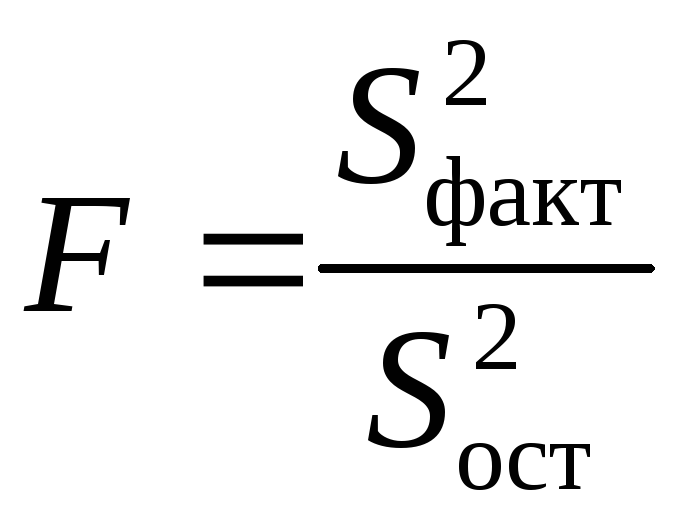 . (13)
. (13)
Фактичне
значення
![]() -критерію
Фішера (20) рівняється з табличним
значенням
-критерію
Фішера (20) рівняється з табличним
значенням![]() при рівні значимості
при рівні значимості![]() й ступенях волі
й ступенях волі![]() й
й![]() .
При цьому, якщо фактичне значення
.
При цьому, якщо фактичне значення![]() -критерію
більше табличного, то визнається
статистична значимість рівняння в
цілому.
-критерію
більше табличного, то визнається
статистична значимість рівняння в
цілому.
Для
парної лінійної регресії![]() ,
тому
,
тому
 . (14)
. (14)
Величина
![]() -
критерію пов'язана з коефіцієнтом
детермінації
-
критерію пов'язана з коефіцієнтом
детермінації![]() ,
і її можна розрахувати по наступній
формулі:
,
і її можна розрахувати по наступній
формулі:
 . (15)
. (15)
У парній лінійній регресії оцінюється значимість не тільки рівняння в цілому, але й окремих його параметрів.
Для оцінки статистичної значимості коефіцієнтів регресії й кореляції розраховуються t-критерій Ст’юдента й довірчі інтервали кожного з показників. Оцінка значимості коефіцієнтів регресії й кореляції за допомогою t-критерію Ст’юдента проводиться шляхом зіставлення їх значень із величиною випадкової помилки:
![]()
![]()
![]()
Випадкові помилки параметрів лінійної регресії й коефіцієнта кореляції визначаються за формулами:
 (16)
(16)
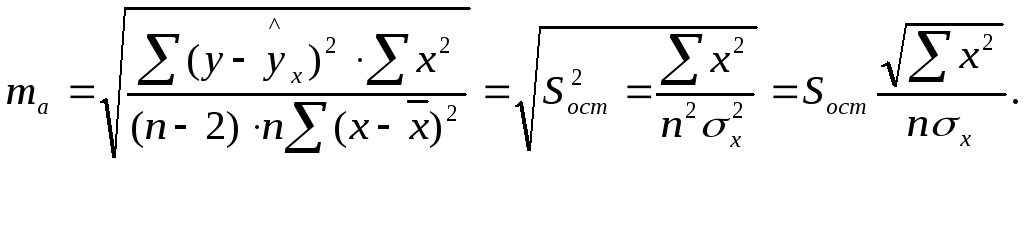 (17)
(17)
![]() (18)
(18)
Величина
стандартної помилки разом з
![]() -розподілом
Ст’юдента при
-розподілом
Ст’юдента при![]() ступенях волі застосовується для
перевірки істотності коефіцієнта
регресії й для розрахунків його довірчого
інтервалу.
ступенях волі застосовується для
перевірки істотності коефіцієнта
регресії й для розрахунків його довірчого
інтервалу.
Для
оцінки істотності коефіцієнта регресії
визначається фактичне значення
![]() -критерію
Ст’юдента, яке потім рівняється з
табличним значенням при певному рівні
значимості
-критерію
Ст’юдента, яке потім рівняється з
табличним значенням при певному рівні
значимості![]() й числі ступенів волі
й числі ступенів волі![]() .
.
Якщо tтабл tфак, то a, b і rху не випадково відрізняються від нуля й сформувалися під впливом систематично діючого фактору x. Якщо tтабл tфак, то визнається випадкова природа формування a, b або rху.
Існує
зв'язок між
![]() -критерієм
Ст’юдента й
-критерієм
Ст’юдента й![]() -критерієм
Фішера:
-критерієм
Фішера:
![]() . (19)
. (19)
Для розрахунків довірчого інтервалу визначаємо граничну помилку для кожного показника
![]()
![]()
Формули для розрахунків довірчих інтервалів мають такий вигляд:
![]()
![]()
![]()
![]()
![]()
![]()
Якщо в границі довірчого інтервалу попадає нуль, тобто нижня границя негативна, а верхня позитивна, то оцінюваний параметр ухвалюється нульовим, тому що він не може одночасно ухвалювати й позитивне, і негативне значення.
У
прогнозних розрахунках по рівнянню
регресії визначається
![]() значення, що передбачається, як точковий
прогноз
значення, що передбачається, як точковий
прогноз![]() при
при![]() ,
тобто шляхом підстановки в рівняння
регресії
,
тобто шляхом підстановки в рівняння
регресії![]() відповідного значення
відповідного значення![]() .
Однак точковий прогноз явно не реальний.
Тому він доповнюється розрахунками
стандартної помилки
.
Однак точковий прогноз явно не реальний.
Тому він доповнюється розрахунками
стандартної помилки![]() ,
тобто
,
тобто![]() ,
і відповідно інтервальною оцінкою
прогнозного значення
,
і відповідно інтервальною оцінкою
прогнозного значення![]() :
:
![]() ,
,
де![]() ,
а
,
а![]() – середня помилка прогнозованого
індивідуального значення:
– середня помилка прогнозованого
індивідуального значення:
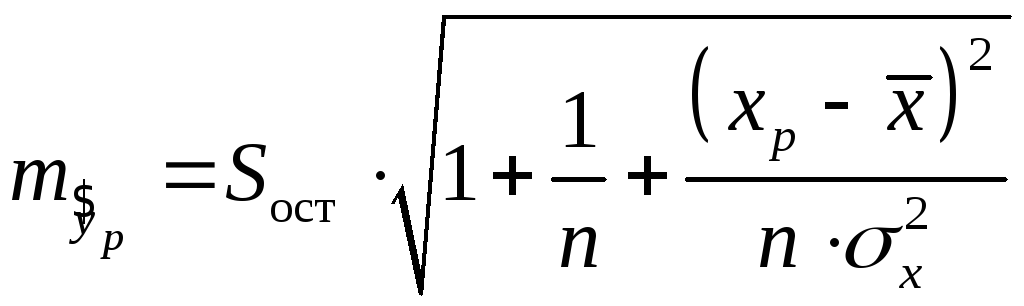 (20)
(20)
Нелінійні моделі парної регресії
Якщо між економічними явищами існують нелінійні співвідношення, то вони виражаються за допомогою відповідних нелінійних функцій.
Розрізняють два класи нелінійних регресій:
Регресії, нелінійні щодо включених в аналіз пояснюючих змінних, але лінійні по оцінюваних параметрах, наприклад
– поліноми
різних ступенів –![]() ,
,![]() ;
;
– рівностороння
гіпербола –
![]() ;
;
– напівлогарифмічна
функція –
![]() .
.
Регресії, нелінійні по оцінюваних параметрах, наприклад
– степенева
–
![]() ;
;
– показова
–
![]() ;
;
– експонентна
–
![]() .
.
Регресії нелінійні по включених змінних приводяться до лінійного виду простою заміною змінних, а подальша оцінка параметрів проводиться за допомогою методу найменших квадратів. Розглянемо деякі функції.
Парабола
другого ступеня
![]() приводиться до лінійного виду за
допомогою заміни:
приводиться до лінійного виду за
допомогою заміни:![]() .
У результаті приходимо до двофакторного
рівняння
.
У результаті приходимо до двофакторного
рівняння![]() ,
оцінка параметрів якого за допомогою
МНК приводить до системи наступних
нормальних рівнянь:
,
оцінка параметрів якого за допомогою
МНК приводить до системи наступних
нормальних рівнянь:
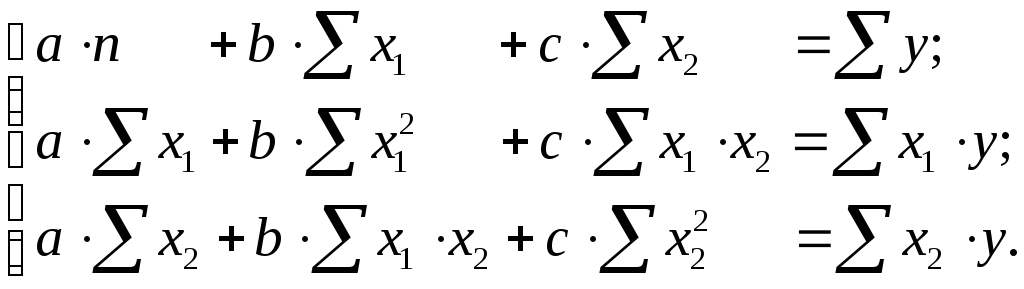
А після зворотної заміни змінних одержимо
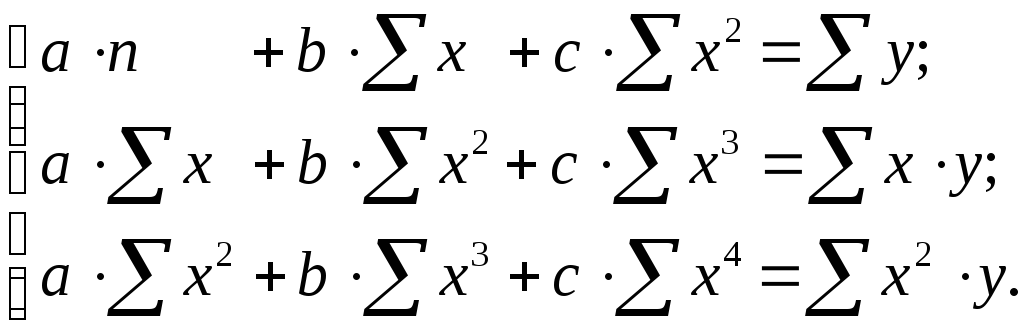 (21)
(21)
Парабола другого ступеня звичайно застосовується у випадках, коли для певного інтервалу значень фактору міняється характер зв'язку розглянутих ознак: прямий зв'язок міняється на зворотній або зворотній на прямий.
Рівностороння
гіпербола
![]() може бути використана для характеристики
зв'язку питомих витрат сировини,
матеріалів, палива від об'єму продукції,
що випускається, часу обігу товарів від
величини товарообігу, відсотка приросту
заробітної плати від рівня безробіття
(наприклад, крива А.В. Філліпса), витрат
на непродовольчі товари від доходів
або загальної суми витрат (наприклад,
криві Є. Енгеля) і в інших випадках.
Гіпербола приводиться до лінійного
рівняння простою заміною:
може бути використана для характеристики
зв'язку питомих витрат сировини,
матеріалів, палива від об'єму продукції,
що випускається, часу обігу товарів від
величини товарообігу, відсотка приросту
заробітної плати від рівня безробіття
(наприклад, крива А.В. Філліпса), витрат
на непродовольчі товари від доходів
або загальної суми витрат (наприклад,
криві Є. Енгеля) і в інших випадках.
Гіпербола приводиться до лінійного
рівняння простою заміною:![]() .
Система лінійних рівнянь при застосуванні
МНК буде виглядати в такий спосіб:
.
Система лінійних рівнянь при застосуванні
МНК буде виглядати в такий спосіб:
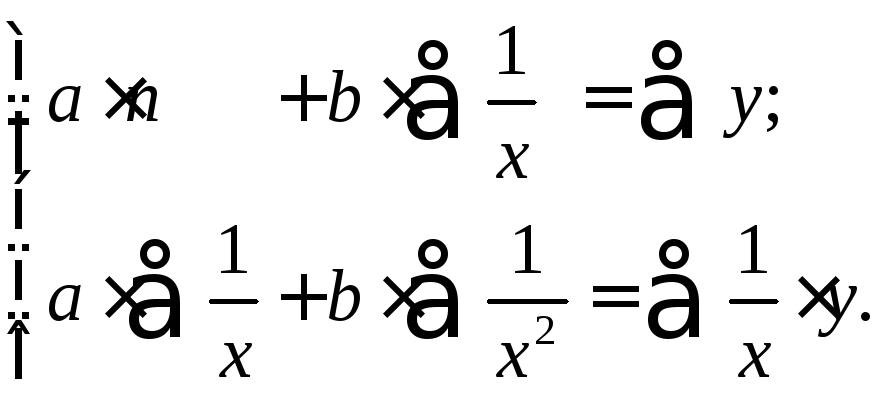 (22)
(22)
Аналогічним
образом приводяться до лінійного виду
залежності![]() ,
,![]() і інші.
і інші.
Трохи інакше йде справа з регресіями нелінійними по оцінюваних параметрах, які діляться на два типи: нелінійні моделі внутрішньо лінійні (приводяться до лінійного виду за допомогою відповідних перетворень, наприклад, логарифмуванням) і нелінійні моделі внутрішньо нелінійні ( до лінійного виду не приводяться).
До
внутрішньо лінійних моделей відносять,
наприклад, степеневу функцію –![]() ,
показову –
,
показову –![]() ,
експонентну –
,
експонентну –![]() ,
логістичну –
,
логістичну –![]() ,
зворотну –
,
зворотну –![]() .
.
До внутрішньо нелінійних моделей можна, наприклад, віднести наступні моделі
![]() ,
,
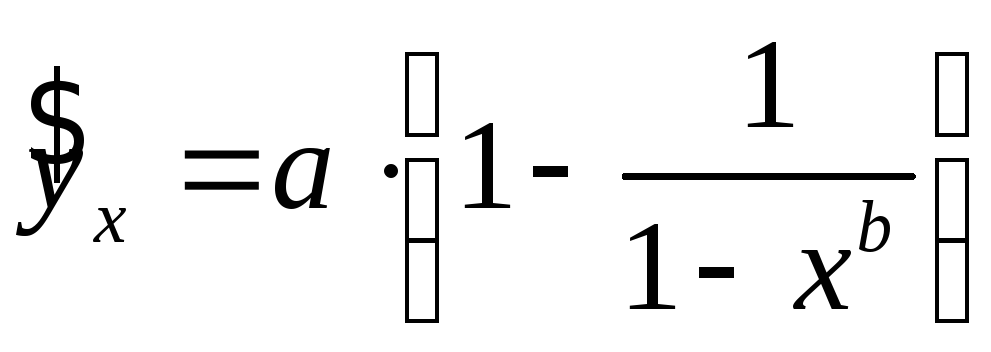
Серед
нелінійних моделей найбільше часто
використовується степенева функція
![]() ,
яка приводиться до лінійного виду
логарифмуванням:
,
яка приводиться до лінійного виду
логарифмуванням:
![]() ;
;
![]() ;
;
![]() ,
,
де
![]() .
Тобто МНК ми застосовуємо для перетворених
даних:
.
Тобто МНК ми застосовуємо для перетворених
даних:

а потім потенцірованням знаходимо шукане рівняння.
Широке
використання степеневої функції
пов'язане з тим, що параметр
![]() у ній має чітке економічне тлумачення
– вінє
коефіцієнтом еластичності. Коефіцієнт
еластичності показує, на скільки
відсотків змінитися в середньому
результат, якщо фактор зміниться на 1%.
Формула для розрахунків коефіцієнта
еластичності має вигляд:
у ній має чітке економічне тлумачення
– вінє
коефіцієнтом еластичності. Коефіцієнт
еластичності показує, на скільки
відсотків змінитися в середньому
результат, якщо фактор зміниться на 1%.
Формула для розрахунків коефіцієнта
еластичності має вигляд:
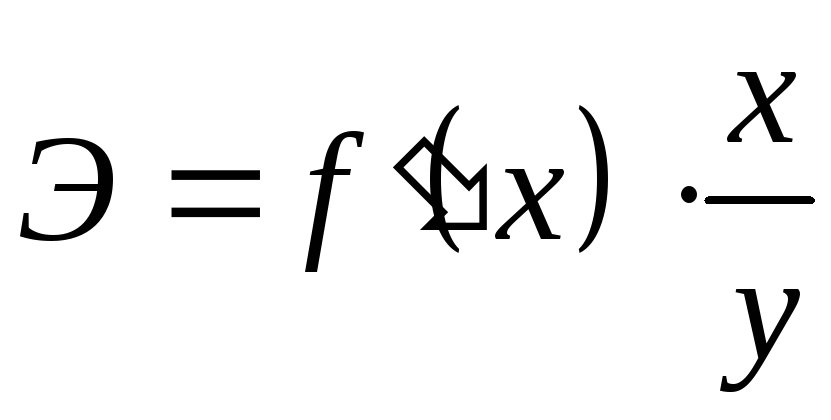 .
(23)
.
(23)
Тому
що для інших функцій коефіцієнт
еластичності не є постійною величиною,
а залежить від відповідного значення
фактору
![]() ,
то зазвичай розраховується середній
коефіцієнт еластичності:
,
то зазвичай розраховується середній
коефіцієнт еластичності:
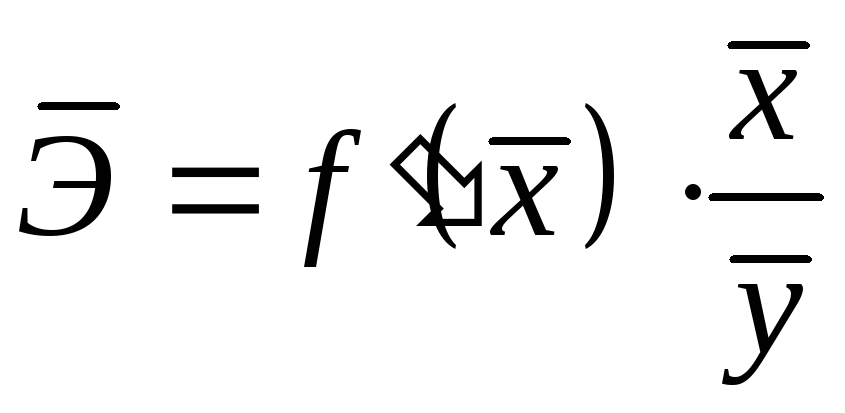 .
(24)
.
(24)
Приведемо формули для розрахунків середніх коефіцієнтів еластичності для найбільше часто використовуваних типів рівнянь регресії:
Таблиця 1.4
|
Вид
функції,
|
Перша
похідна,
|
Середній
коефіцієнт еластичності,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продовження таблиці 1.4
|
|
|
|
|
|
|
|
|
|
|
|
Можливі випадки, коли розрахунок коефіцієнта еластичності не має змісту. Це відбувається тоді, коли для розглянутих ознак безглузде визначення зміни у відсотках.
Рівняння нелінійної регресії, так само, як і у випадку лінійної залежності, доповнюється показником тісноти зв'язки. У цьому випадку це індекс кореляції:
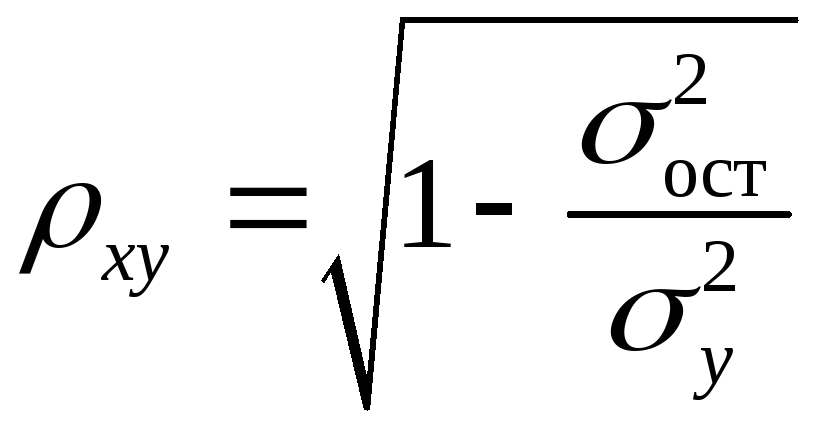 ,
(25)
,
(25)
де
![]() – загальна дисперсія результативної
ознаки
– загальна дисперсія результативної
ознаки![]() ,
,
![]() –залишкова
дисперсія.
–залишкова
дисперсія.
Величина
даного показника перебуває в межах:
![]() .
Чим ближче значення індексу кореляції
до одиниці, тем тісніше зв'язок розглянутих
ознак, тим більше надійне рівняння
регресії.
.
Чим ближче значення індексу кореляції
до одиниці, тем тісніше зв'язок розглянутих
ознак, тим більше надійне рівняння
регресії.
Квадрат
індексу кореляції називається індекс
детермінації й характеризує частку
дисперсії результативної ознаки
![]() ,
що пояснюється регресією, у загальній
дисперсії результативної ознаки:
,
що пояснюється регресією, у загальній
дисперсії результативної ознаки:
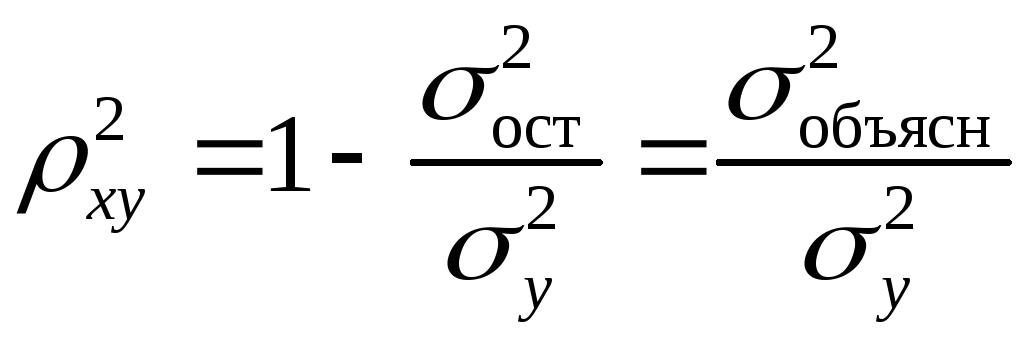 , (26)
, (26)
тобто має той же зміст, що й у лінійній регресії;
![]()
Індекс
детермінації
![]() можна порівнювати з коефіцієнтом
детермінації
можна порівнювати з коефіцієнтом
детермінації![]() для обґрунтування можливості застосування
лінійної функції. Чим більше кривизна
лінії регресії, тим величина
для обґрунтування можливості застосування
лінійної функції. Чим більше кривизна
лінії регресії, тим величина![]() менше
менше![]() .
А близькість цих показників указує на
те, що немає необхідності ускладнювати
форму рівняння регресії й можна
використовувати лінійну функцію.
.
А близькість цих показників указує на
те, що немає необхідності ускладнювати
форму рівняння регресії й можна
використовувати лінійну функцію.
Індекс
детермінації використовується для
перевірки істотності в цілому рівняння
регресії по
![]() -критерію
Фішера:
-критерію
Фішера:
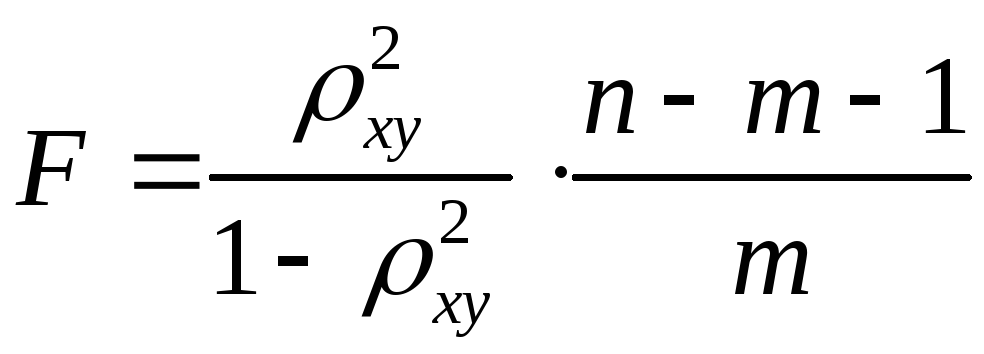 , (27)
, (27)
де
![]() – індекс детермінації,
– індекс детермінації,
![]() –число
спостережень,
–число
спостережень,
![]() –число
параметрів при змінній
–число
параметрів при змінній
![]() .
.
Фактичне
значення
![]() -критерію
(35) рівняється з табличним при рівні
значимості
-критерію
(35) рівняється з табличним при рівні
значимості![]() й числі ступенів волі
й числі ступенів волі![]() ( для залишкової суми квадратів) і
( для залишкової суми квадратів) і![]() ( для факторної суми квадратів).
( для факторної суми квадратів).