1. Первинна обробка вибірок

1.1 Розглянемо вибірку . Вирішимо питання, чи доцільно складати варіаційний ряд. Із цією метою знайдемо мінімальні та максимальні елементи вибірки. Маємо: . Розмах вибірки - досить малий, тому що обсяг її - , тобто, враховуючи, що елементи вибірки – цілі числа, це означає, що різних можливих варіант у вибірці не більше за . Обсяг вибірки , і це означає, що в середньому на кожну варіанту припадає елемент вибірки. Можна зробити висновок, що в цьому випадку слід працювати з вихідною вибіркою і не складати варіаційний ряд. Але, оскільки цього вимагають умови задачі ,а також тому, що, ймовірно, прибуток по фірмі, а значить і по магазинах, нормально розподілена випадкова величина, зосереджена навколо математичного сподівання, то різних варіант, що зустрічаються для вибірки навколо кінців проміжку , може бути значно менше, ніж можливих значень. Тому будуємо дискретний варіаційний ряд. Коли всі значення вибірки (варіанти – множина різних значень вибірки, впорядкованих за зростанням) були виписані, то виявилося, що їх лише , тобто значно менше за , отже, у подальших формулах за приймаємо ( для дискретного ряду – це кількість різних варіант у вибірці).

1.3 Заповнимо у таблиці 1 стовпчик упорядкованих варіант , стовпчику частот (перевірка: сума за цим стовпчиком дає обсяг вибірки - ) , накопичених частот (сума усіх перших частот до ), відносних частот (сума за стовпчику 1, як сума емпіричних ймовірностей), накопичених відносних частот , де .

1.4 Побудуємо полігон відносних частот варіаційного ряду, скориставшись стовпчиком , . Із цією метою на площині сукупність точок з’єднуємо ламаною лінією (рисунок 1).

1.5 побудуємо емпіричну функцію розподілу вибірки (рисунок 2), скориставшись стовпчиком .

Емпірична функція розподілу для дискретного варіаційного ряду визначається наступним чином:

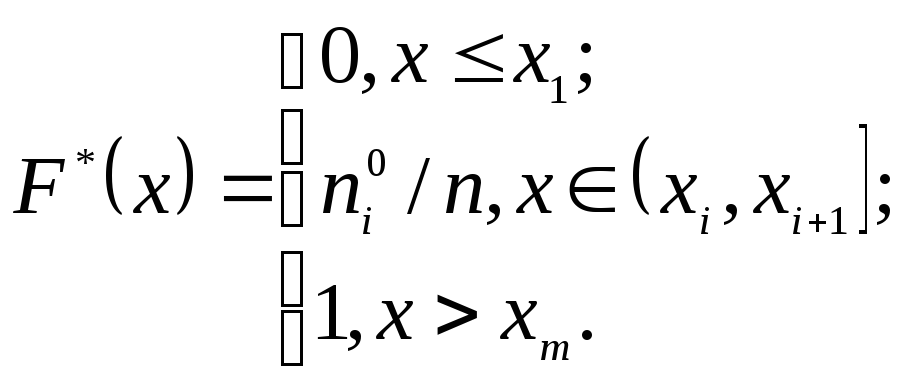
У нашому випадку набуває вигляду:

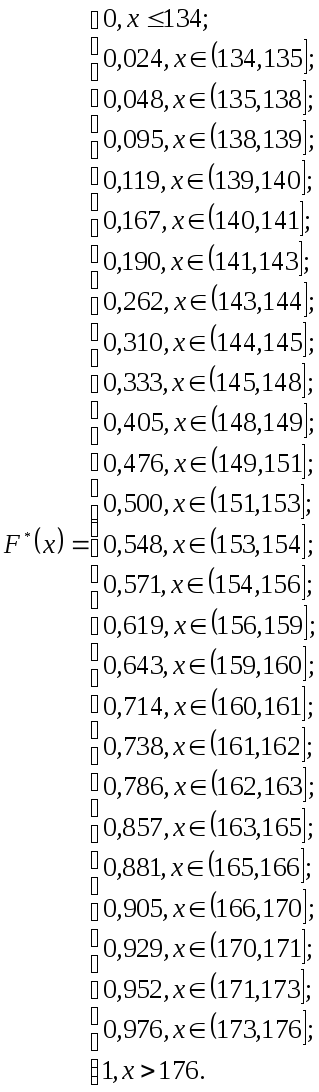
1.1 , 1.1 , 1.3 , 1.3 Аналогічні дії робимо при складанні варіаційних рядів та визначенні відносних і накопичених частот за вибірками . Результати їх зведені у таблицях 2,3.

1.2 Розглянемо вибірку . Вирішимо питання про доцільність складання варіаційного ряду, в тому числі інтервального. З цією метою знайдемо мінімальний ті максимальний елементи вибірки: . Розмах вибірки не дуже малий, тобто, враховуючи, що елементи вибірки – цілі числа, це означає, що різних можливих варіант у вибірці не більше за . Обсяг вибірки . Це означає, що в середньому на кожну варіанту припадає елементи вибірки. Можна зробити висновок, що в цьому випадку має сенс будувати варіаційний ряд. Якщо будувати дискретний ряд, то він буде досить великим, тому скористаємось запропонованою довжиною інтервалу , що дасть можливість обмежити кількість інтервалів числом, близьким до .

Виберемо початок першого інтервалу, його треба вибрати так, щоб перша і остання варіанти не припадали на початок і кінець останнього інтервалу відповідно. Бажано також визначати за формулою: , тобто так, щоб мінімальний елемент вибірки був розташований посередині першого інтервалу. Перевіримо: дійсно є серединою .

Заповнимо шкалу інтервалів, враховуючи, що елемент вибірки, який попадає на правий кінець інтервалу, враховується не у цьому, а в наступному напівінтервалі. Виявляється, що максимальний елемент , тобто попадає в -ий інтервал. Отже, визначили, щ кількість інтервалів у нашому ряді - . Але при заповненні стовпчика частот (таблиця 4) виявляється, що у другий інтервал не попадає жодного елемента вибірки, тому у таблицю цей інтервал не заносимо і у формулах підставляємо .

У тих же формулах для інтервального ряду параметр - довжина інтервалу, отже, .

1.3 Заповнимо у таблиці 4 стовпчик інтервалів, стовпчики частот (перевіряємо, щоб сума за цим стовпчиком була ), накопичених частот , відносних частот (перевіряємо, щоб сума за стовпчиком була ) , накопичених відносних частот , де .

1.4 Для дискретного варіаційного ряду ми будували полігон частот. Для інтервального ряду, з метою одержання візуального уявлення про вигляд графіка щільності розподілу неперервної випадкової величини, побудуємо гістограму. Для цього по осі абсцис відкладемо інтервали і на них, як на основах, побудуємо прямокутники з висотами . Площа обмеженої ступінчатої фігури дорівнює . Для уявлення про вигляд графіка щільності розподілу з’єднуємо плавною кривою середини верхніх основ цих прямокутників (рисунок 3) (площа під цією кривою наближена до ).

1.5 Побудуємо емпіричну функцію розподілу генеральної скпності, представленої вибіркою (рисунок 4), для цього по осі абсцис відкладемо інтервали. Враховуючи те, що накопичена відносна частота - сума всіх перших відносних частот до -го інтервалу включно, на площині побудуємо множину точок і з’єднаємо ці точки плавною кривою, яка і являє собою графік емпіричної функції розподілу неперервно варійованої випадкової величини. Заповнимо решту стовпчиків таблиці 4. заповнимо стовпчик - варіант, якими ми замінюємо всі елементи вибірки, що попадають у -ий інтервал і які є серединами цих інтервалів. Отже,

, .

Тепер в подальшому ми вже вважаємо, що наш ряд дискретний із множиною варіант і їх частотами .