Конспект лекций АиГ_ Реутова ИН_ Часть 1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Приазовский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Отсюда: 2 m 3 2m,

.pdf

Скачиваний:

Добавлен:

05.03.2016

Размер:

4.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 139 10 11 12 13 > Следующая >>>

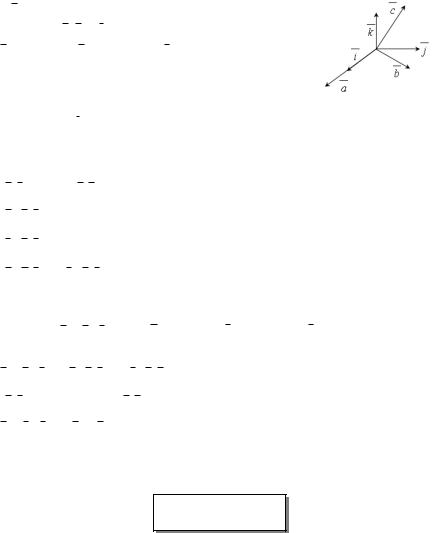
и j были компланарны (рис. 12.6). В этой системе координат a, b и c имеют следующие координаты: a xa ; 0; 0 , b xb ; yb ; 0 и c xc ; yc ; zc .

Согласно

(12.6)

yb zc ; xb zc ; xb yc

xc yb . Тогда

Рис. 12.6

0; xa xb yc xa xc yb ; xa xb zc .

yb zc

xb zc

xb yc xc yb

a, c xa xc , a,b xa xb .

b, a, c xa xc xb ; yb ; 0 xa xb xc ; xa yb xc ; 0 ,

c, a,b xa xb xc ; yc ; zc xa xb xc ; xa xb yc ; xa xb zc .

b, a, c c, a, b 0; xa xb yc xa xc yb ; xa xb zc . Теорема доказана .

Таким образом, формула (12.11) позволяет вычислить двойное векторное произведение значительно быстрее, чем по определению.

N. Найти a b c , если a 2; 3;1 , b 3;1; 2 и c 1; 2;3 .

Решение.

ab c b, a, c c, a,b .

a, c 2 6 3 1, a, b 6 3 2 7.

ab c b 7c 3;1; 2 7;14; 21 10;13;19 .

Ответ. 10;13;19 .

ЛЕКЦИЯ 13.

ПОНЯТИЕ ОБ УРАВНЕНИИ ЛИНИИ. ПРЯМАЯ НА ПЛОСКОСТИ.

Понятие об уравнении линии

Def. Уравнением линии на плоскости в декартовой системе координат

называют уравнение:
F (x, y) 0 ,	(13.1)

которому удовлетворяют координаты (x, y) любой точки этой линии и не удовлетворяют координаты ни одной точки, которые не принадлежат ей.


	N. Например,		x y 0 – уравнение прямой,		проходящей через начало

координат и являющейся биссектрисой І и ІІІ координатных четвертей.
x2 ( y 1)2		25	-	уравнение окружности с центром		в точке O(0;1) и
радиусом R 5.
	Пусть линия L1			задана уравнением F (x, y) 0 , а линия L2			- уравнением
(x, y) 0 .		Точки		пересечения этих линий,	если	они	существуют,

принадлежат обеим линиям, т.е. удовлетворяют обоим уравнениям. Таким

образом, решение задачи по отысканию точек пересечения							L1	и L2	сводится
к решению системы уравнений:
				F (x, y) 0,					(13.2)
									(13.2)
				(x, y) 0.
N. Найти		точки пересечения		окружности	(x 1)2 ( y 3)2			4	и прямой

x y 0.
Решение.
	Решим систему уравнений			(x 1)2 ( y 3)2 4,		Исключая из первого
	Решим систему уравнений					Исключая из первого
				x y 0.
уравнения		y,	получаем:	x2 4x 3 0.	Отсюда		x	1, x 3 и,
							1		2
соответственно,			y1 1, y2 3 . Таким образом, точки (1;1), (3;3)					– искомые.

Def. Алгебраической линией называется такая линия, которая задается в ДСК уравнением F (x, y) 0 , где F (x, y) – многочлен. Степень этого многочлена

называется порядком этой линии.

Def. Линии, которые не являются алгебраическими называются

трансцендентными.

N. x2 3xy 4x 2 y 5 y2 1 0 - алгебраическая линия второго порядка. 5xy x 2 0, y tgx 0, y ln x – трансцендентные линии.

Пусть заданы две функции одного аргумента:

x x(t),	(13.3)
	(13.3)
y y(t).

Условимся рассматривать x и y как координаты некоторой точки M в

заданной системе координат. Тогда при изменении параметра t положение точки M меняется и она перемещается по плоскости. Равенства (13.3)

называются параметрическими уравнениями траектории точки.

Пусть уравнение (13.1) является следствием (13.3), тогда ему удовлетворяют

координаты x x(t),	y y(t)	любой точки M линии (13.3) при	любых t .
Если при этом, если	точка	M пробегает всю линию (13.1), то	уравнение

F (x, y) 0 представляет собой обычное уравнение линии (13.3). Составление такого следствия F (x, y) 0 называют исключением параметра.

N. Исключить параметр из параметрических уравнений траектории точки

x cos t,y sin t.

Решение.

Возведем каждое из уравнений в квадрат и сложим их почленно. Получим: x2 y2 1 .

Значит, точка M движется по окружности с центром в начале координат и радиуса 1. Причем, т.к. t R, то луч OM , образующий с осью Ox угол t,

занимает всевозможные положения. Значит, точка М пробегает указанную окружность бесконечное число раз.

Замечание. Не всегда возможно исключить параметр из параметрических уравнений линии.

Уравнение прямой на плоскости

Th. 13.1

Любая

прямая

на координатной плоскости может быть

задана уравнением первой степени:

ax by c 0

(a2 b2 0).

(13.4)

И, наоборот, любое уравнение первой степени определяет на

плоскости прямую.

Доказательство.

Положение

прямой

однозначно

определяется

точкой

M 0 (x0 ; y0 ),

которая

принадлежит прямой, и вектором n(a;b) l. Будем

называть этот вектор нормальным вектором

, то (a2 b2 0).

Рис. 13.1

прямой или нормалью. Т.к

Выберем M (x; y)

- текущую точку прямой l.

Очевидно,

что M (x; y) l

тогда

и только тогда, когда

M 0 M n или

M 0 M n 0. В координатной форме последнее равенство имеет вид:

a(x x0 ) b( y y0 ) 0.	(13.5)
После раскрытия скобок получаем ax by c 0 , где	c ax0 by0 . Таким
образом, первая часть утверждения теоремы доказана.

2) Пусть (x0 , y0 ) – одно из решений уравнения (13.4), т.е.

ax0 by0 c 0.

(13.6)

Вычтем

из

уравнения

(13.4)

уравнение

(13.6),

получим

a(x x0 ) b( y y0 ) 0. Это

уравнение

является

координатной

записью

условия M 0 M n 0,

где

n(a;b) 0, M 0 (x0 ; y0 ),

M (x; y). Но это условие

определяет прямую, которая проходит через точку М перпендикулярно вектору n . Таким образом, доказано и второе утверждение теоремы .

Замечания.

1. Уравнение a(x x0 ) b( y y0 ) 0 называется уравнением прямой,

проходящей через точку M 0 (x0 ; y0 ) перпендикулярно вектору n(a;b) 0.

2.Уравнение (13.4) называют общим уравнением прямой. Коэффициенты перед переменными в общем уравнении прямой на плоскости имеют вполне определенный геометрический смысл: они являются координатами нормального вектора прямой.

3.Очевидно, что если в уравнении (13.4) c 0, то прямая проходит через начало координат.

4.Если в уравнении (13.4) a 0, то n(0;b) Oy. В этом случае прямая параллельна оси Ox. Аналогично, если в уравнении (13.4) b 0, то прямая параллельна оси Oy.

Уравнение прямой с угловым коэффициентом

Если в

уравнении (13.4)

b 0,

то

его можно переписать в

виде y

. Или, обозначая

l, в виде:

y kx l

(13.7)

Выясним геометрический смысл коэффициентов в уравнении (13.7).

Def. Углом наклона данной прямой к оси Ox называется угол (0 ),

на который следует повернуть против хода часовой стрелки ось Ox до ее совмещения с данной прямой (рис. 13.2, 13.3).

Если прямая параллельна оси Ox, то угол наклона этой прямой к оси Ox принимается равным нулю.

Пусть A1 (x1 , y1 ) и A2 (x2 , y2 ) - две точки (рис. 13.4) на прямой y kx l. Тогда из A1CA2 имеем:


	A2C y2 y1				(kx2 l) (kx1 l)		k(x2 x1 )
tg									k.	(13.8)
	A C		x x		x x		x x
	1	2		1	2	1	2	1

Таким образом, коэффициент k в уравнении прямой равен тангенсу угла наклона прямой к оси Ox и называется угловым коэффициентом прямой. В связи с этим, уравнение (13.7) называется уравнением прямой с угловым коэффициентом.

Рис. 13.2

Рис. 13.3

Рис. 13.4

Очевидно, что ось Oy прямая, заданная уравнением (13.7), пересекает в

точке

A(0; b). Поэтому параметр

уравнении

прямой

угловым

коэффициентом равен ординате точки пересечения прямой с осью Oy.

Другие виды уравнения прямой на плоскости

Положение прямой

l однозначно определяется точкой M 0 (x0 ; y0 ) l и

вектором

m; p

l ,

который

называется направляющим

вектором

прямой l.

Пусть r0 – радиус-вектор точки M 0 , а r

– радиус-вектор текущей

точки

прямой

(рис. 13.5).

M l

тогда

только

тогда, когда

r r 0

M 0 M

s , т.е.

r r0 t s

(t R)

или:

r r0 t s

(t R)

(13.9)

Уравнение (13.9) называется векторным уравнением прямой на плоскости.

В координатной форме уравнение (13.9) записывается в виде:

x x0	mt,
	(t R).
y y0	pt

Уравнения (13.10) называют параметрическими уравнениями

на плоскости.

Условие M 0 M s можно записать в координатной форме:

x x0 y y0 m p

(13.10)

прямой

(13.11)

или

x x0

y y0

(13.12)

Уравнения

(13.11)

(13.12)

удобно

использовать,

если известна точка на

прямой

M 0 (x0 ; y0 )

направляющий

вектор

прямой

m; p .

Уравнение(13.11)

называют

еще

каноническим уравнением прямой.
N. Составьте уравнение прямой, проходящей через
точку A(1; 2) а) параллельно прямой a : 3x y 1 0;				Рис. 13.5
б) перпендикулярно прямой a : 3x y 1 0.
Решение.
а)		3; 1 a,	т.к. искомая прямая параллельна прямой a,	то			3; 1 ее
	n				n
нормальный вектор. На основании формулы (13.5) получаем:
			3(x 1) 1( y 2) 0.
		Или после упрощения: 3x y 5 0.
б)	Т.к. искомая		прямая перпендикулярна прямой a,	то			3; 1 -
						n

направляющий вектор искомой прямой. На основании формулы(13.11) имеем:

	x 1	y 2	;	1(x 1) 3( y 2);	x 3y 5 0.
	3	1

Ответ: а) 3x y 5 0; б)				x 3y 5 0.

Прямая l также однозначно определяется двумя точками M1 (x1 ; y1 ) и M 2 (x2 ; y2 ) (рис. 13.6). В этом случае в качестве направляющего вектора можно

x1 ; y2

y1 .

взять вектор M1M 2

Тогда

уравнения (13.11)

(13.12)

принимают

соответственно вид:

x x1

y y1

x x1

y y1

Рис. 13.6

(13.13)

(13.14)

Взаимное расположение прямых на плоскости

Пусть на координатной плоскости заданы две прямые l1 : a1 x b1 y c1 0 и l2 : a2 x b2 y c2 0. Исследуем их взаимное расположение на плоскости.

Две прямые на плоскости могут либо пересекаться (имеют единственную общую точку), либо параллельны (не имеют общих точек), либо совпадать (имеют бесконечное множество общих точек). Для нахождения точек пересечения прямых составим и исследуем СЛУ:

a1 x b1 y c1 0,a2 x b2 y c2 0.

l1 l2 СЛУ (13.15) имеет единственное решение

a1 b1 . a2 b2

СЛУ

не

имеет

решений

l1 l2

СЛУ

имеет

бесконечно

много

решений

(13.15)

a1	b1	0
a2	b2

b1	0 или
b2

a1 b1 a2 b2

Взаимное расположение прямых на плоскости характеризуется также углом между прямыми. Он однозначно определяется углом между

нормальными векторами этих прямых n1 a1 ;b1 и n2 a2 ;b2 , который обозначим через . Тогда:


cos		n1	n2			a1a2	b1b2		.	(13.16)
cos									.	(13.16)
	n			n	a2	b2	a2	b2
	1			2	1	1	2	2

Замечание. Обратим внимание, что угол между прямыми не обязательно равен , он может быть равен и (рис. 13.7-13.8). Таким образом,

формула (13.16) определяет значение косинуса угла между прямыми с точностью до знака. Косинус острого угла между прямыми l1 и l2 может

быть найден по формуле:

n1 n2

a a

b b

cos(l1;l2 )

(13.17)

Заметим, что l1 l2

n1 n2

a1a2 b1b2

Рис. 13.7

Рис. 13.8

Расстояние от точки до прямой

Пусть на координатной плоскости задана

прямая l : ax by c 0

и точка

M 0 (x0 ; y0 ) l.

Найдем расстояние d от точки M 0

до прямой l.

Очевидно,

что

какова

бы

ни

была точка

M1 (x1 ; y1 ) прямой l (рис. 13.9),

справедливо

соотношение:

Рис. 13.9

M1M0 n

npn M1M0

, где n(a;b) l.

x1 ; y0

y1 .

Поскольку

M1 (x1 ; y1 ) l, то

M1M 0

ax1 by1 c 0

c ax1 by1. Тогда:

a(x0 x1 ) b( y0 y1 )

ax0 by0

( ax

1 by1 )

a2 b2

Таким образом, имеем:

ax0

by0 c

(13.18)

a2 b2

Замечание. Если нормальный вектор прямой n отложен от некоторой точки прямой, то для всех точек M 0 , которые лежат в одной полуплоскости с

концом вектора n d npn M1M0 , а для всех точек, лежащий в другой полуплоскости, d npn M1M 0 . Таким образом, для точек, лежащих в одной

из полуплоскостей, на которые разбивает координатную плоскость прямая, ax by c 0, а для точек другой полуплоскости ax by c 0.

N. Какие из сторон треугольника АВС пересекает прямая a : 3x y 1 0, если A( 1; 0); B(1; 2); C(0;3) ? Найдите расстояние от точки А до прямой а.

Решение.

Подставим координаты точек А, В, С в левую часть уравнения прямой а.

А: 3 1 0 ; В: 3 2 1 0 ; С: 3 1 0.

Значит, точки А и С лежат в одной полуплоскости относительно прямой

а, а точка	В в другой. Таким образом, прямая а пересекает стороны АВ и ВС
треугольника АВС.
	3 ( 1) 0 1
A; a	3 ( 1) 0 1		2	10	.
			2	10

	32 ( 1)2	10		5

Ответ: прямая а пересекает стороны АВ и ВС; A; a 10 5 .

	Уравнение пучка прямых
	Def. Пучком прямых на плоскости с центром в точке
	М называется множество всех прямых плоскости,
	проходящих через точку М (рис. 13.10).
	Отметим, что пучок задается однозначно либо
	своим центром, либо двумя пересекающимися	Рис. 13.10
	прямыми.	Рис. 13.10
	прямыми.

Th. 13.2 Если M 0 (x0 ; y0 ) – центр пучка, то уравнение пучка имеет вид:

a(x x0 ) b( y y0 ) 0		(a, b R)	(13.19)
или
y y0	k (x x0 )	k R.	(13.20)

Доказательство.

Доказательство вытекает непосредственно из формул (13.5) и (13.7). Заметим, что уравнение пучка (13.19) не содержит прямой x x0 .

Th. 13.3	Если	заданы	две	прямые	l1 : a1 x b1 y c1	0	и
	l2 : a2 x b2 y c2 0,		то уравнение пучка имеет вид:
		a1 x b1 y c1		m a2 x b2 y c2 0.		(13.21)
	Причем это уравнение содержит все прямые пучка, кроме l2 .

Доказательство.

1)Докажем, что уравнение (13.21) задает прямую пучка. Для любого m R уравнение (13.21) является уравнением первой степени, а значит, задает прямую.

Если M 0 (x0 ; y0 ) – центр пучка, то a1 x0 b1 y0 c1 0 и a2 x0 b2 y0 c2 0. Значит, координаты M 0 удовлетворяют уравнению (13.21). Таким образом,

прямая, задаваемая уравнением (13.21), принадлежит пучку.

2) Докажем, что в уравнении (13.21) всегда можно подобрать значение параметра m так, чтобы прямая, определяемая этим уравнением, проходила через заданную точку M1 (x1 ; y1 ), т.е выполнялось соотношение:

a1 x1 b1 y1 c1 m a2 x1 b2 y1 c2 0.

Если	M1 l2 , то	a2 x1 b2 y1 c2					0 и			значение m однозначно
определяется по формуле:			m	a1 x1		b1 y1		c1	.
				a x b y				c
				2	1	2	1	2
Если же, M1 l2 , но M1 l1 ,				то m .
N. Составьте уравнение прямой, которая проходит через точку пересечения
прямых	a : 2x 3y 6 0		и	b : x 2 y 2 0						а) параллельно прямой

l : x y 3 0. б) перпендикулярно прямой l : x y 3 0.

Решение.

Искомая прямая принадлежит пучку, который задается прямыми a и b. Запишем уравнение пучка:

2x 3y 6 m(x 2 y 2) 0 .

Или

(2 m)x ( 3 2m) y ( 6 2m) 0.

а) Значение параметра m найдем из условия параллельности искомой прямой и прямой l :

Подставляя найденное значение параметра в уравнение пучка, получаем:x y 4 0 – искомая прямая.

б) Значение параметра m найдем из условия перпендикулярности искомой

прямой и прямой l :

1(2 m) 1(3 2m) 0.

Отсюда m 53 . Подставляя найденное значение параметра в уравнение

пучка, получаем уравнение искомой прямой:

11x 19y 28 0.

Ответ: x y 4 0.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 139 10 11 12 13 > Следующая >>>

Соседние файлы в папке Лекции

#
05.03.20164.22 Mб11Конспект лекций АиГ_ Реутова ИН_ Часть 1.pdf
#
05.03.2016828.8 Кб13Конспект лекций АиГ_ Реутова ИН_ Часть 2.pdf