Elementy_teorii_grafov_2

íà

'(x; y) < (x; y)

äóãå

исх дной пропускной

7. Åñëèспособности),äëÿ äóãèòî(x;вершинуy) вершинаy помечаx íåменьшепомечена,пометк

àf+вершинаxg.

y ïî-

и '(x; y) > 0(поток по дуге ненулевой), то вершину x

помечнаем пометкой f yg.

8. Если помечена

z, то нах дим марш ут прорыва (неко

торые дуги могут проходиться в

обратном ориентации напра

â

ëå

нии), идущий извершинаz по обратным пом ткам, начиная

ð-

øèíû z ( = (x0;xi

; : : :; z), где каждая

кроме x0

имеет

ê

äóãå

пути, увеличивая его вершина1, если дуг

ориенти-

0

изменяем поток по

k

п метку предыдущей вершины этого пути),

дугаждойориеíòè

этогоâана в обрат ом направлении. Перех дим к п. 5.

9. Конец

алгоритма

полученный

поток является наибольшим.

ðîâ íà

â

àï

лении маршрута), или уменьшая его

1, åñëè

Для обоснования алгоритма введем поня ие

азреза транспортной

-

ти. азрезом транспотной сети

назавается мно

ество V дуг

ñåòè,

сти: G , содержащую

источник x ,

G , содержащую

òîê z.

после удаления которых сеть

аспадается

2 компонен

ы связно

Пропу кной способностью

азреза V

называется суммарная про-

пускнаяВ ч стве примера

рассмотрим

идущих

íóþ ñåòü íà ðèñ. 6. Ïî

G .

0

способность

(V) åãî äóã,

из вершин G0

в вершины

z

(на любом пути из x

â z

стьтранспордуга,олоток по ко орой равен ее

íûì

òîê ïî

å

(указан в круглых скобках ок

äóã ñåòè)

ÿ ïîë

пропускной

.

0Åãî

величина

' =11.

Являетсявляетсли он наи

f(x ; x ); (x ;способности)x ; (x ; z ; (x ; x )g (V ) = 11. Совершенно ясно, что

большим? азрез сети V

1

= f(x

; x

); (x

; xz ); (x

; x

)g имеет пропуск-

ную способность (V

0

1

0

2

0

3

=

1

= 12, а пропускная способность разреза V

2

1

4

2

4

2

5

3

2

ñåò ,

потому не может

всякий поток

рох дит через любой

превысить пр пускную

минимальной пропуск

способности.

Поэтому указа ный на рис. 6 поток является наиболь-

øèì. Íî

наибольшая

величиспособностьа потокразрезаможет не достичь минимальной

21

навлива

, ÷òî ýòî

òàê.

собнтиÒнаибольшаяеоремасти азрезаФорда. личинаÔàëêпотокаерсонаавна. Äëÿнаименьшейзаданной транспортнойпропускной с ñå-

Доказательство. Пусть алг ритм пометок остановился, получен

ïî

шина z осталась непомеченной. Обозначим через V

множество дуг,

òîê '

0

V множество помеченных при этом вершин. При этом вер

связывающих

помеченные и непомеченные вершины. Поток

àæ-

дой уге разреза, идущей из G

G , равен ее пропускной спос бности

ê

æäîé

дуге разр за, идущей из G

G , равен 0

÷å áûëà áû

-

мечена

дна из непомеч нных

вершин. Поэтому величина п ток

'z

0

z

иначе была бы помечена одна из непомеченных вершин. Ппоток

получ нный

àë îð òìå

Форда Фалкерсона,

а разрезпоток,

z

0

равна пропускной способности разреза (V ) и, следовательнî,

определяемый

äóãами, связывающèìè ïîìå÷åííûå

непомеченные в

алгоритме вершины, имеет минималь ую величи у.

å

á ëьшего поток ' < m, то при решении задачинаибольший,наибольшем

Для задачи о назначениях возможности работ иков можно зад ть

ó åâîé

R = fr

g (i 2 1; n;

j 2 1; m). Если величина

íàè

мы получаматрицейминимальный разрез H, который дает возможностьпоток-

строить

ij

узкое место следующим образом:

1. Множество L

z

= fij r

2 R;

(x ; y ) 2= Hg определяет группу

работников (строки матрицы R), для которых не хватает работ

ij

0

j

матрицы R, в которых стоят единицы для этих строк).

(столбцовработ олбцы матрицы R), для которых не

ает работников

2. Множе

âî M = fjj r

2 R;

(y ; z) 2= Hg определяет группу

(строк

матрицы

R, в которых стоят единицы для этих столбцов).

Пример

ij

j

ой задачи п иведенхват разделе 3.2, а

примеры решениязадачитранспортназíачениях в разделе

5.1.

3

Задание 8

1. Для гра а задачи 1 задания 7, найти кратчайшее остовное де-

ðåâî:

22

b)	дерева	яснением всех вводимых в						лг ритме обозначений;
	построитьсвести выполнениереализациюалгоðàèòìàà ñäëÿуказаниемзаданногоäëèíãðàреберà и выделениаблицу; -
d)	ем жирными ребрами					кратчайшего остовного дерева;
	строить таблицу				найденногоотцов, сыновей и братьев для описания
	ïîлученного			спискпроверить полученное описание построени-
	ем по нему дерева.				задачу, заданную матрицей						äè
2. ешить
ельност й продукттранспортнуюв пунктах производства, спроса									дуктапроизвопунк-
òàõ	потребления		способностей транспортных перевозпрок:
a)	казать условия, при которых весь							димый продукт может
	óдовлетворить весь спрос продукт						произвоперевозки могут быть осу
	щес влены; построить транспортную							сеть для указанной транс-
	портной	задачи;
b) описать сведение транспортной задачи к задаче о наибольшем
	потоке;
) описать алгоритм решения з дачи о н иб льшем потоке;
e)	по решению задачиалгоритмааибольшем потоке получить матрицу пе-
d	свести выполнение					äëÿ çàäàííîé çàäà			â	аблицы;
3.1	ревозок решение			транспортной задачи.
	Пример задачи на п строение
	кратчайшего остовнîго дерева с ее решением
		кратчайшее остовное дерево для							заданного спис-
комПостроитьребер их длинами:						1,5	8),	2,3ãðà1 à,	2 5	2	2 6
( ({1,2}, 6), ({1,3}, 3), ({1,4}, 9),
({3,7}, 4), ({4,5}, 2), ({4,8}, 1),						({5,9},	7),	({6,7}, 2), ({7,8}, 3), ({8,9},
2),						23

A. Дадим пошаговое описание алгоритма Краскала с описанием

таблицы выполнения:

1

o

м множест

ребер гра а по

анию длин ребер;

o

Сортируаблице выполнения выделяем первую колонку, в которую вы-

2

писываем отсортированные ребра вместевозрастих длиной.

приводя

В порядке

ания длин ребер выбираем ребра,

щие к циклувозрастуже

выбранными

ребрами (в колонкневыбора N

ñò

по порядку номер выбора от 1 до n 1 если рассмат-

ривае

îå

не приводит к

ñ óæ

выбранными, и з

(не большреброчем k = n=2) для

связнос

ãðà à âû-

выбранного ребра уже введеннымциклуомпонентам связности:

авимпротивном случае). Для этого заводим нескольк

êîëîíîàê

бранных ребер

C

; C

2

; : : : и проверяем, при адлежат ли вершины

1

компоненте связно

1) если не принадлежат ни одной

сти, то выбираем это

(â

введеннойвыбо а

àâèì î÷åð íîé

номер выбора), заводим вую олонкпо нту

связности

â ñëåäóþ-

ùåé

äíîé

ребровключаеì

нее вершины этого ребра;

2) еслисвободна из

принадлежит

дной компоненте связности

(нах дится квершинкомпоненты связности),

другая принад-

лежит другой

олонкомпоненте связности, то

бираем

это ребро (в

ëîíê

авим очередной номер выбора) и объединяем

ê мпоненты связности

(переносим вершины второй к

связностивыборапервую, вычеркивая их аккуратно из второйомпонентык -

ненты);

омпоненте связ-

3) если обе вершины ребра принадлежат одной

o

ности, то включение эт го ребра приводит

циклу;

поэтому это

ребро не включаем (в колонку выбора ставим зн

).

составляют кратчайшее осто ное дерево,прекращаемсумма их длин длину

3 Как только n 1 ребро будет выбрано,

выполнение

алгоритма: ребра, помеч нные номерами в

олонке выбора N,

кратчайшего остовного

äåðåâà.

24

	fa; bg; l					N				C	1		C	2		C	3		C	4
	3					1
										2; 3
4 8		1				2				5			64; 68
2 6						3
						4				6
4 5						5				4; 8
6 7		2				6				7
8 9						7				9
1 3		3				8				1
7 8
3 7		4
2		6
5 9		7
5		8
	f1; 4g; 9					равна				15.
Длина полученного	дерева
C. еализация гра а с выделением кратчайшего остовного дерева.

èñ. 9

25

	N				F		S		B
	1				0		3
2					3		5
3					1		2
4					5		8		6
5					2		4
6							7
7					6		9
8					4				0
9					8		0
Построенная ализ ция д	ерева				ïî				ýòîì	у списку отцов, сыновей и
братьев приведена нà ðèñ. 10.

						èñ. 10					åå
3.2 Пример транспортн й задачи
		сведением к задаче о наибольшем потокрешения
			транспортную				, заданную следующей матрицей про-
извопункешитьах			îòðåбления									ных перевозок (0-
		ди ельн ст й продуктзадачув пунктах производства,													продукта
столбец			производительности			(s ; s ; s ; s ) продуктспросаизготовителеé
(			лей) X ; X ; Xспособностей; X , 0-я							транспорок потребности (d ; d ; d
							1	2	3		4	лей) Y ; Y ; Y , элемен-
впроизводитедукте торговых организаций (потð
			1	2	3	4										1	2
ты на пересечении i-й строки (i = 1; 2; 3; 4)ебитеj-го столбца (j = 1; 2; 3)
							26						1	2	3

сведением к задаче о наибольшем потоке и ее решением:

0

15

5

11

2

4

11

4

6

2

8

5

12

3

A. Корректность данной

9

транспортной

задачи определяется следу-

ющими условиями:

dj спрос в продукте всех потребителей равен

1.

P4

si

= P3

i=1

j=1

2.

производимому продукту (10+9+11+8=38=15+12+11);

P3

pij si

i

;

; ; 4) транспортные магистрали позволя-

3.

P

p

d

j 5+2+3=10>9,; ; 3) транспортные магистрали позволяют

(2+5+4=11>10,i

ютj вывезти произведенный продукт от каждого производителя

(2+5+4+5=16>15,

4+6+2=12>11, 5+1+3=9>8);

.

ij

j

доставить продукт каждому потребителю

Ищетс

план перевозок5+2+6+1=13>12,b (i ; ; ; 4;4+3+2+3=12>11)j ; ; 3), при котором

выполняются условия:

ij

а от i-го производителя к j-му потреби-

1. 0 b

ij

p

ij

телю не превосхперевозкдит способности соответствующей транспортной

2.

магистрали;

(i = 1; 2; 3; 4) вывозится весь продукт от каждого

P3

bij = si

j=1

3.

производителя;

= 1; 2; 3) удовлетворяется спрос каждого по-

P4

bij

= dj

(j

i=1

требителя.

сеть следующим образом (рис. 11):

Построим

j+4

введемтранспортнуювх д сетироизводителяx выхо jz.

1. Äëÿ

ê æä ãî

отреб

X

(i = 1; 2; ; 4) введем вершину x

i;

äëÿ

Y (ij

= 1; 2; 3)

введем вершину x

0

27

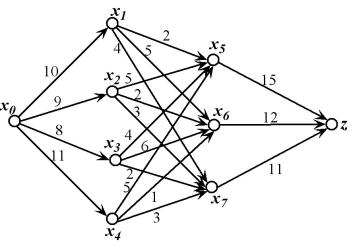
3.пропускнойветственно)Соединим. каждую.способностивершину(x0jx+4; xj+4;i)z)=(j==0ij1+4=; ;z2s;i=3)(10,dсjвыходом9,(15,11,12,8 соответ11z дугойсоот-

4.Соединим каждую вершину xi (i = 1;способности2; 3; 4) каждой вершиной xj+4 (j = 1; 2; 3) дугой пропускной (xi; xj+4) =i;j+4 = pij (соответственно матрице).

èñ. 11

задачи к задаче

íàè-

B. Проведем сведение данной

б льшем

ке для построеннойтранспортной сети. Для этого нужно

ýòîé транспортной сети,

он явля тся наибольшим, а акже, что

ïî

п казать, чòî

решению транспортной задачи строится поток для

Пусть матрица b (i = 1; 2; 3; 4; j = 1; 2; 3) является решением

наибольшему потоку

строится решåние транспортной задачи.

ij

транспортной задачи. Определим ункцию ' на дугах транспортной

сети следующим образом:

j = 1; 2; 3) положим

1. Íà

аждой дуге

(xi; xj+4) (i = 1; 2; 3; 4;

2 поток 'i;j+4

= bij.

; x ) (i = 1; 2; 3; 4)

'

0i

= s .

.

3. На каждой дуге (x0

;iz) (j = 1; 2; 3) положимпоток'

=i d

j+4

28

j+4;z

j

1; 2; 3; 4;

j

= 1; 2; 3) следуют неравенства 0 '

i;j+4

i;j+4

, . .

ункцияне е осходит' на дугахпропускной(xi; xj+4) (способностиi = 1; 2; 3; 4; j = 1; 2; 3) неотрицательнадуг.

Èç ðàâенств '

0i

= s

i

è

0i

= s

i

( = 1; 2; 3; 4) следу

равенство '

0i

=

0i, т. . ункция ' на дугах (x0; xi) (i = 1; 2соответствующих; 3 4) нео рицательна и не

превосходит

пропускной способности

äóã.

'

Из равенств '

= d

è

= d (j = 1;соответствующих2; 3) следу равенство

=

(равна)j = 1; 2; 3), т.

. ункция '

дугах (x ; z) (j

=

j+4;z

j

j+4;z

j

1; 2; 3) неотрицательна

не превосх дит (равíа) пропускной спос б

j+4;z

j+4;z

j+4

Таким образом, ункция

' на каждой дуге транспортной сети неот-

ности

äóã.

рицательнасоответствующихне превосходит пропускной способности этой дуги.

Из равенств '0i

= si

(i

= 1; 2; 3; 4), 'i;j+4

= b j

è

P3

=

si

j=1 bij

= 1; 2; 3; 4) ñë äó

равенство

P3

'i;j+4

= '0i

(i

= 1; 2; 3; 4),

т. е. ункция '

отвечает

условию неразрывности потока в вершинах

x

(i = 1; 2; 3; 4).

j=1

P4

'j+4;z

= dj

(j = 1; 2; 3), 'i;j+4

= bij

è

bij

=

i

Из равенств

dj

(j = 1; 2; 3) следу

равенство

P4

'i;j+4 = 'j+4;z

(j =i=1; 2; 3),

т. е. ункция '

отвечает

неразрывности поток

в вершинах

j Таким

i=1

x

бразом, ункциясловию' каждой вершине транспортной сети

+ 4 (j = 1; 2; 3).

твечает у

неразрывности потока и,

(кроме вхîäà è âûõ äà)

значит, ' является

потоком.

= d

(j

= 1; 2; 3) ñëå

Èç

d

(j = 1; 2словию; 3)

äóãå,

равенствовх дящей

вых д z, максимален и,

j+4;z

j

имеет макси

j

j

åò

j+4;z

=

j+4;z

(j = 1; 2; 3) потому поток на каждой

'

ìàëü óþ

'z

= P3

dj. Мы показали,

что решению транс-

портной

задавеличинусоответствует решение задачиследовательно,наибольшем потоке

для построенной

j=1

ñåòè.

ением з да

àæ

обратное:транспортнойкак потоку ', являющему я

÷è Ïîêà

большем

потоке для ук

ñåòè

построитьрешение

òðàíñ-

è

покажем, что

этогоак

бразазаннойванная матрица b

(i = 1; 2; 3; 4; j

=

ïîðòíой задачи. Для

положим b

ij

= '

i;j+4

(i = 1; 2; 3; 4; j

ij

1; 2; 3) является решением транспортной задачи:

1. Из равенств

i;j+4

= p

ij

(i = 1; 2; 3; 4; j = 1; 2; 3) и неравенств 0

29

b

ij

p

ij

(i = 1; 2; 3; 4; j = 1; 2; 3), которые отвечают требованию

2.

P3

'

+4

= '0i (i =

Èçрешения транспортной'0i = si (i задачи= 1; 2.; 3; 4) è

3.

1; 2; 3; 4)

следуют равенства

P3

bij

= si

(ij=1

1i;j2; 3; 4), которые

Èç

равенств 'j+4;z

= dj (j = ; 2; 3) è

i=1 'i;j+4 = 'j+4;z (j =

j=1

отвечают ребованию 2 решения транспортной задачи.

i=1

P4

bij

= dj

(j = 1; 2; 3), которые

1; 2; 3) следуют равенства P4

отвечают требованию 3 решения транспортной задачи.

Таким образом, условия решения транспортной задачи для матрицы

b

(i = 1; 2; 3; 4; j

= 1; 2; 3) показаны, что завершает сведение эт

ij

задачи к задаче о наибольшем потоке для построенной транспортнîé

ñåòè.

C. Алгоритм Форда-Фалкерсона решения задачи о наибольшем по-

токе состоит

з двух частей:

I.

Получениеx в вых д z,0

i

j+4я дуга, для которой поток по ней равен ее

полного потока

ò. å. òакого ïîòîêà, ÷òî äëÿ ëþá ãî

óòè = (x ; x ; x

; z) (i

2 1; 4; j

2 1; 3), ведущего из входа

II. Увеличение потнайдетск

меток.

пропу0 скной способно ти.

следующий

Для получения полного

потокалгоритмо

1.

нулевые пропускные способнвыполняемсти

=кроме0, оторыеалгоритм:не ассмат-

Все дуги транспортной сети не

мечены,

äóã, êîòî ûå èìå

риваются. Назначается нулевой поток ' = 0 на каждой дуге.

2.

любой путь из входа x0

x;y

в выход z. Если его нет, то пере-

3.

Ищемоди к п. 4 алгоритма.

( ) äóã ïóòè

Находим минимальн ю пропускную способность

min

и на дугах этого пóти увеличиваем поток на эту

8(x; y) : (x; y) 2

! 'x;y = 'x;y + min(величину:)

30