2.4. Метод преобразования координат

Во всех рассмотренных выше задачах выбиралась такая система координат OXY, в которой уравнения кинематики имеют наиболее простой и удобный для решения вид. Однако конечный результат часто бывает необходимо получить в некоторой неподвижной системе координат, в которой рассматривается весь механизм в целом. Кроме того, полученные в подразделе 2.3 выражения не позволяют определять кинематические параметры движения произвольных точек на звеньях механизмов, например, центров масс, рабочих органов и т.п. Все эти проблемы удобно решать методом преобразования координат.

Рассмотрим конкретный пример. Пусть требуется определить кинематическое параметры движения некоторой точки S на шатуне AB (рис. 2.15).

Суть метода. С каждым звеном механизма связывают свою систему координат. На рис. 2.15 OXY – неподвижная система координат (НСК), связанная со стойкой, AX₂Y₂ – подвижная локальная система координат (ЛСК), связанная с шатуном 2 и движущаяся вместе с ним. Координаты (.)S в ЛСК нам известны и в процессе движения они не меняются. Связь между координатами точки, измеренными в разных системах известна из аналитической геометрии, на этом и строится данный метод.

Положение начала ЛСК надо выбирать так, чтобы можно было заранее определить его кинематические параметры движения. Для рассматриваемых примеров координаты (x_A, y_A), проекции скорости (v_Ax, v_Ay) и ускорения (a_Ax, a_Ay) точки A найдём как параметры движения конца кривошипа 1 (см. п. 2.2.1).

x_A = l_ОА cos ₁,

y_A = l_ОА sin ₁,

где l_ОА – длина кривошипа.

v_Ax = – ₁ l_ОА sin ₁,

v_Ay = ₁ l_ОА cos ₁,

где ₁ – угловая скорость кривошипа.

где ₁ – угловое ускорение кривошипа.

Величины ₁, ₁, ₁ должны быть заданы по постановке задачи кинематического анализа.

Ось X₂ ЛСК следует направлять вдоль соответствующего вектора l₂ (см. векторные контуры в п. 2.3) или параллельно ему, ось Y₂ – так, чтобы образовывалась правая система координат.

Кроме того, будем полагать, что предварительно выполнен расчёт методом векторных контуров (см. п. 2.3.1, 2.3.2), и нам известны параметры вращательного движения шатуна 2 ₂, ₂, ₂.

Координаты (.)S в НСК найдём, просто записав связь между координатами точки, измеренными в разных системах координат. В матричной форме она имеет вид:

(2.36)

Последовательно дифференцируя выражение (2.36) по времени, получим зависимости для определения проекций скорости и ускорения (.)S в НСК:

(2.37)

2.5. Общая последовательность кинематического анализа

Рассмотренные выше метод векторных контуров и метод преобразования координат позволяют произвести полный кинематический анализ механизма. Рассмотрим, как эти два метода взаимодействуют на примере 6-звенного механизма, представленного на рис. 2.16.

Общую последовательность кинематического расчета можно представить следующим образом.

1. По исходно заданным кинематическим параметрам движения входного звена определяются параметры движения той его точки, в которой присоединяется 1-я структурная группа.

2. Производятся расчеты для неё и вычисляются параметры движения той точки звена структурной группы, в которой присоединяется следующая.

3. Эти значения преобразуются в систему координат следующей структурной группы, производится её расчет и т.д.

Рассмотрим эту последовательность подробно. Пусть изначально задан угол поворота кривошипа ОА ₀₁ от оси X₀, значение его угловой скорости ₁, и ускорения ₁ в данном положении.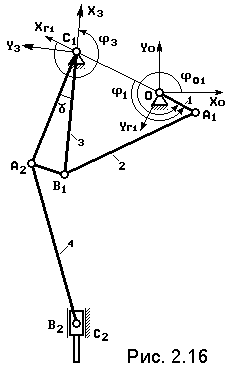

Сначала решаем задачу для контура OA₁B₁C₁, состоящего из входного кривошипа и 3-х шарнирной структурной группы. Решение производим в НСК OX_Г1Y_Г1, естественной для данной группы (см. рис. 2.16). Угол поворота кривошипа в этой системе: ₁ = ₀₁ – ₀₁,

где: ₀₁ – угол поворота системы OX_Г1Y_Г1 от OX₀Y₀

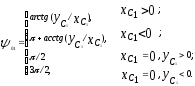
Координаты опоры С₁(x_C1, y_C1) должны быть заданы как конструктивные параметры.

Параметры движения шарнира А₁ определяем так, как это описано в подразделе 2.2. Далее, производим анализ методом векторных контуров, как это описано в п. 2.3.1. В результате находим ₂, ₂, ₂, ₃, ₃, ₃ – параметры вращательного движения шатуна А₁В₁ и коромысла В₁С₁.

Методом преобразования координат (см. подраздел 2.4) находим параметры движения центров масс этих звеньев и точки А₂, в которой присоединяется следующая структурная группа.

Переходим к следующему контуру C₁A₂B₂, рассмотрим его отдельно (рис. 2.17). Он представляет собой 4-х звенный механизм со структурной группой типа “шатун-ползун”. Как показано в п. 2.3.2 решение удобно искать в НСК OX_Г2Y_Г2, поэтому координаты шарнира А₂, проекции его скорости и ускорения, найденные ранее в НСК OX_Г1Y_Г1 следует преобразовать в НСК OX_Г2Y_Г2, тогда контур C₁A₂B₂ решается так, как это описано в п. 2.3.2. В результате находим ₄, ₄, ₄ – параметры вращательного движения шатуна, A₂C₂ и x_C2, v_C2, a_C2 – положение, скорость и ускорение ползуна.

Методом преобразования координат находим параметры движения центров масс шатуна и при необходимости преобразовываем их в НСК X₀Y₀.