ГЛАВА 4

ЭЛЕМЕНТЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ

Во второй главе мы рассмотрели поведение атома в предположении, что на него не действуют посторонние силы. Однако в твердом теле атомы взаимодействуют друг с другом, и этот факт необходимо учитывать при описании различных свойств твердых тел.

Первой удачной попыткой объяснения электрических и магнитных свойств твердых тел была теория свободных электронов Друде (1900 г.). Она исходила из представления, что электроны в твердом теле ведут себя подобно молекулам идеального газа. Это позволило ей объяснить такие явления, как электро- и теплопроводность металлов, термоэлектронную эмиссию, термоэлектрические и гальваномагнитные эффекты и т.д. Однако теория Друде оказалась бессильной при рассмотрении свойств твердых тел, зависящих от их внутренней структуры. Она не давала ответа даже на такой вопрос: почему одни тела являются проводниками, а другие изоляторами.

Следующим этапом в развитии электронной теории стала зонная теория твердых тел.

4.1.Обобществление электронов в кристалле

Втвердом теле расстояния между атомами настолько малы, что каждый из них оказывается в потенциальном поле остальных атомов, которое нельзя игнорировать.

Вначале проведем качественное рассмотрение последствий объединения атомов в кристалл. Для этого сравним состояние изолированного

атома, когда расстояние до другого атома r>>а – порядка кристаллической решетки (рис. 4.1, а). Для простоты возьмем атом натрия, имеющий энергетические уровни 1s, 2s, 2p, 3s. Уровни 1s, 2s, 2p заполнены, уровень 3s содержит один электрон, более высокие уровни пусты. Ато-

75

мы отделены друг от друга потенциальными барьерами, и переход электрона между 3s уровнями отдельных атомов уже на расстоянии более 2 нм практически невозможен.

В верхней части рисунка показана картина распределения плотности вероятности ρ = 4πη2ψψ* обнаружения электрона на расстоянии r от ядра.

Теперь подвергнем атомы медленному сближению так, чтобы образовался кристалл. По мере сближения атомов взаимодействие между ними растет. На рис. 4.1, б приведены два атома натрия.

а)

б)

Рис. 4.1. Атомы натрия: а – удаленный атом, τ>>a; б – два атома, τ>>a

Сближение атомов вызывает уменьшение высоты и толщины потенциальных барьеров, разделяющих атомы. Так, для электронов 3s высота уровня оказывается выше потенциального барьера, и уровень оказывается общим для всех атомов. Это подтверждается и перекрытием функции ρ для 3s уровня. Иными словами, происходит обобществление ва-

лентных 3s электронов.

В кристалле на этом уровне должно разместиться N одинаковых электронов. Однако, согласно принципу Паули, это запрещено, и 3s уровень расщепляется на N подуровней. В итоге формируется энергетическая зо-

76

на, где могут находиться свободные электроны, называемые электронным газом.

Вследствие уменьшения толщины потенциального барьера при сближении атомов некоторую свободу перемещения по кристаллу получают и более близкие к ядру электроны. Некоторые из них могут туннелировать сквозь барьеры, и вероятность перемещения зависит от толщины барьера. Эта вероятность уменьшается для более глубоких уровней. Так, в рассматриваемом кристалле время нахождения на уровне 3s составляет для электрона 10-15 с, а время нахождения на самом глубоком уровне 1s – 104 с.

Вернемся к 3s зоне и рассмотрим ее структуру. Мы уже говорили, что зона состоит из N подуровней. Такое состояние называют N – кратно вырожденным, а расщепление уровня на подуровни – снятием вырождения. Так выглядит ситуация, если мы имеем дело с S уровнем (l = 0). В общем случае кратность вырождения определяется знакомым нам соотношением n = 2l+1 (п. 2.7). Число электронов, которое может размещаться в зоне, определяется выражением (2l+1)n.

Расстояние между подуровнями очень мало. Если ширину зоны Е принять за несколько электрон-вольт, то расстояние между уровнями будет не более 10-22 эВ. Поэтому обычно не учитывают тонкую структуру зоны, считая зону непрерывной.

4.2.Модель Кронига-Пенни

Впредыдущем разделе мы рассмотрели качественную картину обобществления электронов, пользуясь моделью изолированного атома

сучетом постулата Паули. Здесь воспользуемся аппаратом квантовой механики для более строгого решения этой же задачи. В общем случае задача является безнадежно сложной, и приближенное решение ее достигается путем принятия ряда упрощений.

Во-первых, будем считать, что кристалл представляет собой две подсистемы: легкие, быстрые электроны и тяжелые неподвижные ядра. Такое приближение называется адиабатическим. Оно является приемлемым, поскольку за время изменения состояния электронов состояние ядер практически не изменяется.

77

Однако картина остается слишком сложной. Уравнение Шредингера описывает поведение одной частицы, и вторым приближением является одноэлектронное приближение. Оно состоит в том, что электрон представляют в некоем совокупном поле, созданном другими электронами и не зависящем от мгновенного положения данного электрона.

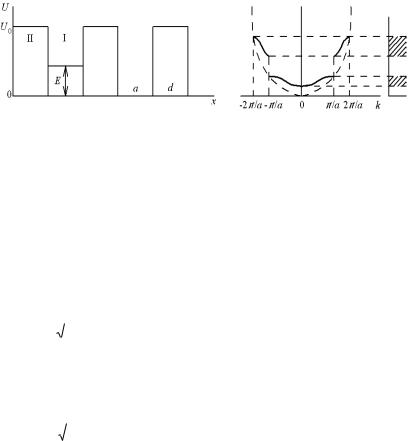
Модель потенциального поля кристалла представляет собой линейную цепочку прямоугольных потенциальных ям глубиной U0, разделенных потенциальными барьерами (рис. 4.2, а). Ширина ямы b, ширина барьера d, b+d = a – период решетки.

E

в

d

в

d

E

а

d

x

-2π/а -π/а 0

π/а 2π/а k

а)

б)

Рис. 4.2. Электрон в кристалле: а – модель Кронига-Пенни; б – энергетический спектр электрона

Запишем стационарное уравнение Шредингера

		d 2					k 2 0 .									(4.1)
		dx 2
	Решение этого уравнения имеет следующий вид:
	в области ямы
	ψ1 = А1exp(ik1x)+B1exp(-ik1x),															(4.2)
	где k				1
										2mE ,						(4.3)
	1
	в области барьера
	ψ2 = А2exp(k2x)+B2exp(k2x),															(4.4)
							1
	где k		2								2m(E U		0	) .		(4.5)
	78

Очевидно, что решение уравнения (4.1) будет определяться величиной U0. Различают три случая, или три приближения.

Приближение свободных электронов. Потенциал решетки очень мал, U00, т.е. мы имеем электрон в нулевом потенциальном поле. Этот случай практически совпадает с уже рассмотренным в п. 2.3. Напомним, что движение электрона описывается плоской волной, а энергетический спектр является сплошным, т.е. представляет собой одну разрешенную зону. Потенциальное поле кристалла можно представить как большую яму с плоским дном.

Приближение сильносвязанных электронов. Это другой крайний случай, когда пренебрегают влиянием решетки, а U0 = Ua – потенциал атома. Этот случай также рассмотрен в п. 2.7. Энергетический спектр электрона в этом случае линейчатый, т.е. разрешенные зоны вырождаются в энергетические уровни, а электроны локализованы в атомах.

Приближение слабосвязанных электронов. Это приближение в некотором роде описывает промежуточный случай между двумя предыдущими: приближением свободных и сильносвязанных электронов. Потенциальное поле этого приближения можно представить в виде суммы

U(x) = U0+ δU

где δU << U0 – периодическая функция с периодом, равным периоду кристаллической решетки.

Модель потенциального поля кристалла в этом случае можно представить в виде потенциальной ямы со слабо рифленым дном. Решение уравнения Шредингера для такого поля называют функцией Блоха. Для одномерного случая она имеет вид:

ψ(x) = U(x)exp(ikx),

(4.6)

где U(x) – периодическая функция, или модулирующий множитель, описывает характер дна потенциальной ямы.

Подставив (4.2) и (4.4) в выражение (4.6), можно найти конкретный вид модулирующего множителя U(x). Если учесть граничные условия для предельного случая потенциального барьера (d0, U0∞), можно получить выражение

P sin k1a	cos k a cos ka ,	(4.7)
k1a	1

79