Kosevich A.M. The crystal lattice (2ed., Wiley, 2005)(ISBN 3527405089)(342s)_PSa_

190 7 Interaction of Excitations in a Crystal

The dispersion law may be decaying also due to strong anisotropy of isofrequency surfaces. Even if in each direction of k-space the condition ∂2 ω/∂k2 < 0 is satisfied, but the isofrequency surface is not convex (the cross section of such a surface is shown in Fig. 4.1) a decay such as t → t + t may be allowed.

When both longitudinal (l) and the transverse (t) phonons participate simultaneously in a three-phonon process, the conditions for its realization, i. e., the conditions for satisfying (7.2.3) to be met, are much simplified even if the dispersion laws of each type of phonons are nondecaying. To analyze these processes, we consider the dispersion laws (7.2.4) in view of the condition (7.2.5). One can see that for a onedimensional model the processes l → t + t and l → l + t (Fig. 7.4) are possible, while processes such as t → l + l , t → t + l are forbidden, at least in the isotropic approximation.

Fig. 7.4 Fulfillment of the dispersion laws for the decays l → t + t (on the left) and l → l + t for a 1D model.

Fig. 7.5 Three-phonon process t1 → l + t2 .

However, taking into account the existence of two kinds of transverse phonons (t1 and t2) with different sound velocities (s1 = s2 ) the following process is possible (Fig. 7.5):

t1 → t2 + l, s2 < si < sl .

7.3 Inelastic Diffraction on a Crystal and Reproduction of the Vibration Dispersion Law 191

We emphasize that the phonon dispersion law anisotropy assists significantly when the condition (7.2.3) is satisfied, although it does not remove all prohibitions arising in the isotropic approximation.

In conclusion we note that for all processes of single-phonon decay into two phonons there are corresponding inverse processes (fusion of two phonon into a single one). These are allowed or forbidden to the same extent as direct processes.

7.3

Inelastic Diffraction on a Crystal and Reproduction of the Vibration Dispersion Law

In elucidating the conditions for Bragg X-ray (rather soft γ-quantum) reflection, we considered the crystal as an ideal spatial lattice of fixed mathematical points. However, the scattering by a real crystal whose atoms can perform vibrational motion are distinguished from the scattering by fixed centers. First, the incident wave may excite vibrational motion in the crystal, i. e., generate phonons in it. Then, the vibrating lattice atoms are displaced from their equilibrium positions and the scattering by such a system is different from that by an ideal periodic structure (the incident wave interacts with crystal phonons). The second distinction is connected with the root-mean-square value of the displacement.

Let us discuss the first of the phenomena generated by the inelastic interaction of penetrating radiation with a vibrating crystal. In a kinematic theory, the probability of the incident beam scattering with its wave vector changing to q = q2 − q1, is proportional to the squared modulus of the following integral over the sample volume (Section 0.4.5):

U(q2, q1 ) ≡ V(q) = U(r) exp (−iqr) d3r,

(7.3.1)

where U(r) is the potential of the crystal interaction with a field or with a particle. In a monatomic lattice

U(r) = ∑U0 [r − r(n) − u(n)] ,	(7.3.2)
n

and U0 (r − ξ) describes the interaction between the penetrating radiation and a single atom at the point ξ. We substitute (7.3.2) into (7.3.1)

V(q) = F0 (q) ∑exp {−iq [r(n) + u(n)]} .

(7.3.3)

n

Here the notation F0 (q) is introduced for the atomic scattering factor

F0 (q) = U0 (r)e−iqr d3r.

The sum over the lattice sites that is a multiplier in (7.3.3) will be called the structure factor and is denoted as S(q). Usually the structure factor is determined as this sum divided into the number of crystal sites N.

192 7 Interaction of Excitations in a Crystal

We try to calculate the structure factor using the smallness of atomic displacements. As, by assumption, u a and we take interest in the wave vectors q whose modulus does not exceed the order of magnitude of π/a, we expand each term of the structure factor as a power series of u, restricting ourselves to the linear terms

S(q) = ∑e−iq[r(n)+u(n))] = ∑e−iqr(n) − iq ∑u(n)e−iqr(n).			(7.3.4)
n	n	n

The first term on the r.h.s. of (7.3.4) describes the diffraction pattern for an ideal periodic structure (Section 0.5). It gives the amplitude of scattering by a crystal for which q = G, where G is any reciprocal lattice vector.

It is essential that the crystal state under this scattering does not change.

We now study the second (linear in displacement) term on the r.h.s. of (7.3.4), having denoted it as M(q). To understand the physical meaning of this term in the structure factor, we consider M(q) as an operator in occupation-number space and express the displacement vector u(n) through the phonon creation and annihilation operators (6.1.16)

M(q) = −iq ∑u(n)e−iqr(n) = −i						h¯	1/2
						2mN
		n					(7.3.5)
× ∑	qe(α, k)		∑	a	(k)e−i(q−k)r(n) + a†		(k)e−i(q+k)r(n) .
		ωα(k)		α		α
kα			n

On summing n with (0.4.14) taken into account, it is clear that in (7.3.5) there are terms of two kinds. Some of them involve the operator ak as a multiplier and describe the scattering process accompanied with the absorption (annihilation) of a phonon with the quasi-wave vector k, so that

q2 − q1 = k + G.

(7.3.6)

The other terms involve the operator a†k as a multiplier and are responsible for the phonon radiation (creation) obeying the dispersion law

q1 − q2 = k + G.

(7.3.7)

The matrix elements of the operator M(q) thus determine the amplitude of inelastic scattering involving one phonon (the amplitude of a one-phonon process). It follows from (7.3.6), (7.3.7) that one-phonon scattering may take place either as an N- or a U-process.

We now obtain fairly straightforward energy conservation laws that govern the processes (7.3.6), (7.3.7) and also look at the one-phonon scattering from another point of view. Since we regard V(q) as the energy operator of crystal interaction with an incident beam, the probability of the beam scattering in the first-order perturbation theory is expressed through the squared matrix element f |V(q)| i for a transition from the

7.3 Inelastic Diffraction on a Crystal and Reproduction of the Vibration Dispersion Law 193

initial crystal state i with a set of occupation numbers for phonons {Nk } into the final state f with the occupation numbers Nk . Let Ei and Ef be the crystal energy in the harmonic approximation before and after scattering:

	Ei = ∑	Nα(k) +	1	h¯ ωα(k),	Ef = ∑	Nα(k) +	1	h¯ ωα(k).
			2				2
	kα				kα

Furthermore we introduce the notation where E1 = E(hq¯ 1 ) and E2 = E(hq¯ 2 ) for the energies of an incident particle (γ-quantum, electron or neutron) before and after scattering, and E( p) is the energy of a scattered particle as a function of its momentum.

In the first Born approximation, the probability of the separate scattering by a crystal in the state i is proportional to

w(q, E) = ∑|

f | V(q) |i |2 δ(E + Ef − Ei),

(7.3.8)

f

where E = E2 − E1 = h¯ ω.

Using the integral representation of the δ-function

1

+∞

δ(z) =

exp(izt) dt,

2π

−∞

and transforming (7.3.8) we obtain

1

+∞

i(Ef − Ei )t

w =

e

iωt

∑| f | V |i |

2

exp

dt.

(7.3.9)

2πh¯

h¯

−∞

f

We take into account the identity

∑| f | V |i |

2

exp

i(Ef − Ei)t

= ∑ f |V| i

f |V| i exp

i(Ef − Ei)t

h¯

h¯

f

f

= ∑ f V† i f e h¯i Ht Ve− h¯i Ht i = ∑ i V† f f |V(t)| i ,

f

f

where we move to the Heisenberg representation of the operators and denote V by V(0). Then,

		1	+∞
	w(q, E) =		V (q, 0)V(q, t) eiωt dt.	(7.3.10)
		2πh¯

−∞

Here we use the notation . . . for the quantum-mechanical average in some crystal state, {Nk }. We note that by virtue of time homogeneity

V (q, 0)V(q, t) = V (q, −t)V(q, 0) .

(7.3.11)

194 7 Interaction of Excitations in a Crystal

We come back to the definition (7.3.3), taking into account (7.3.11)

w(q, E) =	1	|F0 (q)|	2	∑ e	iq[r(n)	−	r(n )]
	2πh¯
				n,n

+∞	(7.3.12)

×eiqu(n,t)e−iqu(n ,0) e−iωt dt.

−∞

Thus, in the general case the scattering probability is determined by the Fourier components of the correlation functions

eiqu(n,t)e−iqu(n ,0) . (7.3.13)

For small thermal atomic displacements and insignificant changes in the wave vector in the scattering, we confine ourselves to the expansion (7.3.4). This expansion is sufficient to describe the one-phonon processes of inelastic scattering. Using the definition (7.3.5), we note that

M†(q, t) = M(q, 0) = 0,

and calculate the part quadratic in M(q) that contributes to the inelastic scattering probability

1

+∞

δw(q, E) =

F

(q)

2

M†(q, t)M(q)

e−iωt dt

2πh¯

| 0

|

−∞

(7.3.14)

+∞

qj ql

=

2

∑

j

l

(n , t) e

iq[r(n)

−

r(n )]

−

iωt

|F0 (q)|

u

(n, t)u

dt.

2πh¯

n,n −∞

The average value coincident with the pair correlator (6.4.1) has arisen in the integrand of (7.3.14). Thus, the probability of one-phonon inelastic processes is proportional to

	δω(q, E) = N |F0 (q)|2 qj ql Kjl (q, ω),				(7.3.15)
	where			+∞
		1
	Kjl (q, ω) =		∑ Φjl (n, t)eiqr(n)−iωt dt.		(7.3.16)
		2πh¯
			n	−∞

Thus, the specificity of the scattering of various particles (or waves) is manifest in the presence of the atomic factor F0 (q) only.

The participation of the crystal structure of substances in the generation of onephonon processes is universal and determined by the pair displacement correlator. The

7.3 Inelastic Diffraction on a Crystal and Reproduction of the Vibration Dispersion Law 195

probability of such processes (7.3.15) is proportional to a spatial and a time Fourier transformation of the displacement correlator (6.4.2).

It follows from (6.4.2) and (7.3.16) that

Kjl(q, ω) = 1 ∑ ej(k)el (k) {Nα(k)δ [ω − ωα(k)]

2mN kα ωα(k)

(7.3.17)

× ∑ei(q−k)r(n) +	Nα(k) +	1	δ [ω + ωα(k)] ∑ei(q+k)r(n)},
		2
n			n

showing that the Fourier components of the displacement correlation are nonzero only for the frequencies ω = ±ωα(k). This means that one-phonon processes are allowed if one of the conditions

E2 − E1 = h¯ ωα(k),	(7.3.18)
E1 − E1 = h¯ ωα(k)	(7.3.19)

is satisfied (we remember that in (7.3.15) h¯ ω = E2 − E1 ).

It is easy to understand from (7.3.17) that the process (7.3.18) is allowed under the condition (7.3.6), and the process (7.3.19) under the condition (7.3.7). The conservation laws (7.3.6), (7.3.7), (7.3.18), (7.3.19) describe the interaction of strange particles (capable of propagating a crystal) with phonons, i. e., the quasi-particles of a crystal.

The inelastic diffraction phenomenon accompanied by one-phonon processes described provides an effective method for describing lattice dynamics. Let us suppose that it is possible to create a narrow beam of particles incident on the crystal, to fix the directions of scattered particles and to measure their energy. Thus, in each scattering process we know q1, q2 , E1 and E2 . If we neglect the umklapp processes whose contribution can be singled out, we determine the values of k and h¯ ω for a phonon participating in the process. Considering various directions and orientations of the crystal, we can reproduce in principle the function ω = ω(k).

However, this experiment will be a success only if with the wavelength of the order of a lattice constant (λ a) one can observe the change in the energy of a beam or a particle by an amount of the order of phonon energy,

δE h¯ ωD h¯ ωm 0.01 eV.

The energy of X-rays with the required wavelength has the order of magnitude

E = h¯ ω = 2πhc¯λ 2πhc¯a 104 eV.

Thus, using X-rays the indicated energy change δE is impossible to observe. But for neutrons,

E =	p2		(2π)2h¯ 2	(2π)2	h¯ 2
		=				0.1 eV,
	2m		2mλ2		ma2

196 7 Interaction of Excitations in a Crystal

which corresponds to the energy of thermal neutrons. Phonon absorption or emission changes the neutron energy by δE, a value that can be observed.

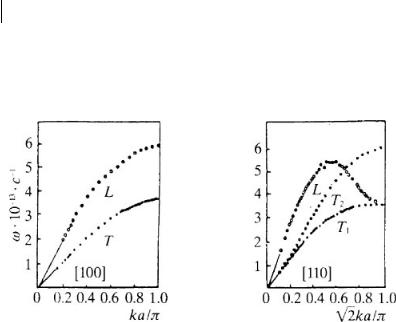
Examples of experimentally reproducing dispersion laws for neutron scattering are given in Figs 2.4b, 3.2, 7.6.

Fig. 7.6 Dispersion curves for the two directions in Al are reproduced by the neutron experiments (Yarnell et al. 1965).

7.4

Effect of Thermal Atomic Motion on Elastic γ-Quantum-Scattering

In distinguishing in (7.3.12) the probability of inelastic one-phonon processes, we have restricted ourselves in (7.3.12), only to the terms containing multipliers qiqk ui (n, t)uk(n , 0) . We have not taken into account the terms with multipliers such as

[qu(n, t)]2 = [qu(n, 0)]2 ,

(7.4.1)

that also have second order of smallness in u(n). These terms were omitted since they contribute to the elastic scattering of penetrating radiation only (for definiteness, we shall speak of γ-quanta). Indeed, the averages (7.4.1) are time independent and, therefore, after the integration over time they lead to the δ-function δ(ω) = h¯ δ(E1 − E2 ) appearing in (7.3.12).

Thus, terms such as (7.4.1) determine the difference between the elastic γ-quantum diffraction intensity from a vibrating crystal from that on an immobile spatial lattice of atoms. It is easily seen that for a quantitative description of the influence the atomic motion on producing elastic diffraction it is not necessary to restrict ourselves to approximation, which is quadratic in displacements.

We remind ourselves that (6.5.9) is applicable for a monatomic lattice

eiqu(n,t) = eiqu(n) = e−W ,

7.4 Effect of Thermal Atomic Motion on Elastic γ-Quantum-Scattering 197

	where	1
	W =			(qu)2 ,	(7.4.2)
		2
	and represent the correlation function (7.3.13) in the form of two terms
	eiqu(n,t)e−iqu(n ,0)	= e−2W			(7.4.3)
	+ eiqu(t)e−iqu(0)	−		eiqu(t) e−iqu(0) .

We begin to analyze this formula with the second term. In the approximation quadratic in displacements it is equal to the average M+ (q, t)M(q, 0) that was considered in calculation of the probability for one-phonon inelastic scattering (7.3.14). It is clear that the next term following the expansion of the second term in (7.4.3) in even powers of the displacement determines the probabilities for multiphonon inelastic scattering processes.

The first term in (7.4.3) is time independent and is thus related to elastic scattering. When substituted in (7.1.3), it contributes to the elastic scattering probability.

The diffraction intensity observed in an experiment is automatically averaged over all the initial crystal states, which is equivalent to a thermodynamic averaging of the scattering probability. On performing a thermodynamic averaging in (7.3.12), we find that the intensity of the elastic γ-quantum diffraction is proportional to the

wel (q, E) = N e−2W δ(E) |F0 (q)|2 ∑eiqr(n)

n

(7.4.4)

= NΩ0 e−2W δ(E) |F0 (q)|2 ∑δ(q − G),

G

where the summation is over the reciprocal lattice vectors; Ω0 is the unit cell volume of the reciprocal lattice. The factor e−2W describing the weakening of the diffraction maxima intensity due to thermal atomic motion is called the Debye–Waller factor.

Since the Debye–Waller factor in (7.4.4) is a multiplying factor, the thermal atomic motion in the crystal does not result in a smearing of the sharp diffraction maxima in γ-quantum scattering it only reduces its intensity.

The generalization of (7.4.4) to the case of a polyatomic lattice is straightforward

wel (q, E) = NΩ0 δ(E) ∑e−Ws Fs(q)eiqxs	∑δ(q − G),	(7.4.5)
s	G

where xs is the vector of the basis of a polyatomic lattice that gives the s-th atom position in the unit cell; es is the polarization vector of the s-th sublattice vibrations,

Ws =	1	∑	{qes(α, k)}2	coth	h¯ ωα(k)	.	(7.4.6)
	2ms N		ωα(k)
		kα			T

198 7 Interaction of Excitations in a Crystal

Examining the processes of the interaction of the γ-quantum with the crystal has shown that an incident γ-quantum may either give the crystal some momentum to produce a phonon or get from the crystal some momentum generated by the phonon “absorption”. In this case the γ-quantum energy will change to a finite value and the scattering will be inelastic.

But another interaction with a crystal is possible when the finite part of the γ- quantum momentum is transferred to a crystal in the process without the phonon emission or absorption. As a result of this interaction, the crystal does not change its state and the γ-quantum conserves its energy. So we have a process without recoil characterized by extremely narrow diffraction lines. The proportion of such elastic processes is measured by the Debye–Waller factor.

7.5

Equation of Phonon Motion in a Deformed Crystal

The equations of crystal lattice motion have static inhomogeneous solutions with boundary conditions determined by external loads. When such crystal states are described in terms of long waves, we can consider the inhomogeneous static deformations that deform the crystal lattice (Fig. 7.7). If the deformations are small, they are solutions to the linear equations of elasticity theory. Static deformations do not influence small vibrations (phonon after quantization) due to the linearity of the elastic theory equations, but including the anharmonic interactions transforms a deformed lattice into an inhomogeneous elastic medium.

It is of interest to discuss the possibility to describe the vibrations of such spatial inhomogeneous crystals in terms of phonons. Let us suppose that the macroscopic crystal characteristics vary essentially at distances of the order of δL. How is this inhomogeneity to be taken into account, while preserving the usual concept of phonons?

The phonons were introduced to quantize vibrations of the homogeneous crystal that results in the fact that the states of an individual phonon were characterized by a quasi-wave vector k. If the distance δL is large compared to the average phonon

wavelength ¯ , the phonon concept may be preserved in an inhomogeneous

δL λ

crystal, too. Indeed, to describe the crystal vibrations with the above inhomogeneities instead of normal modes, one should take the wave packets with the interval of wave vectors δk, where

>	1	¯
δL	δk	λ.	(7.5.1)

Analyzing (7.5.1) and taking into account the relation between the wavelength and the value of the wave vector we obtain δk k, implying that the wave packets concerned consist of normal modes whose wave-vector differences much less than their wave vectors. Some conclusions important for further discussion follow from the last assertion.

7.5 Equation of Phonon Motion in a Deformed Crystal 199

First the wave packet described may be associated with a vibration with the quasiwave vector k, i. e., with an individual phonon in a state with a given k.

Then, the velocity of this new “phonon” is determined by the group velocity of the packet:

v =	∂ω	.		(7.5.2)
	∂k
	¯		δx	δL, then a
First, if we measure the spatial positions within δx, where λ

phonon1, having a quasi-wave vector k and located at the point r can be introduced. Under such conditions the crystal-state inhomogeneity manifest in the inhomogeneity of a “refraction coefficient” for a phonon, i. e., in the dependence of phonon frequency on the coordinate r: ωα = ωα(k, r). The vector k of the corresponding packet will

then vary in time
	dk	= − ω(k, r) ≡ −	∂ω
				.	(7.5.3)
	dt		∂r

The approximation in which the relation (7.5.3) is meaningful corresponds completely to the Eikonal approximation in geometry optics. By analogy with the description of electromagnetic vibrations in inhomogeneous media, we can describe the equations of motion for a sound beam that follows directly from (7.5.2), (7.5.3)

dr	=	∂ω(k, r)		dk	= −	∂ω(k, r)
			,				.	(7.5.4)
dt		∂k		dt		∂r

The equations of motion (7.5.4) can be derived not only using the wave properties of phonons employed to construct the wave packets. According to the de Broglie principle the phonon is a quasi-particle with energy h¯ ω and quasi-momentum p = h¯ k. Thus, the energy h¯ ω(k, r) can be regarded as the Hamiltonian function and (7.5.4) as the Hamiltonian form of the equations of motion of this quasi-particle.

In the case of small elastic deformations the dependence of ω(k, r) on the strain

tensor uik is linear
ω(k, r) = ω0 (k) + gil(k)uil (r),	(7.5.5)

where ω0 (k) is the dependence of frequency on a quasi-wave vector in a nondeformed crystal.

It is interesting to analyze (7.5.5) and the equations of motion (7.5.4) near the edge of the phonon frequency band. We shall the quasi-wave vector from the value of km corresponding to the maximum or minimum (if we speak of optical phonons) value of ω0 (k). Then, at small k

1

ω0 (k) = ωm − 2 γilkikl . (7.5.6) Confining ourselves to small k, in (7.5.5) we obtain

ω(k, r) = ωm + gil(0)uil (r) −	1	γilkikl ,	(7.5.7)
	2

where ωm is the frequency band boundary of the continuous spectrum of a nondeformed crystal.

1) The condition δkδx 1 is allowed by the inequality (7.5.1).