
- •Глава 1. Краткие сведения из элементарной математики. 6
- •Глава 2. Элементы высшей математики. 8
- •Глава 3. Применение дифференциальных уравнений первого порядка для решения прикладных задач физики, биологии, медицины 25
- •Глава 1. Краткие сведения из элементарной математики.
- •1. Функция
- •1.1. Способы задания функции
- •1.2. Основные элементарные функции.
- •2. Логарифмы и их свойства
- •Глава 2. Элементы высшей математики.
- •2.1. Механический смысл производной.
- •4. Функция нескольких переменных.
- •4.1. Частные производные.
- •4.2. Полное приращение и полный дифференциал.
- •4.3. Примеры для самостоятельной работы
- •5. Неопределенный интеграл.
- •5.1. Первообразная и неопределенный интеграл
- •5.2. Свойства неопределенного интеграла.
- •5.3.Таблица интегралов
- •5.4. Интегрирование методом замены переменного или способом подстановки
- •5.5.Интегрирование по частям
- •6. Определенный интеграл
- •6.1. Основные свойства определенного интеграла.
- •6.2. Вычисление определенного интеграла. Формула Ньютона – Лейбница.
- •6.3. Применение интегралов для решения количественных медицинских задач
- •7. Дифференциальные уравнения. Введение. Постановка задачи
- •7.1. Дифференциальные уравнения первого порядка (общие понятия)
- •7.2. Дифференциальные уравнения с разделенными и разделяющимися переменными
- •Глава 3. Применение дифференциальных уравнений первого порядка для решения прикладных задач физики, биологии, медицины
- •Глава 4. Краткое введение в теорию комплексных чисел
- •Глава 5. Дифференциальные уравнения второго порядка
- •1. Линейное однородное дифференциальное уравнение
- •1.1. Алгоритм решения дифференциального уравнения
- •1.2.Примеры решения дифференциальных уравнений
- •Глава 6. Применение дифференциальных уравнений для исследования колебательных процессов
- •1. Состояние динамических систем вблизи положения равновесия
- •2. Дифференциальное уравнение механических колебаний
- •Глава 7. Математическое моделирование в биологии и медицине
- •1. Модель Вольтерра
- •2. Фармакокинетическая модель
- •3. Простейшая математическая модель эпидемии
- •4. Простейшая модель инфекционного заболевания
4. Функция нескольких переменных.
Рассматривая функции одного переменного,
мы не сказали, что при изучении многих
явлений приходится встречаться с
функциями двух и более переменных.
Например, площадь прямоугольника
![]() ,
где каждой паре значенийxи y
соответствует одно определенное
значение S.
Следовательно, функцияSявляется функцией двух аргументов или
функцией двух переменных.
,
где каждой паре значенийxи y
соответствует одно определенное
значение S.
Следовательно, функцияSявляется функцией двух аргументов или
функцией двух переменных.
Функция
![]() ,где
каждому изменениюnнезависимых аргументов соответствует
одно значение функции называется
функциейn
переменных.
,где
каждому изменениюnнезависимых аргументов соответствует
одно значение функции называется
функциейn
переменных.
4.1. Частные производные.
Пусть zявляется функцией двух переменных:![]() .
Если один из аргументов, например,xизменяется на
.
Если один из аргументов, например,xизменяется на![]() ,
а остальные аргументы остаются
неизменными, то мы имеем частное
приращение.
,
а остальные аргументы остаются
неизменными, то мы имеем частное
приращение.
![]() .
.
Также определяем частное приращение при изменении аргумента yпри не изменяющемся аргументеx.
![]() .
.
Определение 5.Частной производной функции z
по аргументу x
называется предел отношения частного
приращения
![]() к приращению
к приращению![]() при стремлении
при стремлении![]() .
.
Частная производная может обозначаться:
![]()
Следовательно, согласно определению имеем две частные производные.
![]()
![]() .
.
Если мы имеем некоторую функцию nнезависимых переменных, то и частных производных в общем случае будем иметьn.
Пример:
![]() ,
т. е. Мы имеем функцию четырех переменных
,
т. е. Мы имеем функцию четырех переменных![]() .
Найдем все частные производные этой
функции.
.
Найдем все частные производные этой
функции.
![]() .
.
4.2. Полное приращение и полный дифференциал.
Пусть дана функция
![]() .
Полное приращение имеет вид:
.
Полное приращение имеет вид:
![]() .
.
Полным дифференциалом данной функции называется выражение
![]() ,
,
где dx и dy –дифференциалы независимых переменных.
Понятие полного дифференциала может быть распространено на функцию любого числа независимых переменных.
Если дифференциалы независимых переменных
достаточно малы, то можно считать, что
полный дифференциал функции равен
приближенно приращению функции:
![]() .
Зная также, что
.
Зная также, что![]() и
и![]() ,
можно записать формулу для полного
приращения:
,
можно записать формулу для полного
приращения:![]() .
.
4.3. Примеры для самостоятельной работы
1.![]() Найти
полный дифференциал для следующих
функций:
Найти
полный дифференциал для следующих
функций:
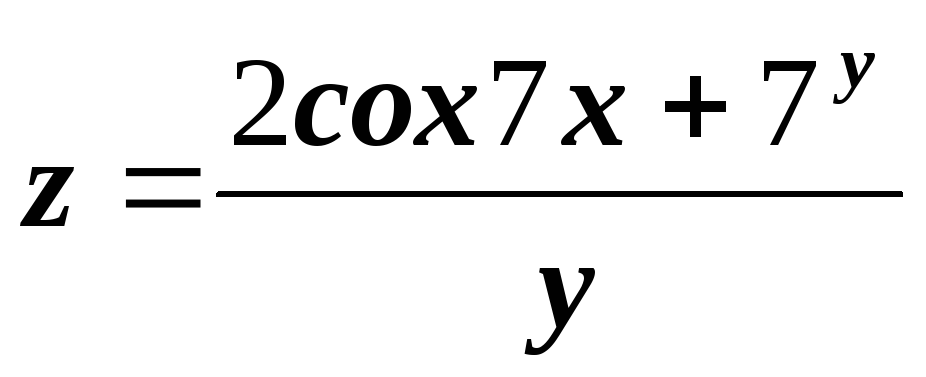 4)
4)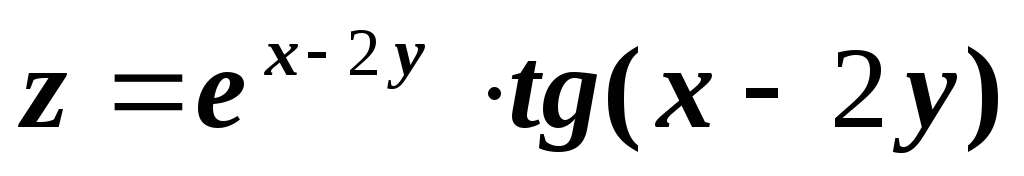
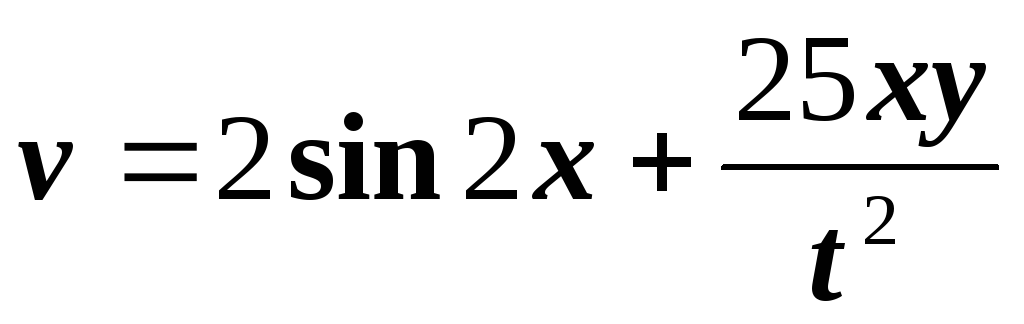 5)
5)
 6)
6)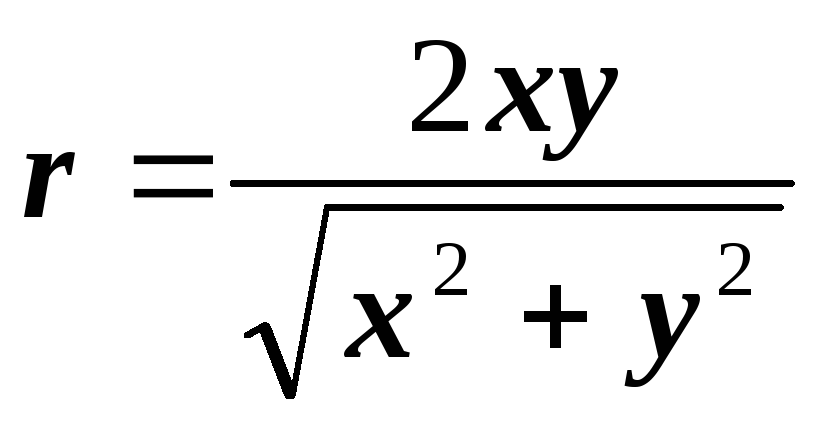
2. Вычислить полное приращение функции z, если дано:
![]() ,
,![]() ,
,![]() ,
,
![]()
5. Неопределенный интеграл.
5.1. Первообразная и неопределенный интеграл
Пусть дана функция
![]() ,
которая является производной некоторой
функции
,
которая является производной некоторой
функции![]() ,
т. е.
,
т. е.![]() .Необходимо
найти функцию
.Необходимо
найти функцию![]() .
Если такая функция существует, то она
есть первообразная от данной функции
.
Если такая функция существует, то она
есть первообразная от данной функции![]() .
.
Определение
6. Функция![]() называется первообразной от функции
называется первообразной от функции![]() на отрезке
на отрезке![]() ,
если во всех точках этого отрезка
выполняется равенство
,
если во всех точках этого отрезка
выполняется равенство![]() .
.
Пример. Найти первообразную от функции
![]() .
.
Из определения первообразной следует,
что функция
![]() является первообразной, так как
является первообразной, так как![]() .
.
Очевидно, что если для данной функции
f(x)
существует первообразная, то она
не является единственной, так как в
качестве первообразных могут быть
следующие функции:
![]() ,
гдеС- произвольная постоянная, так как
,
гдеС- произвольная постоянная, так как![]() .
.
С другой стороны, не сложно доказать,
что функциями вида
![]() исчерпываются все первообразные от
функции
исчерпываются все первообразные от
функции![]() .
.
Определение 7.Если функция![]() является первообразной для
является первообразной для![]() ,
то выражение
,
то выражение![]() называется неопределенным интегралом
от функции
называется неопределенным интегралом
от функции![]() и обозначается символом
и обозначается символом![]() .
.
Таким образом, по определению
![]() ,
если
,
если![]()
![]() .При
этом функцию
.При
этом функцию![]() называют подынтегральной функцией, а
называют подынтегральной функцией, а![]() -подынтегральным выражением.
-подынтегральным выражением.
Итак, согласно выше изложенному
неопределенный интеграл представляет
собой семейство функций![]() .
.
С геометрической точки зрения неопределенный интеграл представляет совокупность кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т. е. вдоль оси Оy.
Зададимся вопросом: для всякой ли
функции
![]() можно найти первообразные, а,значит,
и неопределенный интеграл? Оказывается,
что не для всякой. Более того, если
производная от элементарной функции
всегда является элементарной функцией,
то первообразная от элементарной функции
может оказаться и не представимой с
помощью конечного числа элементарных
функций.
можно найти первообразные, а,значит,
и неопределенный интеграл? Оказывается,
что не для всякой. Более того, если
производная от элементарной функции
всегда является элементарной функцией,
то первообразная от элементарной функции
может оказаться и не представимой с
помощью конечного числа элементарных
функций.
Определение 8. Нахождение первообразной для данной функции называется интегрированием
