1.1. Алгоритм решения дифференциального уравнения

Если дано дифференциальное уравнение вида

y+ p y +q y = 0,

необходимо:

1. Написать характеристическое квадратное уравнение

k² + p k + q = 0

2. Найти корни этого уравнения

,

3. Записать общее решение данного дифференциального уравнения в виде:

, если k₁k₂ - действительные

, если k₁=k₂ - действительные

, если корни комплексные k_1,2 =   i

, если корни мнимые k_1,2 =  i

4. Найти частное решение, удовлетворяющее начальным условиям, если таковые заданы.

1.2.Примеры решения дифференциальных уравнений

Пример 1. Дано уравнение

y+ y - 2 y = 0.

Характеристическое уравнение имеет вид:

k² + k - 2 = 0.

Находим корни характеристического уравнения:

,k₁ = 1 ,k₂ = -2 .

Общее решение данного дифференциального уравнения имеет вид:

.

Пример 2. Дано уравнение

y 4 y + 4 y = 0.

Характеристическое уравнение имеет вид: k² - 4k + 4 = 0 k₁ = k₂ = 2

Записываем общее решение

Пример 3. Дано уравнение

y 2 y + 5 y = 0.

Напишем характеристическое уравнение:

k² + 2k + 5 = 0

k₁ = -1 + 2i

k₂ = -1 - 2i

Следовательно, общее решение имеет вид

Пример 4. Дано уравнение

y+ 9 y = 0.

Найти общее и частное решение, удовлетворяющее начальным условиям

y|_x=0 = 0 ; y |_x=0 = 3

Решение: напишем характеристическое уравнение

k² + 9 = 0

Находим корни

k₁ = 3i; k₂ = - 3i

Общее решение есть:

Найдем частное решение. Предварительно определим первую производную.

Постоянные C₁ иC₂определяются из начальных условий

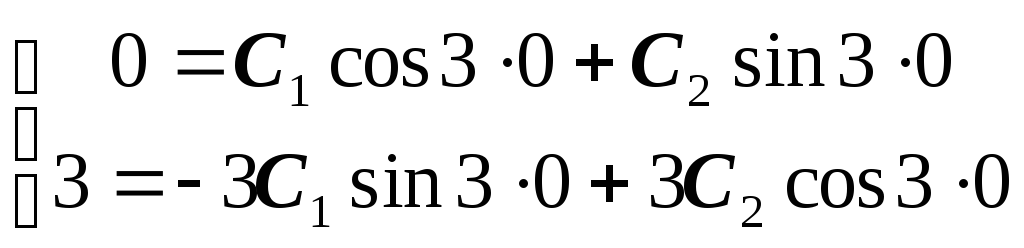
Мы получили систему двух уравнений с двумя неизвестными. Нетрудно определить, что C₁=0, C₂=1.

Следовательно частное решение данного дифференциального уравнения имеет вид: y = sin 3x

Пример 5. Дано уравнение

Найти общее и частное решение, удовлетворяющее начальным условиям.

при.

Напишем характеристическое уравнение и найдем его корни

Корни действительные и равные, следовательно общее решение имеет вид

Найдем, исходя из начальных условий, С₁и С₂

Следовательно, частное решение имеет вид

Глава 6. Применение дифференциальных уравнений для исследования колебательных процессов

1. Состояние динамических систем вблизи положения равновесия

Дифференциальные уравнения второго порядка используются во многих областях естествознания.

Остановимся на рассмотрении движения динамических систем вблизи положения равновесия, т.е. на колебаниях. При достаточно малых отклонениях от положения равновесия колебания бывают обычно гармоническими.

Ограничим наше рассмотрение только случаем свободных колебаний без учета сил трения и внешнего воздействия.

П

а б в г

Рис.6. Колебательные системы. (а – математический маятник, б – пружинный маятник, в – шарик на дне сферической чашки, г – электрический колебательный контур).

L

C

римеры свободных колебаний в различных системах

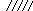
Во всех приведенных примерах сила, действующая на систему (шарик), выражается сложной функцией его отклонения от положения равновесия. ,

где x– малое отклонение от положения равновесия, а- точка устойчивого равновесия.

Сила f(x)в точке равновесия равна нулю, т. е. f(0)=0.

Обычно в реальных физических системах отличным от нуля бывает член . Так какx=0 есть точка устойчивого равновесия, сила должна быть направлена к точкеx=0. Это значит, что.

Исходя из второго закона динамики, запишем уравнение движения для малых отклонений от положения равновесия.

или , где.

Выражая ускорение a через вторую производную смещения x по времени, получаем

Разделим обе части уравнения на массу mи обозначим.

После проведенных преобразований получаем уравнение гармонических колебаний для механических систем .

(*)

Получим такое же уравнение для случая электромагнитных колебаний. Э.Д.С. индукции в колебательном контуре, имеет вид

.

Учитывая, что , снова приходим к дифференциальному уравнению второго порядка. Разделим обе части уравнения наи обозначим.

Окончательно получаем для электромагнитных колебаний

(**)

Примечательно, что, несмотря на различную природу механических и электромагнитных колебаний, они описываются одинаковыми дифференциальными уравнениями второго порядка, уравнениями гармонических колебаний. Разница лишь в том, что во втором уравнении мы вместо (смещения) имеем дело с электрическим зарядом, и стремление к равновесию - есть стремление восстановить нулевое значение заряда на конденсаторе.

Найдем решение уравнения гармонических колебаний. Составим характеристическое уравнение .

Его корни мнимые и равны соответственно:

Следовательно, решением данного уравнения в случае механических колебаний функция будет выглядеть так:

,- постоянные интегрирования.

После несложных преобразований можно упростить это выражение

.

Аналогично, можно записать для электромагнитных колебаний

Здесь введенная ранее величина - есть собственная циклическая частота колебаний,(или) – амплитуда колебаний,- начальная фаза.