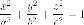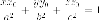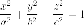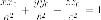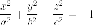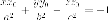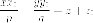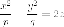- •Парабола.
- •Директориальна свойство параболы
- •Относился к притче.
- •Оптическая свойство параболы.
- •Фокусное свойство эллипса
- •Директориальна свойство эллипса
- •Уравнение касательной к эллипсу
- •Оптическая свойство эллипса
- •Фокусное свойство гиперболы
- •Директориальна свойство гиперболы
- •Уравнение касательной к гиперболе.
- •Оптическая свойство гиперболы.
- •Поверхности вращения
- •Поверхности переноса.
- •Цилиндры.
- •Прямолинейные образующие на поверхности однополостного гиперболоида
- •Прямолинейные образующие на поверхности гиперболического параболоида
- •Касательная плоскость
- •Свойства симметричной матрицы
- •Самосопряжённых оператор в евклидовом пространстве
- •Диагонализации квадратичной формы ортогональным преобразованием координат
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •Приведение общего уравнения поверхности второго порядка к каноническому виду
Прямолинейные образующие на поверхности гиперболического параболоида
Рассмотрим уравнение гиперболического параболоида:
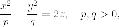
для
удобства сделаем замену  и
и Тогда
уравнение запишется в виде
Тогда
уравнение запишется в виде
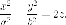
Разложим на множители:
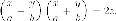
Аналогично с предварительными соображениями получаем уравнения двух семей прямолинейных образующих гиперболического параболоида:
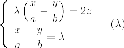 и
и 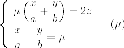
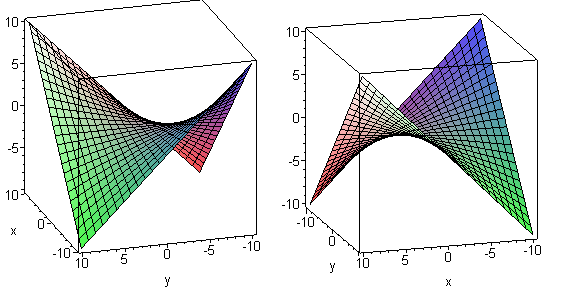
Теорема. На поверхности гиперболического параболоида лежат две семьи прямых, которые имеют следующие свойства:
через любую точку гиперболического параболоида проходит ровно одна прямая с каждой семьи ;
любые две образующие из разных семей пересекаются;
любые две прямые с одной семьи является скрещивающимися;
любые три прямые с одной семьи параллельные некоторой плоскости.
Доказательство можно посмотреть в методичке.
Пример. Найдите
уравнение плоскости, параллельной
плоскости 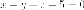 и
пересекает гиперболический
параболоид
и
пересекает гиперболический
параболоид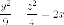 по
двум прямолинейным образующим. Найдите
канонические уравнения этих образующих.
по
двум прямолинейным образующим. Найдите
канонические уравнения этих образующих.
Запишем
уравнение параллельной плоскости 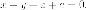 Найдем
ее пересечение с гиперболическим
параболоидом.
Найдем
ее пересечение с гиперболическим
параболоидом.

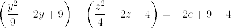
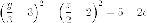
Эта
кривая второго порядка распадается на
пару прямых, которые пересекаются,
если 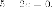 есть
есть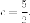 Итак
плоскость, которую мы ищем, имеет
уравнение
Итак
плоскость, которую мы ищем, имеет
уравнение Две
прямые, лежат в этой плоскости и является
пересечением с параболоидом:
Две
прямые, лежат в этой плоскости и является
пересечением с параболоидом:
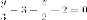 и
и 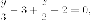
или 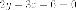 и
и 
Уравнения этих прямых в пространстве:
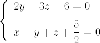 и
и 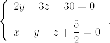
Найдем канонические уравнения. Для первой прямой:
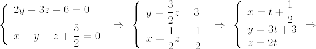
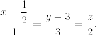
Для второй прямой:

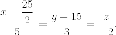
Касательная плоскость
Воспользуемся некоторыми знаниями по математическому анализу.
Если
поверхность задана неявным уравнением -
точка на ней, то есть то уравнение
касательной плоскости к поверхности в
этой точке: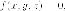

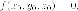

Здесь - частные
производные по соответствующей переменной
в данной точке
Вектор 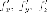
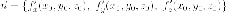 -
вектор нормали к поверхности в
точке
-
вектор нормали к поверхности в
точке 
Найдем уравнение касательной плоскости к эллипсоида

в
точке 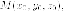 принадлежащей
эллипсоида.
принадлежащей
эллипсоида.
Найдем частные производные:
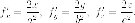
Воспользуемся уравнением касательной плоскости к неявно заданной поверхности:

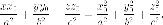
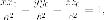
поскольку
точка 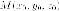 принадлежит
эллипсоида.
принадлежит
эллипсоида.
Аналогично
можно записать уравнение касательных
плоскостей к другим поверхностям второго
порядка в точке 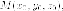 принадлежащей
поверхности:
принадлежащей
поверхности:
|
|
уравнение поверхности |
уравнение касательной плоскости |
|
эллипсоидной |
|
|
|
однополостный гиперболоид |
|
|
|
двуполостные гиперболоид |
|
|
|
эллиптический параболоид |
|
|
|
гиперболический параболоид |
|
|
Заметим, что с эллипсоидом, двуполостные гиперболоидом и эллиптическим параболоидом касательная плоскость имеет единую общую точку - точку касания и поверхность находится по одну сторону от касательной плоскости. Касательная плоскость пересекает однополостный гиперболоид и гиперболический параболоид по паре прямолинейных образующих; поверхность находится по разные стороны от касательной плоскости.
Пример. Через
прямую 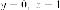 проведите
плоскости, касаются двуполостные
гиперболоида
проведите
плоскости, касаются двуполостные
гиперболоида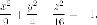 и
определите точки соприкосновения.
и
определите точки соприкосновения.
Плоскости,
проходящие через прямую, образуют пучок
плоскостей. Запишем его
уравнения: 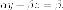 Запишем
уравнение касательной плоскости к
двуполостные гиперболоида в неизвестной
точке
Запишем
уравнение касательной плоскости к
двуполостные гиперболоида в неизвестной
точке принадлежащей
поверхности:
принадлежащей
поверхности:

Нужно
найти такую точку на поверхности, в
которой касательная плоскость принадлежит
пучка плоскостей 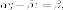 есть:
есть:


Поскольку точка принадлежит поверхности, то
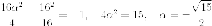
Итак касающиеся плоскости имеют уравнения
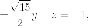
соответствующие
точки соприкосновения 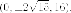
Ортогональная диагонализации матрицы квадратичной формы
Рассматриваем евклидово
пространство  с
ортонормированным базисом
с
ортонормированным базисом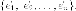 Каждому
вектору
Каждому
вектору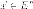 с
координатами
с
координатами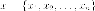 поставим
в соответствие матрицу
поставим
в соответствие матрицу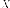 размера
размера или
вектор-столбец
или
вектор-столбец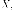 по
правилу:
по
правилу:
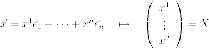
Скалярное
произведение двух
векторов  и
и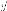 в
ортонормированном базисе можно записать
в виде
в
ортонормированном базисе можно записать
в виде
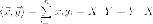
где 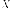 и
и вектор-столбцы,
образованные из координат соответствующих
векторов.
вектор-столбцы,
образованные из координат соответствующих
векторов.
Рассмотрим линейное
пространство  вектор-столбцов
(матриц размера
вектор-столбцов
(матриц размера ).Зададим
в этом пространствескалярное
произведение по
формуле
).Зададим
в этом пространствескалярное
произведение по
формуле

Будем
говорить, что вектор-столбцы 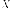 и
и взаимно
ортогональны, если
взаимно
ортогональны, если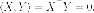
Напомним несколько определений.
Пусть - матрица размера Число называется собственным
числом матрицы если
существует ненулевой вектор-столбец такой
что
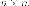

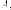
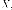

Вектор-столбец 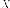 называетсясобственным
вектором матрицы
называетсясобственным
вектором матрицы 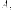 соответствующий
собственному числу
соответствующий
собственному числу
Число  является
корнем характеристического
уравнения
является
корнем характеристического
уравнения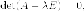 которое
является многочленом
степени
которое
является многочленом
степени относительно
относительно Корни
этого многочлена могут быть комплексными. Но
если
Корни
этого многочлена могут быть комплексными. Но
если симметричная матрица (
симметричная матрица (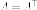 )
с действительными элементами, то ситуация
упрощается.
)
с действительными элементами, то ситуация
упрощается.