21

Министерство образования Российской Федерации

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра МКМК

МЕТОДИЧЕСКОЕ ПОСОБИЕ

По курсу «Ресурс и надежность изделий из композиционных материалов»

Пермь 2011.

Составитель: Р.Я.Газизов

УДК 539.3

Методическое пособие по курсу «Ресурс и надежность изделий из композиционных материалов»./ Сост.:Р.Я.Газизов. Перм. гос. техн. ун-т, Пермь, 2011 – 21с.

В методическом пособии изложены теоретические основы и приведена схема поверочного расчета на надежность по критериям прочности двухопорной балки неоднородного сечения. Даны варианты заданий. Пособие рекомендуется для самостоятельных занятий.

Табл. 1, ил. 8.

Рецензент к.ф.-м.н. Зайцев А.В.

Пермский государственный

технический университет,2011

Рассмотрим «традиционный» расчет на прочность в детерминированной постановке.

Например, в методе расчёта по предельным состояниям максимальная действующая нагрузка (точнее напряженно-деформированное состояние, вызванное этой нагрузкой) сравнивается с нагрузкой, соответствующей предельному состоянию, которое определяет несущую способность конструкции. Несущая способность конструкции – наступление предельного напряженно-деформированного состояния, которое соответствует потере работоспособности конструкции или её разрушению. К таким предельным состояниям относятся: появление пластических деформаций, потеря статической устойчивости, разрушение.

В общем случае можно записать

, (1)

где: –функция, характеризующая предельные возможности конструкции;

–функция, характеризующая реальное состояние конструкции.

Например, пусть зависит от механических характеристик материала конструкции:

,

где – предел прочности;– коэффициент Пуассона; – модули упругости соответственно первого и второго рода. Тогда функция зависит от напряжений, возникающих в элементах конструкции при нагружении:

В общем случае предельные состояния могут быть связаны не только с прочностными характеристиками конструкции, но и с другими свойствами (траектория движения тела, геометрические характеристики и т.д.).

Традиционные методы расчета по предельным состояниям и по допускаемым напряжениям в явном виде не учитывают возможные случайные разбросы, т.е. не учитывается вероятностный характер предельных состояний конструкции или вероятностный характер реального состояния конструкции. Поэтому оценивать работоспособность конструкции логичнее не по детерминированным неравенствам типа (1), а по вероятности выполнения этих неравенств, т.е.

, (2)

где – вероятность безотказной работы.

Введем понятие надежности системы которая оценивается вероятностью выполнения неравенства (1):

. (3)

Под надежностью понимается способность машин, приборов и конструкций безотказно работать в течение определенного отрезка времени. Безотказной работой технических объектов считается выполнение ими всех своих функций в заданных условиях эксплуатации/1/.

Чтобы найти вероятность , надо знать совместный закон распределения случайной величиныпри известных законах распределенияи. Если известно, то

(4)

Для получения численных значений надо знать (определить) закон распределения случайной величиныфункционально зависящей от двух непрерывных случайных величини:

(5)

при известном их совместном законе распределения плотности вероятности .

В общем случае закон распределения случайной величины имеет следующий вид:

. (6)

Математическая задача определения сводится, таким образом, к решению двукратного интеграла

.

Для случая, когда , интеграл берётся по области(Рис. 1), где, поэтому, фиксируяи полагая, получаем конкретные пределы интегрирования, т.е.

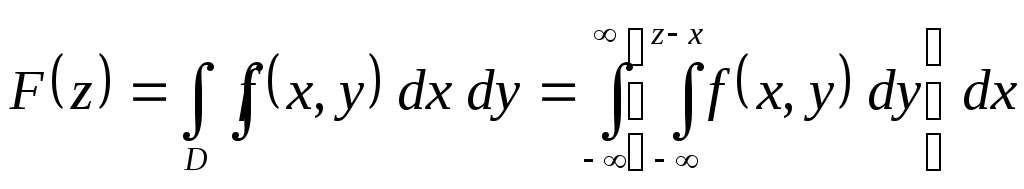. (7)

Плотность распределения получим, дифференцируя (7) по, которая входит как параметр в верхний предел интеграла

. (8)

Так как случайные величины иравноправны, то можно было исключать не, аи получить ещё одно выражение для закона распределения плотности вероятности:

. (9)

Если инезависимы, то плотность распределенияравна

, (10)

или

.

Проинтегрировав правую часть (10) по , получим функцию, зависящую от.

При определении вероятности безотказной работы требуется найти функцию распределения случайной величины, равной разности двух случайных величини:

При известном совместном законе распределения , т.е.

.

На рис.2 показана заштрихованная область, где . Поэтому интегрирование по области, как и в предыдущем случае, можно заменить интегрированием попри фиксированном, а затем по:

. (11)

Дифференцируя (11) по , получим

.

Если случайные величины инезависимы, то имеем

, (12)

или, изменяя порядок интегрирования,

.(13)

Рассмотрим случай, когда иимеют нормальные распределения:

; (14)

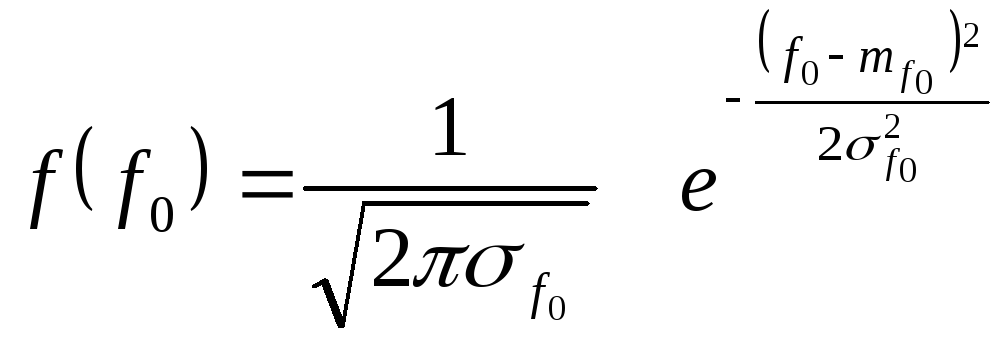; (15)

Закон распределения случайной величины (12) в этом случае равен

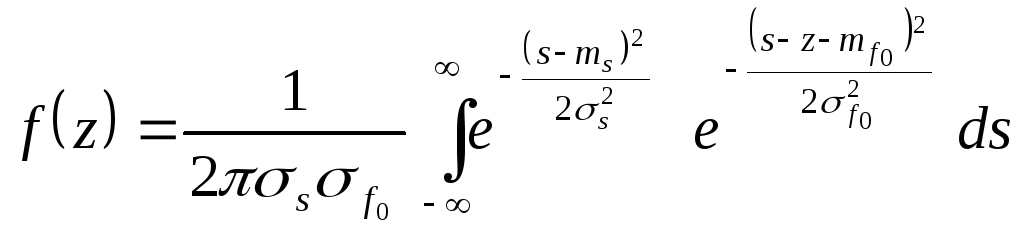; (16)

или

,

где

; ;.

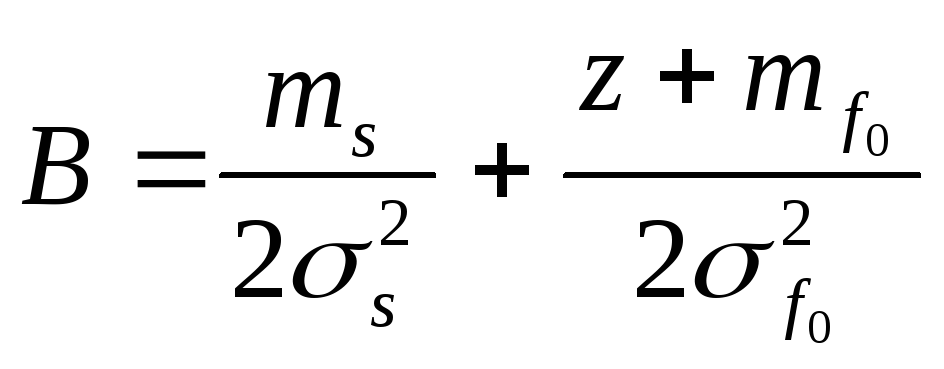Воспользовавшись табличными значениями для определённых интегралов, получаем

,

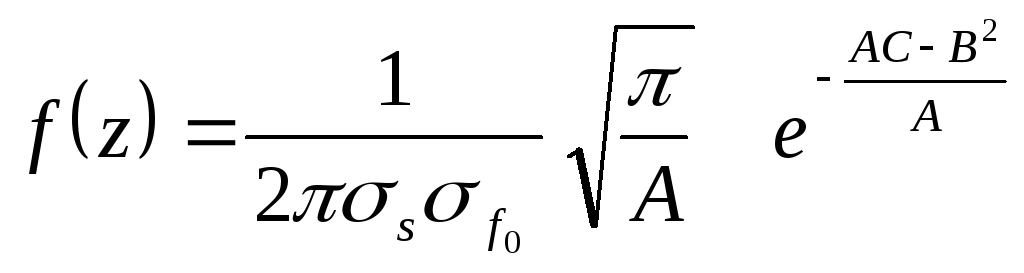или, после преобразований,

, (17)

Где .

Определив , находим вероятность безотказной работы (надёжность)

. (18)

Введя новое обозначение

,

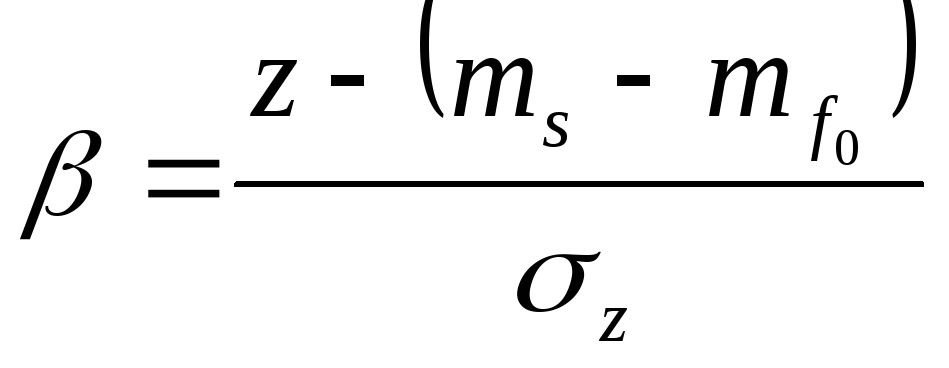получим

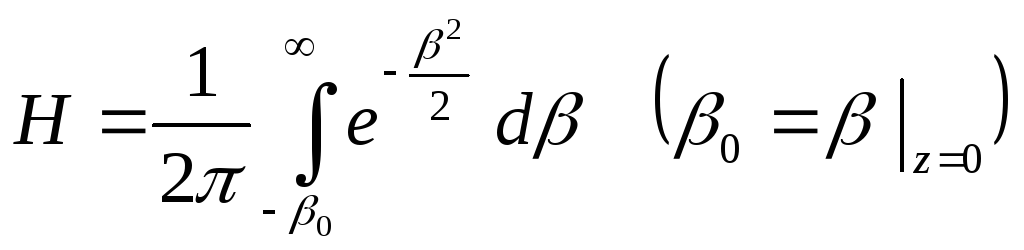. (19)

График подынтегральной функции показан на рис.3. Функция симметрична относительно вертикальной оси, поэтому

Окончательно числовое значение надёжности

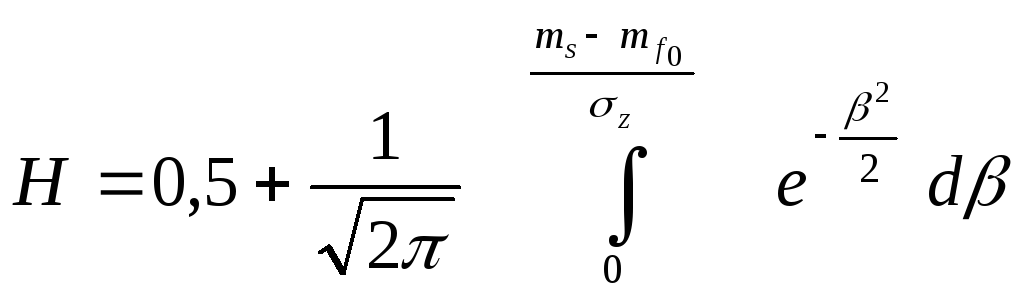. (20)

Интеграл, входящий в правую часть (20), является табличным интегралом («интеграл вероятности»).

Пусть распределение несущей способности (прочности) подчиняется нормальному закону с плотностью вероятности математическим ожиданием прочностии среднеквадратическим (стандартным) отклонением, и распределение сил (нагрузки) подчиняется нормальному закону с плотностью вероятности, математическим ожиданием усилияи среднеквадратическим (стандартным) отклонением(рис. 4).

Функцию надёжности такой системы определяют, используя зависимость/1/:

, (21)

где – нормированная нормальная функция распределения (см. таблицу приложения).

Оценим надёжность двухопорной балки сложного сечения (Рис.5). На рисунке представлена схема нагружения, эпюры поперечных сил и изгибающих моментов.

наиболее опасное сечение.

В системе СИ .

Рассмотрим поперечный изгиб неоднородной балки с сечением вида:

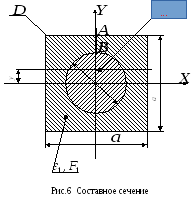
где жёсткость (модуль Юнга) и площадь материала 1, исоответственно характеристики материала 2. Коэффициенты Пуассона примем одинаковыми.

Из курса прикладной механики известно/2/:

, где – напряжения, возникающие вследствие действия изгибающего момента –;радиус кривизны;расстояние от центральной линии (ось ОХ) до произвольного сечения. Тогда:

(22)

Здесь имоменты инерции относительно осичастей составного сечения.

Если рассматривать моменты, как обобщённую силу, а кривизну , как обобщённую деформацию, то связь между этими величинами:

(23)

будет определяться «эффективной» жёсткостью на изгиб . Напряжения в материале 1 и 2 находятся из соотношений:

(24)

Самыми опасными будут напряжения растяжения на наиболее удалённых от нейтральной оси точках сечения. В материале 1(2) соответственно точки А и В:

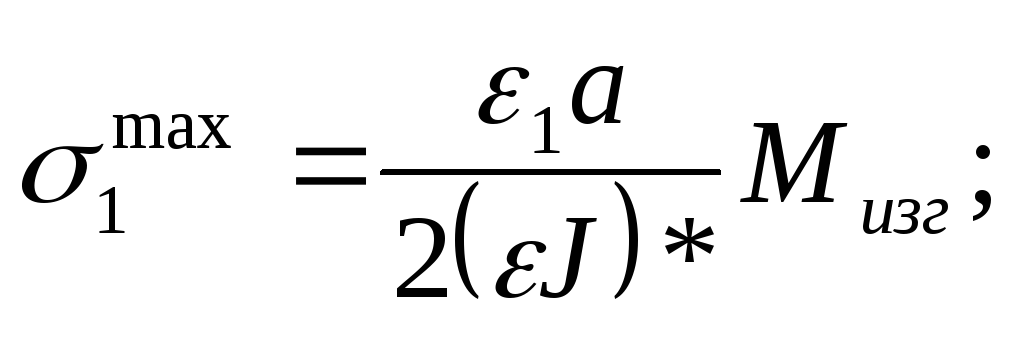
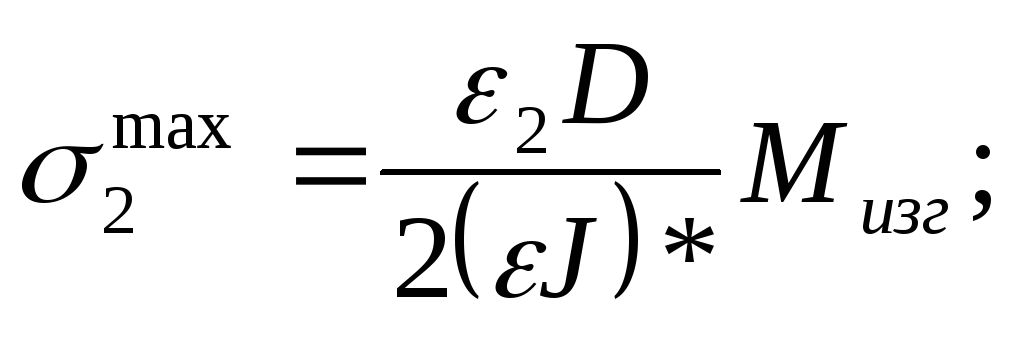(25)

Оценим надёжность (вероятность безотказной работы) составной балки в наиболее опасном сечении при следующих параметрах материалов балки:

Материал 1 – сталь 35Х: ,.

Материал 2 – алюминиевый сплав ,.

Найдём момент инерции:

; .

«Эффективную» жёсткость:

Максимальные напряжения в 1 и 2 материале будут равны:

Примем, что внешние нагрузки и соответственно расчётные напряжения определяем с 10% погрешностью:

Оценим надёжность в 1 материале (точка А):

,

по таблице приложения находим .

В материале 2 (точка В):

,

по таблице приложения находим .

Надёжность составного сечения оцениваем как для последовательной схемы соединений, тогда:

.