4.3.2. Энтропия объекта с непрерывным распределением состояний

Если в качестве объекта рассма­тривать резистор, сопро­ти­вле­ние которого принимает ряд слу­чай­ных значений в ин­тер­вале от а до b (непрерывное распре­де­ление состо­я­ний, рис. 4.6), то непре­рыв­ное распределение можно заменить дискретным. Для этого область изменения сопротивления резистора разбивается на n одинаковых интервалов . Тогда энтро­пия объекта

,

где Р(R_i)  вероятность сопро­тивле­ния резистора в интервале со сред­ним значением R_i. С учетом плотно­сти распределения f(R_i )

и

(4.27)

Раскрывая логарифм произведения, приведем последнее выражение к виду

Перейдя к пределу при , найдем выражение для энтропии объекта с непрерывным распределением параметров:

(4.28)

При выводе формулы (4.28) учитывалось следующее, вытекающее из определения плотности вероятности условие:

.

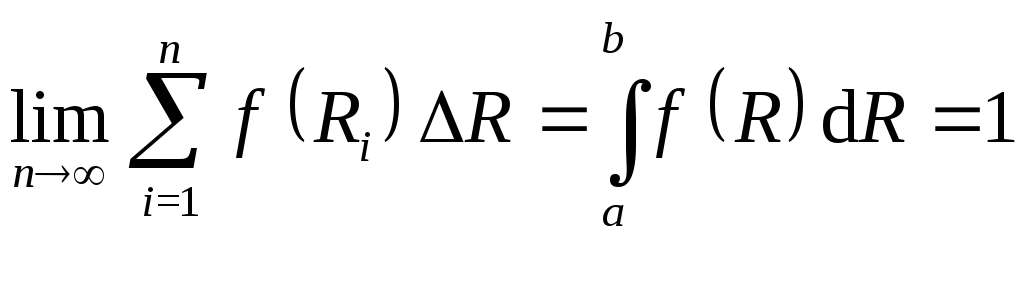Принципиальной особен­ностью энтропии объекта с непрерывным распределением состояний является ее зависимость от шага квантования . Выбор шага квантования обусловлен требуемой точностью при аппроксимации непрерывного распре­деления ступенчатым (дискретным), но само существование шага квантования связано с физической сущностью непрерывного процесса.

Величину в равенстве (4.28) можно рассматривать как начало отсчета энтропии; для многих задач оно оказывается несущественным. В общем случае объект с непрерывным распределением состояний характеризуется параметром х, изменяющимся в пределах, тогда

(4.29)

Последнее равенство можно записать через математическое ожидание M_x случайной величины

(4.30)

Пример 4.3. Определим энтропию объекта, состояния которого (значения х) подчиняются закону нормального распределения (рис. 4.7, а). С учетом плотности распределения х, заданной выражением

,

энтропия (4.30) принимает следующий вид:

Так как , то

(4.31)

Отметим, что энтропия в данном случае не зависит от среднего значения параметра и определяется отношением.

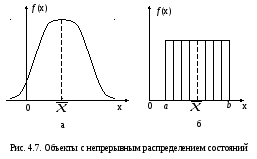
Пример 4.4. Определим энтропию объекта, состояния которого равновероятны на участке (рис. 4.7,б). В этом случае

Из формулы (4.29) получаем:

(4.32)

4.3.3. Определение количества информации по результатам диагностирования

Поясним количество информации, получаемой при диагностировании, на следующем примере. Объект находится в одном из двух равновероятных состояний – работоспособном или неработоспособном, т.е. Р₁ = Р₂ = 0,5; . Допустим также, что работоспособность объекта оценивается по двум параметрам – температуре и давлению. Известно, что при поступлении сообщения от датчика температуры об изменении температуры менее чем на 40^О С объект находится в работоспособном состоянии с вероятностью Р = 0,5. При поступлении сообщения от датчика давления о том, что оно больше 0,15 МПа, можно с вероятностью Р = 1 гарантировать работоспособное состояние объекта. Какое из этих сообщений несет больше информации? Очевидно, второе, так как оно полностью устраняет неопределенность состояния объекта. Подобные соображения позволяют определить величину информации как разность неопределенностей (энтропий) объекта до и после диагностирования.

Если начальная энтропия объекта равна , а после диагностирования она составляет, то информацияJ, полученная в результате диагностиро­вания, равна

. (4.33)

В приведенном примере начальная энтропия объекта

После получения сообщения от датчика температуры вероятности состояний стали , и энтропия объекта

Информация, полученная в результате диагностирования, бит. После получения сообщения от датчика давления вероятности состояний стали, и энтропия объектабит, т.е. информация, полученная в результате диагностирования,

Рассмотрим влияние точности измерения на количество получаемой информации. Пусть параметр Х измеряется с точностью , которая, в свою очередь, определяется шагом квантования. Известно, что до измерения параметрХ находился в интервале . Энтропия такого состояния в соответствии с формулой (4.32). После измерения с точностьюустановлено, что значения параметраХ находятся в интервале . Энтропия второго состояния (после измерения) определяется выражением. Информация, полученная в результате измерения,.

Таким образом, если в результате диагностирования достоверно известно, что измеряемый параметр находится в интервале (точность определения измеряемой величины), то количество полученной информации возрастает с уменьшением погрешностиизмеряемого параметра.