15. Сотня

Нумерация и сравнение чисел в пределах 20. Вначале повторяются некоторые вопросы нумерации чисел до 10: получение следующего числа натурального ряда прибавлением числа 1, сравнение соседних чисел, имена чисел в устной и письменной нумерации. Обращается внимание учащихся на то, что имена чисел от О до 9 не связаны друг с другом: для обозначения чисел от О до 9 на письме используются особые знаки, не связанные структурно с другими знаками; в устной речи числа от О до 9 обозначаются отдельными словами, каждое из которых не зависит от других слов. Изучение устной нумерации чисел от 10 до 20 начинают с ознакомления учащихся с понятием Выполняя различные упражнения на счет предметов, ученики объединяют эти предметы в отдельные группы по 10 штук — пучки палочек, связки колечек и т. д. Затем вводится понятие десятка: десять предметов образуют десяток. Работу на уроке по введению чисел от 11 до 20 можно организовать так. Учитель спрашивает: «Как получить число, следующее за числом 10?. Ученики отвечают: «К 10 прибавить 1». На десять предметов — десяток — кладется еще один предмет. Сколько сейчас предметов? Получив ответ: Одиннадцать»* учитель обращает внимание на структуру этого слова: один-на-дцать, указывая, что «дцать» является сокращением слова «десять»**. Подобным образом вводятся все числа до 19. дети получают представление об образовании чисел от 11 до 19, одновременно Наконец, вводится число 20. Имея один десяток предметов и еще 9 предметов, учитель добавляет к ним один предмет, затем объединяет новые десять предметов в новый десяток и спрашивает у учащихся, сколько получилось десятков. Затем изучается десятичный состав этих чисел. Первые упражнения выполняются с использованием дидактического материала, который в дальнейшем постепенно исключается. Решаются такие типы упражнений. 1. Отсчитайте 16 предметов, отделите 10 предметов (выделите десяток). Сколько десятков в числе 16? Сколько единиц в числе 16 (сверх десяти)? Сколько всего единиц в числе 16? 2. Отсчитайте один десяток предметов, затем добавьте еще З предмета. Сколько всего предметов отсчитали? Сколько десятков и сколько единиц в числе 13? Сколько единиц в числе 13? 3. Сколько десятков и сколько единиц в числе 17? 15? 20? 4. Какое число составят 1 десяток и 8 единиц? 1 десяток и 1 единица? После усвоения учащимися устной нумерации приступают к изучению письменной Нумерации. Ознакомление учащихся с позиционным принципом записи чисел второго десятка осуществляется с помощью абака, представляющего собой таблицу с двумя рядами карманов: один из рядов предназначен для палочек, другой для цифр. В дальнейшем при изучении нумерации используют таблицу разрядов с надписями справа налево: «единицы», «десятки», а также таблицу с двумя подвижными лентами с записанными на них цифрами. Учащиеся сами изготавливают подобные пособия. Приступая к объяснению принципа записи чисел второго десятка, учитель подчеркивает, что при этом используются те же знаки, что и для обозначения чисел первого десятка цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Затем учитель называет некоторое число, например 14. Вместе с учащимися выясняется десятичный состав этого числа: 1 десяток и 4 единицы. Затем в верхний ряд карманов вставляются слева десяток палочек, связанных пучком, а справа 4 палочки, в НИЖНИЙ ряд — цифры 1 и 4. Получается обозначение числа четырнадцать. Выполняются и такие упражнения: 1) учитель на абаке обозначает число цифрами, учащиеся иллюстрируют его палочками и записывают на доске; 2) учитель на абаке обозначает число палочками, учащиеся обозначают его цифрами и записывают имя числа на доске; 3) учитель записывает число на доске. Учащиеся его читают называют число десятков и число единиц; 4) учитель называет число. Учащиеся записывают его и называют число десятков и число единиц. * Если никто из учащихся не знает названия этого что маловероятно, учитель сообщает его сам. ** В переводе с древнерусского одиннадцать означает один сверх десяти Рассматривается запись чисел 10 и 20, уясняется, что в этих записях цифра 1 (или 2) показывает, что в данном числе содержится 1 десяток (или 2 десятка), а цифра О — что эти числа не содержат единиц сверх тех, что образуют десятки. Могут быть использованы и упражнения другого характера: 1) запишите число, следующее за числом 12; 2) запишите число, предшествующее числу 20; 3) вычислите: 13+1; 13—1. При изучении нумерации чисел второго десятка учащиеся знакомятся со случаями прибавления и вычитания числа 10, прибавления к 10 и вычитания из числа всех его разрядных единиц, закрепляют свойства числа О : а + 0, а —. Например, при решении упражнения 19—9 рассуждают следующим. образом: 19 содержит 1 десяток и 9 единиц, если вычесть 9 единиц, то останется 1 десяток, т. е. 10. Особое внимание уделяется введению понятий: однозначное число», «двузначное число». Учащиеся видят, что для записи чисел, состоящих только из единиц, требуется одна цифра, а для записи чисел, состоящих из десятков или десятков и единиц,— две цифры. После этого вводятся термины: «однозначное число», «двузначное число». для закрепления введенных понятий выполняются такие упражнения: 1) записать З однозначных и З двузначных числа; 2) из множества чисел 0, 20, 11, 2, 7, 15, 10, 2, 12 выписать сначала однозначные, а затем двузначные числа. Записать их в порядке возрастания (убывания); 3) записать З однозначных числа. Увеличить каждое из них на 10. Какие числа получились? Как можно их назвать? 4) записать З двузначных числа, не равных 20. Уменьшить их на 10. Какие числа получились? Как можно их назвать? 5) с помощью цифры 1 записать однозначное и двузначное числа. Что означает цифра 1 в записи числа II? Нумерация и сравнение чисел в пределах 100. Знакомство с числами от 21 до 100 начинают с устной нумерации. Образование и называние чисел 30, 40, 50, 60, 70, 80, 90, 100 объясняется в процессе счета десятками: 1 десяток — десять единиц, 2 десятка — двадцать единиц, З десятка — тридцать единиц, 4 десятка сорок единиц, 5 десятков — пятьдесят единиц, шесть десятков шестьдесят единиц, семь десятков — семьдесят единиц, восемь десятков — восемьдесят единиц, девять десятков — девяносто единиц, десять десятков — сто единиц. При введении и анализе названий десятков обращается внимание на то, что все они, кроме «сорок» и «сто», образованы по одному принципу. Правда, слово «десять» претерпело разные изменения в группе «двадцать-тридцать» и в группе «пятьдесят- шестьдесят-семьдесят-восемьдесят». На ранних ступенях развития русского языка вместо «сорок» и «сто» говорили «четыредесять» и «девятьдесять». Поясняя происхождение слова «сорок», полезно сов ершить экскурс в историю*. * Тридцать образовалось как и двадцать ‘пятьдесят образовано в результате сращения спять десять — пять десятков; подобным образом образовались шестьдесят*, семьдесят, восемьдесят девяносто встречается в памятниках 84

Освоив счет десятками, учащиеся знакомятся с образованием итенами Любых чисел в пределах сотни: 2 десятка и 5 единиц — это двадцать пять; 4 Десятка и 7 единиц — это сорок семь и т. п. Упражнения на образование чисел чередуются с упражнениями на разложение чисел: пятьдесят шесть — это 5 десятков и шесть единиц; Девяносто один это 9 десятков и 1 единица и т. п. При изучении письменной нумерации учащиеся знакомятся с понятиями разряда и разрядного числа. Поясняется, что, например, тридцать семь — это З десятка и 7 единиц, но можно сказать и по- Другому: З единицы второго разряда и 7 единиц первого разряда. Здесь полезно использовать карточки с разрядными числами, которые Помогают Усвоить состав числа, представить его в виде суммы разрядных слагаемых (56=50+6). Эти навыки затем используются при изучении Операций над натуральными числами. Изучая нумерацию в пределах 100, учащиеся выполняют упражнения на сложение и вычитание: 1) прибавление и вычитание числа 1; 2) прибавление к целому числу десятков однозначного числа; З) вычитание всех десятков из числа; 4) прибавление целого числа десятков к однозначному числу; 5) вычитаНие всех единиц из числа. Методика вычислений здесь та же, что и для Подобных случаев в пределах 20. При выполнении упражнений на присчитывании и отсчитывании единицы, чисел, кратных 10, используется наглядное пособие «лента ста» --— метровая лента с обозначенными сантиметрами и дециметрами Усвоению Последовательности чисел первой сотни в натуральном ряду способствуют также следующие упражнения: 1) назовите число, предшествующее Числу 27 (после какого числа при счете Называют число 27?) 2) Назовите Число следующее за числом 27 (перед каким числом при счете называют число 28?); З) между какими Числами называют при счете число 27? - Работа по усвоению нумерации продолжается и при изучении операций сложения и вычитания в пределах 100. Итак, изучив нумерацию чисел в пределах 100, учащиеся должны усвоить: а) имена двузначных чисел в устной и Письменной речи, их десятичный состав; б) расположение чисел до 100 ‘в натуральном ряду; в) смысл терминов: «единица первого разряда», «единица второго разряда», «разрядное число», «Однозначное число», «Двузначное число». Сложение и вычитание. При изучении Операций сложения и вы- с ХiУ в. как вытеснившее общеславянское «девять-десять» которое сохранилось в других славянских языках, кроме восточнославянских, происхождение «девяносто» неясно; «сто» является общеславянских словом индоевропейского характера; «сорок» используется в восточнославянских языках, пришло на Смену «четыре Десять», возникло на базе Слова «сорок» — «мешок, рубаха» из-за обычая продавать соболиные шкурки сороками с 40 шкурками; таким образом, «сорок» — сначала «мешок», затем «мешок с сорока соболиными шкурками» и, наконец, «сорок) — обозначение четырех десятков.

Вычитания в концентре «десяток» учащиеся должны усвоить главным образом таблицы сложения и вычитания в пределах десяти, В концентре «Сотня» ученики должны овладеть приемами устных вычислений. Эти приемы в дальнейшем используются при устном сложении и вычитании в пределах тысячи, миллиона.

Целесообразность методики обучения вычислительным приемам можно оценить по следующим характеристикам: 1) приемы должны допускать иллюстрацию с помощью наглядных пособий; 2) количество приемов сложения и вычитания в пределах ста должно быть минимальным, а необходимость изучения того или иного приема

методически обоснованной.

Рассмотрим методику обучения учащихся приемам устного сложения и вычитания, удовлетворяющую этим характеристикам.

Выбор вычислительных приемов в начальной школе в значительной мере определяется возможностями наглядной иллюстрации их сущности. Основным наглядным пособием при изучении чисел от 10 до 100 является абак. Удобен абак следующей конструкции: наборное полотно с горизонтальными «карманами», в которые укладываются одинаковые по размеру вырезанные из картона квадраты (единицы) или полоски, состоящие из 10 квадратов (десятки). В каждом кармане можно разместить не более 10 квадратов (одну полоску).

Иллюстрация вычислительных приемов с помощью абака предполагает наличие у учащихся некоторого опыта работы с этим наглядным пособием. Абак может использоваться уже в концентре «десяток», а также в дальнейшем, когда изучаются темы, связанные с нумерацией, арифметическими операциями и сравнением чисел. К началу обучения работе с абаком учащиеся должны уметь устанавливать взаимно однозначное соответствие между элементами двух множеств. Например, откладывать столько кружков, сколько яблок изображено на рис. 13.

Навыки работы с абаком могут отрабатываться при выполнении учащимися, например, следующих систем упражнений.

Первая серия упражнений

Усл о в и е. Учащимся показывают иллюстрации, на которых изображено не более 10 предметов.

Т р е бует с я: изобразить на наборном полотне, сколько всего предметов; сколько предметов останется, если несколько предметов убрать.

Работа над заданиями:

1) учащиеся отбирают столько квадратов, сколько предметов изображено на иллюстрации;

2) отобранные квадраты правильно укладываются в карман наборного полотна: карман заполняется справа налево, квадраты плотно соприкасаются боковыми сторонами. На рис. 14, а квадраты уложены правильно, на рис. i4, б — неправильно;

3) из кармана справа убирают столько квадратов подряд, сколько убрали предметов. На рис. 15, а квадраты убраны правильно, на рис. 15, 6 — неправильно.

Вторая серия упражнений

Усл о в не. Учащимся предъявляется больше 10, но меньше 20 предметов. Т р е бует с я: правильно показать на наборном полотне, сколько всего предметов; сколько предметов останется, если несколько предметов убрать.

Работа над заданием:

i) отбирается столько квадратов, сколько предметов предъявлено;

2) когда отобрано квадратов, в наборное полотно укладывается полоска;

3) остальные квадраты устанавливаются в следующем кармане по уже известному из первой серии упражнений правилу;

(Пусть для определенности было всего 13 предметов, 6, из них убрали.)

4) убираются З квадрата из наборного полотна;

5) чтобы убрать З оставшихся квадрата, полоску в наборном полотне заменяют квадратами и по известному правилу убирают З квадрата.

Третья серия упражнений

У с л о в и е. Демонстрируются рисунки с двумя (тремя, четырьмя) группами предметов разного вида, но одного рода (в совокупности не более 10), например 2 мяча, 1 матрешка и 4 игрушечных автомобиля.

Т р е бует с я: правильно изобразить на наборном полотне, сколько всего игрушек.

Работа над заданием:

1) в карман правильно укладываются квадраты, соответствующие количеству мячей;

2) правильно укладываются квадраты, соответствующие количеству матрешек:

квадраты укладываются в тот же карман, слева направо, начиная от последнего уложенного;

3) правильно кладутся квадраты, соответствующие количеству автомобилей. На рис. 16, а квадраты уложены правильно, на рис. 16, 6 — неправильно.

Четвертая серия упражнений

Усл о в и е. Школьникам предъявляются предметы разного вида (не более 10 каждого), но одного рода, причем в совокупности их более 10.

Т р еб у е т с я: изобразить на наборном полотне, сколько всего предметов. Работа над заданием (предметы трех видов представлены в следующих количествах—5, 7,9):

i) правильно укладываются 5 квадратов, соответствующих количеству предметов первого вида;

2) правильно располагают квадраты, соответствующие количеству предметов второго вида (по правилу, отработанному во второй серии упражнений);

3) по правилам, использовавшимся во второй и третьей сериях упражнений, укладываются квадраты, соответствующие количеству предметов третьего вида. На рис. 17 изображен правильно заполненный абак.

Рассмотренные упражнения (или некоторые из них) могут выполняться как дидактические игры. Учащиеся должны усвоить правила укладки квадратов в карманы абака и удаления их из карманов, замены квадратов полосками и полосок квадратами.

Сложение. для того чтобы выработать подход к изучению определенного учебного материала, в методике используют логикодидактический анализ. Воспользуемся им для определения целесообразной последовательности изучения приемов устного сложения чисел в пределах ста.

Рассмотрим все возможные случаи сумм в зависимости от разрядного состава входящих в них слагаемых: это суммы, у которых значения больше 10 (суммы, равные 10, изучались в концентре «десяток») и не больше 100.

К первой группе можно отнести суммы однозначных слагаемых:

2+9, 3+8 и т. п.

Вторую группу составляют суммы, в которых одно слагаемое двузначное, а другое однозначное: 20+5, 22+5, 28+5 и т. д. Эта группа не является однородной. Найти сумму 22+5 сложнее, чем 20+ 5. Случай же 28+5 (с образованием нового десятка) самый ложный в данной группе.

В третью группу входят суммы двузначных слагаемых. Очевидно, что и эта группа по уровню сложности входящих в нее сумм разделяется на подгруппы. Сложение круглых десятков интуитивно можно оценить как самый простой случай. Сложнее найти сумму, когда одно двузначное слагаемое оканчивается нулем, а второе имеет ненулевой разряд единиц (20+35, 28+40 и т. п.). Затем следуют суммы, у которых оба слагаемых не заканчиваются нулем, но при сложении не образуется дополнительный десяток (25 +34, 48+ 51 и т. п.), и, наконец, суммы, в которых при сложении образуется новый десяток (25+37, 38+56 и т. п.).

Суммы вида 25+5 и 42+28 отнесем соответственно ко второй и третьей группам.

для наглядности рассмотренные виды сумм представлены в табл. 2, где они расположены в порядке возрастания сложности.

Уровни сложности а—ч! определены интуитивно. для того чтобы расположить все 8 случаев сложения в порядке Возрастающей трудности, интуиции недостаточно. В самом деле, опираясь только на интуицию, нельзя определённо сказать, чтоб вычислить проще: 22+5 или 20+35; 9+5 или 22+35. А между тем этот вопрос имеет принципиальное значение: в соответствии с дидактическим принципом «от простого к сложному» приемы вычисления должны изучаться по Возрастающей сложности.

Кроме того, поскольку учащиеся должны научиться складывать числа в пределах 100 в уме, то ясно, что большое количество приемов сложения делало бы эту задачу трудно выполнимой. Поэтому желательно уменьшить число таких приемов, обобщив их.

Исходя из особенностей абака как средства интерпретации, определим вычислительные приемы для случаев (1)—(8).

(1)

Приведем примерный диалог между учителем и учеником при работе с абаком над приемом вычисления этой суммы.

У ч и т ел ь: В кармане наборного полотна 9 квадратов. Можно ли в этот карман положить квадраты, соответствующие второму слагаемому?

У ч е н и к: Нет, В этот карман можно положить только один квадрат.

Уч и т ел в: Сколько квадратов еще останется положить?

Ученик: 4 квадрата.

Учитель: Как ты это определил?

У ч е н и к: 5 — это 4 и 1. Один положить можно к 9, значит, останется положить еще 4.

У ч и т е л ь: Заполни наборное полотно и говори вслух, как ты это делаешь.

У ч е н и к: 1 квадрат поместим к 9 квадратам. Получится 10 квадратов. Заменим их полоской, 4 квадрата поместим в другой карман.

Выполняются соответствующие математические записи: 9+ (1 + +4) — выясняется, сколько квадратов из 5 можно добавить в карман с первым слагаемым и сколько квадратов останется; (9+1)+ +4—заполняется карман с первым слагаемым; 10+4 — квадраты в этом кармане заменяются полоской («десятком)>) и 4 квадрата укладываются в другой карман абака. Сумма 10+4 находится по «определению» чисел второго десятка.

(2)20+5.

При знакомстве с нумерацией двузначных чисел учащиеся учились называть числа, состоящие из нескольких десятков и нескольких единиц: 20+5 это 2 десятка и 5 единиц, т. е. 25.

(3) 22+5.

Учащиеся знают, как показать на абаке первое слагаемое. По правилу работы с абаком 5 квадратов (второе слагаемое) укладывается в кармашек с двумя единицами первого слагаемого. Математически это описывается так: (20+2) +5=20+ (2+5). для разложения числа 22 на разрядные слагаемые используется правило называния двузначных чисел или вычислительный прием (2). Этот прием используется для получения ответа: 20+7=27.

(4)28+5.

Первое слагаемое представляется на абаке двумя полосками и

8 отдельными квадратами. Второе слагаемое — квадратами. Значит,

согласно правилу работы с абаком, второе слагаемое прибавляется

к 8. Таким образом:

(20+8) +5— прием (2);

20-(.5) —прием (1);

20+ 13 прием нахождения значения суммы такого вида еще не рассматривался. Он будет изучаться после приема (6): сложение двузначных слагаемых, одно из которых круглые десятки. Значит, случай сложения (4) должен изучаться после случая (6)

(5) 20+30.

Абак заполняется сначала двумя полосками, а затем в него кладут еще З полоски. Всего в абаке 2+3 полоски, или 5 десятков. Таким образом, прием сложения круглых десятков состоит в подсчете десятков: 2 десятка + З десятка = 5 десятков, т. е. в сложении однозначных именованных чисел.

(6) 20+35.

В соответствии с приемом (2) число 35 можно представить в виде суммы 30+5. К двум пол9скам (первому слагаемому), находящимся в абаке, укладываются еще З полоски второго слагаемого, а затем в отдельный карман еще 5 квадратов второго слагаемого:

20+ (30+5) = (20+30) +5.

Сумма круглых десятков определяется с помощью приема (5); сумма 50+5—прием (2).

(7) 22+35.

Как и в предыдущем случае, второе слагаемое помещается в абак по частям — отдельно десятки и отдельно единицы:

22+(30-I-5) -1-прием (2);

(22+30) +5 прием (6);

52 + 5 = 57 (прием (3).

(8) 25+36.

Аналогично приемам (6) и (7) второе слагаемое в этой сумме укладывается в абак разрядными единицами — десятками и единицами:

25+(ЗОЧ-6) —прием (2);

(25+30) +6 прием (6);

55+6= 61 —прием (4).

Итак, определены приемы сложения чисел в пределах ста и выявлены связи между этими приемами. Схематически эти связи изображены на рис. 18.

Из схемы видно, что основными являются приемы (1), (2), (5). Остальные 5 представляют собой их комбинации. Таким образом, число вычислительных приемов минимизировано. Теперь определим последовательность изучения различных случаев сложения в пределах 100. Эта задача решена лишь отчасти. Из рис. 18 видно, что 8 выделенных случаев сложения упорядочены частично. Так, например, суммы вида 22 +35 (7) нужно рассматривать после изучения приемов вычисления сумм вида 20+5 (2), 22+5 (3), 20+35 (6). Однако схема не содержит информации о том, какой случай сложения следует изучать раньше— (7) или (1)? (7) или (8)? (7) или (4)?

Таким образом, равно возможны различные варианты последовательности их изучения: (1, 2, 5, 3, 6, 7, 4, 8), (2, 3, 5, 6, 7, 1,4, 8), (1, 2, 3, 5, 6, 4, 8, 7), (5, 2, 6, 1, 4, 8, 3, 7) и т. д.

С дидактической (методической) же точки зрения эти варианты не

равнозначны.

Очевидно, что изучение операции сложения (вычитания) не может происходить в отрыве от усвоения учащимися нумерации натуральных чисел. (Вспомним, что знакомство с числа ми первого десятка происходило одновременно с изучением операций сложения и вычитания: каждое новое число появлялось в результате прибавления к предыдущему числу единицы.) Как известно, нумерация двузначных чисел вводится в следующем порядке: усваиваются названия

и запись чисел второго десятка

(от 11 до 19), затем круглые десятки

и, наконец, остальные двузначные

числа. -2Зб--4’i..

При сложении однозначных чисел с переходом через десяток (суммы вида (1)) получаются числа второго десятка. Естественно, что суммы вида 9+2, 4+7 должны рассматриваться параллельно с изучением нумерации чисел от 11 до 19. Таким образом была бы достигнута преемственность в изучении таблицы сложения: числа от О до 10 учащиеся узнают одновременно с табличными случаями сложения в пределах 10; знакомство с числами следующего десятка связано с изучением остальных случаев табличного сложения. Причем при использовании приема (1) интенсивно «работает» таблица сложения в пределах 10.

При изучении нумерации круглых десятков используется понятие «десяток». Слова «двадцать», «тридцать» и другие служат названиями двух десятков, трех десятков и т. д. Поэтому естественно ввести прием сложения круглых десятков, в котором понятие «десяток» выполняет важную функцию: 10+20 заменяется суммой: 1 десяток+2 десятка=3 десятка, откуда 10+20=30.

Знакомство с остальными числами в пределах 100 предполагает использование понятия разрядных слагаемых: 21 — это два десятка и одна единица, или 20 + 1. Таким образом, изучение приема (2) происходит в неразрывной связи с изучением нумерации двузначных чисел с ненулевыми разрядами единиц.

Известно, что при усвоении разрядного состава чисел учащиеся часто путают разряды десятков и единиц. Поэтому методически целесообразно рассматривать случаи сложения вида 25 + 3 (3) и 25 + +30 (6) непосредственно после введения нумерации двузначных чисел в пределах 100. Причем больший эффект достигался бы при одновременном изучении обоих приемов, так как при этом можно противопоставить не только внешний вид сумм 25+3 и 25+30, но и их значения — 28 и

достаточно трудно убедительно обосновать целесообразность той или иной последовательности изучения остальных приемов, поэтому будем полагаться на интуицию: сначала изучается прием (4), затем (7) и, наконец, (8).

Итак, логико-дидактический анализ темы «Сложение в пределах 100» позволил определить методически целесообразный порядок изучения всевозможных случаев сложения чисел из множества (10, 11,

100}:

9 + 5—э.-20 + 30—.20+5-22 + 3—-28 + 6-*22 + 35—25+36.

22 + 30

(1) (5) (2) (3) и (6) (4) (7) (8)

При изучении приемов устного сложения учащиеся знакомятся с ассоциативным законом сложения. В начальной школе этот закон раскрывается с помощью правил прибавления числа к сумме и суммы к числу.

‚ В § 10 рассматривалась методика знакомства учащихся со скобками в числовых выражениях. Поэтому сразу перейдем к раскрытию содержания методики обучения учащихся названным правилам.

Учитель должен убедить учащихся, что для вычисления значений выражений (а + Ь) + с и а + (Ь + с) действия можно производить в любом порядке, т. е. значение выражений не зависит от порядка выполнения действий. Усвоение учащимися этих правил не вызывает трудностей, если их математическое содержание будет раскрываться с опорой на интуитивные представления детей, их житейский опыт. Учитывая это, в начале изучения, например, правила вычисления суммы (а + Ь) + с учащимся предлагают серию задач, имеющих разный сюжет, но одинаковое математическое содержание, например:

«Мальчик нашел два белых гриба, три подосиновика и четыре подберезовика. Сколько всего грибов нашел мальчик?»; «В вазу положили два яблока, пять слив и три груши. Сколько всего фруктов в вазе?»

Работа над этими задачами ведется по следующему плану. Условие первой задачи конкретизируется: «Мальчик сначала нашел два белых гриба...» На наборном полотне появляется соответствующая иллюстрация. «...Затем три подосиновика...» Иллюстрация на наборном полотне дополняется. «...А потом под березой он нашел еще четыре подберезовика». Учитель устанавливает на наборном полотне еще четыре «гриба». «Сколько всего грибов нашел мальчик?» Выполняется запись: (2 + 3) + 4.

Учащиеся могут заполнить индивидуальные наборные полотна, используя вместо «грибов» геометрические фигуры разного цвета.

Затем читается другой вариант этой же задачи: «Мальчик сначала нашел три подосиновика, потом под березой — четыре подберезовика. После этого ему посчастливилось найти еще два белых гриба». В соответствии с текстом задачи заполняется следующий карман наборного полотна (рис. 19). Составляется соответствующая математическая запись: +4) +2.

Аналогичным образом условие задачи перефразируется. в соот

ветствии с выражением (4+2) +3. Заполняется еще один карман наборного полотна (рис. 19).

В заключение делается вывод, что исходную задачу можно решить разными способами (2+3) +4= (3+4) +2. Интуиции детей достаточно для того, чтобы они увидели справедливость данных равенств, не прибегая к вычислениям.

для второй задачи учитель пишет рядом с карманами еще незаполненного наборного полотна по одному выражению: (2 +5) + +3, (2+3) +5, (5+3) +2. Сюжеты к этим выражениям по данной задаче предлагается составить самим учащимся.

Наконец, школьникам можно предложить составить задачу по числовому выражению вида (а + Ь) + с и перефразировать ее условие так, чтобы она решалась с помощью выражений (а + с) + Ь и (Ь+с)+а.

В заключение формулируется правило: прибавить число к сумме можно, складывая числа в любом порядке. Запоминание учащимися более детальной формулировки («чтобы прибавить число к сумме, можно сначала найти значение суммы, а потом прибавить число; можно к первому слагаемому суммы прибавить число, а потом прибавить второе слагаемое суммы...» и т. д.) нецелесообразно. Такие формулировки создают опасность формального усвоения сути правила. Гораздо важнее выработать у учащихся привычку обращаться к задачам, если правило ими забыто.

Правило закрепляется в процессе решения соответствующих числовых примеров. Например: «Запиши удобный способ вычисления значения данных выражений: (8+2) +5; (7+5) +3; (6+5) +5» и т. д. Так как учащиеся еще не изучали прием сложения однозначных чисел с переходом через десяток, последовательность вычислений определяется однозначно.

В ы ч и т а н и е. Выполним логико-дидактический анализ вычитания в пределах 100. Основным наглядным пособием при изучении вычитания также является абак.

Выделим всевозможные виды разностей чисел в пределах 100 (табл. 3).

На основе логико-дидактического анализа темы сложения можно

сразу выделить основные случаи вычитания: 45 — 5, 45 — 40,

— 20.

(1) 40—20.

Этот прием естественно формировать у учащихся одновременно

приемом сложения круглых десятков. Разность 40—30 рассматривается как разность однозначных именовннь1х чисел: 4 дес. — З дес.= 1 дес., т. е. 40—30= 10.

(2) 45 —5 и 45—40.

Эти приемы рассматриваются при знакомстве учащихся с нумерацией двузначных чисел типа 21, 22, 23 и т. д. Они, так же как и при-

сложения для сумм вида 40+5, основываются на знании учащихся разрядного Состава двузначных чисел. Этим обусловлена воз)ЖНОСТЬ одновременного изучения данных приемов сложения и 1читания. Приемы (1) и (2) не требуют средств наглядности.

Раскроем содержание приемов, которые иллюстрируются с помощью абака.

(3) 45—З.

На абаке изображено уменьшаемое 45. Число З вычитается из числа единиц уменьшаемого

(4О+5)_З_ прием (2);

4О+(5_З)40+2прием (2)

(4) 40—5.

На а не изображено уменьшаемое. Согласно правилу работы с абаком, 1 из 4 полосок заменяется 10 квадратами и 5 из них удаляются. Математически это записывается так:

______ —прием (1);

=ЗО+(IО_5)=30+5прием (2).

(5) 45—9.

В абаке находятся 4 ПОЛОСКИ и 5 квадратов. Сначала из него играют 5 квадратов. Остальные 4 квадрата удаляются так же, как в случае 40—5:

— прием (2); =40-_-436 —прием (4).

(6)

На абаке изображено уменьшаемое 45. Очевидно, что нужно удалить З ПОЛОСКИ. Это выражается следующей записью:

(40+5)—30 —прием (2);

(40—З0)+5 —приём (1

=10+5—_прием (2).

(7)

Числу 45 в абаке соответствуют 4 полоски и 5 квадратов, а числу 23—2 полоски и З квадрата. Поэтому из абака удаляются 2 полоски и З квадрата:

45—(20+З)= —прием (2);

=(4)_-3== —прием (б);

=(25—3)— прием (3).

(8) 45—28.

В абаке находятся 4 полоски и 5 квадратов. Исходя из разрядного состава вычитаемого, удаляют 2 полоски и 8 квадратов. Математически это записывается так:

45—(20+8)= —прием (2);

=(45—20)----8= —прием (б);

=25—8—прием (5).

Теперь можно построить схему, отражающую связи между рассмотренными приемами (рис. 20). Схема позволяет определить разные варианты порядка изучения

приемов вычитания. Выше было установлено, что целесообразно рассмотреть с учащимися сначала прием (1), а затем прием (2), причем в связи с соответствующими приемами сложения.

Методически целесообразно также изучать приемы вычитания (3) и (б) одновременно с нумерацией двузначных чисел вида 21, 22, 23... Это позволит закрепить знания учащихся о позиционном значении цифр в двузначном числе.

Труднее обосновать порядок изучения приемов (4), (5), (7) и (8). Возможны варианты — (4, 5, 7, 8), (7, 4, 5, 8), (4, 5, 8, 7). Остановимся на такой последовательности: (4)—(5)-----(7)—(8).

Итак, с помощью логико-дидактического анализа обоснован следующий порядок изучения сложения и вычитания в связи с изучением нумерации чисел в пределах 100:

В приемах вычитания используются правила вычитания числа из суммы (см. приемы (3), (4), (6)) и вычитания суммы из числа (см. приемы (5), (7), (8)). Они изучаются по такому же плану, что и правила прибавления числа к сумме и суммы к числу. 1. На уроке рассматривается текстовая задача, математическое содержание которой описывается выражением вида (а + Ь) — с (где а и Ь больше с) или т — (п + р). Затем условие этой задачи изменяется в соответствии с выражениями (а — с) + Ь и (Ь — с) + а или (т—п)—р и (т—р)----п. Например, для обоснования правила вычитания числа из суммы может быть предложена такая задача: «У мальчика было 8 синих и б красных воздушных шаров. Он отдал сестре 4 шара. Сколько шаров осталось у мальчика?» Выясняется, что задаче соответствует выражение (8+6) —4. Если условие этой задачи конкретизировать «У мальчика было 8 синих и б красных воздушных шаров. Он отдал сестре 4 синих шара. Сколько шаров осталось у мальчика?» или «У мальчика было 8 синих и б красных воздушных шаров. Он отдал сестре 4 красных шара. Сколько шаров осталось у мальчика?», то исходное выражение принимает следующий вид: (8 — 4) + б или (6 — 4) + 8. С помощью иллюстрации на наборном полотне легко показать, что ответ не изменяется, т. е. (8+6) —4= (8—4) +6= (6—4) +8. 2. Учащимся предлагаются числовые выражения вида (а + Ь) — с, (а—с)+Ь, (Ь—с)+а или т—(п+р), (аг—п)---р, (т—р)—п, по которым необходимо составить три задачи, имеющие похожий сюжет и одинаковые числовые данные. Цель этой работы состоит в том, чтобы, с одной стороны, показать учащимся реальный характер отношений (а + Ь) — с = (а —— с) + Ь = и iп—(п+р)_—(,ч-—п)—р=(т—р)—а. С другой стороны, школьники должны увидеть, что данные правила можно «вспомнить», если составить, а затем переформулировать условие задачи. Последнее особенно важно, если иметь в виду опасность заучивания этих правил учащимися. 3. Наконец, правило отрабатывается на системе целесообразных упражнений. Рассмотрим методику обучения учащихся вычислительным приемам в пределах 100. Изучение каждого приема осуществляется по следующему плану. На демонстрационном абаке выполняются действия, раскрывающие суть приема. Под руководством учителя учащиеся дают пояснения действиям с абаком, которые позволяют сформулировать их на математическом языке — записать на доске в виде числовых выражений. Рассматривается аналогичная сумма (разность). Учитель на демонстрационном абаке, а учащиеся на индивидуальных абаках одновременно выполняют преобразования. Математические выражения записываются на доске и в тетрадях. дальнейшая работа над вычислительным приемом проводится без абака, с полной или сокращенной записью промежуточных действий в тетрадях, с проговариванием этих действий вслух или про себя. При этом учащиеся Пользуются Соответствующей терминологии «разложу уменьшаемое на разрядные (удобные) Слагаемые>, «вычту ЧИСЛО из суммы>, «прибавлю ЧИСЛО к сумме> и т. п. Приведем ВОЗМОЖНЫЙ диалог учителя с учеником при Изучении приема Вычитания однозначного числа ИЗ круглых десятков. На доске Записано число 30. Учите л Ь: Как Изобразить ЧИСЛО ЗО на наборном Полотне? Учен и к: В З Кармашка нужно ПОЛОЖИТЬ ПОЛОСКИ, Обозначающие десятки. Уч и т ел ь: Из числа ЗО нужно вычесть 4. Как изобразить на наборном Полотне, что вычитается 4? Уч е н и к: Вычесть 4 единицы — это значит убрать 4 Квадрата. Уч и т ел ь: Но ведь в кармашках Содержатся ТОЛЬКО ПОЛОСКИ. Уче н и к: Каждую Полоску МОЖНО заменить 1О Квадратами. Уч и т ел ь: Нужно ли все ПОЛОСКИ заменять квадратами? Быстро с такой задачей не справиться... Учен и к: Убирается всего 4 квадрата, значит, достаточно заменить Квадратами ТОЛЬКО Одну полоску. Все эти операции ВЫПОЛНЯЮТСЯ на демонстрационном абаке и после того, как убраны 4 квадрата, подсчитывается ответ. Учащиеся проговаривают выполняемые действия, учитель с помощью учащихся выполняет на доске соответствующие записи. В Заключение сделаем два Замечания 1. Изучая приемы устного сложения двузначных чисел, учащиеся должны прийти к выводу, что СЛОЖИТЬ два двузначных Числа легче, если к десяткам первого прибавить число Десятков Второго, единицы обоих слагаемых сложить и прибавить к сумме Десятков. для того чтобы этот прием был эффективен, учащиеся должны хорошо знать таблицу сложения. 2. Кроме рассмотренных ОСНОВНЫХ Приемов, полезно показать учащимся некоторые частные приемы, Основанные на связи между компонентами и результатами операций. Пусть, например, складываются числа 39 и 46. Замечают, что 39— это 40 без одного. К 40 прибавить 46 легко, получается 86. Но одно из слагаемых было увеличено на единицу, поэтому Сумму нужно на единицу уменьшить: 86 1 85. Аналогично поступают, если, например, к 58 прибавляется 37. К первому слагаемому добавляют 2 единицы, а от полученной суммы 97 вычитают 2. Более сложные рассуждения используются для объяснения аналогичных приемов вычитания, например 65—39: «Вычитаемое увеличиваем на единицу: 65—40. Но от этого разность уменьшается на единицу, поэтому к 25 нужно прибавить 1з. Умножение и деление. Усвоение учащимися нумерации чисел в пределах 1оо открывает возможности для обучения их табличному умножению и делению. Изучение операций умножения и деления в концентре «Сотня» предполагает усвоение учащимися таблицы умножения однозначных чисел и соответствующих случаев деления. Кроме того, ученики должны усвоить приемы устного Умножения и деления в случаях, не являющихся табличными. Табличное умножение и деление. Изучение этой темы осуществляет по следующему плану: 1) раскрывается СМЫСЛ операций умножения и деления;

2) учащиеся усваивают особые Случаи умножения и деления (единицы и нуля, на единицу и нуль).

3) изучаются таблицы умножения чисел 2, 3, 4, 5, 6, 7, 8, 9 на однозначные числа и соответствующие случаи деления.

Из вузовского курса математики известны два подхода к определению произведения натуральных чисел — через декартово произведение множеств и аксиоматическое (определение через сложение). В начальной школе ни один из этих подходов невозможно осуществить в полном объеме. Однако возможно использование их некоторых элементов. Так, умножение в начальных классах определяется через сложение (деление — через умножение). Главным же средством наглядности при изучении умножения является таблица, иллюстрирующая декартово произведение двух множеств.

Как и все основные математические понятия в начальной школе,

умножение и деление вводятся с помощью системы целесообразных задач с последующей математизацией их содержания.

При знакомстве с операцией умножения учащимся могут быть предложены, например, следующие задачи.

Задача 1. Автомобиль «Волга может одновременно перевезти 4 пассажиров. Сколько людей смогут перевезти за одну поездку З автомобиля «Волгах.?

Задача 2. Ученик купил 5 тетрадей и заплатил за каждую 2 к. Сколько всего денег заплатил ученик?

Задача З. Масса 1 пакета картофеля —З кг. Хозяйка купила З таких пакета. Сколько килограммов картофеля она купила?

Особенность таких задач состоит в том, что учащиеся могут легко обнаружить в условии одинаковые слагаемые. Встречающиеся в них величины должны быть хорошо знакомы учащимся и допускать наглядную иллюстрацию.

Формулируется задание: записать выражения к задачам. Уже при изучении таблицы сложения учащиеся встречались с суммами, имеющими более двух слагаемых, два или более одинаковых слагаемых. Поэтому данное задание не должно вызывать у них затруднений.

Записан соответствующие выражения (4+4+4, 2+2+2+2+ +2, 3+3+3), учитель сообщает учащимся, что эти суммы можно записать иначе с помощью умножения: 4 3, 2 5, 3• 3. Первый множитель показывает, чему равно каждое слагаемое в сумме, а второй — сколько слагаемых в сумме. Точка обозначает действие

умножение. Выражение вида 4 3 называется произведением. Таким образом, решение приведенных выше задач можно записать в виде

СУММЫ и произведения.

Целесообразно предложить учащимся самим придумать задачи, решаемые умножением, либо составить задачи по данным выражениям: 5+5+5+5 и 5.4, 7+7 и 7.2, 14+14+14+14 и 14.4 ит.д.

При работе над задачами выполняются различного рода иллюстрации. Например, может бы?ъ использована прямоугольная табли

ца, которая позволяет наглядно представить декартово произведение двух множеств. Таблицу (рис. 21) можно сделать из фанеры. Ряды и столбцы таблицы нумеруются. Размеры «окон определяются с таким расчетом, чтобы в них можно было закрепить рисунки. Задача может быть решена умножением, если заполненная часть таблицы имеет вид прямоугольника. Так, например, рис. 22 иллюстрирует задачи 1 и 2.

После содержательных задач учащимся предлагаются числовые выражения суммы, которые необходимо представить в виде произведения. Так как учащиеся при вычислении произведений пользуются сложением, слагаемые в этих суммах могут быть и двузначными: 30+30+30, 25+25+25+25 и т. д.

Выполняются также задания другого рода: «Представить в виде суммы следующие произведения: 2.4, 15 .3, 4 2» и т. д.

Тема «деление» в методическом отношении более сложная, чем «Умножение И это естественно: вводи операцию умножения, учитель опирается на хорошо усвоенную учащимися операцию сложения, на отработанные вычислительные навыки. деление же нельзя определить через умножение, поскольку и умножение является для учащихся новой операцией. Таким образом, роль содержательных задач, наглядных пособий при введении деления еще более значительна, чем при умножении.

Методика обучения решению таких задач будет раскрыта в § 20. Сейчас же покажем возможности использования демонстрационной таблицы для раскрытия смысла деления.

Рассмотрим, например, следующие задачи.

Задача 4. для одновременной перевозки 12 человек выделено несколько автомобилей «Волга». Одна «Волга» может взять 4 пассажиров. Сколько автомобилей было выделено для перевозки?

Задача 5. Ученик купил 5 одинаковых тетрадей и заплатил 10 к. Сколько стоит одна тетрадь?

Задача б. Масса 1 пакета картофеля составляет З кг. Хозяйка купила 9 кг картофеля. Сколько пакетов она купила?

Решаются эти задачи с использованием наглядных пособий. Так, 12 кружков, которые соответствуют количеству пассажиров из 4, раскладываются группами по 4, а затем подсчитывается количество групп; 10 квадратов (задача 5) раскладываются по 5 и подсчитывается, сколько групп квадратов получилось, и т. д.

Этими же геометрическими фигурами заполняется демонстрационная таблица. Например, 12 отобранных для задачи 4 кружков располагаются в строках таблицы: в первой строке — 4 кружка (количество пассажиров в первой машине); во второй — 4 и т. д. Обращается

внимание учащихся на то, что в таблице заполнен прямоугольный участок (рис. 23).

Учитель сообщает, что, решая задачу 4, число 12 разделили на 4 и получили в результате число З. деление 12 на 4 записывается так: 12:4. Число 12 называется делимым, 4 — делителем, З - частным.

Сравниваются условия задач 1—З и 4—6. Похожи не только они, схожи и иллюстрации, выполненные с помощью демонстрационной таблицы. Анализ этого сходства позволяет учащимся осознать связь между умножением и делением: если произведение разделить на один из множителей, то получится второй множитель. На практике это может быть достигнуто следующим образом.

Учащимся предлагается задача: К празднику Октября родители купили сыну 4 воздушных шарика. Каждый шарик стоит З к. Сколько денег заплатили родители за шарики? Кратко записывается условие задачи:

Купили — 4 шарика.

Цена — З к.

Заплатили —? к.

Составляется выражение: 3. 4= 12.

Затем предлагается другая краткая запись:

Купили —? шариков.

Цена — З к.

Заплатили — 12 к.

Выясняется, чем вторая задача отличается от первой. Вторая задача называется обратной первой. Записывается ее решение:

12:3=4.

Рассматривается краткая запись еще одной задачи, обратной первой:

Купили — 4 шарика.

Цена — ? к.

Заплатили — 12 к.

Записывается решение: 12:4=3.

делается вывод: 3. 4=12, значит, 12:З=4 и 12:4= 3.

Чтобы подготовить учащихся к изучению таблицы умножения и соответствующих случаев деления, необходимо ознакомить их с переместительным законом умножения и особыми случаями умножения и деления. для этого целесообразно воспользоваться демонстрационной таблицей. Иллюстрируем на ней произведения З . 4 и 4 3

(рис. 24), 2 . 5 и 5 2, легко убедить учащихся, что эти произведения равны — очевидно равенство соответствующих прямоугольников. Здесь же нужно показать, что наученное свойство можно использовать при вычислении значений произведений. Например, до знакомства с этим свойством при вычислении произведения 2. 9 необходимо было подсчитать значение суммы, состоящей из 9 слагаемых. Переместительный закон позволяет упростить вычисления: 2. 9

9. 2, а 9. 2=9+9. Работа над упражнениями такого рода

является хорошей подготовкой к изучению

таблицы умножения.

г Усвоение учащимися переместительного закона умножения позволяет несколько изменить требования к решению задач с помощью умножения.

до изучения этого закона задача 2, например, решалась с помощью выражения 2.5(2 к.. 5=10 к). Выражение 5 . 2 казалось необъяснимым исходя из условия задачи (но, кстати говоря,

вполне объяснимым, если рассматривать прямоугольную таблицу, см. рис.24). После изучения переместительного закона становится естественным, что оба выражения — 2 . 5 и 5 . 2 — являются решением задачи 2. Причем найти значение 5 . 2 через сумму легче, чем 2 . 5. В ответе же исходя из здравого смысла получают 10 к. Таким образом, наряду с записью 2 к. . 5 = 10 к. возможна запись 5 .2 к. = 10 к.

Особые случаи умножения и деления. Таблица умножения состоит, как известно, из отдельных таблиц умножения числа 2 на однозначные числа, умножения числа З и т. д. Случаи умножения единицы и десяти в таблицу не включаются, так как соответствующие результаты не высчитываются — они находятся по достаточно простым правилам. Умножение единицы и на единицу, десяти и на десять, нуля и на нуль, а также соответствующие случаи деления рассматриваются особо.

В вузовском курсе математики свойство а 1 = а формулируется в определении операции умножения. То, что 1 . а = а, доказывается исходя из этого определения. В этом же курсе правило умножения нуля и на нуль доказывается исходя из определения нуля и свойств операции умножения. деление нуля и невозможность деления на нуль обосновываются с помощью определения деления и умножения нуля на число.

В начальной школе такой подход к разъяснению особых случаев умножения и деления невозможен. Попытка обосновать, что а 1 = а и а 0= 0, опираясь на определение умножения через сумму, также невозможна: непонятно, что есть «сумма», у которой только одно слагаемое, или «сумма» без слагаемых. Поэтому эти случаи умножения, а также правило «на нуль делить нельзя» учащиеся должны просто запомнить.

Правила умножения единицы и нуля объясняются через сложение: 1. 4=1+1+1+1=4, 0. 5=0+0+0+0+0=0 и т. д.

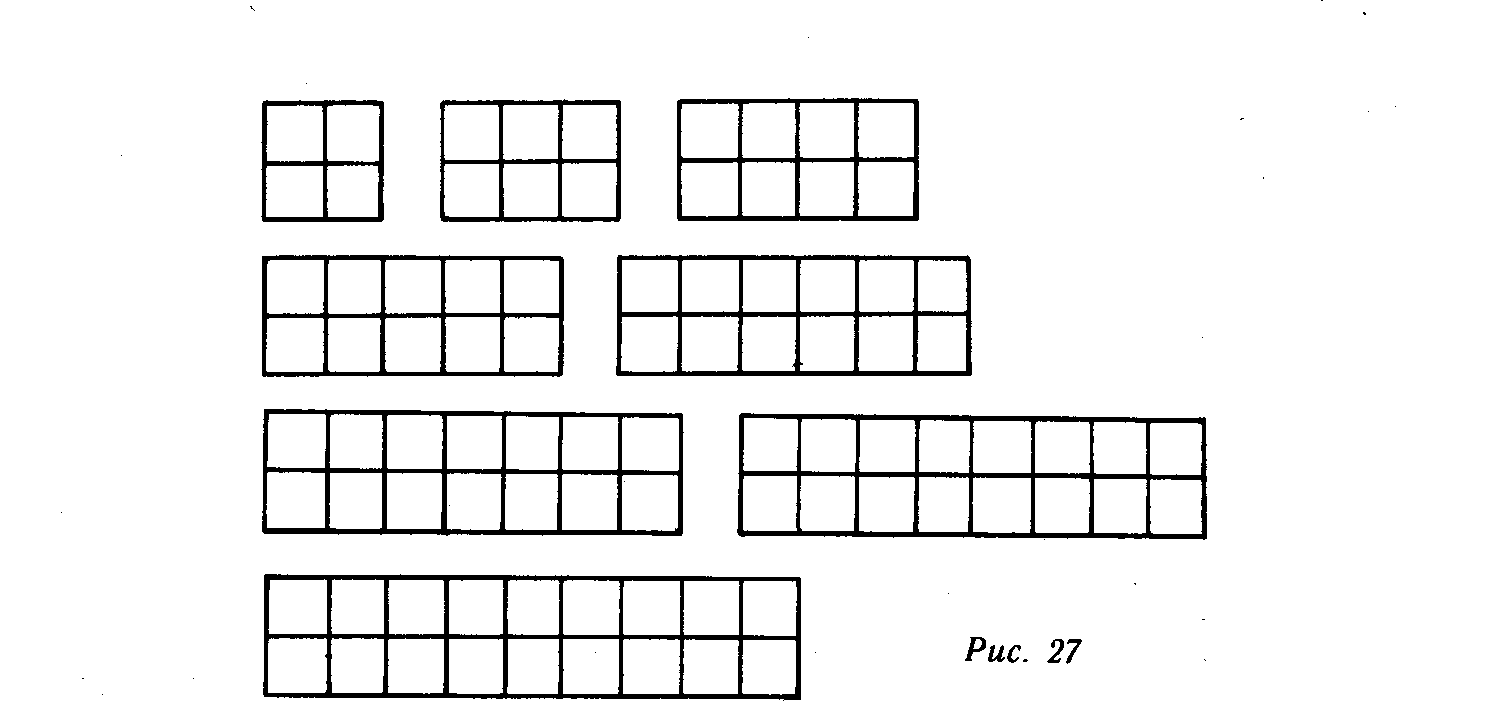
клетки (рис. 27). На первых порах с помощью этих прямоугольников подсчитываются значения произведений и частных. Они используются также для иллюстрации переместительного закона умножения, при изучении таблиц умножения трех, четырех и т. д.

Заучить таблицу умножения двух можно в результате многократного вычисления произведений и соответствующих частных. для этого необходимо использовать содержательные задачи. С одной стороны, они вносят разнообразие в работу, предупреждают зазубривание таблицы, с другой — учащиеся видят практическую значимость таблицы, необходимость ее запоминания.

Аналогично происходит знакомство с таблицами умножения трех, четырех, ..., девяти:

значения табличных произведений, соответствующих частных подсчитываются через сумму с помощью демонстрационной таблицы, прямоугольников;

анализируются связи между 5езультатами, уже полученными в данной таблице, различные способы их получения;

при работе над табличными случаями умножения и деления используются содержательные задачи;

для построения каждой новой таблицы используются результаты ранее изученных таблиц; за счет этого количество рассматриваемых случаев в каждой последующей таблице уменьшается.

Например, при построении таблицы умножения трех случай

3. 2 не рассматривается как новый этот результат был получен

в таблице умножения двух. При построении таблицы умножения

четырех не подсчитываются произведения 4. 2 и 4. 3. Таким образом, таблица умножения девяти содержит только один новый случай—9. 9

Уменьшение количества новых случаев от таблицы к таблице позволяет, с одной стороны, увеличить время на изучение новых таблиц и на закрепление уже изученных. С другой стороны, больше внимание уделяется решению задач, требующих знания таблицы умножения.

Внетабличное умножение и деление. Случаи умножения однозначного числа н однозначное являются табличными.

Таким образом, к внетабличным случаям относится умножение двузначного числа на однозначное. Прием устного умножения должен основываться на знании учащимися таблицы умножения. Поэтому двузначные множители необходимо привести к такому виду, который допускал бы использование таблицы умножения. для этого двузначные множители представляются в виде суммы разрядных слагаемых (одно из слагаемых однозначное число, второе

круглые десятки). При сложении и вычитании круглых десятков использовался прием замены круглых десятков однозначными именованными числами. Таким же образом умножение и деление круглых десятков на однозначное число может быть сведено к умножению однозначного именованного числа на однозначное: 40. 2 — 4 дес. 2 = 8 дес., т. е. 40 . 2 = 80. Умножение двузначного числа на однозначное выполняется так:

24 . 3= (20 + 4) .3 20 .3 +4 .3 60 + 12.

Операцию разложения числа на разрядные слагаемые учащиеся выполняют устно. К этому времени они умеют устно находить произведение однозначных чисел, сумму двузначных чисел. Поэтому для того чтобы сформировать у учащихся умение устно умножить двузначные числа на однозначные, необходимо ознакомить их еще с двумя операциями: умножением суммы на число и умножением круглых десятков на однозначное число. Методика изучения последней операции, как было показано выше, весьма проста, поэтому остановимся подробно на методике обучения умножению суммы на число.

Умножение суммы на число. Методика изучения этой темы (как и изучение всех математических понятий в начальной школе) основывается на использовании системы целесообразных задач, наглядных интерпретациях их содержания. Чтобы выяснить их особенности, воспользуемся определением умножения через сумму для случая, когда один из множителей представлен суммой:

(а+Ь)..с=(а+Ь)-.-(а+Ь)-4.-...--(а+Ь).

с раз

Правую часть этого равенства графически можно представить в виде с рядов объектов одного рода, причем в каждом ряду содержится а объектов одного вида и Ь объектов другого. В качестве таких объектов можно взять кружки двух видов светлые и темные (рис.28).

В соответствии с таким рисунком легко составить содержательные задачи, являющиеся средством формирования правила умножения суммы на число. Например: «В пионерском отряде 4 звена. В каждом звене 5 девочек и 4 мальчика. Сколько всего пионеров в отряде?», «На субботнике по благоустройству школьного двора каждому октябрятскому отряду было поручено посадить по 2 клена и по З липы. Сколько всего деревьев должны были посадить 5 отрядов?» и т. д. • Для каждой из таких задач составляются выражения двух видов (в соответствии с двумя возможными способами их решения), которые также можно проиллюстрировать графически: (5+4)•4 54+4•4 (2+3).5 2.5+3.5 и т. д. Соответствие двух разных выражений одной и той же конкретной ситуации делает факт равенства этих выражений очевидным. Затем учащимся предлагается самостоятельно составить содержательные задачи по выражениям вида (а + Ь). с и а• с + Ь . с. В заключение прием умножения суммы на число отрабатывается на числовых выражениях. Упражнения подбираются так, чтобы ученики могли выбрать наиболее удобный способ вычислений. Например, значение выражения (2 + 4). 6 удобнее вычислять как произведение (умножение б . б табличное) Значение выражения (9+5).8 определяется в три действия: 9•8+5.8, поскольку умножить 14 на 8 учащиеся еще не умеют. Правило умножения числа на сумму особо можно не рассматривать. Пользуясь переместительным законом умножения, младшие школьники самостоятельно могут преобразовать выражение (9+ + 5) 8 к виду 8 (9 + 5). Если же учитель найдет нужным подробно остановиться на содержании этого правила, то методика его изучения аналогична методике, рассмотренной выше. Алгоритм умножения двузначного числа на однозначное можно представить в виде последовательности операций: (1) - двузначный Ь— множитель представляется в виде суммы разрядных слагаемых; (2) сумма умножается по правилу умножения суммы на число;, (3) вычисляется произведение круглых десятков на число; (4) - определяется произведение однозначных чисел; (5) — вычисляется полученная сумма. Например:

На первых порах от учащихся можно требовать комментирования отдельных шагов алгоритма. деле н и е. При изучении деления в пределах 100 ученики должны овладеть приемами деления двузначных чисел на однозначные (в случаях, не являющихся табличными: 36:2, 45:3, 76:4 и Т. д.) И двузначных и двузначные. Частные, в которых делитель однозначное число, с методической точки зрения не оноронь1. Например, при делении 42 на 2 может быть использован прием, похожий на прием устного умножения: (40+2):2=40:2+2:2. Однако для случаев 84:3, 51:3, 30:2 такой прием нельзя применить. Таким образом, нужен такой прием устного деления, который был бы пригоден для всех случаев, когда делимое двузначное, а делитель — однозначное число. Очевидно, что в основе такого приема должно лежать разложение делимого на слагаемые, каждое из которых делится на делитель. В связи с этим учащихся необходимо предварительно ознакомить с правилом деления суммы на число: (а+ +Ь) :с. Деление суммы на число. Вначале изучения данной темы учащимся предлагается система целесообразных содержательных задач, например таких: «В одной вазе б слив, а в другой — 8. Эти сливы разделили поровну между двумя мальчиками. Сколько слив получил каждый мальчик?»; «Ученик купил тетради в линейку и клетку по цене З к. За тетради в линейку он уплатил 12 к., за тетради в клетку — б к. Сколько тетрадей всего купил ученик?»; «В два ларька привезли ящики с черешней по 4 кг в каждом. В один ларек привезли 12 кг черешни, а в другой — 24 кг. Сколько ящиков с черешней привезли в оба ларька?» и т. д. Под руководством учителя иллюстрируются два способа решения каждой задачи: (6+8) :2 и 6:2+8:2; (12+6):2 и 12:2+6:2; (12+24) :4 и 12:4+24:4. Так как каждое из двух выражений соответствует одной и той же реальной ситуации, то равенство их значений не вызывает сомнений. Обобщение двух способов решения разных по содержанию задач подводит к формулировке правила: чтобы разделить сумму на число, нужно на это число разделить первое и второе слагаемые и полученные результаты сложить. Рассматривается система упражнений вида (а + Ь): с ==? В одних случаях значение частного удобнее найти, не преобразуя частное, а в ‘других случаях — используя изученное правило. При этом школьники могут проговаривать правило, однако требовать его запоминания, очевидно, не стоит. деление двузначного числа на однозначное. Вначале предлагается самый простой вид внетабличных частных: е— 24:2, 33:3, 36:3, 48:4 и т. д. Школьники могут самостоятельно прийти к выводу, что деление в данных случаях можно выполнить с помощью приема, очень похожего на прием устного умножения: делимое представляется в виде суммы разрядных слагаемых, и деление выполняется по правилу деления суммы на число. Затем ученикам предлагаются частные, для которых этот прием неприменим: 78:3, 32:2, 92:2 и т. д. Одновременно учитель приводит доказательство того, что в каждом из этих случаев значение частного существует: 78:3= 26, так как 26. 3=78; 32:2= 16, так как 16. 2=32 и т. д. Используя опыт деления суммы на число, учащиеся могут предложить (к этому их нужно побудить, подтолкнуть) разложить делимое на удобных’ слагаемые, делящиеся на делитель. На конкретных примерах демонстрируется трудоемкость этого приема. Пусть, например, делимое 78 представлено в виде суммы 21 +57, тогда процесс деления будет таким: 78 : 3= (21 +57) : 3= 21 :3+ 57 : 3= внетабличное деление =7+(21+36):3=7+21:3+363= внетабличное деление =14-+(30+6):3=14+10+2=26. Прием разложения делимого на «удобные» слагаемые использовался в данном случае неоднократно. Возможно, что делимое было представлено не лучшим образом. Было бы легче, если бы оно было заменено суммой, в которой первое слагаемое являлось круглыми десятками, делящимися на делитель, например 60 или 30. Затем рассматривается частное, в котором делимое представлено суммой, одно из слагаемых которой круглые десятки, делящиеся на делитель. Причем замена делимого суммой выполняется различными способами: 96:3=(30+66):3==30:3+66:3=10+(30+36):3==10+30: :3 + 36:3 96:3= (60+36):3=60:ЗЧ-36:3=20-I-(30-i-6):3=20+30:3+ + 6:3 = 20+10+2 = 32 96:3=(90+6):3=90:3+6:3= 30+2=32. Очевидно, что самый простой случай — третий. Его особенность состоит в том, что одно из слагаемых не просто круглые десятки, делящиеся на делитель, а наибольшее количество десятков, делящихся на делитель. На конкретных примерах доказывается действенность разработанного приема (в числе примеров встречаются и частные вида 30:2, 50:2, 60:4, 60:5 и т. д.). При делении учащиеся могут проговаривать отдельные операции алгоритма: (1) делимое заменяется суммой, где одно из слагаемых наибольшее количество десятков, делящихся на делитель; (2) -- сумма делится по правилу деления суммы на число; (3) вычисляется частное круглых десятков на число; (4) вычисляется табличное частное; (5) вычисляется полученная сумма. Деление двузначного числа на двузначное. В начальных классах значение частного двузначных чисел определяется При этом используются знания учащихся о связи между умножением и делением: если частное подобрано верно, то при умножении его на делитель должно получиться делимое. Отметим, что вопрос о том, сколько цифр должно иметь частное, с учащимися не обсуждается. Приступая к изучению приема деления двузначного числа на двузначное, учитель предлагает учащимся достаточно простые частные, значения которых учащиеся в состоянии угадать, например 20:10, 60:30, 80:20,80:40и т. д. Затем учащимся предлагается доказать, что угаданное значение 108

частного верно. Здесь возможен, например, такой диалог учителя с учеником, Уч и т ел ь: Угадай, чему равно частное 20 и 10? У ч е н и к: Мне, кажется, частное равно 2. У ч и т е л ь: Как убедиться в правильности твоей догадки? У ч е н и к: Нужно выполнить проверку с помощью умножения. У ч и т ел ь: Как делается проверка? У ч е н и к: Частное умножается на делитель. Если получится делимое, частное угадано правильно; 2 умножить на 10— получим 20. Значит, 20: 10 равно двум. Аналогично выполняются и другие упражнения типа 22:11, 30:15, 24:12 и т. д. В случаях, когда угадать значение частного трудно, ученикам предлагается находить его подбором, перебирая однозначные числа по порядку, начиная, например, с двух. Когда у учащихся будет накоплен опыт, методика подбора может быть усовершенствована. Подбор например, можно начинать с числа 5, а затем, в зависимости от результата умножения 5 на делитель, следующее пробное число выбирать большим или меньшим 5. Например, при делении 98 на 14 предполагают, что частное равно.5:14•5=7О, значит, число 5 мало, нужно пробовать число 6:14.6=84—получено число меньше делимого, значит и б мало для значения частного. Пробуется число 7:14.7=98. Таким образом, 98:14=7. Можно подсказать учащимся, что при подборе значения частного следует обращать внимание на последние цифры делимого и делите- - ля. Так как делимое оканчивается цифрой 8, а делитель — цифрой 4, то достаточно вспомнить, какое число нужно умножить на 4, чтобы произведение оканчивалось цифрой 8. Таких чисел два — 2 и 7. Число 2 не подходит, так как слишком мало. Значит, частное равно 7. Выполняется проверка. Наиболее полно результаты изучения темы деления двузначного числа на двузначное могут быть использованы при обучении учащихся письменному делению. А оно изучается в концентре Многозначные числа. Поэтому, вероятно, деление на двузначные числа целесообразнее изучать непосредственно перед темой Деление многозначных чисел>. Деление с остатком. Эта тема используется при изучении алгоритма письменного деления. Изучая деление, необходимо рассмотреть с учащимися и случаи, когда одно число не делится на другое нацело. Тему Деление с остатком целесообразно изучать в два приема. В теме внетабличные случаи деления можно показать учащимся, что значит разделить с остатком, некоторые свойства такого деления. Компоненты при этом подбираются таким образом, чтобы для деления было достаточно знания табличных случаев (например, 25:4, 38:6, 71:8 и т. д.). Обратиться к теме деления с остатком в самом начале изучения операции деления важно еще и потому, что деление с остатком встречается в реальной жизни значительно чаще, чем удобное табличное деление. Вначале рассматриваются задачи такого содержания: У мальчика 20 к. Сколько тетрадей по цене З к. он сможет купить за эти деньги?»; «В коробке 25 конфет. Их разделили поровну между б детьми. Сколько конфет получил каждый из них?»; ‘В классе 35 учеников. Сколько парт должно быть в этом классе?» и т. д.

При решении задач используются наглядные средства. Например, первая из задач может быть проиллюстрирована с помощью кружков (однокопеечных монет) (рис. 29). I1ллюстраиия не только позво

ляет решить задачу, но и ввести понятие «остаток». Практическое решение задачи математизируется: 20:3 = б (ост. 2). В результате решения еще нескольких подобных задач учащиеся могут прийти к выводу, что для получения ответа совсем не обязательно представлять содержание задачи в наглядной форме.

Приведем фрагмент урока, на котором учитель подводит учащихся к «открытию» приема деления с остатком.

Таким образом, учащиеся приходят к выводу: чтобы число разделить на данное число (с остатком), нужно взять самое большое число, делящееся на делитель, но меньше делимого. Не обязательно заучивать это правило наизусть. Важно, чтобы ученики умели применять его на практике. В качестве тренировочных упражнений полезно рассмотреть такую систему частных, которая позволяет учащимся увидеть закономерность,, связывающую делитель и остаток:

У ч и т е л ь: Итак рассмотренная задача решается выражением 25:4 (рассматривалась, например, одна из задач, приведенных выше). Табличное ли это деление?

Ученик: Нет.

У ч и т е л ь: Сколько единиц нужно взять из 25, чтобы они целиком разделились на 4?

Уч е н и к: Например, 4, 8, 12, 16, 20, 24.

У ч и т е л ь: Если мы возьмем и разделим 4 единицы, то сколько единиц останется разделить?

Ученик: 21.

У ч и т е л ь: Сколько единиц можно взять из этого числа, чтобы они разде. лились на 4?

Ученик: Или 4, или 8, или 16, или 20.

У ч и т е л ь: А сколько единиц можно было бы взять из 25 для деления на 4, чтобы не делить на единицы по частям?

У ч е н и к: 24 единицы.

У ч и т е л ь: Чему равнялось бы частное?

У ч е н и к: б и одна единица осталась бы.

У ч и т е л ь: Если бы пришлось делить 37 на 4, то сколько единиц из этого числа нужно было бы сразу взять, чтобы получить самый маленький остаток?

У ч е н и к: Из всех чисел, которые делятся на 4, нужно было бы взять самое большое число, но чтобы оно было меньше 37. Это число 36.

Анализ результатов деления позволяет сделать вывод, что остаток при делении не может быть больше делителя (при условии, что максимальное число единиц делимого разделено на делитель).

Возможно, конечно, что кто-нибудь из учащихся получит «парадоксальный» ответ: 45:7= 5 (ост. 10). Чтобы помочь ему заметить ошибку, нужно обратить его внимание на то, все ли единицы делимостью разделены? 10 можно делить на 7, значит, частное подобрано неверно. Правильный ответ: частное 6, остаток 3.

16. ТЫСЯЧА

Общие положения. Известно, что наряду с концентрами «десяток» и «Сотня» в начальном курсе математики выделяется концентр «Тысяча». Это объясняется тем, что при изучении трехзначных чисел учащиеся усваивают качественно новые сведения из области нумерации чисел и очень важные алгоритмы выполнения арифметических операций.

Изучая нумерацию трехзначных чисел, ученики знакомятся с новым разрядом — сотен. Тем самым завершается формирование класса единиц. Это позволяет в дальнейшем делать более крупные шаги в изучении нумерации: числа, большие тысячи, будут вводиться не по разрядам, а по классам.

При изучении концентра «Тысяча» расширяются знания учащихся об операциях сложения и вычитания. Они усваивают приемы письменного сложения и вычитания, которые впоследствии используются и на множестве многозначных чисел.

Нумерация и сравнение чисел. При изучении нумерации чисел в пределах десяти естественными наглядными пособиями были множества реальных предметов, более абстрактные множества палочек, геометрических фигур. Изучение нумерации в пределах ста потребовало более сложных пособий, например, таких, как абак. Однако для того чтобы изобразить, например, число 500, потребовался бы абак с 50 карманами. Поэтому при изучении нумерации сложения и вычитания в пределах тысячи используется позиционный абак. Особенность его состоит в том, что наглядный материал, изображающий единицы, десятки и сотни, имеет один и тот же вид это или косточки счетов, или квадраты, или палочки. Зато карманы абака — их всего три — выполняют разные функции. Палочка, находящаяся в крайнем левом кармане (рис. 30), означает единицу. Если палочку положить в средний карман, она будет означать десяток, а если в крайний правый,—.- то сотню. Заметим, что принцип изображения чисел на непозиционном абаке был другим: карманам не приписывалось

для демонстраций у доски и индивидуальной работы удобен более простой вариант арифметического «ящика». Роль единиц играют квадраты, десятков полоски, состоящие из 10 квадратов. Большие Квадраты,* состоящие из 10 полосок или 100 маленьких квадратов, служат для изображения сотен. Эти материалы могут быть изготовлены из плотной бумаги или картона.

Нумерация чисел от 10 до 100 изучалась в три приема: нумерация 4 чисел второго десятка, круглых десятков, остальных двузначных чи4ел Это объяснялось тем, что образование названий чисел второго ,десятка, круглых десятков и остальных двузначных чисел имеет особенности. Названия трехзначных чисел образуются либо из названия круглы сотен, либо из названия круглых сотен и двузначных или однозначны чисел в сочетании. Поэтому знакомство учащихся с нумерации трехзначных чисел осуществляется в два приема. Сначала школьники учатся называть и записывать трехзначные числа, оканчивающиеся нулями, а потом остальные трехзначные чи сл а. Кр уг л ы е сот н и. Сущность методики знакомства учащихся ‘ числами этого вида состоит, во-первых, в том, чтобы показать им, что считать сотнями можно так же, как единицами и десятками, и что любое число сотен в пределах десяти имеет особое название. Вначале учащиеся подсчитывают количество квадратов, укладываемы по одному в наборное полотно: «Один, два девять». Затем в наборное полотно по одной укладываются полоски («десятки»). По мере заполнения полотна учащиеся считают: «Один десяток квадратов, два десятка квадратов девять десятков квадратов» Обращается внимание, что количество квадратов можно называют по-другому: «десять квадратов, двадцать девяносто квадратов». Рассматривается модель новой счетной единицы — больший квадрат (пластинка), состоящий из 10 полосок. Так как каждая полоска содержит 10 квадратов-единиц, то констатируется, что пластинка содержит 100 таких квадратов. Поэтому, когда в наборное полотно пластинки укладываются по одной, школьники считают: «0д- на сотня квадратов, две сотни квадратов девять сотен квадратов». Учитель говорит, что- число квадратов в каждом из этих случаев можно назвать: сто, двести девятьсот. Обращается внимание учащихся на особенности и сходство в названиях сотен: две-сти, три-ста, четыре-ста, пять-сот девять-сот. Одновременно с названием круглых сотен выполняются операции сложения и вычитания: 5 еот.+3 сот.=8 сот., 7 сот.—2 сот.= = 5 сот. и т. д. С помощью наглядных пособий учащиеся учатся отвечать на вопросы: «Сколько десятков в сотне, ..., какое число соответствует 20 десяткам, 50 десяткам, б сотням?» и т. д. Устная нумерация трехзначных чисел. Параллельно с заучиванием учащимися названий круглых сотен начинается работ над устной нумерацией остальных трехзначных чисел. Это связан с тем, что при счете сотнями у учащихся может сложиться впечатление, что за числом сто, например, непосредственно следует двести, за двести - триста и т. д. Появление названий трехзначных чисел происходит «естественно», при выполнении учениками упражнений такого вида: «Назови число квадратов, изображенных на наборном полотне» (рис. 34). Учащиеся отвечают: «сто и двадцать три», «триста и сорок», «двести и пять». Предлагается

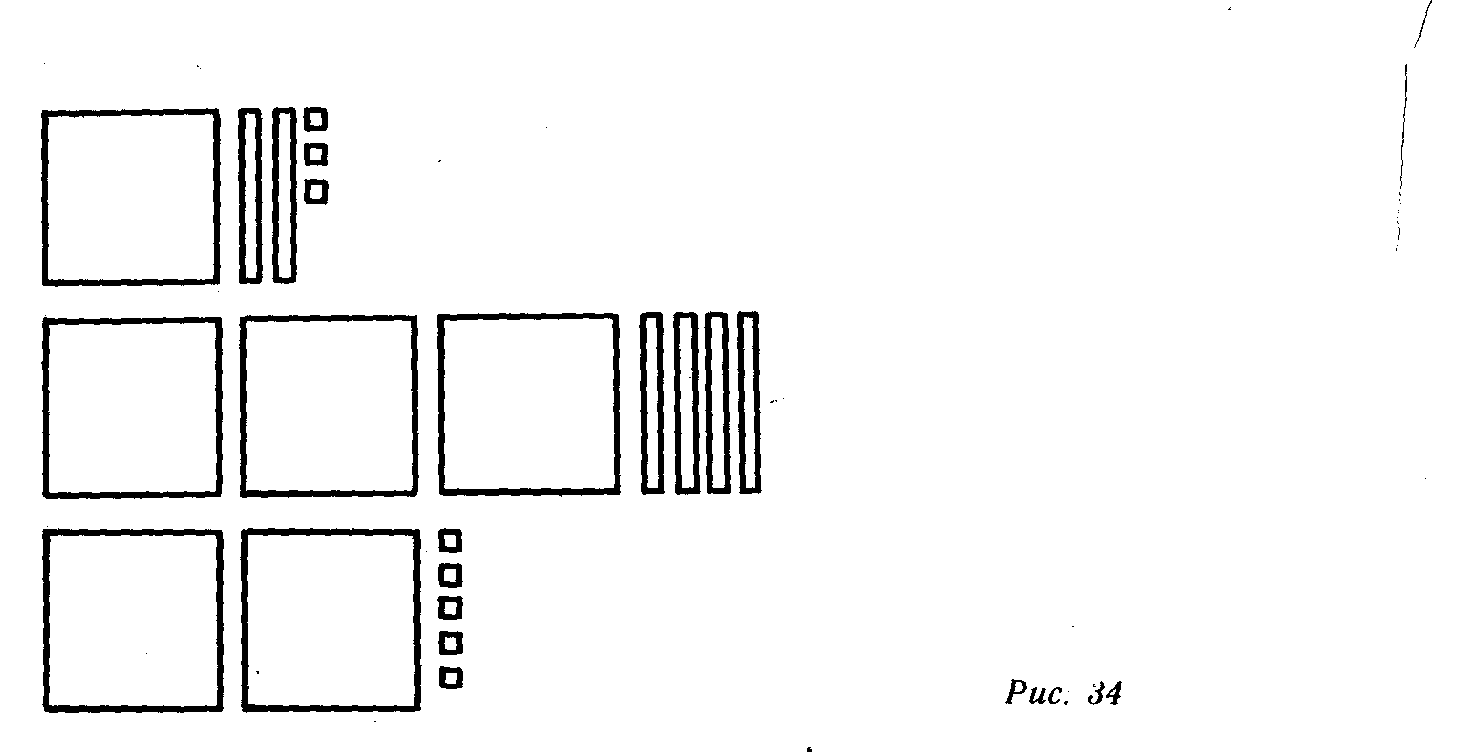
называть число квадратов без использования союза «и»: сто двадцать три, триста сорок и т. д.

Затем предлагаются более сложные упражнения: необходимо назвать число, состоящее из 2 сотен и 5 единиц; 7 сотен и 8 десятков; 9 сотен, 2 десятков и б единиц и т. д. По возможности эти упражнения выполняются без использования наглядных пособий.

Одновременно учащимся предлагаются упражнения другого рода. Они отвечают на вопросы: «Сколько сотен, единиц и десятков содержится в числах пятьсот сорок три, двести шестьдесят один, шестьсот два, сто семьдесят?»

Они также должны выполнять разнообразные упражнения.

Назови по порядку числа от девяносто семи до ста четырех, от ста девяносто девяти до двухсот трех и т. д.

Назови число, следующее за числом триста девяносто девять; число, меньшее на единицу, чем пятьсот; большее на два, чем восемьсот девяносто девять, и т. д.

Назови числа, которые находятся между числом триста двадцать шесть и триста тридцать один, и т. д.

для работы над этими упражнениями используются модели числового луча — числовая лента, рулетка.

Письменная нумерация трехзначных чисел. Работа над устной нумерацией проводится с опорой на арифметический ящик (его модификации). При изучении письменной нумерации используется позиционный абак. Прежде чем приступить к изучению записи трехзначных чисел, учащиеся учатся изображать на абаке число элементов некоторого множества, и наоборот, определять число элементов множеств по изображению на абаке. В качестве множеств могут использоваться множества квадратов, представленных отдельными квадратами, полосками и пластинками.

Обучение работе с абаком сводится к формированию у учащихся достаточно простого алгоритма. В абаке есть спицы. Крайняя справа предназначена для изображения количества единиц, т. е. отдельных квадратов. На нее нанизывается столько косточек, сколько отдельных квадратов изображено. На вторую спицу нанизываются косточки, которые показывают, сколько полосок (десятков), содержит данное число. Наконец на третью

спицу косточки, соответствующие

сотням (пластинкам) данного числа.

Все эти пояснения следуют по ходу изображения числа (квадратов) на абаке.

Например, на абаке нужно отложить число 567. для наглядности

его можно представить в виде множества квадратов (пластинок, полосок и отдельных квадратов). Затем, в соответствии с числом единиц (квадратов), десятков (полосок), сотен (пластинок), заполняются спицы абака (рис. 35).

В дальнейшем при выполнении подобных упражнений («Изобразите на абаке число») можно не представлять число в наглядном виде.

Полезны упражнения и другого вида: назвать число, изображенное на абаке. Операции рассмотренного алгоритма выполняются в обратном порядке: сначала подсчитывается количество косточек на спице сотен и называется число сотен в числе, затем - количество косточек на спице десятков и называется число десятков и т. п. Рядом с соответствующими спицами абака записываются цифры.

Учащимся предлагается записывать в тетради цифры, соответствующие показаниям абака, в таком же порядке (слева направо),

в каком расположены на абаке спицы сотен, десятков и единиц.

Каждую цифру пишут ‘в отдельную клетку тетради. Так появляются

записи: 667, 445 и т. д. Трехзначные числа на первых порах читаются

с опорой на абак.

Поясним последнее на примере. На доске записывается число 327. Требуется объяснить, что означает эта запись.

У ч и тел ь: Что означает цифра 3?

У ч е н и к: Это означает, что на спице сотен три косточки.

У ч и т е л ь: Что показывают эти косточки?

Учен и к: В числе З сотни.

У ч и тел ь: Что означает цифра 2?

Уч и тел ь: Какое же число записано на доске?

Уче н и к: Триста двадцать семь.

С помощью абака рассматривается запись трехзначных чисел особого вида: 200, 209, 290, 400, 470, 407, 500, 505 и т. п. При необходимости снова можно использовать арифметический «ящик».

Например, ставится задача изобразить на абаке и записать число двести. В этом числе 2 сотни, значит, на спице сотен абака откладываются две косточки. Нужно ли откладывать косточки на спице десятков? Очевидно, что нет, так как свободных десятков в числе двести нет. Все они заключены в двух сотнях — двадцать полосок объединены в две пластинки. Такое объяснение позволяет избежать неверной формулировки: <в числе двести нет десятков. Аналогично объясняется отсутствие единиц в разряде единиц числа

200. В соответствии с иллюстрацией на абаке записывается число 200.

В дальнейшем, когда учащиеся смогут записывать и читать трехзначные числа без опоры на абак, они учатся представлять такие числа в виде суммы разрядных слагаемых.

Из концентра «Сотня известно, как на языке математики записывается, что число 46, например, состоит из 4 десятков и б единиц:

46=40+6. Этот способ обобщается для трехзначных чисел: число

256 состоит из 2 сотен, 5 десятков и б единиц, поэтому 256= =200+50+6. Рассматриваются и более сложные случаи: 206= 200+6, 250=200+50 и т. д. Одновременно изучаются и случаи вычитания, основанные на знании разрядного состава трехзначного числа:842—2=840,842—4О=8О2,842—8ОО=42,57О__7О5у 570—500=70, 409 —9=400, 409—400=9 и т. д.

При выполнении упражнений такого рода учащиеся, с одной стороны, закрепляют знание разрядного состава и поместного значения цифр в трехзначном числе, с другой,— готовятся к изучению операций сложения и вычитания на множестве трехзначных чисел.

Важную роль в изучении нумерации трехзначных чисел играют составные именованные числа, выраженные в мерах длины, стоимости. Использование таких чисел возможно на любом этапе знакомства учащихся с позиционным принципом нумерации. В частности, использование мер длины может помочь учащимся представлять некоторые трехзначные числа в виде двузначных именованных чисел. Такой прием в дальнейшем используется для вычисления значения сумм и разностей определенного вида. Например, чтобы показать, что число 490 содержит 49 десятков и может быть представлено в виде 49 десятков, рассматривается следующая система упражнений: «Сколько дециметров содержится в 4 м и 9 дм? в 490 см? в 590 см?> и т. д.

Сравнение чисел в пределах 1 000 осуществляется аналогично сравнению чисел в пределах 100. Прежде всего необходимо установить, что всякое трехзначное число, даже самое маленькое, больше любого, даже самого большого, двузначного числа (100 99). Этим самым сравнение чисел в пределах 1000 сводится к сравнению трехзначных чисел.

На примерах выясняется, что из двух трехзначных чисел то

больше, у которого цифра сотен больше (321 285, 505 з 396 и т. п.). Если же цифры сотен двух сравниваемых чисел равны, то сравниваются цифры десятков, и то число больше, у которого цифра десятков больше (485 478, 315з 308 и т. п.). Если же и цифры десятков равны, то сравниваются цифры единиц, и то число больше, у которого цифра единиц больше (576 572, 105 101 и т. п.).

два трехзначных числа равны тогда и только тогда, когда цифры и одноименных разрядов (сотен, десятков, единиц) равны (одинаковы).

Описанный алгоритм можно представить (для учителя, конечно) в виде схемы (рис. 36). Пусть необходимо сравнить два трехзначных числа: А1 = х1с11е и А2 = с2сi2е2, где с!, й, е1 —

цифры сотен, десятков и единиц числа А1, а с2, i2, е2.— цифры сотен, десятков и единиц числа А2.

Однако эта схема алгоритма построена нерационально, хотя по дидактическим соображениям более понятна. Циклический характер процесса сравнения отражается в более простой схеме (рис. 37). Введем следующие обозначения: А и В — сравниваемые числа А = а2аiао, В = Ь1Ь2Ь0. Этот алгоритм легко обобщается для сравнения двух многозначных чисел: А В = ... Ь1Ь0 (рис. 38).

Сложение и вычитание (устные вычисления). В концентре «Тысяча» учащиеся овладевают принципиально новыми умениями— письменного сложения и вычитания чисел. Вместе с тем раскрываются широкие возможности для упражнения школьников в устном счете в новых условиях — на множестве трехзначных чисел. Учитель должен Использовать эти возможности. Это, во-первых, позволяет закрепить навыки устного счета, которые учащиеся приобрели в концентре «Сотня». Во-вторых, такой счет полезен при усвоении нумерации Трехзна4ных чисел, принципа позиционного счисления. В-третьих, у учеников вырабатывается привычка обращаться к письменным вычислениям лишь тогда, когда ВЫПОЛНИТЬ вычисления устно трудно.

Выделяют две группы сумм и разностей, значения которых учащиеся должны уметь вычислять устно.

К первой группе относятся суммы и разности, значения которых определяются в буквальном смысле слова без вычислений. Для этого используется знание разрядного состава чисел, позиционного принципа записи чисел. Эти суммы и разности имеют вид: 400+2, 400+ 20, 400+ 25, 405+ 20, 450+ 2, 420—.-20, 420—400, 402—2, 402 — 400, 425 — 5, 425 — 20, 425 — 400. Значения подобных выражений вычисляются еще в период учащимися нумерации трехзначных чисел. Затруднения в такого рода вычислениях свидетельствуют о том, что ученик плохо усвоил нумерацию. В этих случаях необходимо обратиться к помощи абака.

Вторая группа включает следующие выражения: 70+50,1 120—70, 560+240, 560—240, 670+ 190, 670—190 и т. д. Их значения определяются на основе знания учащимися табличных случаев сложения и вычитания или приемов устного сложей1ВБТЯiВТЯ в пределах ста. Однако эти знания нельзя применить к данным выражениям непосредственно. Выражения приводятся к удобному виду с помощью уже известного приема замены двузначного числа однозначным именованным числом. Рассмотрим использование этого

приема на конкретных примерах:

500 — 300

5 сот.—З сот.=2 сот.

500—300= 200

таблица сложения и вычитания;

240 + 380

24 дес.+38 дес.=62 дес.

240+380= 620

620 — 380

62 дес.—38 дес.=24 дес.

620—380= 240

Здесь используются приемы устного сложения и вычитания.

Суммы и разности такого вида мо>но рассматривать сразу после усвоения нумерации трехзначных чисел.

Умножение и деление (устные вычисления). Прием сведения новых случаев сложения и вычитания к ранее изученным может быть использован и для некоторых случаев умножения и деления в пределах тысячи. Так, произведения и частные вида 200. 3, 600:3, 70.5, 350:7 можно представить как 2 сот.:3, б сот.:3, 7 дес. 5, 35 лес. :7. Для их вычисления достаточно знать таблицу умножения и соответствующие случаи деления.

Произведения и частные вида 120.3, 240.2, 170.5 и 360:3, 720:8, 560:7 с помощью того же приема представляют как произведения и частные двузначных и однозначных чисел. Для их вычисления используются приемы устного умножения и деления.

Письменные приемы (сложения и вычитания). Алгоритмы сложения и вычитания в столбик, усвоенные учащимися в начальных классах, используются на протяжении всех лет обучения математике в средней школе. Качество усвоения этих алгоритмов в значительной степени зависит от того, насколько ясно они представлены ученикам. Важную роль при этом играют средства наглядности и главным образом позиционный абак.

500 + 300

5 сот.+3 сот.=8 сот.

500+300= 800

Здесь используется

80 + 90

8 дес.+9 дес.=17 дес.

80+90= 170

170—90

17 дес.—9 дес.=8 дес.

170—90= 80

Определим последовательность и методику изучения различных

ВИДОВ сумм в порядке Возрастающей СЛОЖНОСТИ.

‘_- Сначала рассматриваются самые простые случаи: 256+300,

256+40, 256+1. Нахождение ЭТИХ сумм Легко Иллюстрируется с

Помощью абака. К уже имеющимся на абаке КОСТОЧКАМ показывающим Первое слагаемое 256, Последовательно присоединяют

З КОСТОЧКИ на СПИЦУ СОТЕН, ИЛИ 4 КОСТОЧКИ на спицу Десятков, или одну на спицу единиц. Затем ЭТИ случаи обобщаются - к числу

256 прибавляется 341. Манипуляции с абаком (рис. 39) описываются

математически

256+З41 (200+ЗОО)+ (50+40) + (б+I)==5ОО+9О+7=597

Очевидно, Правило прибавления суммы к сумме МОЖНО было бы ввести через задачи. С помощью Системы Целесообразных задач

задач

можно было бы также Показать, ЧТО этим правилом в некоторых случаях удобно Пользоваться для Вычислений И, наконец, МОЖНО было бы Побудить учащихся ЗАПОМНИТЬ формулировку этого Правила. Однако все ЭТО Оказывается ИЗЛИШНИМ, если Использовать абак. С его помощью прием Письменного сложения МОЖНО представить очень наглядно

действия, выполненные на

абаке, Записываются и по-другому — столбиком (см. РИС. 39). Аналогичная Запись появляется на тетрадях учащихся. Запись в тетрадях учитель сопровождает объяснением, как следуетподпц1..

объяснением, как следуетподпц1.. одно слагаемое Под другим: числа б и 1 записываются СТРОГО одно под Другим, Потому что б Косточек и одна нанизаны на одну и ту же спицу абака. Поясняется, почему цифра 4 подписывается ПОД цифрой 5, а З - ПОД цифрой 2, зачем ПРОВОДИТСЯ горизонтальная Черта - она Отделяет Слагаемые от значения Суммы, Где Ставится знак действия. Сложение в столбик гораздо удобнее и нагляднее, чем сложение в строчку.

Навыки записи Слагаемых и значения Суммы в столбик закрепляются при вычислении сумм аналогичного вида (сумма единиц одноименного разряда слагаемых меньше 10).

Следующим ПО СЛОЖНОСТИ ВИДОМ сумм является сумма, в Которой При сложении единиц какого-либо разряда - Образуется единица старшего Разряда: 354+236, 354+237, 354+452, 354+462.

Учащимся следует напомнить, ЧТО при сложении однозначных Чисел, Например 5 и 8, получается Двузначное число, т. е. образуется единица старшего разряда - разряда Десятков, Эта единица записывается на соответствующем месте. Ученики знают также, как найти сумму, например, чисел 25 и 8. При сложении 5 и 8 также получается новый десяток, который приплюсовывается к уже имеющимся двум десяткам. Все ЭТО позволяет упростить объяснение приема вычисления сумм нового вида. И все же на первых порах не стоит запрещать учащимся записывать промежуточные результаты сложения. Необходимо также побуждать учащихся использовать индивидуальные абаки. На демонстрационном абаке (рис. 40, а) изображается, например, сложение чисел 354 и 236. По ходу

работы с абаком учитель дает следующие пояснения: «На спице единиц оказалось 10 косточек, т. е. десяток. Но десяток изображается на абаке одной косточкой на спице десятков. Значит, к тем косточкам, которые, находятся на спице десятков—их 8, нанизываем еще одну косточку, а со спицы единиц все косточки снимаем.

Для нескольких примеров такого рода учащиеся могут делать подробную запись, фиксируя промежуточную сумму (рис. 40,а). Выполняемые операции комментируются ими, например, следующим образом: «К б прибавить 4, получится 10. В разряде единиц записываю ноль, а один десяток запоминаю. К 5 прибавить 3, получится 8, и еще один десяток — получится 9. В разряде десятков записываю

9. К З сотням прибавить 2, Получится 5 сотен. В разряде сотен записываю 5. Ответ 590.

В дальнейшем они проговаривают промежуточные операции более кратко: «К 4 прибавить 6—10, 0 пишу, 1 запоминаю. К 5 прибавить 3—8, и еще один — 9. К З прибавить 2—5. Сумма равна 590».

Вычисление сумм вида 354 + 237 несущественно отличается от рассмотренных выше.

При вычислении сумм, в которых при сложении десятков образуется сотня, полезно обратиться к абаку. Так же как и в предыдущем случае, несколько примеров можно выполнить с записью промежуточной суммы (рис. 40, 6).

Наконец, рассматривается самый сложный случай сложения трехзначных чисел, когда при сложении разрядных единиц образуется и десяток и сотня: 354 +246, 354 +267 и т. д.

Сначала сложение выполняется на абаке (рис. 41, а). Последовательно объясняется замена 10 единиц десятком (рис. 41, 6), а

затем 10 десятков—сотней (рис. 41, в). В записи действия в столбик каждая из ситуаций, представленных на абаке (рис. 41), фиксируется в виде промежуточной суммы. Эти записи подробно комментируются.

После детального рассмотрения еще одного-двух примеров промежуточные суммы не записываются, а запоминаются. При необходимости учащиеся дают краткие пояснения. Например, для случая

354+267: «к 4 прибавить 7—! 1. Один пишу, один запоминаю. к 5 прибавить 6—1 1 и еще один 12, два пишу, один запоминаю. К З прибавить 2—5 и еще 1—6. Сумма равна 621».

В процессе закрепления приема сложения в столбик будут встречаться и другие «особые» случаи, например 295+405, 585+ 15,308+407 и т. д. Не исключено, что в некоторых из этих случаев ученикам снова придется обратиться к абаку.

В заключение учитель на конкретном примере объясняет, почему сложение в столбик начинается с единиц младшего разряда.

Если начать складывать числа 367 и 594 с разряда сотен, то в сумму придется дважды вносить поправки: 367

+ 594

961

Если же начать сложение с единиц, этого можно избежать.

При изучении приема письменного вычитания, так же как и при сложении, последовательно рассматриваются разные по сложности случаи.

Самый простой случай, например 382—261, 427—225, учащиеся в основном могут объяснить самостоятельно. действия иллюстрируются с помощью абака и записываются на математическом

языке (рис. 42):

382—261 =(300—200)+

+ (80—60) + (2— 1) = 100 +

+20+1 = 121.

(Знакомить учащихся с какими-

либо новыми «правилами» сложения

и вычитания нет необходимости. Операции, выполняемые на абаке, естественны, и смысл их очевиден.)

По аналогии со сложением в столбик видно, что записывать операцию вычитания экономнее столбиком. Учащиеся, вероятно, способны объяснить, как записывается вычитаемое под уменьшаемым. Вычитание, подобно сложению, начинается с разряда единиц.

Рассматриваются более сложные случаи вычитания, когда в одном из разрядов уменьшаемого меньше единиц, чем в соответствующем разряде вычитаемого: 382—263, 382—291 и т. д. Объяснить особенность вычислений в этих случаях можно проще, если связать их с уже изученным приемом сложения в столбик с образованием дополнительных разрядных единиц.

Приведем фрагмент такого объяснения.

Уч ител ь: Сложи 356 и 227 на абаке. Прокомментируй выполняемые действия.

Ученик: К б прибавить 7—получим 13. 13 косточек составляют десяток и три единицы. На спице единиц оставляем З косточки, а снятые 10 косточек заменяем 1 косточкой, которую нанизываем на спицу десятка, и т. д.

Затем на абаке выполняется обратное действие: из 583 вычитается, например, 277. Из З вычесть 7 нельзя. Выход — в использовании правила замены 10 единиц десятком в обратном порядке. Теперь десяток заменяется 10 единицами. На спице единиц становится 13 косточек, зато на спице десятков — на 1 косточку меньше (рис. 43). Вначале промежуточное преобразование уменьшаемого можно записать. В дальнейшем оно выполняется в уме. Чтобы не забыть, что в старшем разряде была занята единица, над этим разрядом ставят точку

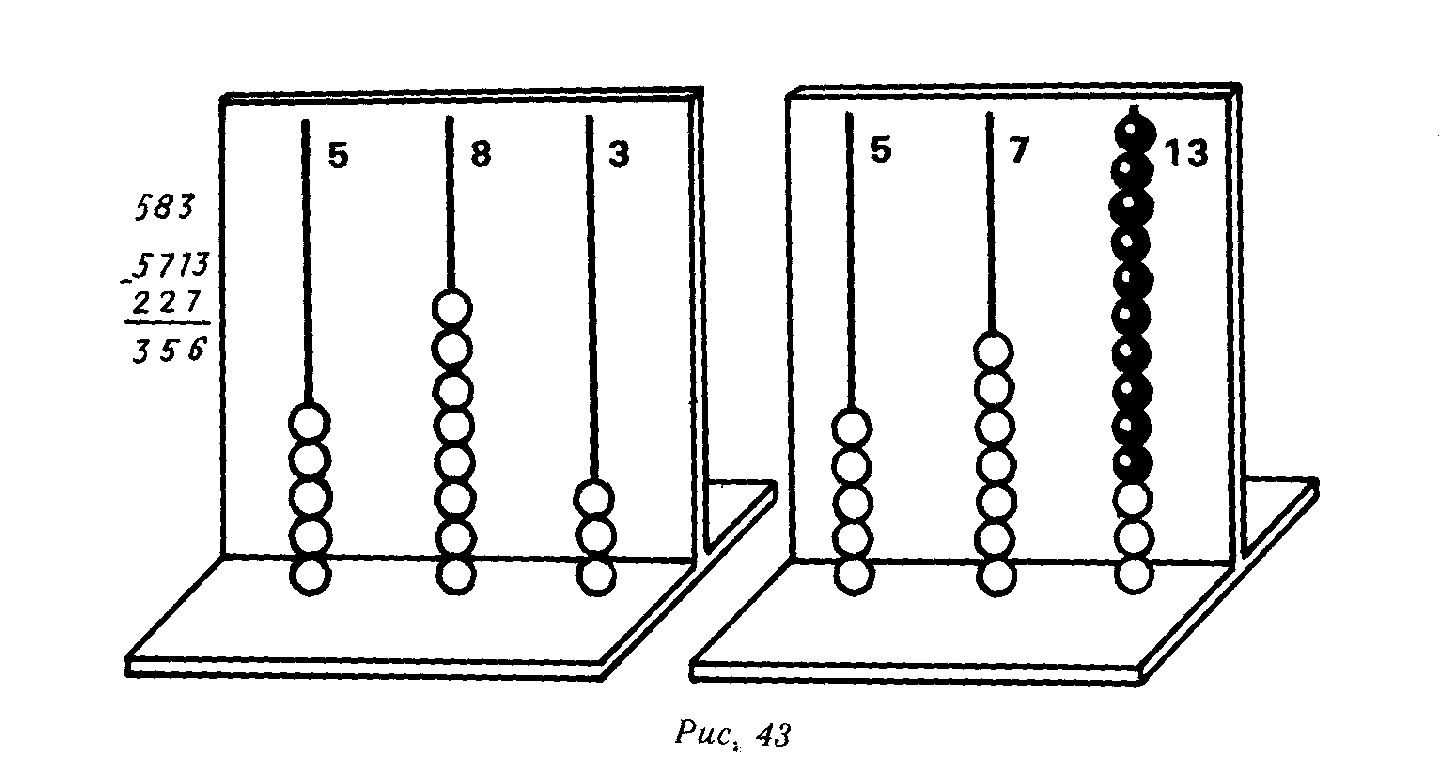
Затем изучается случай, когда в уменьшаемом занимается единица из разряда сотен. Решая первые примеры, учащиеся подробно комментируют выполняемые операции: «836—354. От б отнять 4, получится 2, 2 записываю в разряд единиц. От З отнять 5 нельзя. Занимаю от 8 одну сотню. Ставлю над 8 точку это значит, что осталось 7 сотен. Сотню дроблю на 10 десятков. От 13 десятков отнять 5, получится 8. Записываю 8 в разряд десятков. От 7 сотен отнять 3, получится 4 сотни. Записываю 4 в разряд сотен. Ответ:

В дальнейшем ученики лишь изредка, в случае затруднений, комментируют применение алгоритма, да и то в краткой форме:

От б отнять 4, получу 2. От З отнять 5 нельзя, занимаю сотню. От 13 отнять 5—8. От 7 отнять 3—4>.

Подробно рассматривается случай, когда в двух разрядах уменьшаемого меньше единиц, чем в соответствующих разрядах вычитаемого: 564—267, 682—393, 407—149 и т. д.

Операции алгоритма иллюстрируются на демонстрационном абаке, на доске выполняются соответствующие математические записи (рис. 44). Используя опыт, приобретенный при изучении предыдущих случаев вычитания в столбик, учащиеся могут самостоятельно пояснить сущность и последовательность операций алгоритма. Содержание этих пояснений может, например, быть таким:

От 4 отнять 7 нельзя. Займем один десяток и раздробим его на 10 единиц. Всего стало 14 единиц. От 14 отнять 7, получится 7. Вычитаем десятки. От 5 отнять б нельзя. Займем одну сотню и раздробим ее на 10 десятков. Всего стало 15 десятков. От 15 отнять б, получим 9. От 4 сотен отнять 2 сотни, получим 2 сотни. Ответ: 297>.

Затем прием отрабатывается без выполнения промежуточных

записей. Если возникают затруднения, от учащихся можно потребовать прокомментировать выполняемые вычисления с помощью абака.

Учителю необходимо подробно остановиться еще на одном случае вычитания, когда недостающие в уменьшаемом единицы нельзя

занять из соседнего разряда: 307—189, 600—231 и т. д. Под

руководством учителя учащиеся ВЫПОЛНЯЮТ операции на демонстрационном абаке (и индивидуальных абаках), математически записывают промежуточные действия и дают соответствующие пояснения (рис. 45). После выяснения особенностей этого приема следует особо оговорить оформление записи в столбик, когда промежуточные действия выполняются в уме. учащимся может быть предложен, например, такой вариант записи:

.9

600

238

362

По мере усвоения школьниками новых случаев упражнения на письменное сложение и вычитание разнообразятся. Так, ученикам предлагается выполнять проверку вычисленного результата с по- мощью обратного действия. Вычисляются значения выражений, содержащих несколько действий сложения и вычитания.

Операции над именованными числами выполняются после перевода обоих компонентов в более мелкие единицы. Однако нужно практиковать сложение и вычитание в столбик и без перевода. Это позволит учащимся наглядно представить понятие «разрядные единицы». Так, в данном случае единицы разряда единиц — это сантиметры, единицы разряда десятков дециметры, единицы разряда сотен метры:

м 7 дм 8 см

б м 9 дм 4 см

10 м 7 дм 2см

(Учащиеся незаметно для себя получили число больше тысячи. Это, конечно, полезно, если иметь в виду изучение в дальнейшем операций над многозначными числами.)

Одновременно с совершенствованием навыков письменного сложения и вычитания ученики должны закреплять вычислительные навыки, приобретенные при изучении предыдущих концентров. Это относится к приемам устного сложения и вычитания. Выше было показано, как организовать такую работу при изучении трехзначных чисел. Учащихся полезно побуждать к использованию правил прибавления числа к сумме и суммы к числу, вычитания числа из суммы и суммы из числа, облегчающих вычисления. Например:

(385+ 37) +63,885— (135+ 257), 126+253+344+ 207 и т. д. Такие упражнения могут выполняться устно.

7. МНОГОЗНАЧНЫЕ ЧИСЛА

Общие положения. Изучая материал концентров «десяток», “Сотня», «Тысяча», учащиеся ознакомились с цифрами десятичной системы счисления, разрядами единиц, десятков, сотен. Сейчас же им предстоит усвоить понятие классов чисел. Это понятие позволяет перейти к нумерации сколь угодно больших натуральных чисел. Поэтому в ко те«Мнщiыыаiкла» заканчивается изучение н ме а ни целых не т и ате предыдущих концентрах учащиеся запоминали таблицу сложения (вычитания), умножения (деления), овладевает устного выполнения эти операций, приемами письменного сложения и вычитания. В концентре Многозначные числа» эти знания и умения обобщаются для компонентов,, имеющих более трех цифр. Здесь же ученики овладевают алгоритмами письменного умножения и деления самыми сложными в конце математики начальной

Нумерация и сравнение. При изучении нумерации многозначных чисел удобно использовать нумерационную таблицу, которая заполняется карточками с цифрами (табл. 4). Отметим, что в соответствии с программой 1986 г. нумерация изучается в пределах миллиона.

Возможно, что некоторые учащиеся встретятся с трудностями

Изучение нумерации многозначных чисел следует предварить

краткой, но яркой беседой о значении больших чисел. Материал для

такой беседы учитель может почерпнуть из справочников по промышленному и сельскохозяйственному развитию нашей страны, стран СЭВ, газетных и журнальных статей и т. д. Нужно показать учащимся, что без использования таких больших чисел, как миллион, сотни тысяч, невозможно выразить количество той или иной прОдуКi-1ии, выпускаемой нашими заводами, производимой в колхозах и совхоза х.

Переходя к изучению нумерации, необходимо вспомнить некоторые свойства позиционной системы счисления:

1) значение цифры в числе определяется ее местом в этом числе;

2) названия чисел, обозначаемых Одной, двумя и тремя цифрами, образуются по определенным правил ам;

3) прибавление к 9 единицам еще одной единицы данного разряда дает единицу следующего, более старшего разряда.

Для этого учащимся предлагаются например, такие упражнения (для устного счета).

1. Что означает цифра 3(5, 7) в числах 537; 735; 375? Сколько единиц каждого разряда в числах 573; 872, 670 и т. д.?

Сколько сотен, десятков, единиц в числах 674; 609; 70 и т. д.?

Какое число содержит б сотен; 8 десятков; 54 десятка; 2 сотни, б десятков и 4 единицы; 2 сотни и 8 единиц и т. д.?

В виде суммы каких разрядных слагаемых можно представить числа 823; 321; 149, 303 и т. д.?

2.длина отрезка 15 мм. Как по-другому можно выразить его длину? Как можно выразить длину отрезка в 206 см; 29 дм; 400 см; 400 дм и т. д.?

Как называется число, в котором 10 десятков; 10 сотен; 60 десятков и т. д.?

3. К 9 единицам прибавили единицу; к 8 десяткам прибавили 2 десятка; к 4 сотням прибавили б сотен и Т 1 Как наТяют При изучении нумерации многозначных чисел можно выделить два Сначала учащиеся учатся называть и записывать многотичные числа, не имеющие единиц в разрядах класса единиц, т. е. числа, оканчивающиеся тремя нулями. Вспомним, как начиналось знакомство учащихся с нумерацией чисел в пределах 100, 1000. Рассматривались соответственно понятия «десяток», «сотня», Десяток и сотня использовались затем как счетные единицы.

Первые числа класса тысяч образуются в результате счета тысячами: одна тысяча, две тысячи десять тысяч. Одновременно заполняется косточками спица тысяч абака. При получении 10 тысяч, согласно правилу работы с абаком, десять косточек на спице

тысяч заменяются одной косточкой на спице более старшего разряда — десятков тысяч.

Далее счет продолжается уже десятками тысяч: десять тысяч, двадцать тысяч сто тысяч. На соответствующую спицу абака последовательно нанизываются косточки. Когда их оказывается десять, они заменяются одной косточкой, которая нанизывается на спицу более старшего разряда —- сотен тысяч.

Затем учащиеся считают сотнями тысяч. Одновременно заполняется соответствующая спица абака. Как только на ней появляется 10 косточек, все они заменяются одной косточкой на следующей спице. Число, которое эта косточка обозначает, называется миллионом.

Таким образом, ученики знакомятся с названиями новых разрядов единиц тысяч, десятков и сотен тысяч и учатся заполнять соответствующие спицы абака.

Далее учащиеся учатся называть числа вида 11 тысяч, 24 тысячи, 347 тысяч и т. д. Для этого используются следующие упражнения. На спицы единиц, десятков и. сотен тысяч абака нанизаны соответственно 5, 3 и 7 косточек. Спрашивается, какое число изображено на абаке. Учащиеся рассуждают: в этом числе 7 сотен тысяч, З десятка тысяч и 5 тысяч. Учитель объявляет, что такое число называется семьсот тридцать пять тысяч.

Одновременно учащиеся работают над упражнениями другого рода: называется число, обозначающее некоторое количество тысяч, нужно отложить соответствующее количество косточек на спицах абака.

В процессе такой работы школьники должны увидеть сходство в образовании названий чисел первого и второго класса: для единиц тысяч не существует специальных названий, они называются так же, как единицы первого класса, но с прибавлением слова «тысяча»; нет специальных названий и для десятков тысяч: для них используются названия десятков первого класса с прибавлением слова «тысяча» и т. д.

Для закрепления этих знаний может быть составлена, например, следующая таблица:

Вместе с тем важно показать различие между одноименными разрядами классов единиц и тысяч. Для этого на абаке откладываются, например, числа: 120 тысяч и 120, 50 тысяч и 50, 178 тысяч и 178. Обсуждается сходство и различие в изображении этих чисел. Сходство состоит в том, что на спицах соответствующих разрядов класса единиц и тысяч отложены одинаковые количества косточек. Однако 8 косточек для числа 178 означает количество единиц в разряде единиц, а для числа 178 тысяч количество тысяч в разряде единиц тысяч. Далее учащиеся записывают многозначные числа, оканчивающиеся тремя нулями. В изображении числа 5 тысяч на абаке в младших разрядах отсутствуют косточки. Это означает, что в этих разрядах О единиц. Обозначение этого числа цифрами выполняется в нумерационной таблице. В связи с.использованием этой таблицы вводится понятие класс», еще раз обсуждается сходство и различие в значении разрядов разных классов. После заполнения абака и таблицы учащиеся записывают данное число в тетрадях. Для удобства записи многозначного числа между группами цифр разных классов оставляется промежуток (например, клетка тетради). Аналогично приходят к записи чисел вида 700 тысяч, 107 тысяч, 420 тысяч, 567 тысяч и т. д. Основным средством наглядности при этом является нумерационная таблица. г Одновременно с изучением нумерации можно рассмотреть приемы устного сложения и вычитания многозначных чисел. Эти приемы основаны на знании учащимися разрядного состава многозначных чисел и применимы лишь в случаях следующего вида: 200000+ + 300 000, 100 000 + 50 000+7 000, 600 000—400 000, 350 000— —50 000, 342 000—42 000 и т. д. Вычисления при необходимости легко иллюстрируются с помощью абака и нумерационной таблицы. Устное вычисление значений таких выражений способствует усвоению нумерации и подготавливает учащихся к выполнению письменного сложения и вычитания многозначных чисел. Умножение и деление вида 5000. 2, 80 000:4, 17000. 3, 150 000:5 не требует специального приема и целиком опирается на знание учащимися названий соответствующих многозначных чисел и таблицы умножения и деления, приемов устного умножения и деления. Вместе с тем эпизодическое решение таких примеров облегчает усвоение нумерации, изучение последующих тем, связанных с умножением многозначных чисел. С нумерацией остальных многозначных чисел учащихся можно ознакомить в процессе прибавления к многозначным числам, оканчивающимся тремя нулями, чисёл первого класса. На абаке откладывается многозначное число уже известного учащимся вида, например 315 000. На спицы разрядов первого класса нанизываются косточки, соответствующие числу, например 876 (см. рис. 46). Учитель спра4iiивае, как записать число, получившееся в результате сложения 315000 и 876. Ответ очевиден. Подобны числа демонстрируются на нумерационной таблице. Учащиеся учатся называть подобные числа: сначала называется число единиц второго класса, а затем первого класса. Таким образом, число 315 876 читается так: триста пятнадцать тысяч восемьсот семьдесят шесть. Предлагаются и обратные упражнения: по названию числа выполнить его запись (возможно, с предварительным изображением его на абаке). В связи с введением понятия класса в систему упражнений по отработке навыков устной и письменной нумерации целесообразно включать упражнения, требующие использования этого понятия. Это могут быть, например, такие Задания: «Запишите (изобразите на своем абаке) число, в котором: 200 единиц первого класса и 60 единиц второго класса; 107 единиц класса единиц и б единиц класса тысяч; по две единицы в разряде десятков второго класса и в разряде сотен первого класса; 320 единиц класса тысяч и 2 единицы класса единиц» и т. д. Наряду с такими упражнениями предлагаются и обратные: «Назови, к какому классу и разряду относится каждая цифра числа 356 789, 50 283 и т. д.». Изучая нумерацию, учащиеся продолжают упражняться в устных вычислениях (сложении и вычитании) на множестве многозначных чисел: 350 000+102, 200 018+600 100, 85007—80007, 150 120—50 100 и т. д. Для расширенного множества чисел устанавливается справедливость отношения порядка. Учащиеся считают в прямом и обратном порядке, начиная с определенного числа; определяют числа, следующие непосредственно до и после данного числа. Например, им предлагается продолжить счет с 998 до 1005, с 7 589 до 7 600; присчитывать по единице к числам 99 989, 999 997; отсчитывать по одному от чисел 600000, 100000, 10000, 7000; назвать число, которое на 2 меньше, чем 40 000, и т. д. Школьники должны научиться сравнивать многозначные числа. С помощью позиционной таблицы легко показать, что начинать сравнивать два многозначных числа нужно с единиц второго класса. То число больше, у которого больше единиц второго класса. Если их число одинаково, то сравнивается число единиц первого класса. Увеличение и уменьшение числавi0, IОО и IООО раз. Расширяя знания учащихся о десятичной системе счисления, можно ознакомить их с простым способом увеличения или уменьшения числа в 10, 100 и 1 000 раз, кратного сравнения чисел особого вида. Это необходимо для прочного усвоения ими позиционного принципа нумерации. Изложим методику изучения этого материала. Учащимся предлагают рассмотреть ряд чисел и рассказать об их особенностях. Пусть этот ряд имеет вид: 3, 30, 300, 3 000, 30 000, 300 000. В числе обнаруженных особенностей могут быть такие: в каждом числе встречается цифра 3; все числа записаны с помощью одной цифры З или цифры З и нулей; цифра З в каждом числе обозначает разные разрядные единицы: единицы, десятки, сотни и т. д.

Предлагается последовательно сравнить эти числа парами.

Зи 30: ЗОн 10 раз больше, чем З, так как 30:3= 10 (это учащимся известно из темы «Увеличение и уменьшение числа в несколько раз»);

ЗО и ЗОО: эти числа можно представить в виде З десятка и ЗО десятков; это позволит, как и в предыдущем случае, установить, что ЗО десятков в 10 раз больше, чем З десятка, а значит, ЗОО в 10 раз больше, чем ЗО.

Аналогично устанавливается соотношение между парами ЗОО и

3 000, 3 000 и 30 000, 30 000 и 300 000.

далее сравниваются числа З и 300. Случай 300:3 рассматривался

уже в концентре «Тысяча» — 300:3 = 100. А это,

как известно, означает, что 300 в 100. раз больше, чем З. Такие же

соотношения устанавливаются и для чисел ЗО и 3 000, 300 и 30 000,

3 000 и 300 000 (для этого они приводятся к виду З дес. и 300 дес.,

З сот. и 300 сот. и т. д.).

Вывод о том, что 3 000 в 1 000 раз больше, чем 3, делается по индукции. Этот вывод распространяется и на другие пары чисел.

Затем следует обобщение: число, которое в 10 (100, 1 000) раз больше другого, имеет на один (два, три) нуль справа больше. На основании этого вывода делается заключение, что если у числа на один

(два, три) нуль справа меньше, чем у другого числа, то оно в 10 (100 или 1 000) раз меньше другого числа.

Выполняются упражнения на закрепление: «Увеличь число 5 в 10, 100, 1 000 раз; число 80 — в 10, 100, 1 000 раз» и т. д.; «Уменьши

число 300 в 10, 100 раз; число 70000 в 10, 100, 1 000 раз» и т. д. Эти правила без каких-либо пояснений можно использовать для

сравнения чисел 118 и 1180, 27 и 27000 и т. д.

Состав многозначных чисел. С целью подготовки учащихся к изучению алгоритмов письменного умножения и деления полезно научить их определять, сколько полных десятков, сотен,

тысяч содержится в данном многозначном числе.

Ученики обладают некоторым опытом выполнения заданий такого рода: они умеют определять, сколько десятков в трехзначном чис- ле. Это и используется в работе с многозначными числами.

Школьникам предлагается определить, сколько десятков в числе 3 576. Это число представляетсй в виде суммы разрядных слагаемых.

7 Последовательно выясняется, сколько десятков в каждом из

60 этих слагаемых: 7, 50, 300. (Например, учащиеся рассуждают так; в 1000—10 сотен или 100 десятков, значит, в 3000----З00 десятков.) В числе 3 576—357 десятков. Аналогично устанавливается, что в этом числе 35 сотен. Если рассмотреть столь же

подробно еще несколько чисел, то нетрудно заметить закономерность в определении состава числа.

И ме н о в а н н ы е ч ис л а. Большую помощь при изучении и усвоении нумерации многозначных чисел оказывают упражнения с составными именованными числами, выраженными в десятичных мерах. Эти числа дают возможность наглядно представить понятия разряда тысяч, десятков и сотен тысяч. Такие упражнения должны использоваться на всех этапах изучения нумерации. Например, когда учащиеся учатся определять состав многозначного числа, целесообразно выполнить такие упражнения: «Сколько дециметров в 3 576 см? Сколько километров составляют 3 576 м? Сколько килограммов в 12 070 г? Сколько рублей составляют 67 000 к?» и т. д. Основные положения методики обучения нумерации в пределах миллиона могут быть использованы и для знакомства учащихся с числами класса миллионов.

Сложение и вычитание (письменные вычисления). При изучении многозначных чисел учащиеся устно складывают и вычитают числа особого вида, используя знание разрядного состава чисел, т. е. многозначных чисел, которые можно представить в виде двузначных и трехзначных именованных чисел (38 000 + 27 000 — 38 тыс. + 27 тыс., 620 000 — 370 000 — 62 дес. тыс.— 37 дес. тыс, и т. д.). Перед тем как обратиться к приемам письменного сложения и вычитания, ученикам целесообразно поупражняться в решении таких примеров. Алгоритмы письменного сложения и вычитания одинаковы и когда компоненты являются трехзначными числами, и когда они — многозначные числа. Правда, если уменьшаемое и вычитаемое — трехзначные числа, то приходится образовывать или дробить разрядные единицы не более двух раз. Если же компоненты — многозначные числа, то эти операции могут использоваться большее число раз. Поэтому задача учителя состоит в том, чтобы показать учащимся, что известные алгоритмы письменного сложения и вычитания применимы к числам нового вида. Это можно сделать по-разному.

Например, учитель предлагает учащимся систему последователь но усложняющихся сумм и разностей:

Объяснить учащимся, как вычисляются эти примеры, легко, поскольку в каждом случае компоненты можно представить как трехзначные именованные числа, например 756 тыс. + 243 тыс.

Затем ученики складывают и вычитают числа, которые не оканчиваются нулями, но без перехода через десяток и без дробления разрядных единиц.

Перед тем как приступить к изучению более сложных случаев (с образованием новых разрядных единиц и дроблением разрядных единиц на более мелкие), полезно упражнение учащихся в многократном выполнении этих операций.

Например, рассматривается случай прибавления единицы к числу 99 999. Учащиеся знают, что за этим числом следует число 100 000. Однако на абаке или нумерационной таблице подробно рассматривается механизм образования суммы: к 9 единицам прибавить один, получим десяток; в разряд единиц записываем 0, а получившийся десяток прибавляем к 9 десяткам; получаем 10 десятков, или 100; в разряд десятков записываем О и т. д.

Так же подробно можно проследить процесс вычитания единицы из числа 100 000. При этом в записи используются обычные обозначения заема и распределения разрядных единиц (точки и девятки):

При вычислении суммы или разности более высокого уровня сложности от учащихся следует требовать подробных пояснений к выполняемым промежуточным операциям. Например, вычисление разности одного из самых сложных видов — 600 007 — 532 468 учащихся сопровождают следующими объяснениями: «От 7 отнять 8 нельзя. Занять единицы можно только в разряде сотен тысяч. Возьмем одну сотню тысяч (поставим над б точку) и раздробим ее на 10 десятков тысяч. Возьмем десяток тысяч (над разрядом единиц тысяч запишем 9) и раздробим ее на 10 сотен...» и т. д. Соответствующая запись имеет вид:

В дальнейшем время от времени от учащихся требуются краткие комментарии к выполняемым операциям.

Приемы письменного выполнения действий с многозначными числами в основном не отличаются от приемов выполнения этих действий над трехзначными числами. Однако учитель должен иметь в виду, что обилие промежуточных операций может на первых порах вызвать у учеников затруднения. Поэтому при необходимости эти приемы следует проиллюстрировать на абаке.

Сложение и вычитание именованных чисел. Важную роль в теме «Сложение и вычитание многозначных чисел» играют составные именованные числа. Здесь можно использовать опыт работы с такими числами, приобретенный учащимися в концентре <Тысяча». Отметим только, что в дальнейшем особую роль могут играть упражнения с составными именованными числами, выраженными в единицах времени. Они позволят проверить уровень понимания учащимися сути приемов письменного сложения и вычитания. В самом деле, эти приемы будут использоваться в принципиально новых условиях (компоненты выражены в недесятичной системе счисления):

Умножение. На практике письменное умножение и деление изучаются во взаимосвязи. В самом деле, изучение алгоритма письменного умножения на однозначное число открывает возможности для изучения приема письменного деления на однозначный делитель. То же можно сказать и об умножении и делении на двузначные и трехзначные числа. Здесь для удобства методика письменного умножения будет рассматриваться отдельно. Прежде чем обратиться непосредственно к методике обучения учащихся умножению в столбик, выполним дидактический анализ соответствующего алгоритма.

Начнем с конечного результата изучения умножения: учащиеся должны уметь умножать многозначные числа на трехзначные. На конкретном примере вспомним, в чем состоит это умение.

Вначале оба множителя правильно записываются друг под другом. Затем число, стоящее в разряде единиц второго множителя, умножается на многозначный множитель,

начиная с наименьшего разряда. Полученный результат правильно записывается под чертой, отделяющей множители от произведения.

На многозначный множитель умножаются единицы разряда десятков второго множителя. Результат правильно записывается под первым неполным произведением. Наконец, на многозначное число умножаются единицы разряда сотен второго множителя, а результат правильно записывается под вторым неполным произведением. Полученные неполные произведения складываются. Сумма и есть значение произведения 4 345 и 276.

Пока оставим вопрос о том, что значит правильно выполнять записи при умножении в столбик. Очевидно, что расположение записей сказывается на правильности получаемого результата. Выделим только те операции алгоритма, которые связаны с выполнением арифметических действий:

1) многозначное число умножается на однозначное;

2) многозначное число умножается на круглые десятки;

3) многозначное число умножается на круглые сотни;

4) три многозначных числа складываются.

Операция 4 известна учащимся из темы «Сложение и вычитание многозначных чисел», поэтому предметом специального изучения должны стать операции 1—3. Остановимся подробнее на их содерж а нии.

Умножение многозначного числа на однозначное имеет много общего с приемом умножения двузначного числа на однозначное:

многозначный множитель представляется в виде суммы разрядных слагаемых, и эта сумма по специальному правилу умножается на однозначный множитель (543 4 = (500 + 40 + 3). 4). Вместе с тем между этими приемами есть и различие. Так, при умножении многозначных чисел сумма разрядных слагаемых может иметь 3, 4, 5 и даже б слагаемых; на однозначное число умножаются круглые сотни, тысячи, десятки и сотни тысяч; полученные многозначные неполные произведения нелегко сложить в уме.

Итак, для усвоения операции 1 учащиеся должны научиться умножать на число сумму, состоящую из 3,4, 5 и б слагаемых, и умножать на однозначное число многозначные разрядные числа.

Чтобы научить учащихся выполнять операцию 2, нужно либо придумать наглядную иллюстрацию умножения числа на круглые десятки, либо свести этот случай к ранее изученным с помощью специального приема. Второй путь проще. В самом деле, при изучении нумерации многозначных чисел было показано, как увеличить (уменьшить) число в 10, 100 и 1 000 раз. Круглые десятки (сотни) можно представить в виде произведения однозначного числа на 10. Таким образом, выражение 543. 30 можно представить в виде 543 . (3. 10). Для того чтобы учащиеся могли выполнить такое ум ножение, им нужно показать, что умножить число на произведение можно разными способами (в частности, 543 3. 10). Для умножения 543 на З используется операция 1.

Аналогично можно обучить учащихся выполнению операции 3. Итак, разработана стратегия обучения учащихся алгоритму умножения в столбик. Она состоит в последовательном изучении следующих тем.

1. Обобщение правила умножения суммы на число для случаев, когда сумма имеет более двух слагаемых.

2. Умножение разрядных чисел второго класса на однозначное число.

3. Умножение многозначного числа на однозначное.

4. Правило умножения числа на произведение.

5. Умножение многозначного числа на круглые десятки и сотни.

6. Умножение многозначного числа на двузначное.

7. Умножение многозначного числа на трехзначное.

Рассмотрим методику изучения этих тем.

Правило умножения суммы на число. Учащимся предлагается следующая задача: «Для уроков труда было куплено З набора. В каждый набор входила линейка ценой 25 к., угольник за 20 к., циркуль ценой 22 к. и набор фломастеров за З р. Сколько стоили купленные наборы?»

По задаче составляется выражение: (25 + 20 + 22 + 300). 3. Обсуждаются способы вычисления этого произведения: «Если сначала найти стоимость одного комплекта, то получится трехзначное число 367, которое умножить на З трудно. Ответ можно найти и по-другому:

«Узнаем, сколько стоят в отдельности линейки, циркули, угольники и фломастеры. Полученные стоимости сложим. Значит, нужно найти значение выражения: 25 3 + 20 3 + 22 3 + 300. 3». Каждое из произведений учащиеся в состоянии вычислить устно, сумма 900 + + 67 также находится устно. При решении такой задачи у учащихся не должно возникнуть вопроса о правомерности умножения суммы четырех слагаемых на число почленно. Рассматриваемая в задаче ситуация проста и естественна. При необходимости можно рассмотреть аналогичную задачу, в которой на число умножается сумма, состоящая из З или 5 слагаемых. В заключение можно сформулировать правило умножения числа на сумму, однако требовать от учеников его запоминания не следует.

Прием умножения суммы на число закрепляется при выполнении следующих упражнений: «Представь число 183 в виде суммы двух (трех) слагаемых, чтобы его легко можно было умножить на 5» и т. д.; «Умножь удобным способом: (300 + 40 + б) 3, (200 + 70 + +6)5» и т. д.

Умножение разрядных чисел на однозначное число двузначные и трехзначные разрядные числа в пределах тысячи учащиеся умножать умеют. В более сложных случаях — умножение многозначного разрядного числа используется прием замены многозначного множителя однозначным именованным числом.

Вначале школьники вспоминают, как, например, ЗОО умножается на З: «ЗОО—это З сотни, а З сот..З=9 сот. Значит, 300.3= = 900». Этот прием обобщается для случаев 3 000 3, 5 000. 6, ЗОО . 8, 900 . 9, 20 000 . 7 и т. д. В случае, например, 20 000. 7, учащиеся рассуждают так: «20 000 это 2 десятка тысяч; 2 десятка тысяч умножить на 7, получим 14 десятков тысяч, т. е. 140 000». Рас- суждения выполняются учащимися устно, результат записывается.

Умножение многозначного числа на однозначное. Учащиеся могут самостоятельно определить способ умножения многозначного числа на однозначное. Задача учителя состоит в том, чтобы подобрать систему произведений, расположенных по возрастающей сложности.

Самый простой случай, когда неполные произведения являются разрядными числами:

1 232.3 =(1 000 + 200 + ЗО + 2). 3 = 1 000.3 + 200.3 +

30.3+2.3=3000+600+90+6=3696;

20341 .2 =(20 000 + 300+40 + 1). 2 = 20000.2 + 300.2 +

+40.2+1 .2=4Об82

При решении уже второго, третьего примеров такого рода учащимся предлагается выполнять промежуточные действия в уме и записывать сразу ответ.

В более сложных случаях (112053 3, 7083 . 2) целесообразно все вычисления производить с подробной записью промежуточных операций. Особенность этих примеров в том, что неполные произведения учащиеся в состоянии сложить в уме.

Наконец, рассматриваются самые сложные случаи: 2 345 3,

6189 . 2, 7 542 . 7 и и. д. Чтобы вычислить эти произведения в уме,

можно найти значения неполных произведений. Сумма этих произведений вычисляется в столбик. Пусть, например, умножается

64 579 . 4. Учащиеся записывают:

64579.4 = 240 000 + 16000 + 2000 + 280 + 36.

Затем эти числа складываются в столбик:

1

Возможно, достаточно рассмотреть одно-два таких произведения, чтобы учащиеся почувствовали трудоемкость такого алгоритма умножения. Так создается психологическая предпосылка к изучению алгоритма умножения в столбик.

Умно жен и е в столбик. Для обучения учащихся умножению в столбик целесообразно использовать методику, которую можно назвать «обучение по образцу». При этом учитель на конкретных примерах показывает, в чем состоит новый прием, акцентирует внимание учащихся на основных его операциях (пояснениями или графически). Учащиеся под наблюдением учителя воспроизводят этот прием. Обучение по образцу не исключает, конечно, элементов проблемного обучения.

Рассматривается умножение трехзначного числа на однозначное, которое вычислить устно трудно, например 465 7. Учитель записывает множители в столбик, подчеркивая, что однозначный множитель располагается под разрядом единиц первого множителя. На первых порах на доске (в тетрадях) колонки клеток, в которых записаны цифры сомножителей, можно подписывать буквами, обозначающими названия разрядов (рис. 47). Проводится черта, отделяющая сомножители

от произведения, ставится знак умножения «Х ». Затем учитель выполняет на доске умножение в столбик, поясняя свои действия: «Умножаем 5 число единиц в разряде единиц первого множителя на 7. Получаем 35. Записываем цифры этого числа в соответствующие клетки. Умножаем б десятков первого множителя на 7. Получаем 42 десятка (4 — число сотен, 2—-число десятков). Записываем 42 в следующую строчку, располагая цифры в соответствующих клетках; 4 сотни умножаем на 7, получаем 28 сотен (2—число тысяч, а 8 — число сотен в этом неполном

произведении). Записываем его в следующую строчку так, чтобы цифры располагались в соответствующих клетках. Полученные неполные произведения сложим: сначала в сумму запишем 5 единиц, сложим З десятка с двумя и запишем в разряд десятков...»

После этого учитель убеждает учащихся, что выполненное таким образом умножение отличается от ранее рассмотренного способа лишь формой. Поэтому произведение этих же чисел — 465 . 7

вычисляется в строчку:

Если необходимо, рассматривается еще один пример, однако подробные пояснения при этом в основном дают учащиеся.

Учитель предлагает сократить запись умножения в столбик. Это можно сделать, если запоминать некоторые промежуточные результаты, подобно тому как это делалось при сложении и вычитание в столбик. Образец краткой записи уместно показать на уже рассмотренном примере:

Учитель поясняет: «5 умножим на 7, получим 35; 5 записываем под единицами, а З десятка запоминаем; б десятков умножим на 7, получим 42 десятка и еще З десятка — всего 45 десятков; 5 записываем под десятками, а 4 сотни запоминаем; 4 умножим на 7 ...э. В дальнейшем учащиеся все с большей самостоятельностью работают над подобными вычислениями.

Особо следует рассмотреть случаи умножения, когда первый множитель имеет вид: 3 520, 372 400, 872 000 и т. д. При записи этих множителей в столбик приходится умножать однозначный множитель на нуль, причем иногда неоднократно. С помощью уже известного приема показывается, что однозначный множитель умножается не на все разрядные слагаемые, а только на нулевые. Например, вычисляя произведение 872 000 4, на 4 достаточно умножить число 872 и к полученному результату приписать справа три нуля:

В процессе отработки алгоритма умножения на однозначное число используются упражнения с составными именованными числами. Так же как и письменные операции сложения и вычитания, умножение в таких случаях выполняется двумя способами: без перевода единиц величин в более мелкие и с переводом. Первый способ используется для придания конкретного смысла промежуточным операциям алгоритма умножения. Например, при умножении 5 мм на 8 получается 40 мм, что составляет 4 сн; умножение 7 см на 8 дает 56 см, или 5 дм и б см и т. д.

Письменное умножение не должно использоваться учащимися бездумно, применительно к любому произведению многозначного и однозначного чисел. Параллельно с работой над сложными произведениями, которые нельзя вычислить устно, необходимо предусмотреть возможность для упражнения учащихся в устном счете. Для этого в систему упражнений могут включаться, например, такие произведения: 1020.5, 5203.2 и др.

Умножение числа на произведение. При изложении методики обучения учащихся правилам прибавления числа к сумме, суммы к числу и других подчеркивалось, что не следует их побуждать к заучиванию формулировок этих правил. Смысл правил раскрывается через текстовые задачи. Этого же принципа следует придерживаться при обучении учащихся умножению числа на произведение.

В качестве исходной может быть рассмотрена, например, такая содержательная задача, предполагающая практическую деятельность учащихся: «Отрезок длиной 2 клетки тетради нужно увеличить сначала в 3, а потом в 4 раза. Какую длину будет иметь полученный отрезок? Запиши выражение, выполни рисунок». Выясняется, что требуемый отрезок можно построить разными способами (рис. 48):

1) 2 . З . 4 строится отрезок в З раза больший данного, а затем полученный отрезок откладывается на прямой 4 раза (так, чтобы конец предыдущего совпадал с началом следующего);

2) 2.4.3 данный ‚отрезок откладывается на прямой 4 раза,

/ а затем полученный отрезок откладывается З раза;

3) 2 12 данный отрезок откладывается на прямой 12 раз.

Констатируется, что результат выполнения задания разными способами одинаков. Делается вывод, что (2 . 3) 4 = (2 . 4. 3 = = 2 . (4 . 3), т. е. произведение трех чисел можно вычислять в любом порядке.

Это правило иллюстрируется на примерах: «Вычисли произведение удобным способом: 16.5.2,20526, 13. 400.3, ...э Имея ввиду следующую тему, целесообразно решить несколько примеров такого вида: «Вычисли удобным способом: 26.2. 10, 10.4.23, 5•100• 16» и т. д.

Умножение многозначного числа на разрядные ч и с л а. Прежде всего с учащимися нужно вспомнить (во время устного счета, например), как умножить число на 10, 100 и 1000.

Затем в порядке возрастающей трудности предлагаются произведения, в которых один из множителей разрядное число (круглые десятки, сотни, единицы тысяч). Вначале алгоритм умножения таких чисел рассматривается подробно. Пусть нужно умножить 17 на 30; 30 это З десятка, т. е. 3. 10. Значит, 17 можно умножить на произведение 17 . (3. 10). Такое умножение можно выполнить разными способами. Если 17 сначала умножить на 10, то число 170 на З умно. жить трудно. Лучше умножить 17 на 3, получим 51. Это число легче умножается на 10, получаем 510.

Находятся еще несколько произведений, для которых вычисления производятся устно (26 20, 13 60, 17 40 и т. д.).

Аналогично выполняются устные вычисления в случаях, когда один из множителей — круглые сотни или единицы тысяч:

26.200=(26.2). 100=5200

13.600=(13.6)• 100=7800

37 . 2 000 = (37 . 2). 1 000 = = 74 000 и т. д.

Далее рассматриваются сложные случаи, когда устно умножить трудно (216 80, 456 . 400, 78 70, 4 657 . 40 и т. д.). Один из таких примеров решается в строчку:

78.70=(78.7).10=(78).10=5460

Х7

546

Более удобно такие числа умножать сразу в столбик. Так как умножение на 10, 100, 1 000 состоит в приписывании к числу справа

В случаях «а» и «б» учащиеся умеют удобно располагать множители, сносить нули в произведение. По аналогии выполняется запись множителей и в случае «в». В произведение сначала сносятся нули первого множителя (случай «а»), а затем нули второго множителя, (случай «б»). Выполняются упражнения на закрепление этого приема умножения.

Умножение многозначного числа на двузначное. Алгоритм умножения на двузначное число состоит из следующих операций: двузначный множитель представляется в виде суммы разрядных слагаемых; многозначное число умножается сначала на единицы разряда единиц, а затем на второе разрядное число.

Если сравнить алгоритмы умножения на круглые десятки и на двузначные числа, можно заметить между ними сходство:

563.30=563.(3. 10)=...

563.23=563.(2О+3)=...

В некоторых случаях оно еще большее:

267. 12=267.(2+ 10)=

267.20=267.(2. 10)=...

Поэтому можно предположить, что использование правила умножения числа на сумму для объяснения приема умножения на двузначные и трехзначные числа может вызвать у учащихся затруднения. Возможно, целесообразнее другой подход.

Пусть, например, объяснение умножения на двузначное число начинается с рассмотрения произведения 68. 12. По определению это произведение означает сумму из 12 слагаемых, каждое из которых

68. Как вычислить значение такой суммы? Могут быть рассмотрены различные способы: 68 4 + 68 8, 68 5 + 68 7, 68 3 + 68 9 и др.

Очевидно, что в приведенных случаях нужно дважды выполнить умножение в столбик и полученные результаты сложить. Только при вычислении суммы 68 . 2 + 68. 10 умножение в столбик нужно выполнить один раз: 68 2, 68 умножается на 10 устно. делается вывод:

чтобы умножить 68 на 12, удобно умножить на 10, 68 на 2 и полученные неполные произведения сложить в столбик. Этот вывод закрепляется при рассмотрении более сложного случая. Например, 68 35

сумму из 35 слагаемых — удобнее вычислить так: найти сумму ЗО слагаемых 68. 30; найти сумму 5 слагаемых 68 . 5; неполные произведения сложить.

Констатируется, что для умножения данного числа на двузначное нужно умножить данное число на десятки двузначного множителя, а затем на единицы. Вычисляя такие произведения в три приема, учащиеся убеждаются в трудоемкости работы:

далее используется методика обучения по образцу. Учитель записывает на доске более короткий вариант умножения на двузначное число.

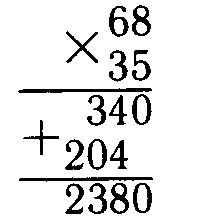
68 Записи сопровождаются пояснениями: «Второй множитель записывается под первым так, чтобы разряды единиц 340 и десятков одного числа находить под соответствующие 204 ми разрядами другого. Умножаем 68 на 5, получаем первое неполное произведение 340. Умножаем 68 на 30, т. е.

68 умножаем на 3, но помним, что в результате получаются десятки. Чтобы не забыть об этом, будем записывать второе неполное произведение, начиная с разряда десятков, т. е. под цифрой 4 первого неполного произведения... Второе неполное произведение равно 204. Находим сумму неполных произведений, она равна 2 380».

Вычисление произведений, в которых первый множитель трехзначное или многозначное число, производится аналогично. Поэтому соответствующие примеры включаются в систему упражнений по данной теме без каких-либо разъяснений.

Особо рассматривается только случай, когда многозначный мно- житель оканчивается одним или несколькими нулями (6 700 . 27, 5 480.64, 77900.21 и т. д.). В случае возникновения у учащихся затруднений учитель напоминает им правила записи таких множителей в столбик и снесения нулей в произведение.

Умножение многозначного числа на трехзначное. Знакомство учащихся с этим алгоритмом также происходит с опорой на определение умножения. Что значит, например, умножить 352 на 246? Это значит, что нужно найти сумму 246 слагаемых, каждое из которых 352. Эту сумму легче вычислить так: найти сумму 200 слагаемых (352. 200), сорока слагаемых (352. 40), шести слагаемых (352. 6), полученные результаты сложить, т. е. 352. 246= =352. 200+352 40+352 6.

Учащиеся убеждаются, что значения каждого произведения они умеют вычислять в столбик, так же можно найти и сумму многозначных неполных произведений. Как и при изучении умножения на дву

Одновременно учащиеся упражняются в устном счете, в част:

ности в умножении многозначных чисел на однозначные, двузначные и трехзначные. для устного счета используются простые случаи умножения: 500 .600, 200 .30, 101 .40, 123. 3, 223.30, 323 .200.

При успешном изучении темы можно рассмотреть частные приемы устного умножения: 299 .4, 399. 50, 302 .31, 405. 11 и др. Умножение таких чисел основано на определении умножения. Так, произведение 299 . 4 можно заменить произведением 300 4, которое вычисляется устно. Первый множитель был увеличен на единицу. Поскольку 300 . 4 можно представить как сумму четырех слагаемых, каждое из которых увеличено на единицу, то, чтобы получить исходное произведение, нужно из 1 200 вычесть 4.

Умножение 302 на 31 можно мысленно представить как сумму, состоящую из 31 слагаемого. Удобно 302 . 30 = 9 060, т. е. найти сумму 30 слагаемых. Если к 9 060 прибавить тридцать первое слагаемое — .302, получим исходное произведение.

Деление. Определим, из каких операций состоит алгоритм. письменного деления (в дальнейшем будем называть его «деление углом»). Рассмотрим хорошо известный процесс деления углом на конкретном примере — 616 236:267 (самый сложный случай деления в начальных классах — деление многозначного числа на трехзначное).

Сначала выделяем неполное делимое 616. Подбираем цифру частного. Возможно, придется опробовать несколько цифр, прежде чем установим, что

это цифра 2. Умножаем делитель на 2, получаем

Вычитаем это произведение из неполного делимого. Разность равна 82. дополняем ее следую

Щей цифрой делимого, получаем неполное делимое 822. Подбираем следующую цифру частного — 3. Умножаем делитель на З и полученное произведение вычитаем из 822. дополняем разность следующей

цифрой делимого, получаем 213. Это неполное делимое не делится на 267, поэтому в частном записываем нуль. Сносим еще одну цифру делимого... и т. д. Отметим, что операция определения первого неполного делимого отличается от операции получения последующих неполных делимых.

Алгоритм можно представить в следующем виде:

1) определение первого неполного делимого;

2) определение цифры частного;

3) умножение делителя на подобранное число;

4) вычитание произведения из неполного делимого;

5) если цифра частного подобрана верно, то выполняется следующая операция алгоритма, если нет, повторно выполняются операции 3—5;

6) определяется неполное делимое. Если оно существует, выполняется третья и следующие за ней операции алгоритма. Если неполного делимого нет, деление окончено.

Приведенный алгоритм получен в результате анализа модели деятельности человека, хорошо знакомого с делением углом. Поэтому, возможно, здесь не отражены в явном виде операции, которые выполняются неосознанно. Поскольку этот алгоритм усваивается младшими школьниками, он нуждается в уточнении. Уточнять и дополнять этот алгоритм будем по мере усложнения случаев деления многозначных чисел. Заметим, что не все выделенные операции требуют специального изучения. Так, операция З изучена в теме «Умножение многозначного числа), операция 4 — в теме «Сложение и вычитание в пределах тысячи.

Изучение темы «деление многозначных чисел» естественно начать со случаев, когда делитель — однозначное число.

деление многозначного числа на однозначное (устное). Обучение делению многозначных чисел на однозначные начинается с самых простых случаев, когда каждое разрядное число делимого делится на делитель нацело: 248:2, 468:2, 639:3, 408:4 и т. д. Чтобы вычислить такое частное, не требуется алгоритма деления углом. Устно, начиная со старшего разряда, делятся разряд- ные числа, а получаемые промежуточные результаты записываются в соответствующие разряды частного.

Например, чтобы разделить 9 603 на 3, 9 тысяч делят на 3, получается З тысячи; б сотен делят на 3, получается 2 сотни; О десятков делят на 3, получается О десятков, З единицы делят на 3, получается единица. Таким образом, в частном З тысячи, 2 сотни, О десятков и одна единица. Значит, частное равно 3201.

Методика обучения этому приему следующая. Учащимся хорошо известен прием деления двузначных чисел на однозначные. Частные 36:3, 48:4, 63:3 вычисляются последовательным делением разрядных единиц. Этот прием учитель иллюстрирует на позиционном абаке, например, для частного 69:3 (рис. 49). Выполняется запись: 63:

:3=60:3+3:3. Затем наглядно можно представить прием деления в более сложном случае — 693 069:3. Этот процесс комментируется и описывается: 693069:3=600000:3+90000:3+ 3000.3+60:

:3+9:З2ООООО+ЗОООО+1 000+20+3231 023. Правильность выполнения операции проверяется умножением. Подобные примеры учащиеся в состоянии выполнить без абака и промежуточных записей.

Поскольку рассмотренный прием устного деления многозначного числа на однозначное легко проиллюстрировать, нет необходимости в каких-либо математических обоснованиях (например, «доказательстве > правила деления суммы, состоящей из З и более слагаемых, на число). Излишним было бы и введение здесь специальной терминологии: «неполное делимое», «подбор цифры частного» и т. д., используемой в дальнейшем.

деление многозначного числа на однозначное (письменное). При изучении операции определения первого неполного делимого использует общий прием деления двузначного числа на однозначное. Чтобы вспомнить его, учащимся предлагается найти следующие частные: 81:3, 76:4, 65:5, 84:7, 91:7. Комментируя операцию деления, ученики воспроизводят содержание приема деления двузначного числа на однозначное: «Представим делимое суммой удобных слагаемых: одно из них самое большое число десятков, которое делится на делитель».

Затем рассматриваются более сложные частные. делимые в них — трехзначные числа, позволяющие использовать этот же прием деления: 920:2, 510:3, 840:3 и т. д. для первого частного такого вида преобразования можно выполнить письменно. Эта работа сопровождается, например, такими комментариями:

920:2 =

= (800 + 120):2 = Представим делимое суммой удобных слагаемых, одно из КО

ТОРЫХ — наибольшее число сотен, делящееся на делитель.

=800:2+120:2= делим оба слагаемых на делитель.

= 400 + 60 = 460 Складываем полученные частные. Правильность деления проверяется умножением. :3+9:З2ООООО+ЗОООО+1 000+20+3231 023. Правильность выполнения операции проверяется умножением. Подобные примеры учащиеся в состоянии выполнить без абака и промежуточных записей.

Поскольку рассмотренный прием устного деления многозначного числа на однозначное легко проиллюстрировать, нет необходимости в каких-либо математических обоснованиях (например, «доказательстве > правила деления суммы, состоящей из З и более слагаемых, на число). Излишним было бы и введение здесь специальной терминологии: «неполное делимое», «подбор цифры частного» и т. д., используемой в дальнейшем.

деление многозначного числа на однозначное (письменное). При изучении операции определения первого неполного делимого использует общий прием деления двузначного числа на однозначное. Чтобы вспомнить его, учащимся предагается найти следующие частные: 81:3, 76:4, 65:5, 84:7, 91:7. Комментируя операцию деления, ученики воспроизводят содержание приема деления двузначного числа на однозначное: «Представим делимое суммой удобных слагаемых: одно из них самое большое число десятков, которое делится на делитель».

Затем рассматриваются более сложные частные. делимые в них — трехзначные числа, позволяющие использовать этот же прием деления: 920:2, 510:3, 840:3 и т. д. для первого частного такого вида преобразования можно выполнить письменно. Эта работа сопровождается, например, такими комментариями:

920:2 =

= (800 + 120):2 = Представим делимое суммой удобных слагаемых, одно из КО

ТОРЫХ — наибольшее число сотен, делящееся на делитель.

=800:2+120:2= делим оба слагаемых на делитель.

= 400 + 60 = 460 Складываем полученные частные.

Правильность деления проверяется умножением.

В дальнейшем подобные примеры решаются устно.

После этого учитель приступает к объяснению деления трехзначных чисел.

Рис. дальнейшем подобные примеры решаются устно.

После этого учитель приступает к объяснению деления трехзначных

Приведем вариант пояснений к вычислению первого частного (цифра в скобках указывает порядковый номер операции алгоритма).

(1). Первое неполное делимое — 22.

(2). На 4 можно разделить 20, значит, первая цифра частного 5.

(3). Второе неполное делимое — 22 — 20 = 2, т. е. 2 десятка тысяч, или 20 тысяч, и еще б тысяч — 26.

(2). Из 26 на 4 можно разделить 24, значит, следующая цифра частного — 6.

(3). Найдем следующее неполное делимое — 26 — 24 = 2, осталось разделить 2 тысячи, или 20 сотен, и еще 8 сотен 28.

(2). 28 делится на 4, следующая цифра частного 7.

(3). Следующее неполное делимое — О десятков.

(2). 0 разделим на 4 и запишем в разряд десятков частного 0.

(3). Следующее неполное делимое — О единиц.

(2). 0 разделим на 4 и запишем в разряд единиц частного 0.

Ответ: 56 700.

После вычисления учащиеся могут догадаться», что нули делимого можно просто сносить в частное. В таком случае им предлагается, не выполняя деления, ответить, сколько нулей будет во втором частном (226 800:5). Вычислив это частное, ученики видят, что «догадка > неверна. Учитель объясняет, что для того чтобы не допускать ошибок при делении — не забывать записывать нули в частном и не записывать в частном лишние нули,— нужно заранее определять, сколько цифр имеет частное. Раскрывается содержание этой операции.

Например, для того чтобы узнать, сколько цифр в значении частного 226 800:5, определяется смысл первого неполного делимого. Число 22 означает в делимом десятки тысяч. При делении десятков тысяч в частном получаются десятки тысяч. Такие числа записываются с помощью пяти цифр. Значит, в частном будет пятизначное число. Можно посоветовать учащимся помечать места для цифр частного точками еще до начала деления.

На конкретных примерах ученики убеждаются в том, что определение количества цифр в частном полезно при любом делимом, а не только когда оно оканчивается нулями. Можно рассмотреть следующие частные: 7 371:7, 4 856:8, 45 063:9 и т. д. (Значения этих частных выражаются числом с одним или несколькими нулями в середине.) 4856 8 Пусть, например, 4 856 делится на 8. Первое неполное

56 Г607 делимое — 48, Оно означает количество сотен в делимом, значит, в частном будут получены сотни. Так как количество сотен записывается с помощью трех цифр, то значение частного будет трехзначным.

48:8=6, первая цифра частного—б.

Следующее неполное делимое — 5 десятков. Число 5 на 8 не делится, значит, в частном в разряде десятков нужно записать О (иначе

частном получится двузначное число), и т. д.

В дальнейшем при делении углом после выделения первого неполного делимого всегда выполняется операция определения количества цифр в частном.

Итак, в результате изучения письменного деления многозначного числа на однозначное учащиеся должны усвоить следующий алгоритм деления.

1. Определяется первое неполное делимое. В делимом, начиная со старшего разряда, выбирается такое наименьшее число, которое делится на делитель.

2. Определяется количество цифр в частном. Выясняется, какими разрядными единицами выражено первое неполное делимое. В частном получаются соответствующие разрядные единицы. В нем столько цифр, сколько необходимо для записи числа с данным количеством разрядов.

3. Определяется цифра частного. В неполном делимом выбирается наибольшее число, которое делится на делитель. Выполняется табличное деление.

4. Определяется неполное делимое. Вычисляется, сколько единиц осталось после деления предыдущего неполного делимого. К ним прибавляются единицы следующего разряда.

После операции 4 снова выполняется операция 3, и так до тех пор, пока можно будет образовывать неполные делимые.

Остановимся еще на нескольких методических особенностях изучения темы «Деление многозначного числа на однозначное».

Основой обучения математике в начальных классах являются текстовые задачи. Поэтому и при изучении алгоритма письменного деления учащимся часто приходится встречаться с частными, в которых компоненты представлены именованными и составными именованными числами. Наиболее часто деление в таких случаях выполняется так: сначала компоненты приводятся к одному наименованию, затем выполняется деление над отвлеченными числами: частное представляется в виде именованного или составного именованного числа.

Пусть, например, необходимо найти частное 24 р. 21 к.: З к:

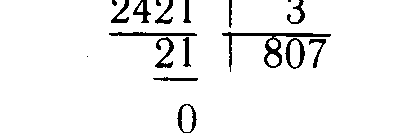
Частное 807 именуется исходя из условия задачи.

Учащимся можно было бы предложить найти значение этого частного без предварительного перевода единиц. В таком случае операции алгоритма деления выполняются в несколько необычной ситуации, что, безусловно, полезно.

При изложении методики обучения делению в концентре <Сотня> отмечалось, что в житейских ситуациях деление с остатком приходится выполнять гораздо чаще, чем без остатка, Поэтому в систему упражнений по отработке приема деления целесообразно включать случаи деления с остатком. Это же требование распространяется и на систему упражнений по совершенствованию навыков деления углом.

Умение выполнять деление с остатком полезно еще в одном отношении. Известно, что при делении на двузначные и трехзначные числа особое значение имеет оценка промежуточных остатков. Если при делении неполного делимого остаток больше делителя, то соответствующая цифра частного подобрана неверно. Так, если при делении числа 345 678 на 7 получился остаток 18, учащихся легко убедить, что деление выполнено неверно: в частном должно получиться пятизначное число. Школьникам напоминается, что остатки при делении на число меньше делителя. Поэтому ошибку, допущенную при делении, можно обнаружить исходя из полученного остатка: 18 больше делителя, значит, 18 не может быть остатком:

Упражнение учащихся в делении с остатком целесообразно и для обобщения приема деления на 10 и 100. Этот прием будет использоваться в дальнейшем, при делении на двузначные и трехзначные числа.

Ученики знают, так разделить числа 80, 150, 1 300, 1 230 на

10; числа 800, 2 400, 75 200 на 100. Рассматриваются частные вида:

83:10, 157:10, 1236:10, 820:100, 824:100, 807:100, 2 415:100 и т. д.

В делимом выделяется наибольшее количество десятков (сотен).

Они делятся на 10(100) по известному правилу. Оставшаяся

часть делимого и составляет остаток.

Например: 83:10=8 (ост. 3) 157:10=15 (ост. 7)

860:100=8 (ост. 60) 571:100=5 (ост. 71)

Умение делить на круглые десятки и сотни используется при подборе цифр частного при двузначном и трехзначном делителе.

Деление многозначного числа на разрядное число. Перейдем к рассмотрению методики обучения учащихся алгоритму деления многозначного числа на двузначное. Алгоритм деления на двузначные числа изучается в два приема. Сначала учащиеся учатся делить многозначное число на круглые десятки и сотни. Умение делить на круглые десятки и сотни используется при подборе цифр частного при двузначном и трехзначном делителе. Учащиеся уже знакомы с приемом деления на 10, 100 и 1 000, знают алгоритм деления на однозначное число. Таким образом, деление на круглые десятки и сотни должно быть сведено к последовательному делению многозначного числа на 10 (100) и на однозначное число. Например, чтобы разделить 4 560 на 50, достаточно разделить 4 560 на 10, а заем456—на5.

Для того чтобы учащиеся могли сознательно использовать этот прием, необходимо им показать, что деление числа на произведение можно выполнить различными способами: а: (Ь . с) (а: Ь): с = =(а:с):Ь.

Отметим, что учитель не должен требовать от учащихся заучивания этого правила — это повлекло бы за собой многочисленные ошибки, связанные с заменой действия умножения делением.

Доста

точно рассмотреть несколько задач, допускающих практическое, хорошо иллюстрируемое решение. Например: отрезок длиной 12 см разделить на б равных частей разными способами. Определить длину полученных частей». Учащиеся выполняют это задание тремя способами: 12:6, 12:3:2, 12:2:3 (рис. 50).

Сложнее в практическом отношении следующая задача: «Разделить прямоугольник площадью 80 клеток (8Х 10) на 40 равных частей. Какой вид будут иметь полученные части?» Она имеет больше вариантов решения — 80:2:20, 80:8:5, 80:4:10.

Затем переходят к изучению приема деления на круглые десятки и сотни.

Сначала рассматриваются частные, значения которых учащиеся находят устно: 210:70, 350:50, 860:20, 480:30 и т. д. Один из примеров можно решить подробно, с записью промежуточных операций: 210:

:70=210:(7. 10)=210:10:7=21:7=3.Востальныхслучаяхученики ограничиваются устными комментариями.

Затем рассматриваются случаи деления на круглые десятки с остатком: 216:70, 186:30, 376:50, 562:40 и т. д. Учитель показывает, как в данных случаях может быть использован прием деления углом. Деление сопровождается, например, такими пояснениями: «Первое

376 70 неполное делимое 376. В частном будет од

350 5 (ост. 26) на цифра. Определим цифру частного: 376

26 разделим на 10, получим 37; 37 разделим на 7

получим 5. Определим, сколько единиц делимого разделили:

70 . 5 = 350. Определим, сколько единиц делимого осталось: 376—

—350=26. Остаток меньше делителя, значит, цифра частного подобрана верно».

Как видно из пояснения, операции 1 и 2 алгоритма деления углом остались неизменными. Операция определёния цифры частного усложнилась.

Наконец, учащиеся переходят к делению многозначных чисел на круглые десятки: 19880:70, 24810:30, 27540:60, 42 150:50 и т. д.

Учитывая сложность этих случаев, записывают промежуточные операции. Операция подбора цифр частного подробно поясняется.

Приведем пример пояснений к определению частного 19 880:70:

<Первое неполное делимое 198. В частном будут З цифры. Определим первую цифру частного: 198 разделим на 10, получим 19; 19 разделим на 7, получим 2. Записываем 2 в частное. Выясним, сколько единиц неполного делимого разделили: 70. 2= 140.

Определим, сколько единиц неполного делимого

осталось: 198— 140= 58. Остаток меньше делите-

ля, значит, цифра частного подобрана верно.

Определим следующее неполное делимое...» и т. д.

Методика изучения приема деления многозначного числа на круглые сотни аналогична.

Сначала рассматриваются случаи деления, когда результат может быть вычислен устно: 4 200:700, 56 000:800, 120 000:300 и т. д. Используется прием: 4200:700=4200:100:7=42:7=6.

В более сложных случаях значение частного находится углом:

Первое неполное делимое 6 785. В частном одна цифра. Определим цифру частного: 6 785 разделим на 100, получим 67; 67 разделим на 8, получим 8. В част-

ном записываем 8. Вычислим, сколько единиц неполного делимого разделили: 800. 8=6 400. Определим, сколько единиц еще осталось разделить: 6 785—6 400= 385. Остаток меньше делителя, значит, цифра частного подобрана верно».

Наконец, выполняется деление многозначных чисел на круглые сотни: 136 500:500, 246 300:300, 658 400:800 и т. д.

Работа над приемами деления на круглые десятки и круглые сотни может проводиться параллельно. В систему упражнений для закрепления навыков деления многозначных чисел на разрядные числа могут включаться примеры на деление с остатком.

деление на двузначные числа. Алгоритм деления на двузначные числа отличается от алгоритма деления на однозначные только процедурой определения цифр в частном. Соответствующая операция отрабатывается при обучении делению на разрядные числа. Однако в таких случаях цифры частного определяются однозначно. Проверка правильности выбора цифр носит условный, исключительно пропедевтический характер. При делении на двузначное число умение определять, верно ли подобрана цифра частного, играет важную роль. В остальном алгоритм деления на двузначные числа не отличается от алгоритма деления многозначных чисел на одно- зна ч ные.

Разъяснение особенностей деления на двузначное число целесообразно начать на примерах частных с трехзначным делимым, когда в частном получается однозначное число.

Учащимся может быть предложен, например, следующий вариант объяснения: «Первое неполное делимое 367. В частном будет однозначное число. Определим цифру частного. Предположим, что делитель - 70, потому что в этом случае мы умеем определять цифру частного: 367 делим на

10, получаем 37; 37 делим на 7, получаем 5. Но 5 — это пробная

цифра, потому что делитель не 70, а 74».

Проверим верно ли определили цифру частного: 74 умножим на 5, получим 370; 370 больше делимого, значит, в частном число меньше 5. Например, 4. Проверим: 74. 4=296, 367—296=71. Остаток 71 меньше делителя, следовательно, частное равно 4».

Как видно из приведенного объяснения, принципиально новым для учащихся является замена делителя числом, в котором цифра в разряде единиц заменяется нулем. Конечно, подбор цифр в частном был бы эффективнее, если бы делитель округлялся. Однако округление — это алгоритм. Так как алгоритм деления непрост, усложнять его дополнительной операцией нецелесообразно.

На первых порах, для «облегчения) проверки пробных цифр частного, можно предложить учащимся записывать произведение пробного числа на делитель карандашом. С приобретением опыта устного умножения и сравнения неполного делимого с произведением потребность в записях карандашом отпадет. Многое здесь зависит от индивидуальных особенностей учащихся: некоторым ученикам можно разрешить с самого начала обходиться без карандаша, другие могут пользоваться им достаточно долгое время.

далее алгоритм деления используется в более сложных случаях, когда делимое — многозначное число, оканчивающееся нулями, или / частное содержит нули в середине.

Приведем пример рассуждений (достаточно подробных), которыми ученики сопровождают операцию деления многозначного числа на двузначное в одном из самых трудных случаев,

когда делимое оканчивается нулем и в частном есть нуль в середине. В скобках указан номер выполняемых операций алгоритма деления.

(1). Первое неполное делимое—2б3.

(2). В частном будут 4 цифры.

(3). 263 разделим на 20: 263 разделим на 10, получим 26; 26 разделим на 2, получим 13. Но в разряд тысяч частного можно записать только однозначное число, следовательно, это будет самое большое

однозначное число — 9.

(4). 28 умножим на 9, получим 252.

(5). Из неполного делимого вычтем это произведение, получим 11.

(6). Разность больше делителя, значит, число тысяч в частном определили верно.

(7). Следующее неполное делимое— 113.

(3). Разделим 113 на 20: 113 разделим на 10, получим 11; 11 разделим на 2, получим 5. Проверим эту цифру.

(4). 28 умножим на 5, получим 140.

(5). Значит, число в разряде сотен частного определено неверно.

(3). Возьмем меньшую пробную цифру 4.

(4). 28 умножим на 4, получим 112.

(5). От 113 отнимем 112, получим 1.

(6). Остаток меньше делителя, следовательно, в частном в разряде сотен цифра 4.

(7). Следующее неполное делимое 14 (десятков).

(3). 14 разделим на 28, получим О десятков.

Операции 4—6 не выполняются, так как правильность подобрав- ной цифры частного очевидна.

(7), Следующее неполное делимое 140 и т. д.

Деление на трехзначные числа. Отметим, что программой 1986 г. не предусмотрено обучение младших школьников делению многозначных чисел на трехзначные. Однако вполне допустимо и методически целесообразно рассмотреть с учащимися деление не только на трехзначные, но и на четырех- и пятизначные числа. С одной стороны, это поможет им увидеть широкие возможности использования изученного алгоритма, с другой — способность учащихся самостоятельно реализовать алгоритм в новых условиях свидетельствует о высоком уровне соответствующих навыков.

Алгоритм деления на трехзначное число отличается от алгоритма деления на двузначное только операцией подбора цифр частного.

Учащиеся знакомы с делением многозначных чисел на круглые сотни, им также известен прием подбора цифры частного, если делитель двузначное число. С учетом этого вводится прием подбора цифр частного, когда делитель — трехзначное число. Суть его в следующем: цифры разрядов десятков и единиц в делителе заменяются нулями (например, если делитель 326, то он заменяется числом 300). Неполное делимое делится сначала на 100, а затем на число сотен в делителе.

Приведем фрагменты пояснений, которыми

учитель сопровождает демонстрацию алгоритма

деления на трехзначное число.

«...Определим цифру сотен в частном: 1069

разделим на 100, получим 10; 10 разделим на 3,

получим 3. Проверим, подходит ли эта пробная

цифра: 365 умножим на 3, получим 1095 --- про

изведение больше делимого, значит, цифра З не подходит. Пробуем число, меньшее, чем 3, т. е. 2...».

е...Определим цифру в разряде десятков частного: 3 394 разделим на 100, получим 33; 33 разделим на 3, получим 11. Следовательно, пробная цифра частного — 9...»

Материал для вычислений учащиеся в основном получают из задач. Поэтому действие деления им часто приходится выполнять над именованными и составными именованными числами. В этих случаях оба компонента приводятся к общему наименованию, деление выполняется так же, как над отвлеченными числами.

Вопросы и задания для самостоятельной работы:

К § 14

1. Почему изучению концентра десяток предшествует подготовительный этап? Какие методические задачи должны решаться на этом этапе?

2. Опишите содержание какой-либо системы упражнений, предлагаемой учащимся на подготовительном этапе.

3. Какими знаниями и умениями должны владеть учащиеся после изучения концентра десяток?

4. Приведите примеры упражнений, с помощью которых раскрывается смысл отношений больше», меньше, равно» на множестве чисел первого десятка.

К § 15

5. В чем состоят особенности методики изучения нумёрации чисел второго десятка?

7. Каким условиям должна удовлетворять методика обучения учащихся приемам устного сложения и вычитания?

8. Опишите устройство абака и принципы работы с ним.

9. Проведите логико-дидактический анализ приемов устного сложения в пределах ста.

10. Проведите логико-дидактический анализ приемов устного вычитания в пределах ста.

11. Раскройте общую идею формирования у учащихся понятия операции умножения.

12. Кратко сформулируйте основные положения методики обучения учащихся табличному умножению (делению).

13. Какие случаи умножения и деления относятся к внетабличным? Какова последовательность их изучения? Опишите методические особенности каждого из них.

К * 16

14. Как устроен позиционный абак? Опишите методику его использования для обучения учащихся нумерации чисел в концентре Тысяча.

15. Какие случаи сложения и вычитания, умножения и деления в концентре Тысяча относятся к устным? Объясните почему.

16. Расскажите, как с помощью абака разъяснить учащимся сущность приемов письменного сложения и вычитания.

К § 17

17. Какие новые сведения о позиционной системе счисления получают учащиеся в концентре многозначные числа?

18. Кратко опишите существенные элементы методики изучения нумерации многозначных чисел.

19. По какому плану изучается прием письменного умножения?

20. Раскройте содержание методики обучения учащихся письменному умножению многозначного числа на однозначное и двузначное число.

21. Какие этапы можно выделить в методике обучения учащихся приему письменного деления? Объясните почему.

22. Раскройте содержание методики обучения учащихся письменному делению многозначного числа на однозначное и двузначное число.

У. ОБУЧЕНИЕ УЧАЩИХСЯ РЕШЕНИЮ ТЕКСТОВЫХ АРИФМЕТИЧЕСКИХ ЗАДАЧ 18. АРИФМЕТИЧЕСКИЕ ЗАДАЧИ В НАЧАЛЬНОМ КУРСЕ МАТЕМАТИКИ Под текстовыми арифметическими задачами подразумевают задачи, имеющие житейское, физическое содержание и решаемые с помощью арифметических действий. Эти задачи занимают в начальном курсе математики важное место. Включение арифметических задач в программу по математике для ‘—‚У классов обусловлено следующими причинами. 1. Используемые в текстовых задачах житейские понятия и представления являются исходным материалом для формирования у учащихся первоначальных абстракций и математических понятий. С другой стороны, такие задачи позволяют учащимся видеть за математическими понятиями и отношениями вполне реальные, жизненные явления. 2. Обучая учащихся решению задач определенных типов, учитель имеет возможность формировать у них общие методы решения математических задач, определенный круг умственных умений и логических операций. З. Арифметические задачи выполняют воспитательные функции: учащиеся знакомятся с явлениями окружающей действительности, имеющими важное мировоззренческое значение и являющимися ос- новой для формирования моральных качеств. Рассмотрим некоторые методические следствия из этих общих положений. Первая из выделенных причин является основанием для классификации большей части задач. В самом деле, поскольку математические понятия, предусмотренные программой, вводятся посредством арифметических задач, то каждому из них соответствует определенный тип задач. Эта же причина определяет и специфику обучения решению арифметических задач в начальной школе. решения текстовой задачи состоит в том, что решаются, вообще говоря, две разные, хотя и взаимосвязанные проблемы: перевод содержания задачи на математический язык (т. е. математизация содержания) и решение собственно математической задачи средствами математики. (Мы сознательно не упомянули еще один аспект процесса решения текстовой задачи «перевод> результата решения математической задачи на содержательный язык условия. В начальной школе это не требует, как правило, специальных навыков.) Проиллюстрируем сказанное на примерах. Задача 7. В колхозе с 30 га собрали 68 т ржи. Урожайность картофеля в этом колхозе оказалась в б раз большей, чем урожайность ржи. Определить урожайность картофеля. для ученика IУ класса не составит труда математизировать содержание данной задачи: урожайность определяется делением уроая на соответствующую площадь 68:30; полученную урожайность ржи нужно увеличить в б раз, следовательно, математическое содержание данной задачи представляется в виде выражения — 8:30- 6. Найти же значение этого выражения ученик IУ класса не :может, так как для этого у него недостаточно математических знаний. Задача 8. В школьном зале стоят скамьи. Если всех учащихся школы рассадить по 7 чел. на каждую скамью, то на одной окажется только 5 чел. Если же на каждую скамью посадить по 5 чел., то 38 учеников останутся без места. Сколько скамеек было в зале? Эту задачу можно решить с помощью выражения 38:(7—5)+I. очевидно, что найти его значение не составляет труда для ученика [II класса. Однако прийти к выражению в результате математизации содержания данной задачи сможет не всякий старшеклассник. Таким образом, проблемы математизации и вычисления ответа задачи разные не только по содержанию, но и по сложности. ‘ Особенность обучения решению задач в младших ‘классах состоит в том, что основные усилия учителя должны концентрироваться меню на обучении математизации содержания текстовых задач навыки вычислений гораздо экономнее (по времени): формировать и отрабатывать при решении числовых примеров. Так, при решении задач: Миши З марки, а у Сергея 5. Сколько марок у обоих мальчиков вместе? .к У Миши З марки, а у Сергея Iа 5 марок больше. Сколько марок у Сергея? учитель должен показать, что математическое содержание этих разных задач выражается умной. Вычисление значения этой суммы — второстепенная проблема. Задача формирования у учащихся общих методов решения математических задач является одной из самых важных и сложных. наиболее фундаментальные исследования в этой области были предприняты д. Пойа’. Обучёнию ‚решению задач учащихся средних и старших классов посвящены работы А. Б. Василевского, Л. М. Фридкана**. Естественно, что в начальных классах у учащихся должны формироваться определенные общие приемы решения математических задач, которые получат дальнейшее развитие в средних и старших Классах. К ним можно отнести: анализ текста задачи (выделение условия и требования, расчленение условия на отдельные данные); выполнение схем, чертежей, иллюстраций по условию задачи; поиск решения задачи с помощью аналитико-синтетического метода; проверку решения задачи. Воспитательная функция обучения математике в начальных классом. его книги: Как решать задачу—М.: Учпедгиз, 1961; Математическое отрьттие.Ь . М.: Наука, 1970; Математика и правдоподобные рассуждения.— М.: Нау. а, 1975. ** Василевский А. Б. Методы решения задач.— Мн.: Выш. шк., 1974; Василевкий А. Б. Обучение решению задач.— Мн.: Выш. цiк., 1979; Фридман Л. М., Турецсий Е. Н. Как научиться решать задачи.— М.: Просвещение, 1984.

сах в значительной степени реализуется через сюжеты арифметических задач. В них на конкретном числовом материале показана экономическая мощь нашего государства, его достижения в области науки и культуры. Соответствующие данные могут быть почерпнуты учителем из сборников ЦСУ СССР и союзных республик, периодической печати. - Решая арифметические задачи, учащиеся знакомятся с понятиями, имеющими важное значение в повседневной жизни, такими, как урожайность, выработка, плановое задание, цена, стоимость и др., усваивают некоторые физические понятия: скорость, масса, объем время. 19. ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ОБУЧЕНИЯ УЧАЩИХСЯ РЕШЕНИЮ ЗАДАЧ с Общие положения. В процессе решения текстовых арифметических задач различных типов у учащихся начальной школы должны г’ вырабатываться общие приемы решения задач. С этой целью учитель т организует работу над задачей, как правило, по одному и тому же я плану. Накапливая опыт такой работы, ученики все с большей степенью самостоятельности применяют соответствующие умения. Рассмотрим возможный план работы учащихся над арифметической задачей: 1) анализ текста задачи; 2) схематическая запись условия; у 3) поиск решения задачи; составление плана решения; и 4) решение собственно математической задачи — вычисление значения числового выражения; 5) истолкование результата вычислений, т. е. получение ответа ц на вопрос задачи; 6) проверка полученного ответа. Этот план может существенно изменяться, если задача решается устно или составлена по иллюстрации. а В методической литературе встречаются и другие варианты, который принципиально не отличаются от данного. Рассмотрим содержание и методику работы учителя на наиболее сложных и важных этапах решения задачи, т. е. на 1—3-м и 6-м этак пах. Относительно 4-го и 5-го этапов отметим следующее. Успешность п работы учащихся на 4-м этапе зависит не от умения решать задачи, а т от уровня сформированности у них вычислительных навыков. Эти с навыки совершенствуются при выполнении учениками специальных а упражнений. При решении задач школьникам, конечно, приходится определять смысл числа, полученного в результате вычислений. Однако это не составляет методической проблемы, поскольку текстовые задачи для 1—iУ классов имеют относительно простую структуру. Анализ текста задачи — многоцелевая работа. Во-первых, перед 1 тем как приступить к решению задачи, учащийся должен усвоить условие Задачи. А это для него не просто, так как в тексте задачи может содержаться З и более предложений. Поэтому цель анализа текста — усвоение содержания задачи. 160

Во-вторых, в процессе анализа текста ученик должен выделить условие и требование задачи. Это тоже не всегда просто, даже если задача решается в одно действие. Например: «Наташе 4 года. Сколько лет Сереже, если он на 2 года старше Наташи?»; «Сколько молока можно доставить в З флягах, если вместимость каждой из них —35 л?» В-третьих, в условии задачи необходимо выделить все данные, которые можно «перевести» на язык математики. При этом также могут возникнуть трудности. Пусть, например, анализируется условие задачи: «Из двух городов, расстояние между которыми 390 км, одновременно навстречу друг другу выехали два автомобиля. Скорость одного 60 км в час, другого — 70 км в час. Какое расстояние до встречи проехал каждый автомобиль?» В условии этой задачи необходимо выделить не только «очевидные» данные — «расстояние между породами 390 км», «скорость одного автомобиля 60 км в час», «скорость другого автомобиля 70 км в час», но и то, что автомобилТ1 находились в пути до встречи одинаковое время. Последнее «зашифровано» в условии: выехали «одновременно» и ехали «до встречи». Иногда требование задачи представляет собой конъюнкцию требований. В таких случаях необходим анализ требования задачи. Например, в задаче: «Расстояние от Москвы до Ленинграда 950 км. Из Москвы в Ленинград вышел поезд со скоростью 85 км в час и через 2 ч прибыл в Калинин. На каком расстоянии от Москвы и Ленинграда находится Калинин?» вопрос содержит два требования: найти расстояние от Москвы до Калинина и от Калинина до Ленинграда. Возможны различные варианты организации работы учащихся над текстом задачи. Это зависит от того, умеют ли учащиеся читать, принадлежит ли данная задача новому типу, в какой степени школьники владеют навыками анализа текста. Приведем фрагмент работы над текстом приведенной выше зада1 чи. Она организована в виде фронтального опроса. Предварительно учащиеся самостоятельно прочитали текст задачи. У ч и т е л ь: О чем говорится в задаче? Ученик А.: О том, что из двух городов... У ч и т е л ь: О чем еще говорится в задаче? У ч е н и к Б.: Расстояние между городами 390 км У ч и т е л ь: Что еще известно? У ч е н и к В.: Выехали два автомобиля... Учитель: В каком направлении ехали автомобили? Уч е н и к Г.: Навстречу друг другу... Уч и тел ь: Говорится ли в условии о времени движении автомобилей? Уч е н и к д.: да, известно, что автомобили выехали одновременно... Затем задаются вопросы относительно числовых значений, содержащихся в условии: «Что такое 390 километров?», «Что такое 60 км час? 70 км в час?» В заключение учащимся предлагается сформировать требование задачи. В процессе опроса учитель побуждает к участию в анализе текста дачи как можно больше учащихся и формулирует вопросы таким 5разом, чтобы обратить внимание учащихся на существенные элементы текста, которые составляют условие и требование задачи. Иногда по ходу анализа текста задачи учителю приходится знакомить учащихся с новыми словами, объектами, явлениями, связями между ними. Например, в приведенной выше задаче, если она является одной из первых на встречное движение, учитель должен показать, что одновременное начало движения двух объектов и их встреча в пути означает, что до встречи оба объекта находились в пути одинаковое время. При этом учитель может воспользоваться подвижными моделями. Необходимо также проверить правильность формулировки текста задачи.

Неправильно сформулированная задача не имеет решения. Однако такие задачи время времени полезно предлагать учащимся, поясняя при этом требования к правильной постановке задач. Например: «На озере плавали 4 журавля, а гусей — на 2 больше. Сколько гусей плавало?»; «Сережа сорвал с яблони З яблока, а Наташа — 2 яблока. Сколько яблок было на яблоне?»; «Из двух городов в одном направлении выехали два автомобиля. Один ехал со скоростью 70 км в час, а другой — 60 км в час. Через 4 ч после того как первый автомобиль выехал, он догнал второй. Определить расстояние между городами».

В условии первой задачи содержится ложное утверждение (журавли не плавают), во второй задаче условие логически не связано с требованием, для решения третьей задачи в условии недостаточно данных.

Интерпретация условия задачи. Составление по условию задачи чертежа, схемы, рисунка и т. д., т. е. интерпретация условия задачи (в дальнейшем будем пользоваться именно этим термином) — не самоцель. Она выполняется (учителем, или учащимися под руководством учителя, или самими учащимися в зависимости от их подготовки, от сложности задачи) только тогда, когда ученики не могут решить данную задачу. Рассмотрим несколько видов интерпретации условия. Каждый из них в разной степени помогает ученикам математизировать содержание задачи. Начнем с самого «слабого», предполагающего высокий уровень -умения решать задачи какого-то определенного типа.

Краткая запись условия задач и. Не существует какой- либо определенной формы краткой записи условия. Критерием эффективности краткой записи являются признаки: краткая запись наглядно представляет связи между величинами и соответствующими числовыми данными задачи; по ней ученик способен самостоятельно воспроизвести условие задачи. Рассмотрим приведенные ниже задачи.

З а д а ч а 9. В саду росло б кустов малины, а смородины — на З куста больше. Сколько кустов смородины росло в саду?

Зад а ча 1 0. Сорока может прожить 27 лет, ласточка в З раза меньше, чем сорока, а ворона — на 40 лет больше, чем ласточка. Сколько лет может прожить ворона?

Задача 11. Водном куске было 32 м ткани, а в другом на 12 м больше. Из всей этой материи сшили платья, расходуя на каждое по 4 м ткани. Сколько платьев сшили?

Эти задачи можно записать кратко.

9а. Малины — 6. кустов;

Смородины — неизвестно, на З куста больше; Сколько смородины?

Учитель должен соблюдать разу4ную меру в использовании символов для краткой записи условия задачи (скобок, стрелок и т. п.). Такая символика это язык, усвоение которого требует от учащихся затрат времени и сил, а возможности его весьма ограничены.

В краткой записи условия отсутствуют многие несущественные элементы, содержащиеся в тексте задачи. Поэтому ученику легче выявить ее математическое содержание. По этой же причине краткая запись выполняет известную обобщающую функцию. Например, краткая запись задачи «У Наташи 8 карандашей, а у Сергея на 5 карандашей больше. Сколько карандашей у Сергея?» во многом будет совпадать с приведенной выше краткой записью задачи 96. Эти задачи относятся к одному типу «Увеличение числа на несколько единиц».

На первых порах краткая запись выполняется учителем при активной «помощи» учащихся. В дальнейшем, усвоив образцы краткой записи, школьники выполняют ее самостоятельно. Краткая запись показывает, хорошо ли ученик понял условие и требование задачи. Работа над краткой записью, как правило, организуется лишь в случаях, когда ученики выбирают неправильный путь поиска решения задачи.

В средних и старших классах навыки краткой записи условия задачи, приобретенные учащимися в начальной школе, используются не только на уроках математики, но и на уроках физики, химии.

Чертеж п о у с л ов и ю з а д а ч и. Следующий уровень интерпретации содержания текстовой задачи чертеж. Он в большей степени, чем краткая запись условия, приближает учащихся к математическому содержанию задачи. В самом еле, отрезки можно складывать, вычитать, умножать и делить на число, поэтому содержание текстовой арифметической задачи можно перевести на наглядный язык отрезков, т. е. выполнить чертеж. Умение «видеть» чертеж, читать его необходимо формировать начиная с первого класса. Учитель должен чаще использовать иллюстративные возможности чертежа.

Предметное воссоздание условия задачи, допускающее получение ответа с помощью пересчета, может использоваться, за редким исключением, только в первом классе. Причем либо при знакомстве учащихся с новым сложным понятием, либо при работе со слабоуспевающими учащимися. В связи с рассмотренными видами интерпретации условия задачи сделаем некоторые замечания.

1. Как известно из психологии, обучение в наибольшей степени выполняет развивающую функцию, если учебный материал преподается учащимся на высоком уровне трудности. Поэтому переход к новому, более наглядному виду интерпретации условия текстовой задачи должен осуществляться только тогда, когда ученики испытывают непреодолимые трудности в поисках решения данной задачи.,, Следовательно, первоначально условие задачи может быть представлено в виде краткой записи, и только потом, по мере необходимости, можно переходить к другим видам наглядности — чертежу, геометрической интерпретации, реальной модели.

2. Реальная модель может быть создана, конечно, не для любой задачи. Как правило, этому препятствуют большие числовые значения или невоспроизводимые в условиях урока явления, рассматриваемые в задаче. В таком случае решается аналогичная задача, лишенная названных недостатков. После того как найдена идея решения, ее применяют к исходной задаче.

Поясним смысл этих замечаний на конкретном примере.

Пусть на уроке учащимся предложена следующая задача: «На одном тракторе работали в течение 60 ч, а на другом — 55 ч. При одинаковом расходе горючего на первом тракторе было израсходовано на 35 л горючего больше, чем на втором. Сколько горючего было израсходовано на каждом тракторе?»

Предположим, что после анализа текста данной задачи учащиеся не в состоянии найти ее решение. В таком случае под руководством учителя они приступают к краткой записи условия. В процессе анализа условия выделяются величины: время работы тракторов, расход горючего в единицу времени (в час), общий расход горючего. Определяется также, какие числовые значения соответствуют этим величинам. Краткое условие может быть записано в следующем виде:

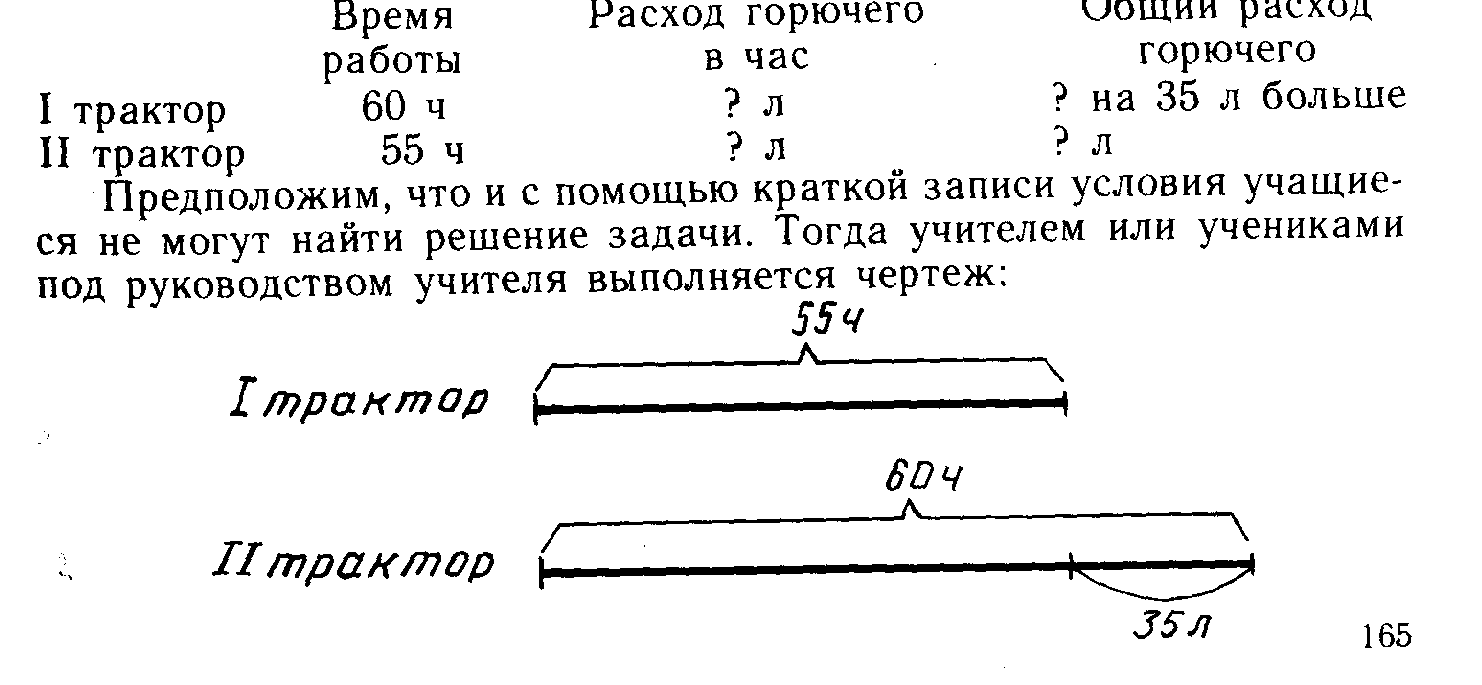
Из чертежа видно, что разности расхода горючего соответствует разность времени работы тракторов. Поэтому уже нетрудно заметить, как определить расход горючего в час.

Если и чертеж не помогает учащимся найти решение задачи, можно перейти к еще более наглядной интерпретации условия с помощью наборного полотна и разрезных фигур. Однако если, например, норму расхода горючего в час обозначить каким-либо символом, то иллюстрация получится чрезвычайно громоздкой. Поэтому вместо исходной задачи рассматривается и иллюстрируется аналогичная ей, но с другими числовыми данными: «На одном тракторе работали в течение 5 ч, на другом З ч. При одинаковом расходе горючего на первом тракторе было израсходовано на 4 л горючего больше, чем на втором. Сколько горючего было израсходовано на каждом тракторе?»:

Иногда при работе над задачей необходимо использовать одновременно два вида интерпретаций. Пусть, например, дана задача:

«Из пунктов А и Б одновременно навстречу друг другу выехали два автомобиля. Один двигался со скоростью 50 км в час а другой

70 км в час. Через 5 ч автомобили встретились. Определить расстояние между А и Б».

для того чтобы учащиеся смогли самостоятельно найти решение 50. 5+70 5, достаточным, возможно, окажется выполнение чертежа. Но для того чтобы ученики увидели более рациональное решение этой задачи (50+70) . 5, нужно объяснить им, что такое скорость сближения и как она выражается математически. Это потребует от учителя использования подвижной модели, т. е. реального воспроизведения характера движения автомобилей.

Навыки выполнения краткой записи условия задач, чертежей по условию задач, приобретенные учащимися в начальной школе, будут полезны им и при решении математических задач в средних и старших классах.

Поиск решения задачи. Решение задач — сложная интеллектуальная Деятельность. Описать ее содержание в полном объеме невозможно, даже если иметь в виду деятельность, осуществляемую младшим школьником.

По существу поиск решения задачи начинается уже при анализе текста задачи и не заканчивается даже тогда, когда ответ получен и проверен. Идея нового способа решения может прийти тогда, когда, казалось бы, получен исчерпывающий ответ на вопрос задачи.

Здесь мы не будем рассматривать внутренние, психические механизмы умственной деятельности ученика, ищущего решение задачи,— это могло бы стать предметом целой книги. Опишем только внешнюю сторону деятельности ученика, который, уже познакомившись с величинами и отношениями, рассматриваемыми в задаче, приступает к поиску математического выражения ее содержания. Остановимся также на общих методических приемах, которыми пользуется учитель, побуждая учащихся к такой деятельности.

В начальной школе обучение учащихся поиску решения задач осуществляется на двух уровнях. Характер деятельности ученика и учителя на каждом пути различен.

Сначала учащиеся учатся находить решение простых задач в одно действие. Умение найти решение такой задачи заключается в том, что ученик может поставить в соответствие отношению, которое связывает числовые данные задачи, арифметическое действие. Например, в задаче: «Скорость автомобиля 80 км в час, а скорость велосипедиста в 4 раза меньше. Определить скорость велосипедиста» две величины — скорость автомобиля и скорость велосипедиста связаны отношением «в... раз больше». Поиск ее решения сводится к выбору действия умножения в соответствии со смыслом данного отношения.

Таким образом, обучение поиску решения простых задач и заключается в формировании у учащихся умения определять, какое арифметическое действие соответствует тому или иному реальному отношению.

Более высокий уровень обучения поиску решения задач осуществляется на множестве составных задач, решаемых в несколько действий.

На первый взгляд может показаться, что для ученика, который умеет решать простые задачи, решение составной задачи не представляет трудности: ведь нужно по существу последовательно решить несколько простых задач. Однако на самом деле все гораздо сложнее.

Рассмотрим задачу: «Пионеры собрали 80 кг макулатуры, а октябрята — на 20 кг меньше. Сколько макулатуры собрали оба отряда вместе?» В условии простой задачи известны, как правило, два числовых значения каких-либо величин и некоторое отношение, которое их связывает. В данной задаче также известны два числовых значения и два отношения — «на... меньше» и «оба... вместе». Ученик, умеющий решать простые задачи, знает, что если «на... меньше», то нужно выполнить вычитание, а если оба... вместе»,— сложение. Но для решения приведенной задачи этих знаний недостаточно. Нужно еще определить, разность значений каких величин необходимо вычислить; сумму значений каких величин необходимо найти. Таким образом, поиск решения составных задач качественно отличается от поиска решения простых задач. Качественно другой должна быть и методика обучения поиску решения составных задач. Классифицировать составные задачи по типам соответствующих им числовых выражений нецелесообразно*. Поэтому система составных задач, решаемых в начальной школе, очерчена весьма условно: это задачи, требующие выполнения не более трех действий, в их числе задачи на пропорциональность и на движение. Это обстоятельство и обусловливает основную особенность методики обучения учащихся поиску решения составных задач. Эта методика должна быть ориентирована на формирование у учащихся общих методов поиска решения, соответствующих интеллектуальным возможностям младших школьников. К таким методам относятся аналитический, синтетический и аналитико-синтетический. Аналитический метод. Анализ логический прием, состоящий в расчленении исследуемого объекта на составные элементы в исследовании каждого из них в отдельности. Он может использоваться многократно. В задаче исследуемый объект описывается в требовании. Однократно или многократно расчленяя объект, приходят, наконец, к составляющим, которые даны в условии задачи (если, конечно, данная задача имеет решение). Аналитический метод состоит в многократном последовательном использовании анализа. Применительно к текстовым задачам аналитический метод позволяет расчленить составную задачу на систему простых задач. Поясним это на примере. За да ч а 12. За 4 м сукна заплатили столько же, сколько за 14 м шелка. Цена шелка б р. за метр. Какова цена сукна? Расчленим объект, описываемый в требовании. Для этого воспользуемся следующим соображением: чтобы определить цену сукна, достаточно взять количество купленного сукна и его стоимость. Другими словами, достаточно решить простую задачу, в условии которой сказано, сколько купили сукна и сколько за него заплатили. В исходной задаче первая величина известна, а вторая — нет. Поэтому повторно используем прием анализа: выясним, какие компоненты определяют стоимость сукна. * Пусть, например, составные задачи классифицированы по следующему принципу: задачи относятся к одному типу, если их содержание описывается числовыми выражениями, имеющими одинаковый вид (а + Ь + с, или а + Ь — с, или а:Ь + с — й и т. д.). Так, задачи: В колхозной бригаде 5 гусеничных тракторов, а колесных на З больше. Сколько всего тракторов в бригаде и <В школе работают З спортивные секции: легкоатлетическая, гимнастическая и футбольная. В легкоатлетической занимается 15 школьников, в гимнастической — 27, а в футбольной — на 9 человек больше, чем в легкоатлетической и гимнастической вместе. Сколько человек занимается в футбольной секции? относятся к одному типу, так как их общий вид: а + Ь + с. Определим, какое количество типов задач, решаемых в два действия, возможно щи такой классификации. Воспользуемся формулой для размещений с повторениями А4= 42, де 4— количество арифметических операций; 2 — количество операций, необходимых для решения каждой задачи. Задачи в три действия подразделяются на 64 типа (А = 4 ). Таким образом, классификация составных задач содержала бы 80 (!) типов задач и, конечно, были бы неприменима на практике. -

В исходной задаче сказано, что за сукно заплатили столько же, Сколько за шелк. Значит, нужно решить простую задачу, в условии которой даны количество купленного шелка и его цена. Значения и той и другой величины известны из условия исходной задачи. Итак, составная задача с помощью аналитического метода расчленена на две простые задачи, причем ответ к одной из них является данным условия другой: «Купили 14 м шелка по цене б р. за метр. Сколько стоит купленный шелк? и «Купили 4 м сукна и заплатили? рублей (столько же, сколько за шелк). Какова цена сукна? Поиск решения задачи, осуществляемый младшим школьником, можно рассматривать как следующий процесс: ученик задает себе вопросы и отвечает на них. В таком случае обучение поиску решения задачи состоит главным образом в обучении учащихся задавать эффективные вопросы по содержанию задач и правильно на них отвечать. Аналитический метод можно также представить в виде системы вопросов и ответов. Для рассмотренной выше задачи эта система имеет следующий вид. 1. Что нужно знать, чтобы определить цену сукна? Ответ: Количество купленного сукна и его стоимость. Iа. Известно ли, сколько купили сукна? Ответ: Да. 16. Известно ли, сколько заплатили за сукно? Ответ: Нет. Последний вопрос и отрицательный ответ на него дают основание задать следующий вопрос. 2. Что нужно знать, чтобы определить стоимость сукна? Ответ: Стоимость шелка. 2а. Известна ли стоимость шелка? Ответ: Нет. Так как на вопрос 2а получен отрицательный ответ, то формулируется еще один вопрос. З. Что нужно знать, чтобы определить стоимость шелка? Ответ: Количество купленного шелка и его цену. За. Известно ли, сколько куплено шелка? Ответ: Да. 36. Известна ли цена шелка? Ответ: Да. Итак, идея решения задачи найдена. Отметим, что количество вопросов и их содержание обусловливаются содержанием и способом решения задачи. И основные и вспомогательные вопросы имеют вполне определенную конструкцию. Формулировать их и давать на них ответы школьники учатся в процессе решения простых задач (в данном случае — простых задач на нахождение стоимости по цене и количеству купленного, на нахождение цены по стоимости и количеству). Синтетический метод. Синтез — логическая операция установления связи между составными частями исследуемого объекта и изучения его как единого целого. Исследуемый объект называется в требовании задачи, а его элементы описываются в условии. Сущность синтетического метода поиска решения задачи состоит в установлении связей между данными условия задачи и получении таким образом новых данных. Затем устанавливаются связи между полученными данными и так далее, до тех пор, пока не будет получено требуемое. Поясним это на примере задачи, которая была рассмотрена выше. Условие этой задачи включает следующие данные: «куплено 4 м сукна», «куплено 14 м шелка», «за купленное сукно заплатили столько же, сколько за шелк», «цена шелка б р. за метр». Представим синтетический метод как систему вопросов и соответствующих ответов. Тогда связь между данными условия устанавливается следующим образом. 1. Что можно определить, зная, что купили 14 м шелка и цена шелка б р. за метр? Ответ: Стоимость купленного шелка (6. 14=84). 2. Что можно определить, зная, что было куплено 4 м сукна и 14 м шелка? Ответ: Количество купленной материи (4+14=28); на сколько больше (меньше) было куплено шелка (сукна), чем сукна (шелка) (14—4= 10). Очевидно, что установить какие-либо другие связи между данными условия нельзя. В то же время ни одно из полученных данных не является требуемым. Поэтому синтез продолжается: раскрываются связи между новыми данными и приведенными в условии. 3.Что можно определить, зная, что за шелк заплатили 84 р. (и что за сукно заплатили столько же)? Ответ: Стоимость купленного сукна (84 р.). 4. Что можно определить, зная, что за 4 м сукна заплатили 84 р.? Ответ: Цену сукна (84:4=21). Итак, ответ получен. Заметим, что не все промежуточные результаты необходимы для решения — задача решается только в два действия. Однако, возможно, «лишние» данные пригодились бы, если бы эта задача имела другое требование. Аналитико-синтетический метод. Рассмотрим метод, который значительно чаще, чем аналитический и синтетический, используется на практике. Он сочетает элементы и анализа и синтеза. Проиллюстрируем его на примере. З а д а ч а 13. Школа закупила для уроков труда нитки, ткань и ножницы. За нитки уплатили 2 р., за ткань -—- 15, а за ножницы — на З р. больше, чем за нитки и ткань вместе. Сколько стоила вся покупка? Система вопросов и ответов, отражающая процесс поиска решения задачи, может иметь следующий вид. Анализ. 1. Что нужно знать, чтобы определить стоимость покупки? Ответ: Стоимость ниток, ткани и ножниц. Iа. Известна ли стоимость ниток? Ответ: да, 2 р. 16. Известна ли стоимость ткани?

‘Ответ: да, 15 р. Iв. Известна ли стоимость ножниц? Ответ: Нет. Синтез. 2. Что можно узнать из условия задачи? Ответ: Сколько стоили нитки и ткань вместе (2+15= 17). Синтез. 3. Что можно узнать, зная стоимость ниток и ткани? Ответ: Стоимость ножниц (17+З20). Итак, идея решения задачи найдена: сначала нужно найти, сколько стоят нитки и ткань вместе, затем сколько стоят ножницы и, наконец, СКОЛЬКО стоит вся покупка. Обучение учащихся начальных классов рассмотренным методам Поиска решения задач Сводится к обучению их правильному (как минимум по форме) формулированию вопросов, соответствующих аналитическому или синтетическому методу. В старших классах обучение учащихся этим методам будет продолжено (см., например Ю. М. Колягин и др. Методика преподавания математики в средней школе.— М: Просвещение, 1975). Основным средством обучения младших школьников приемам Поиска решения задач являются образцы рассуждений (вопросов- ответов), которые демонстрирует учитель. Вместе с тем такая работа может вестись и целенаправленно. Уже в 1 классе учитель обращает внимание учащихся на то, что в процессе решения задачи могут формулироваться разные по форме вопросы, что форма вопроса определяет особенности ответа на него. Пусть, например, первоклассникам предложена задача: «В вазе лежат 2 яблока и З груши. Сколько фруктов в вазе?» Учитель формулирует вопрос, соответствующий аналитическому методу: «Что нужно знать, чтобы определить, СКОЛЬКО фруктов в вазе?» Учащиеся отвечают (возможно, с помощью учителя): «Нужно знать, СКОЛЬКО В вазе яблок и сколько груш». Затем учитель формулирует вопрос, соответствующий синтетическому методу: «Что можно определить зная, что в вазе было 2 яблока и З груши?» Самостоятельно ИЛИ с помощью учителя ученики приходят к следующему ответу: «Можно узнать, СКОЛЬКО всего фруктов в вазе, или на сколько больше в вазе груш, чем яблок, или на сколько в вазе меньше яблок, чем груш». Затем анализируются особенности первого и второго вопросов и особенности ответов на каждый из них. Выясняется, например, что первый вопрос задается исходя из того, что спрашивается в задаче; в задаче спрашивается: «Сколько фруктов в вазе?». Значит, начиная решать задачу, мы спрашиваем: Что нужно знать, чтобы определить сколько фруктов в вазе? Чтобы ответить на этот вопрос, можно даже не знать условия задачи, причем ответ возможен только один — нужно знать, сколько в вазе фруктов каждого вида. Второй вопрос задается исходя из того, что дано в условии задачи: известно, что в вазе 2 яблока и З группы, значит, начиная решать задачу, мы спрашиваем: Что можно оп ред ел и т ь, з н а я, что в вазе 2 яблока и З груши? Чтобы ответить на этот вопрос, можно и не знать, что спрашивается в задаче, причем ответов может быть несколько. Понятно, что такая работа начнет приносить плоды только при систематическом и целенаправленном ее проведении. Конечно, она потребует определенных, возможно, существенных, затрат времени, но ее полезность это оправдывает. Существуют и другие возможности обучения методам поиска решения задач младших школьников. Они описываются в книге В. Л. Дрозда и др. «Практикум по методике начального обучения математике» (Мн., Выш. шк., 1984). ‚ Проверка решению задачи. Наиболее оперативным способом про- 4) верки решения задачи является 2л чевного учениками ответа с ответом, который сообщается учителем. Иногда, еще до того как ученики приступили к решению задачи, учитель называет несколько ответов, из которых только один правильный. Это Оправдывается в тех случаях, когда можно предугадать, какую ошибку могут допустить учащиеся при решении данной задачи. Задача 14. Отряд октябрят собрал 5 кг лекарственных трав, а отряд пионеров — в 4 раза больше. Сколько лекарственных трав собрали пионеры? Если опыт решения задач такого типа (на увеличение числа в несколько раз) у учащихся невелик, то легко предугадать возможную ошибку в решении: 5+4. В самом деле, школьникам хорошо известно, как решаются задачи на увеличение числа на несколько единиц («Отряд октябрят собрал 5 кг лекарственных трав а отряд пионеров — на 4 кг больше. Сколько лекарственных трав, собрали пионеры?»). Поэтому на доске перед началом самостоятельной работы учащихся над задачей могут быть записаны два ответа: 9 кг и 30 кг, Задача 15. С одного поля собрали9отб зерна, а с другого 2/3 этого количества. Сколько зерна собрали со второго поля? Учитель заранее может предположить, например, что: 1) учащиеся неправильно выполнят перевод единиц массы: 90 т б ц —96 ц, тогда 96:3=32, 32. 2=64; ответ: 64 ц, или б т 4 ц; 2) учащиеся будут неправильно находить дробь числа: 906:2= 453, 453. 3=1359; ответ: 1359 ц, или 135 т 9 ц. В таком случае одновременно с условием задачи учитель сообщает возможные ответы: 64 ц; 60 т 4 ц; 1 359 ц; б т 4 ц; 135 т 9 ц. В начальной школе могут использоваться и другие виды проверки ‚(широко применямые учащимися в средних и стар их классах): прикидка ответа, решение задачи1 другим способом, сопоставление / ответа и данных условия задачиф5ешение задачи, обратной данной. Отметим, что в начальных классах учитель должен не только показать учащимся возможные способы проверки решения задачи, но и потребовать от них выполнения проверки (особенно в тех случаях, когда задача решается самостоятельно). Прикидка ответ а — достаточно простой способ проверки решения задачи. Суть его состоит в том, что исходя из условия задачи, не выполняя, как правило, каких-либо вычислений, определяют границы, в которых должен находиться ответ.

З ад а ч а 16. В букете было несколько роз. Четыре розы подари- В букете осталось восемь роз. Сколько роз было в букете? вполне вероятно, что некоторые учащиеся могут прийти к неправильному решению (8—4=4) исходя из того, что часть роз отдали и количество уменьшилось. Вместе с тем легко показать, что в ответе должно получиться число, большее, чем 4 и 8. Такая прикидка ответа убеждает что данная задача решается сложением. Задача 17. Для уоков рисования купили 5 наборов карандашей и 7 наборов красок по такой же цене. За всю покупку уплатили 8 р. 40 к. Сколько стоили карандаши и сколько стоили краски? Еще до решения задачи можно обсудить, в каких границах будут лежать искомые числовые значения. Во-первых, и стоимость карандашей, и стоимость красок меньше 8 р. 40 к. Во-вторых, карандаши сто дешевле, чем краски. -- Вместе с тем данный способ проверки не очень надежен в самом деле, если в результате ошибок в вычислениях ученик получит ответы З р. 20 к. и 4 р. 50П, то проверка прикидкой эти ошибки не вскрыла бы. Решение задачи другим способом обеспечивает более эффективную проверку. За дача 18. Из двух городов навстречу друг другу одновременно выехали два автомобиля. Один ехал со скоростью 60 км в час, а другой —70 км в час. Через З ч автомобили встретились. Определить расстояние между городами. Задача может быть решена двумя способами: 60 3+70. 3 и (60+70). 3. Получение учащимися одинаковых ответов и в первом и во втором случаях свидетельствует о том, что они верны. Однако этот способ проверки можно использовать не всегда, так как не для ВСЯКОЙ задачи существуют разные варианты решения. Кроме того, если даже задачу можно решить несколькими способами, то затраты времени на их поиск могут оказаться неоправданными. В некоторых случаях для проверки решения с оп ост а в л я ют с я ответ и данные условия задачи. Обратимся к задаче 17. Предположим, что ученик получил неверный ответ: карандаши стоят З р. 20 к., а краски — 4 р. 50 к. Этот ответ Можно сопоставить с данными задачи «за всю покупку уплатили 8 р. 40 к.». В самом деле, 320+450 должно равняться 840, однако З20+450840, значит, задач решена неверно. 1 За дача 19. В двух школах 1850 учен1ов. В одной из них на 48 учеников меньше. Сколько учащихся4каждой школе? Решая эту задачу, ученики могут использовать неверную идею: 1 850:2= 925 — СТОЛЬКО учащихся в одной школе; 925+48= 973 — во второй. В результате сопоставления полученных ответов с данными условия «в двух школах 1 850 учеников» получается, что 925+973 1 898. Значит, полученное решение неверно. Но и этот способ можно использовать далеко не всегда. Например, он непригоден для проверки решения задачи 12. Наиболее эффективным, хотя и весьма трудоемким, является способ проверки решения, который состоит в р е ш е н и и з а д а

/обратной данной. /

Пусть, например, этим способом нужно проверить решение задачи

12. Для этого составляется обратная задача: полученный ответ — расстояние между городами 390 км — включается в условие задачи;

какое-либо данное условие задачи выбирается искомым, например скорость первого автомобиля; формулируется обратная задача: «Из двух городов, расстояние между которыми 390 км, навстречу друг другу одновременно выехали два автомобиля. Один из них ехал со скоростью 70 км в час. Через З ч автомобили встретились. С какой скоростью ехал другой автомобиль?» Если при решении этой задачи будет получен ответ 60 км в час, то это означает, что задача 12 решена верно.

Недостатком данного метода проверки является не только его трудоемкость. Решая задачу, обратную данной (которая, кстати говоря, иногда оказывается сложнее исходной), ученик может допустить ошибку и на основании этого предположить, что исходная задача решена неверно. А это может не соответствовать действительности.

20. ОБУЧЕНИЕ УЧАЩИХСЯ РЕШЕНИЮ ПРОСТЫХ ЗАДАЧ

Классификация простых задач. Выше был определен возможный принцип классификации простых задач: важнейшим математическим понятиям программ по математике соответствуют специальные типы простых задач.

Центральное место в программе по математике для начальных классов занимает понятие целого неотрицательного числа. Из вузовского курса математики известно, что каждое понятие характеризуется объемом и содержанием. Объем понятия целого неотрицательного числа раскрывается в начальной школе в процессе обучения учащихся счету, нумерации.

Содержание понятия целого неотрицательного числа представляется учащимся как совокупность следующих свойств: на множестве целых неотрицательных чисел выполнимы операции сложения и умножения (частично выполнимы вычитание и деление), множество целых неотрицательных чисел строго упорядочено. Это содержание раскрывается главным образом с помощью текстовых арифметических задач. Исходя из этой, так сказать, математической, точки зрения, простые задачи, решаемые в начальной школе, должны подразделяться на два класса: задачи, посредством которых у учащихся формируется представление об арифметических операциях, и задачи, которые раскрывают учащимся смысл отношений «больше», «меньше», «равно».

Однако с методической точки зрения такая классификация малоэффективна. Известно, что математические понятия усваиваются лучше, если они изучаются во взаимосвязи, сопоставляются и противопоставляются. Операции сложения и вычитания, так же как и операции умножения и деления, взаимообратны, поэтому и изучать их целесообразно во взаимосвязи. таким образом, наряду с двумя навИНЫМИ классами задач необходимо выделить задачи, раскрывающие связь между взаимнообратными арифметическими действиями И.

задачи, раскрывающие учащимся смысл отношений порядка, также должны удовлетворять определенным методическим условиям. В самом деле, в житейских ситуациях эти отношения представляются , как правило, в виде отношений «больше на (в)» и ‚<меньше на (в)$ Например, когда на практике сравниваются численности элементов двух множеств, недостаточно установитъ численность какого множества больше или меньше. Нужна более подробная характеристика: на сколько элементов больше (меньше) или во сколько раз больше (меньше). Приходится решать и обратные задачи, когда известна численность элементов одного множества, а о другом известно только, что численность его элементов на несколько единиц больше (меньше) или в несколько раз больше (Меньше).

Итак, получаем следующую систему задач, через которую раскрывается содержание понятия целого неотрицательно числа:

Ясно, что данной классификацией не исчерпываются все типы простых задач, решаемых в начальной школе. Существует еще множество понятий (в частности, нематематических, таких, как скорость, цена, урожайность и т. д.), смысл которых также раскрывается через простые задачи Однако обучение решению соответствующих задач возможно только на основе знаний о целых неотрицательных числах, поэтому методику обучения их решению мы рассмотрим в конце данного параграфа.

Простые задачи, решаемые сложением и вычитанием. Рассмотрим конкретное содержание определенной выше системы применительно к арифметическим операциям первой ступени — сложению и вычитанию. Выделим следующие типы задач:

1) задачи, раскрывающие смысл операции сложения;

2) задачи, раскрывающие смысл операции вычитания;

3) задачи, раскрывающие связь между операциями сложения и вычитания;

4) задачи, раскрывающие смысл отношений «увеличить на (несколько единиц)» и «уменьшить на (несколько единиц));

5) задачи, раскрывающие СМЫСЛ отношений «больше на» и «меньше на» (задачи на сравнение чисел с помощью вычитания, т. е. на разностное сравнение).

Аналогичным образом выделяются типы простых задач, решаемых умножением и делением:

1) задачи, раскрывающие смысл операции умножения;

2) задачи, раскрывающие смысл операции деления;

3) задачи, раскрывающие связь между умножением и делением;

4) задачи, раскрывающие смысл отношений «увеличить в несколько раз» и «уменьшить в несколько раз»;

5) задачи, раскрывающие смысл отношений «больше в ... раз» и «меньше в ... раз» (задачи на кратное сравнение).

Последовательность введения задач указанных типов может быть различной. Например, задачи на разностное сравнение (на кратное сравнение) могут быть рассмотрены раньше, чем задачи на увеличение (уменьшение) числа на несколько единиц (на увеличение (уменьшение) числа в несколько раз).

Выделенные 10 типов задач являются основными, однако ими, как уже отмечалось, не исчерпывается все многообразие простых задач, решаемых в начальных классах. И это естественно, так как с помощью задач у учащихся формируются представления не только об арифметических операциях, отношениях «больше), «меньше), «равно», но и о некоторых других математических понятиях, например о дроби. Методические особенности обучения детей решению этих задач будут рассмотрены в конце данного параграфа.

Остановимся на основных вопросах методики обучения учащихся решению задач каждого из выделенных типов.

Задачи, раскрывающие смысл операции сложения. Это первые задачи, с которыми встречаются учащиеся. Здесь они знакомятся с понятиями: «условие задачи» («о чем говорится в задаче?»), «вопрос» или «требование задачи» («что необходимо найти?», «о чем спрашивается в задаче?»); получают представление о краткой записи условия задачи, учатся выполнять предметные иллюстрации по ее содержанию, т. е. приобретают опыт использования общих приемов работы над текстовой задачей.

В качестве исходных могут служить, например, следующие задачи: «Сережа нашел 2 белых гриба и З подосиновика. Сколько грибов нашел Сережа?; «У Наташи 2 куклы, а у Сережи заводных автомобиля. Сколько игрушек у Наташи и Сережи вместе?»; «На дереве сидели 2 синицы. Прилетели З снегиря. Сколько птиц стало на дереве?»

\Сравнивая выполненные учителем краткие записи условий задач учащиеся могут убедиться, что, несмотря на разные сюжеты, эти задачи имеют и общее: в условии — два числовых данных и требуется найти «сколько всего» (грибов, игрушек, птиц). для того

чтобы ученики осознанно выбрали арифметическое действие для решения задач данного типа, учитель должен рассмотреть с ними со

ответствующие предметные иллюстрации.

Из вузовского курса математики известно, что существуют два

подхода к определению операции сложения — теоретико-множественный и аксиоматический. В начальной школе используется первый

подход: суммой чисел а и Ь называется такое число с, которое выражает численность элементов множества С=А [‚В (А ПВ— ), где

численность элементов множеств А и В выражается соответственно числами а и Ь. Этим и определяется характер иллюстраций, раскрывающих математическое содержание задач рассматриваемого

типа.

Рассмотрим один из вариантов знакомства учащихся с операцией

сложения на примере задачи: «Сережа нашел 2 белых гриба и З под

осиновика. Сколько грибов нашел Сережа?»

После анализа текста задачи ее содержание иллюстрируется на

наборном полотне (рис. 51).

«Чтобы ответить на вопрос задачи: Сколько всего грибов нашел

Сережа,— говорит учитель,— положим и белые грибы и подосиновики в одну корзинку (устанавливает

«грибы» в одном кармашке наборного полотна). Сколько грибов мы

положили в корзинку? 2 белых и З подосиновика. в математике

говорят так: к двум прибавили

три. На математическом языке это

записывается: 2 + З. Сколько грибов оказалось в корзинке? Пять. В математике говорят: «К двум

прибавить три равняется пяти» и записывают: «2 + З = 5.

Таким же образом решается несколько подобных задач. При этом

учитель должен показать учащимся, что практические действия

определенного рода над двумя множествами предметов описываются

в математике одинаково — как сложение двух чисел.

Необходимость в предметных иллюстрациях может довольно бы

стро исчезнуть. Во-первых, потому, что они достаточно трудоемки и

громоздки. Во-вторых, сюжеты задач данного типа схожи в том

смысле, что имеют вид: «Есть а и Ь. Сколько всего?»- или «Есть а.

Приехало (прилетело, приплыло, купили, нашли и т. д.) Ь. Сколько

стало?» Поэтому учащиеся и без помощи иллюстраций определяют,

каким действием решается задача.

Очень важным компонентом методики работы над задачами является использование учителем упражнений такого рода: «В саду растут яблони и груши. Составьте такую задачу, чтобы она решалась так: 4+2 «Составьте задачу о снегирях и синицах, чтобы она решалась так: 3+2»; «Составьте задачу, чтобы она решалась так:

5+3»ит.д. /

Задачи, раскрывающие смысл операции вычитания. Известно, что изучение понятий во взаимосвязи противопоставлении, выявлении общего) способствует более качественному усвоению учащимися каждого из этих понятий. Поэтому обучать школьников решению задач, раскрывающих смысл сложения и вычитания, необходимо одновременно. Так как сложение определяется через объединение непересекающихся множеств, то вычитание также определяется через операцию на множествах. Разностью чисел а и Ь называют такое число с, которое выражает численность элементов множества С= = А\В (В А), где численность элементов множеств А и В выражается соответственно числами а и Ь.

Рассмотрим возможный вариант знакомства учащихся с операцией вычитания с помощью задач соответствующего типа. Школьникам, например, предлагается такая задача: «У Наташи б флажков. два она отдала брату. Сколько флажков осталось у Наташи?». После анализа текста задачи ученики под руководством учителя выполняют иллюстрацию ее содержания на наборном полотне. В наборное полотно устанавливается б флажков. Затем выполняется действие 2 флажка удаляются (рис. 52). Констатируется: было

б флажков, 2 убрали, осталось 4. «В математике,— говорит учитель,— выполненное решение задачи записывается так: 6—2=4. Говорят, что от б отняли 2, или из б вычли 2 и получили 4».

Аналогично можно решить еще несколько задач. В дальнейшем учащиеся определяют необходимое для решения арифметическое действие без иллюстраций, используя опорные слова условия: «Было а. Уехало (улетело, уплыло, израсходовали и т. д.) Ь. Сколько осталось?»

Наряду с решением задач ученики должны выполнять задания по составлению задач по данному выражению.

Задачи, раскрывающие связь между сложением и вычитанием. При решении задач первых двух типов у учащихся может сложиться представление, что для решения задачи достаточно найти в условии или требовании опорное_ слово и по нему определить арифметическое действие. Поэтому необходимо перейти к задачам, в которых хорошо «работавшие» ранее опорные слова не только не помогав т правильно выбрать арифметическое действие, но и могут ввести в заблуждение. Приведем примеры таких задач.

задача 20. Сережа подарил Юре 2 марки, а Коле -— З марки.

Сколько марок подарил Сережа?

Зад а ч а 2 i. у Сережи было несколько марок. Три марки ему подарили. У него стало 8 марок. Сколько марок было у Сережи в начале?

Задача 22. у Сережи было З марки. Ему подарили несколько марок. Всего у него стало 8 марок. Сколько марок подарили Сереже?

Задача 23. у Сережи было несколько марок. Три марки он

подарил другу. После этого у него осталось 5 марок. Сколько марок

было у Сережи вначале?

Слово «подарил» (т. е. отдал) в задаче 20 «подсказывает», что она решается вычитанием, слова «Сереже подарили» (т. е. дали) в задаче 21 обусловливают действие сложения. На самом же деле эти

задачи решаются соответственно обратными действиями.

Особенность задач 21—23 состоит еще и в том, что математически их содержание может быть выражено двояко: и уравнениями (х+ +а = Ь, а + х = Ь, х — а Ь) и выражениями (Ь а, а + Ь). С помощью таких задач у учащихся могут формироваться начальные представления об уравнениях, о связи между сложением и вычитанием. В целом же задачи 20—23 представляют собой сложные варианты задач на нахождение суммы и разности, они требуют от учащихся глубокого понимания сущности операций сложения и вычитания, осуществления довольно сложной умственной деятельности. для того чтобы деятельность такого рода была возможна, на начальном этапе обучения решению таких задач необходимо использовать предметные

иллюстрации. Причем работу с иллюстрациями учащиеся смогут выполнять с большей самостоятельностью, чем раньше,— ведь у них уже есть некоторый опыт. Рассмотрим ее содержание на примерах задач 20 и 21.

В соответствии с условием задачи 20 заполняются два кармашка наборного полотна. В один устанавливаются 2 кружка (т. е. «марки»), а в другой — З кружка. Чтобы определить, сколько всего марок подарил Сережа, кружки укладываются в один кармашек, т. е. выполняется объединение двух множеств. Выполненное руками действие учащиеся уже умеют называть и записывать на математическом языке -— «к двум прибавили три», 2+3.

В условии задачи 21 содержатся два числовых данных и фигурирует слово подарили, т. е. “дали возможно, учащимся покажется, что в наборном полотне в разных кармашках нужно поместить два множества З кружка («марки») и 8 кружков. Однако легко показать, что в задаче рассматривается восьмиэлементное Множество и его подмножество, содержащее З элемента, В самом деле, 8 марок у

Сережи стало после того, как ему подарили З марки. Таким образом, иллюстрация

вид: в кармашек наборного полотна устанавливается 8 <марок и З из них Выделяются, например, цветом. Чтобы определить, сколько марок было у Сережи первоначально, нужно из кармашка удалить З «марки». Эта операция, как уже известно учащимся, на математическом языке называется: <от 8 отняли З» или «из Восьми вычли три» и описывается 8—З.

Аналогичным образом математизируется содержание задач 22 и 23.

Решая задачи, подобные задачам 20—23, учащиеся могут иллюстрировать их содержание самостоятельно с помощью индивидуального разрезного материала.

Накопив опыт решения задач, ученики смогут обходиться и без наглядности. Пусть, например, предложена задача: «На уборке урожая работало 4 колесных и несколько гусеничных тракторов. Всего на уборке было занято 7 тракторов. Сколько из них было гусеничных?» Решая ее, школьники могут рассуждать примерно так: «Всего работало 7 тракторов, из них 4 колесных. Значит, гусеничных было меньше семи, поэтому от 7 нужно отнять 4». Вместе с тем предметные иллюстрации не теряют полностью своего значения даже тогда, когда учащиеся накопили значительный опыт решения задач данного типа. Иногда ученик, подчас совершенно неожиданно для учителя, не может решить задачу хорошо изученного типа. Конечно, учитель может предложить «сильному» ученику рассказать, как эта задача решается. Однако гораздо полезнее побудить ученика, не решившего задачу, проиллюстрировать ее содержание. Работа с иллюстрацией, очевидно, самый естественный и надежный путь к осознанию учащимися, почему данная задача решается сложением или вычитанием. Кроме того, по работе ученика с наглядностью учитель может проследить за его рассуждениями, которые он далеко не всегда может выразить словами. Таким образом, иллюстрации, выполняемые учащимися, играют роль обратной связи (ученик — учитель).

Задачи на увеличение (уменьшение) числа на несколько единиц. Обучение учащихся решению задач данного типа может показаться на первый взгляд очень простым делом. Пусть, например, ученикам предлагается задача нового типа: «У Сережи З карандаша, а у Наташи на 2 карандаша больше. Сколько карандашей у Наташи?» Практика показывает, что многие школьники без всякой помощи со стороны учителя в состоянии получить правильное решение: 3+2. И это не удивительно. На протяжении длительного времени учащиеся решали задачи, раскрывающие смысл операции сложения. Поиск решения сводился к следующему: в условии задачи выделялись два числовых данных и опорное слово, которое обусловливало выбор арифметического действия. Данная задача как будто дает учащимся возможность использовать этот опыт — в условии даны два числа, есть опорное слово больше», которое «подсказывает», что нужно выполнить действие сложения. Однако такой механический перенос умений на новый тип задач не должен, конечно, удовлетворять учителя. Правильное решение еще не свидетельствует о том, что ученик понимает, почему данная задача решается именно так, а не иначе.

Например, нескольким ученикам, правильно решающим рассмотренную выше задачу, было предложено проиллюстрировать ее решение на наборном полотне с помощью кружков. Красными кружками обозначались карандаши Сережи, а синими

карандаши Наташи. Учащиеся установили в кармашек З красных кружка, а затем 2 синих. Полученное множество кружков отождествлялось с множеством карандашей Наташи. У школьников спрашивали: если 5 кружков — это карандаши Наташи, то почему среди них есть красные кружки — карандаши Сережи? Этот вопрос ставил школьников в тупик Подробно рассмотрим идею решения задачи о карандашах. Пусть множество А состоит из Сережиных карандашей, а множество В содержит только два Наташиных карандаша. Понятно, что объединение этих множеств не является Наташиными карандашами. На предматематическом уровне решение задачи состоит в объединении множества В с некоторым множеством С, содержащим остальные карандаши Наташи (рис. 53). Численность С в условии задачи не указана. Ее можно найти, используя предматематическое определение отношения «больше» («меньше»), с которым учащиеся знакомились в дочисловой период: множество М содержит больше элементов, чем множество А (Или А содержит меньше элементов, чем М), если при укладывании элементов из М и А парами окажется, что у каждого элемента из А есть пара, а у некоторых элементов из

больше, чем у Сережи. Значит,

карандаши из А и С можно уложить парами, а у карандашей из

множества В пары нет. Поэтому А -- С, т. е. С содержит З элемента. Чтобы ответить на вопрос задачи, нужно посчитать, сколько карандашей в множестве С [.. В, или, если говорить на языке арифметики, найти сумму

З + 2

Итак, хотя арифметически задачи на увеличение числа на несколько единиц решаются так же, как и задачи, раскрывающие смысл операции сложения, на предматематическом уровне их решения существенно различаются. Задачи на увеличение числа решаются фактически в два действия: 1) определяется численность множества, о котором непосредственно в условии задачи не говорится; 2) выполняется операция объединения двух множеств.

Совершенно аналогично можно раскрыть предматематический смысл решения задач на уменьшение числа на несколько единиц. Пусть, например, нужно решить задачу: «У Сережи 5 карандашей, а у Наташи на З карандаша меньше. Сколько карандашей у Наташи?» В условии задана численность двух множеств. Множество А содержит 5 элементов — это карандаши Сережи, множество В содержит З элемента. Понятно, что множество В — это и не Сережины и не Наташины карандаши Чтобы определить его смысл, нужно снова воспользоваться определением отношения «меньше» (рис. 54). Оказывается, что в задаче подразумевается еще одно множество — С. Из рис. 54 видно, что это карандаши Наташи в случае, если бы у нее их было столько же, сколько у Сережи. Таким образом, численность С равна 5. А В — это подмножество С, которое нужно удалить в соответствии с условием задачи Мчот и Наташи

НЫХ карандашей. На языке арифметики решение данной задачи описывается выражением 5—3.

Осознание учителем рассмотренных особенностей задач на увеличение (уменьшение) числа на несколько единиц позволяет ему выработать эффективную стратегию обучения учащихся их решению.

Основой обучения решению задач данного типа является определение понятия больше» («меньше>, «равно»), которое формировалось у учащихся на первых уроках математики. Поэтому полезны будут задания практического характера, позволяющие организовать работу учащихся с индивидуальными средствами наглядности.

1. Возьмите 7 красных и 5 синих кружков. Разложите их на парте парами так, чтобы под кружком одного цвета лежал кружок другого цвета.

Результаты работы обсуждаются. Кружки какого цвета остались без пары? Красные. Вспомним, что это означает. Что красных кружков больше, чем синих. Мы доказали, что 7 больше 5.

Какого цвета кружков не хватает, чтобы все кружки лежали парами? Синих. Вспомним, что это означает? Синих кружков меньше, чем красных. Мы доказали, что 5 меньше 7.

Сколько красных кружков осталось без пары? Это означает, что красных кружков на 2 больше, чем синих, или 7 на 2 больше, чем 5.

Сколько нужно добавить синих кружков, чтобы все кружки лежали парами? Два. Это означает, что синих кружков на 2 меньше, чем красных, или 5 на 2 меньше, чем 7.

2. Положите на парте б красных кружков. Под каждым из них положите по синему кружку. Сколько синих кружков?

Положите еще столько синих кружков, чтобы их было на 2 (на З, на 1) больше, чем красных.

Сколько теперь красных кружков нужно положить, чтобы их стало столько же, сколько синих?

Уберите столько синих кружков, чтобы их стало на 2 (на З, на 1) меньше, чем красных. И так далее.

Результаты работы над этими заданиями ученики могут записывать в тетрадях с помощью числовых выражений.

З. Цоложите на парте 5 красных кружков. Положите столько же синих кружков; положите на 2 синих кружка больше (меньше), чем красных, и т. д.

Выполнение заданий сопровождается соответствующими записями в После такой подготовительной работы (она может быть выполнена в большем или меньшем объеме) можно приступать к обучению решению задач нового типа.

Пусть в качестве исходной будет рассмотрена задача: «Возле школы пионеры посадили З клена, а лип на 2 больше. Сколько лип посадили пионеры?»

Для того чтобы показать учащимся отличие задачи нового типа от задач, раскрывающих смысл операции сложения, возможно, имеет смысл одновременно рассмотреть и такую задачу: «Возле школы пионеры посадили З клена и 2 липы. Сколько всего деревьев посадили пионеры?» Учитель кратко записывает условие обеих задач:

Обсуждаются сходство и различие условий и требований этих задач.

Для задачи нового типа учитель выполняет иллюстрацию, например, на наборном полотне (рис. 55). Одновременно учащиеся могут работать с индивидуальным наглядным материалом. Этот процесс комментируется. Так, в частности, отмечается, что поскольку

количество лип неизвестно, то в

соответствующий кармашек устанавливается полоска. «За ней, говорит учитель,—— находятся кружки, изображающие липы. В тот же

кармашек помещаются два кружка, ведь лип было на две больше, чем кленов. Сколько же кружков за полоской? Столько же, сколько кленов». Итак, количество лип в наборном полотне изображается тремя. и двумя кружками. Проделанная практическая работа описывается числовым выражением: З + 2.

Следующую задачу ученики могут проиллюстрировать самостоятельно, не прибегая к полоске. Используется уже известный прием:

если множество А содержит а кружков, а множество В— на Ь кружков больше, то в один кармашек укладывается а кружков, а в другой столько же и еще Ь.

Таким образом, отношение «больше на» сначала переводится на язык множеств — «столько же и еще», а потом на язык числовых выражений — записывается в виде суммы.

Методика обучения учащихся решению задач на уменьшение числа на несколько единиц аналогична рассмотренной. Отношение меньше на» с помощью иллюстраций истолковывается на языке множеств как «столько же, но без...». Пусть, например, рассматривается задача: «Пионеры посадили возле школы 5 лип, а кленов на З меньше. Сколько кленов посадили пионеры?» На наборном полотне описанная в задаче ситуация моделируется так: кленов столько же, сколько лип, но без трех, т. е. удаляется часть множества. Такой операции, как хорошо известно учащимся, соответствует арифметическая операция вычитания.

При обучении решению задач данного типа также большое значение имеет упражнение учащихся в составлении задач по данным выражениям.

Задачи на сравнение численности двух множеств с помощью вычитания (задачи на разностное сравнение). Выше была описана система подготовительных упражнений для задач на увеличение (уменьшение) числа на несколько единиц. Эти упражнения закладывают основу и для задач данного типа. Вместе с тем у задач на разностное сравнение есть и особенности.

Рассмотрим две задачи: «Помогая колхозу, школьники пропололи 5 грядок свеклы и 4 грядки моркови. Сколько грядок пропололи школьники?»; «Помогая колхозу, школьники пропололи 5 грядок свеклы и 4 грядки моркови. На сколько больше было прополото грядок свеклы, чем моркови?» Эти задачи относятся к разным типам. Первая - на раскрытие смысла сложения, вторая -- на разностное сравнение. Однако условия у этих задач одинаковы, различаются только требования. Задачи первого типа учащимся хорошо известны. Поэтому можно предположить, что некоторые ученики, поверхностно ознакомившись с текстом задачи на разностное сравнение, могут решить ее так же, как раньше решали задачи, раскрывающие смысл сложения. Поэтому, вероятно, полезно рассмотреть кратко записанные формулировки задач обоих типов одновременно, сравнить их, выявить сходство и различие:

Свекла —- 5 гр. Свекла — 5 гр.

Морковь — 4 гр. Всего ? гр. Морковь — 4 гр.

На сколько свеклы больше?

Возможно также, что некоторые учащиеся истолкуют слова «на... больше» в том смысле, который вкладывался в них в задачах на увеличение числа на несколько единиц, т. е. попытаются решить задачу нового типа сложением. Чтобы обосновать выбор действия для решения задачи на разностное сравнение, ее сначала нужно решить на предматематическом уровне.

На наборном полотне иллюстрируется условие задачи (рис. 56).

Чтобы ответить на вопрос задачи, из кармашков попарно удаляются

«грядки» свеклы и моркови. Таким образом, из множества, содержащего 5 элементов («грядок» свеклы), удалено подмножество, со

держащее 4 элемента (столько

«грядок» свеклы, сколько было

«грядок» моркови). Это, как хорошо известно учащимся, описывается операцией вычитания: 5 — 4.

Итак, получен ответ: грядок со свеклой на одну больше, чем грядок с морковью.

Разностное сравнение, в которых требуется найти «на сколько... меньше?»

для закрепления умения решать задачи данного типа большое значение имеют упражнения на составление текстовых задач по кратко записанному условию, чертежу, иллюстрации, числовому выражению.

Задачи, раскрывающие смысл понятия умножения. Методика введения понятия умножения достаточно подробно описана в § 15, посвященном изучению концентра «Сотня». Ограничимся несколькими замечаниями общего характера.

Умножение в начальной школе определяется через сложение. Произведение а• Ь рассматривается как сумма, состоящая из Ь слагаемых, каждое из которых равно а. Поэтому умножение можно рассматривать на более высоком уровне абстракции, чем сложение и вычитание. действительно, понятия сложения и вычитания формировались у учащихся следующим образом: сначала рассматривались определенные, интуитивно ясные операции над множествами предметов различной природы; эти операции описывались на математическом языке суммой или разностью; в результате многократного выполнения всех этих действий школьники убеждались, что смысл математических выражений не зависит от свойств предметов, составляющих множества. для определения умножения совсем не обязательно обращаться к предметным множествам. Можно рассмотреть понятие суммы (абстрактное понятие) и, отвлекаясь от конкретных значений слагаемых, прийти к абстракции более высокого порядка — понятию произведения. Схематически это можно изобразить так:

Учителю такая идея введения умножения может показаться соблазнительной: не нужно тратить время на работу с иллюстрациями, наглядностью. Учитель может просто взять какую-либо задачу, например: «Купили З коробки карандашей. В каждой коробке было по 5 карандашей. Сколько всего карандашей купили?» По ней учащиеся в состоянии самостоятельно составить выражение известного им вида: 5+5+5. Затем учитель объявляет, что сумму, в которой слагаемые одинаковы, можно записать иначе: 5. 3. Одновременно ученикам сообщается соответствующая терминология — «умножение», «произведение», «множитель», демонстрируется знак умножения. Остается только закрепить новые сведения в процессе их многократного использования при решении задач.

Однако описанный подход выглядит привлекательно только на первый взгляд. Формирование понятия произведения не самоцель. Оно используется в дальнейшем для изучения других, более сложных понятий — частного, отношений «больше в ... раз», «увеличить в ... раз» и других. Если у учащихся после изучения умножения останется только определение этой операции и сопутствующая терминология, то пользы от этих знаний в дальнейшем будет немного. Важно, чтобы учащиеся, усваивая понятие произведения, приобрели опыт работы с предметными множествами, который пригодится им в дальнейшем.

На рис. 57 отражено содержание предматематического решения задачи о карандашах, приведенной выше.

Задачи, раскрывающие смысл

операции деления, В § 15 обсуждалась проблема обучения учащих ся делению, Однако вопрос о том, как раскрыть учащимся смысл этой операции, остался открытым.

Операция деления для школьников является самой сложной.

Это объясняется следующими

причинами. Деление — операция,

обратная умножению, поэтому

было бы естественным определить ее через умножение. Так, например, делается в вузовском курсе математики: частным целых неотрицательных чисел а и Ь (а Ь, Ь О) называется такое целое неотрицательное число с, что а = Ьс. Для учащихся начальной школы такое определение неприемлемо. Действительно, трудно себе представить, как его можно было бы интерпретировать на предматематическом уровне — на языке множеств, например.

Отметим, что некоторые специалисты придерживаются на этот счет другого мнения. Например, в одном из учебников математики для III класса (А. С. Пчелко и др.; М., 1985) деление определяется следующим образом: Разделить 48 на 4 — значит, найти число, которое при умножении на 4 дает 48. Это число 12. Значит, 48:4= i2э.

Кроме того, определять деление через умножение методически нецелесообразно, поскольку умножение в отличие от сложения и вычитания для учащихся новая, мало изученная операция.

Таким образом, проблема введения понятия частного состоит в выборе предматематической интерпретации его смысла. Это должно позволить учащимся использовать хотя бы в некоторой степени знания и умения, сформированные при изучении действий первой ступени.

Житейские ситуации, описываемые выражением а: Ь, могут иметь двоякий смысл. Так, выражению $:4 могут соответствовать, например, такие текстовые задачи: На 4 тарелки разложили поровну 8 яблок сколько яблок оказалось на каждой тарелке?»; «Было

8 яблок. Их разложили по 4 в каждую тарелку. Сколько для этого потребовалось тарелок?» В первой задаче выражение 8:4 соответствует количеству яблок в тарелке, во второй задаче — количеству тарелок с яблоками. Очевидно, что эта особенность деления должна быть отражена на предматематическом уровне.

Рассмотрим один из возможных вариантов методики обучения учащихся решению задач, раскрывающих смысл операции деления.

Сначала выясним, что представляет собой деление некоторого числа на равные части с предматематической точки зрения. Предположим, что имеется некоторое множество предметов, например 12 кружков, и их необходимо разложить поровну в З кармашка наборного полотна. Спрашивается, сколько кружков окажется в каждом из этих кармашков? Практически эта задача решается следующим образом. В каждый из трех кармашков укладывается по одному кружку. Если в исходном множестве остались кружки, то в каждый кармашек укладывается еще по одному кружку, и так поступают до тех пор, пока не будут разложены все кружки. Для того чтобы ответить на вопрос задачи, можно поступить двояко:

либо посчитать, сколько кружков оказалось в одном из кармашков, либо вспомнить, сколько раз выполнялась операция по раскладыванию кружков. В любом случае выполненное вручную деление на математическом языке можно описать с помощью разности: 12 —

— З — З — З З. Вычитаемые в этой разности показывают, сколько кружков попадало в наборное полотно в результате однократного выполнения операции раскладывания кружков. Число, соответствующее количеству вычитаемых, и есть ответ на вопрос задачи.

Совсем по-другому решается задача на деление по содержанию. Дано некоторое количество кружков, например 12. Нужно разложить их по З в какдый кармашек наборного полотна и определить, сколько для этого потребуется кармашков. Практическое решение этой задачи на языке математики также описывается разностью:

12 —3 — З — З З. Это выражение с точки зрения математики не отличается от рассмотре4ного выше, однако предматематический его смысл совершенно иной. Каждое вычитаемое соответствует количеству кружков, попадавших одновременно в один кармашек; количество вычитаемых соответствует количеству заполненных кармашков.

Рассмотренная интерпретация операции деления позволяет использовать для разъяснения смысла деления хорошо известную учащимся операцию вычитания. Она дает возможность также раз- граничить деление на равные части и деление по содержанию.

Обратимся теперь собственно к методике обучения учащихся решению задач нового для них типа.

Вначале, очевидно, целесообразно рассмотреть процесс деления, производимый реально. К доске, например, вызываются 5 учеников. Одному из них учитель дает мешочек («корзину») с кружками («яблоками»). Предлагается раздать «яблоки» поровну остальным ученикам. Число кружков в мешочке кратно 4. Обращается внимание школьников на то, что количество «яблок», которое получит каждый ученик, неизвестно. Процесс деления «яблок» естествен

каждый ученик получает сначала по одному «яблоку», затем еще по одному и т. д.

Аналогичное задание можно предложить всем учащимся. При этом они должны использовать индивидуальные наборные полотна. Например, нужно разложить 15 «виден» на 5 «тарелок» поровну. Подводя итог этой работы, учитель показывает, как выполненную вручную операцию описать математически: 15:5=3. Вводятся термины «делимое>, «делитель», «частное».

Возможно, что целесообразно сразу же (для контраста) рассмотреть процесс деления, имеющий другой смысл. К доске вызывается ученик. Он тоже получает мешок с кружками. Ему предлагается разделить «яблоки» так, чтобы каждый ученик получил по 4 «яблока». Теперь внимание класса акцентируется на том, что неизвестно, сколько учеников получат «яблоки». Ученик у доски отсчитывает по четыре «яблока» и раздает их товарищам.

Затем организуется индивидуальная работа детей. Они должны разложить 15 «виден» по 5 в каждую «тарелку», используя наборные полотна. Учитель показывает, как выполнить соответствующую математическую запись.

В заключение полезно обсудить с учащимися общее и особенности в работе над задачами двух рассмотренных видов.

И в первой и во второй задачах дано одинаковое количество вишен (15), и эти вишни нужно разложить поровну в тарелки. Однако в первой задаче сказано, сколько всего тарелок (5). При этом неизвестно, сколько вишен окажется в каждой из них. Поэтому вишни раскладывались по одной. Во второй задаче наоборот, сообщалось, сколько вишен нужно положить в каждую тарелку (5), но спрашивалось, сколько потребуется тарелок. Чтобы ответить на этот вопрос, вишни раскладывались группами (по 5).

Такое обсуждение дает возможность еще раз уточнить смысл компонентов в полученных равенствах

Сформированные у учащихся представления о делении закрепляются в процессе решения простых задач. Если у кого-либо из учеников возникнут затруднения, ему можно предложить проиллюстрировать решение задачи с помощью наборного полотна.

Большое значение для осознания детьми смысла деления имеют упражнения на составление задач по данным частным, причем когда по выражению нужно составить две задачи — на деление по содержанию и деление на равные части.

Задачи, раскрывающие связь между умножением и делением. Изучение операций умножения и деления во взаимосвязи обеспечивает качественное усвоение учащимися обеих операций. На практике это может достигаться разными способами.

Задачи на умножение и деление предлагаются в системе: одна задача решается умножением, а две другие, обратные ей по структуре,— делением. Задачи могут иметь разный сюжет. Например:

«Купили 4 банки с краской. В каждой банке по З кг краски. Сколько всего краски купили?»; «Купили 27 кг картофеля; он разложен поровну в 9 пакетов. Сколько картофеля в каждом пакете?»; «В магазин привезли 12 л томатного сока в двухлитровых банках. Сколько привезли банок с соком?»

Учащимся предлагается составить задачи, решаемые умножением и делением, используя, например, слова: «посадили деревья», «в каждом ряду», «всего рядов»; «принесли корзину с морковью>, «каждому кролику дали», «всего было кроликов» и т. д.

После решения задачи ученики должны проверить ее решение с помощью обратной задачи. Причем если данная задача решается делением, то обратная ей должна решаться умножением. Например, исходная задача: «для новогодних подарков купили 16 апельсинов. В каждый подарок положили по 2 апельсина. Сколько подарков приготовили к празднику?» После ее решения (получен, допустим, ответ: 4 подарка) составляется проверочная задача: «для новогодних подарков купили апельсины. Их разложили поровну в 4 подарка по 2 апельсина в каждый. Сколько всего апельсинов купили?»

Кроме перечисленных приемов (здесь перечень их неполон), используются специальные задачи, раскрывающие связь между умножением и делением. Приведем примеры таких задач.

З а д а ч а 24. для школьной столовой привезли 5 одинаковых банок с соком. Всего привезли 15 л сока. Сколько сока в каждой банке?

З а д а ч а 25. для школьной столовой привезли несколько трехлитровых банок с соком. Всего привезли 15 л сока. Сколько банок с соком привезли?

З а д а ч а 26. девять литров сока разлили поровну в банки. Всего получилось З банки с соком. Сколько сока было в каждой банке?

З а д а ч а 27. девять литров сока разлили в несколько банок поровну. В каждой банке оказалось по З л сока. Сколько всего было

банок?

З а д а ч а 28. Некоторое количество сока разлили в З банки поровну. В каждой банке оказалось по З л сока. Сколько всего было

сока?

З а д а ч а 29. Некоторое количество сока разлили по З л в каждую банку. Оказалось З банки с соком. Сколько всего было сока?

Эти задачи, так же как и задачи двух предыдущих типов, решаются либо умножением, либо делением. Однако для них характерна существенная особенность. Рассмотрим, например, задачу 24. По сюжету она напоминает задачи, с помощью которых раскрывался смысл умножения: речь идет о сумме, в которой все слагаемые одинаковы, и о значении этой суммы. Такие задачи, как известно, решаются умножением. Правда, запасать решение задачи 24 с помощью умножения удается, только используя 4ОКОШКО» или букву:

С другой стороны, эта задача решается делением 15: 5. Заметим, что «увидеть» это выражение несколько сложнее, чем уравнение. Итак, содержание задачи 24 можно выразить с помощью уравнения и с помощью выражения. Этот факт убедительно демонстрирует связь между этими операциями.

Очевидно, что решение задач 25—29 также можно выразить и уравнением и выражением. Так, задаче 25 соответствует уравнение 3-х= 15 и выражение 15:3;задачам 26 и 27 —9:х=3 и 9:3; задачам 28 и 29—х:3=3 и 3.3.

Двойственный характер задач 24—29 определяет особенности методики обучения учащихся их решению.

1. у учащихся сформированы знания и умения, необходимые для решения задач, раскрывающих смысл умножения и деления. Чтобы использовать их в полной мере, необходимо показать детям алгебраический смысл содержания задач 24_29*.

2. Поскольку операции умножения и деления используются здесь в необычных условиях, необходимо обратиться к наглядным пособиям.

3. Этим задачам соответствуют уравнения разных типов. Поэтому, вероятно, характер иллюстрации их решения будет различным.

С алгебраической точки зрения задачи 24—29 относятся к разным типам: задачи 24 и 25 — на нахождение неизвестного множителя (а. х—Ь); (х.а= Ь); 26 и 27 — на нахождение неизвестного делителя(а:х=Ь); 28и 29— на нахождение неизвестного делимого (х:а= =Ь).

Рассмотрим один из вариантов методики обучения школьников решению задач этих типов.

Задачи на нахождение неизвестного множителя. Работу над новым материалом можно начать с выполнения следующих заданий. Учащимся демонстрируется трехместный предикат, записанный на доске или выставленный в наборном полотне с помощью «окошек» и математических символов: О О = О.Составляются текстовые задачи. Сначала выбирается сюжет задачи. Затем в предикат подставляются значения множителей, соответствующие сюжету, и, наконец, формулируются условие и требование задачи.

• Иными словами, предлагается вводить понятие уравнения через задачи. Это следует из сформулированного в 18 положения, что в начальных классах любое математическое понятие должно вводиться только через текстовые задачи, такая точка зрения не совпадает с позицией авторов программы по математике для начальной школы (1986), авторов учебного пособия (<Методика преподавания математики в начальных классах М. А. Антовой и Г. В. Вельтюковой. Они полагают, что понятие уравнения должно формироваться непосредственно на основе понятий равенства и переменной. Такой подход отражен в 26 настоящего пособия.

Например, предлагается составить задач о коробках с красками. В «окошки» подставляются числа 4 и 5 5 4 = О. Имея опыт

составления задач по выражениям вида а Ь учащиеся могут сформулировать задачу: «Для урока рисования приготовили 4 коробки с красками. В каждой коробке 5 красок. Сколько всего красок в этих коробках?» Конечно, учащиеся в состоянии решить эту задачу, не обращаясь к наглядности. Однако в интересах дальнейшей работы целесообразно проиллюстрировать ее решение, например, с помощью наборного полотна: в 4 кармашка устанавливаются кружки: по 5 в каждый и т. д.

Аналогично можно составить и решить еще несколько задач. На этом подготовительная работа заканчивается.

Далее учитель создает проблемную ситуацию: он заполняет окошки» предиката необычным образом — О .]= . Спрашивается, можно ли составить задачу по этому равенству (или уравнению). После обсуждения этой проблемы составляется, например, такая задача: «В каждом ряду посажено одинаковое количество деревьев. Таких рядов — 3, всего деревьев — 15. Сколько деревьев в каждом ряду?» Здесь важно обратить внимание учащихся на очень важный момент — истолкование смысла пустого «окошка». Вполне вероятно, ученики скажут, что в каждом ряду было «неизвестное количество деревьев». В этом случае на конкретном примере

нужно пояснить, что, поскольку рассматривается операция умножения, слагаемые должны быть одинаковыми. Поэтому хоть и неизвестно, сколько деревьев в каждом ряду, но их там поровну.

Чтобы решить данную задачу, учащиеся под руководством учителя выполняют практическую работу с иллюстративным материалом. Она может сопровождаться следующим комментарием: «Известно, что было три ряда деревьев. Значит, на наборном полотне придется использовать три кармашка. Всего было 15 деревьев. Отсчитаем 15 кружков.. В задаче не сказано, сколько деревьев в каждом ряду, но известно, что в каждом было одинаковое количество. Поэтому 15 кружков нужно разложить поровну в каждый из трех кармашков». Учащиеся знают, как поступить в таком случае: 15 кружков раскладывают по одному в кармашек. Знают они, и как описывается этот процесс математически — 15:3=5.

В заключение констатируется, что зависать решение данной задачи можно двумя способами: О. 3= 15 или 15:3. Первая запись называется уравнением. Оно может быть записано иначе — х. 3= 15. Формулируется правило его решения.

Ясно, что методика работы над задачами, которым соответствует уравнение а . х = Ь, не имеет принципиальных особенностей.

Задачи на нахождение неизвестного делителя. План обучения учащихся решению задач этого типа может быть таким же, как и задач на нахождение неизвестного множителя. Сначала ученики составляют и решают задачи известного им типа, которые раскрывают смысл операции деления. Затем учитель предлагает составить задачу по необычной записи: : х =, где а, ЬЛТ и аЬ. С помощью наборного полотна демонстрируется процесс предматематического решения задачи нового типа. И, наконец, это решение описывается математически. Остановимся- на содержании практической работы учащихся с наборным полотном, выполняемой под руководством учителя.

Пусть по предложенному учителем уравнению 15: 0=3 детьми составлена такая задача: «Всего было 15 карандашей. Их разложили в несколько коробок. В каждой оказалось по З карандаша. Сколько было коробок с карандашами?»

В соответствии с условием задачи учащиеся отсчитывают 15 кружков и раскладывают их группами по З в кармашки наборного полотна. Такая операция выполнялась при решении задач, раскрывающих смысл деления по содержанию. Поэтому предматематическое решение описывается частным 15:3.

По уравнению 15:0=3 целесообразно составить и другую задачу: «Всего было 15 карандашей. Их разложили поровну в коробки. Получилось З коробки с карандашами. Сколько карандашей положили в каждую коробку?» Выполняется практическая работа, сопровождающаяся, например, таким комментарием: «Известно, что всего было 15 карандашей. Отсчитаем 15 кружков. Карандаши разложили в З коробки. Значит, приготовим З кармашка наборного полотна.. Карандаши разложили в коробки поровну, поэтому раскладываем кружки по одному в каждый кармашек. Таким образом, 15 разделим на З равные части — 15:3=5».

Задачи на нахождение неизвестного делимого. При обучении решению таких задач основные элементы рассмотренной выше методики остаются неизменными. Разница состоит, в частности, в том, что задачи составляются по уравнению 0:5=3, например: «Несколько плодовых кустов посадили по 5 кустов в ряд. Всего оказалось З ряда кустов. Сколько кустов посадили?» «Несколько плодовых кустов посадили в 5 рядов. В каждом ряду — по З куста. Сколько кустов посадили?»

Предматематическое решение первой задачи может комментироваться так: «Сколько всего кружков нужно разложить по кармашкам, неизвестно, но в каждом должно быть по 5 кружков. Причем кружками заполняются З кармашка. Чтобы посчитать, сколько всего кружков в наборном полотне, нужно 5 умножить на 3».

В заключение подчеркнем, что главным в обучении учеников решению задач, раскрывающих связь между умножением и делением, являются предметные иллюстрации, отражающие взаимосвязанность этих операций. При желании учитель может использовать возможность обучения детей решению уравнений. В таком случае важная роль отводится заданиям на составление задач по данному уран- нению.

Задачи на увеличение (уменьшение) числа в несколько раз. Приступая к решению задач данного типа, учащиеся часто смешивают их задачами на увеличение (уменьшение) числа на несколько единиц. Это, пожалуй, единственная серьезная проблема, с которой сталкивается учитель. Поэтому методика должна быть ориентирована на противопоставление задач этих двух схожих типов. Например, учащимся могут быть предложены одновременно две задачи: «У Сережи 4 карандаша, а у Наташи на З карандаша больше. Сколько карандашей у Наташи?»; «У Сережи 4 карандаша, а у Наташи в З раза больше. Сколько карандашей у Наташи?» Еще при ознакомлении учащихся с текстами этих задач учитель предлагает сравнить их условия и требования. Ученики, вероятно, отметят, что числовые данные в условиях обеих задач одинаковы: — 4 и 3; однако в первой задаче число З означает количество карандашей, во второй — «число раз»; в первой задаче сказано «на 3», а во второй — «в З раза»; вопросы в задачах одинаковы.

Учитель кратко записывает условия этих задач, выделяя существенные элементы:

Сережа — 4 карандаша Сережа — 4 карандаша

Наташа —? на З карандаша Наташа —? в З раза больше

Наконец, для каждой задачи выполняются иллюст5ации, например, с помощью наборного полотна. Содержание первой задачи ученики могут проиллюстрировать самостоятельно, для них не должно составлять труда и решение этой задачи, для второй задачи иллюстрацию выполняет учитель (рис. 58). Она служит основой

поиска решения: у Сережи 4 карандаша, а у Наташи «3 раза по столько», значит, у Наташи 12 карандашей (4 ‘3).

Закрепляя навыки решения задач нового типа, полезно чередовать их с задачами на увеличение числа на несколько единиц, упражнять учеников в составлении задач этих двух типов (по выражениям а.Ь и а+Ь), Можно предлагать и задания, например, такого типа: «догадайся, какие слова нужно вставить вместо точек. Составь задачу и реши ее»:

1) рост Сережи в 5 лет —9 дм;

рост Сережи в 7 лет — ? . . . 2 . . . больше.

2) зима — З месяца;

год —? . .. 4 . . . больше.

Таким же образом ученики знакомятся с решением задач на уменьшение числа в несколько раз, т. е. сначала сравниваются тексты и кратко записанные условия этих задач и задач на уменьшение числа на несколько единиц; содержание задач иллюстрируется и описывается на математическом языке; выполняются упражнения на закрепление.

Задачи на сравнение чисел с помощью операции деления (задачи на кратное сравнение). При обучении учеников решению задач данного типа за основу может быть взят методический подход, рассмотренный выше.

Наиболее распространенной ошибкой, которую допускают ученики, является решение задач на кратное сравнение вычитанием, т. е. решение их как задач на разностное сравнение. Для того чтобы предупредить ее, следует с самого начала противопоставить такие задачи. С этой целью ученикам одновременно предлагаются задачи одного и другого типов, выясняется, чем похожи и чем различаются их условия и требования.

Пусть, например, рассматриваются такие задачи: «К кормушке прилетели 8 снегирей и 2 синицы. На сколько снегирей больше, чем синиц?»; К кормушке прилетели 8 снегирей и 2 синицы. Во сколько раз снегирей больше, чем синиц?» Дети наверняка заметят, что в этих задачах одинаковые условия. Различаются только требования:

в первой задаче спрашивается «на сколько», а во второй «во сколько раз». Эту особенность можно подчеркнуть при краткой записи содержания задач.

Следующий этап работа с иллюстративным материалом. Она имеет особое значение при решении задач на кратное сравнение. Весьма вероятно, что умение решать задачи на увеличение числа в несколько раз некоторые ученики могут попытаться использовать в новой ситуации, рассуждая, например, так: «Чтобы увеличить число в несколько раз, нужно выполнить умножение. В задаче о снегирях и синицах говорится: «во сколько раз больше», значит, эта задача решается умножением».

На наборном полотне выполняется иллюстрация для первой задачи. Ученики делают это самостоятельно. Известным образом эта иллюстрация преобразуется, и записывается соответствующее математическое выражение: 8—2. Иллюстрацию ко второй задаче предлагает учитель (рис. 59). «Чтобы ответить на вопрос, во сколько

раз снегирей больше, чем синиц,— объясняет учитель,— нужно определить, сколько раз по 2 содержится в 8». Получить ответ на вопрос задачи можно и практически убирать кружки, обозначающие снегирей, по два и затем посчитать, сколько раз это удалось сделать. Учащимся известно, что на языке математики это означает: 8:2=4.

В заключение подчеркивается, что, решив данную задачу, получили и ответ на вопрос: во сколько раз синиц меньше, чем снегирей.

Выше был рассмотрен лишь один из возможных вариантов методики обучения учащихся решению задач на кратное сравнение. Вероятно, изучение этой темы можно было бы начать с рассмотрения задачи, обратной задаче на увеличение (уменьшение) числа е несколько раз. Однако в любом случае роль иллюстраций является определяющей.

Другие важнейшие типы простых задач. Традиционным для программы по математике для начальных классов являются понятия д о л и и д р о б и. Не исключение и программа 1986 г. Необходимость знакомства младших школьников с этими понятиями естественна, поскольку с операцией деления предметов, множеств предметов и величин на равные части, со словами «половина», «треть», «четверть» дети часто сталкиваются в быту. Важная роль в формировании представлений о доле и дроби принадлежит текстовым задачам.

Из вузовского курса математики известно, что понятие дроби связано с расширением кольца целых положительных чисел до поля положительных рациональных чисел. Рассматривались два подхода к такому расширению аксиоматический и на основе измерения длины отрезка. Положительным рациональными числом назывался класс эквивалентных упорядоченных пар натуральных чисел или класс эквивалентных дробей. На множестве определялись операции, доказывались их Свойства.

Программой 1986 г. не предусмотрено изучение младшими школьниками операций на множестве обыкновенных дробей, поэтому формирование у них представлений о дроби как о числе невозможно. Первоначальные Сведения о дробях учащиеся должны получить через практические действия над реальными объектами, геометрическими фигурами, величинами Таким образом, методическая проблема знакомства учащихся с дробями состоит в выборе учителем целесообразного множества исходных объектов и практических операций, которые ученики будут выполнять над ними. Понятие дроби будет отождествляться с результатом этой операции.

Для решения этой проблемы можно воспользоваться определением рационального числа через измерение длины отрезков. (Конечно, не подходом в целом, а лишь некоторыми его элементами.)

Начнем с содержания практической процедуры, результат которой дети будут математически описывать обыкновенной дробью. Она имеет много общего (но не совпадает) с процессом измерения длины отрезка. Если некоторый объект А удается разделить на Ь равных частей и взять а таких частей, то результат этой операции можно выразить так: получена -- часть объекта А. Допустим, А характеризуется каким-либо свойством, например длиной, которое выражается числом п(А). Тогда результат описанной операции над А выразится числом С = п(А):Ь . а. Это число показывает, какую длину имеет

часть объекта А. Такое представление о дроби имеет ряд существенных особенностей. Например, с точки зрения ученика, символ не имеет Смысла, так как непонятно, что именно разделено на 4 равные части. У выражения «{. яблока» или «- отрезка АВ>? смысл есть: яблоко или отрезок АВ разделены на 4 равные части, и взята одна такая часть. Как следствие, учащиеся не смогут осознанно

ответить на вопрос: какая из дробей больше: 4- или —-. Такие ВООСЫ в начальных классах вообще некорректны. Пытаясь ответить на них, ученики могут прийти к удивительным «открытиям», которые негативно повлияют на усвоение соответствующего материала в средних классах. Например, дети могут «установить», что 4-.с-- (ведь половина яблока меньше трети арбуза!) или что

(если сравниваются доли сливы и яблока). другое дело, если вопрос формулируется так: «Что больше: 4- или 4- отрезка АВ?»;

«Что больше: -- или 4- яблока?» и т. д. Сравнение чисел, представленных в виде дроби, возможно только в У классе, после того как определится их место на числовом лучё, выяснится смысл арифметических операций на множестве таких чисел.

дидактически нецелесообразно также рассматривать с учащимися неправильные дроби. Их смысл может показаться детям загадочным. Например, 4 отрезка АВ означает, что этот отрезок разделили на З равные части и взяли 4 такие части. Непонятно, откуда взялась четвертая часть!

Рассмотренная выше операция определяется на множестве объектов, которые учащиеся младшего возраста способны разделить на равные части. Это любые предметы, которые можно изобразить в виде геометрических фигур, «хорошо» делящихся на равные части практически,— отрезков, прямоугольников, квадратов, кругов.

Процедура получения - части А состоит из двух операций —деления А на Ь равных частей и получения а таких частей. Поэтому формирование у учеников понятия дроби начинается с изучения долей.

Изучение темы «доли» можно предварить беседой. Учитель и ученики проводят примеры житейских ситуаций, связанных с практическим делением предметов на равные части. Например, два друга разделили пополам яблоко; 4 одноклассника разделили между собой поровну плитку шоколада и т. д.

Затем организуется практическая работа с вырезанными из бумаги геометрическими фигурами (равносторонними и равнобедренными треугольниками, прямоугольниками и квадратами, равнобедренными трапециями, кругами, моделями отрезков). Соответствующие фигуры имеет каждый ученик. Под руководством учителя дети делят эти фигуры на заданное количество равных частей путем перегибания. Эта работа будет носить творческий характер, если наряду с названными фигурами у учащихся будут и такие, которые разделить на равные части перегибанием невозможно (рис. 60). Выполнение этих заданий способствует пониманию

(на интуитивном уровне, конечно) того, что получить -..- долю фигуры

можно не только делением этой фигуры на равные, но и на равно- великие части.

В процессе такой работы уточняется смысл терминов «половина», «треть», «четверть». Здесь же разъясняется смысл записей:

Практически решаются и обратные задачи: «Покажи 4- круга, 4- квадрата, 4- отрезка» и т. д. Выполняемые операции комментируются.

Принципиально новым этапом при знакомстве с понятием доли является работа над получением 4-, 4-, 4, 4- долей фигуры. В

самом деле, далеко не всякую фигуру можно разделить на п равных частей перегибанием, если не является степенью 2. для простоты достаточно ограничиться рассмотрением отрезков.

Сначала учеников полезно поупражнять в делении отрезка на З, 5, 6 равных частей «на глаз» с последующей проверкой результата путем перегибания модели. Не лишне показать учащимся, как разделить отрезок на равные части с помощью циркуля (необходимый раствор циркуля подбирается методом проб). Таким образом, они убеждаются, что деление отрезка на равные части иногда совсем не простое дело. Поэтому учеников необходимо ознакомить с другим способом деления отрезка на равные части. Суть его в том, что делится не сам отрезок, а число, которое получается в результате измерения этого отрезка. К такому выводу учеников можно подвести, например, следующим образом. Им предлагается начертить в тетради отрезок длиной 12 клеток, а затем разделить его на 2, 3, 4, 6 и 12 равных частей; отрезок длиной 15 клеток и разделить его на 3, 5, 15 равных частей; прямоугольник со сторонами б и 15 клеток и разделить его на 3, 4, 5 равных частей. Последнее, самое сложное, задание выполняется следующим образом. Учащиеся замечают, что ни одна из сторон не делится на 4 равные части нацело. Поэтому подсчитывается общее количество клеток в прямоугольнике 15. 6. (Хотя с понятием площади и правилом вычисления площади прямоугольника ученики еще не знакомы, догадаться, как проще пересчитать клетки в данном прямоугольнике, не очень сложная задача.) Полученный результат — 80 — делится на 4. Значит,

4- прямоугольника состоит из 20 клеток. Ответ проверяется практически.

Наконец, учащиеся учатся решать текстовые задачи, в которых используется понятие доли.

Практическая работа на предыдущих этапах сводилась к определению доли какой-либо геометрической фигуры или числа, выражающего длину отрезка. Поэтому школьники уже подготовлены к решению задач на нахождение доли числа: (1) <В бригаде 84 рабочих. Комсомольцы Составляют -- всех членов бригады. Сколько

комсомольцев в бригаде?»

Понятно, что представления о доле будут у учащихся более глубокими, если наряду с задачами этого типа будут решаться обратные задачи. Для задачи (1) можно составить две обратные:

(2) <В бригаде 28 комсомольцев. Они составляют .- всех членов бригады. Сколько рабочих в бригаде?»; (3) «В бригаде 84 рабочих.

Среди них 28 комсомольцев. Какую долю рабочих составляют

КОМСОМОЛЬЦЫ?»

Чтобы при решении этих задач ученики могли использовать имеющиеся у них знания, учитель должен показать, как перевести их содержание на язык геометрических фигур. Используется методика работы по образцу: учитель с пояснениями выполняет чертежи в соответствии с условиями задач, учащиеся воспроизводят их у себя в тетрадях. Таким образом учащиеся приобретают опыт иллюстрации задач с помощью чертежей. Это позволит им в дальнейшем выполнять такую работу самостоятельно.

Поиск решения задачи (1) осуществляется, например, следующим образом. Строится отрезок АВ, обозначающий количество всех рабочих бригады (рис. 61, а). Комсомольцы, по условию задачи, составляют 1/3 всех рабочих, поэтому АВ делится на З равные части. Отрезок АС соответствует количеству комсомольцев; АВ — количеству членов бригады (84), значит, отрезку АС соответствует 84:3, или 28 человек.

План решения задачи (2) также вырабатывается в процессе построения чертежа (рис. 61, 6). Пусть количеству комсомольцев соответствует отрезок АС. Тогда отрезок, соответствующий количеству всех рабочих бригады (АВ), будет в З раза больше АС. Значит, всего в бригаде 28. 3, или 84 рабочих.

Выполняя чертеж к задаче (3), учитель конкретизирует требование задачи: если исходный отрезок АВ (рис. 61, в) соответствует 84 рабочим, то каким по длине будет отрезок АС, соответствующий количество комсомольцев (т. е. где на отрезке АВ поставить точку С)? Это определяется арифметически — 84:28=3. Число З показывает,

сколько раз по 28 содержится в числе 84. Значит АВ нужно разделить на З равные части. Одна из них и соответствует количеству комсомольцев в бригаде. При делении отрезка на равные части получаются, как известно, доли этого отрезка. В данном случае

Это и есть ответ на вопрос задачи.

Достаточно подробное обсуждение вопросов, связанных с понятиями доли и дроби, избавляет нас от необходимости останавливаться на методике изучения дробей в начальной школе. Отметим лишь, что программой предусмотрено обучение учащихся решению задач только одного типа -— на нахождение дроби числа.

Понятие функция является одним из фундаментальных математических понятий. Большое внимание его формированию уделяется в курсе математики средней школы, В младших классах возможности для формирования у учащихся представлений о функциональных зависимостях весьма ограничены. Однако такие возможности есть, и учитель обязан их использовать.

/ Одними из простейших видов функциональных отношений явля4тся прямая и обратная пропорциональные зависимости. Из вузовского курса математики известно, что если одна из трех величин равна частному двух других и ее значения постоянны, то значения двух других меняются прямо пропорционально. Если же одна из трех величин равна произведению двух других и ее значения постоянны, •то две другие величины связаны обратно пропорциональной зависимостью.

В начальной школе учащиеся должны получить первые представления об этих зависимостях. И вовсе не потому, что эти зависимости сравнительно просты, а потому что они имеют важное общеобразовательное значение. В самом деле, пропорциональные величины широко представлены в окружающей детей действительности. Это цена, стоимость, количество товара; скорость, расстояние, время движения; выработка в единицу времени (норма выработки), общая выработка, время работы; урожайность, урожай, площадь, с которой он собран; общая масса одинаковых предметов, масса одного из них, количество этих предметов и т. д. Естественно, что с этими величинами учащиеся знакомятся через задачи.

К обучению решению простых задач, раскрывающих связи между пропорциональными величинами, приступают после того, как ученики усвоили смысл операций умножения и деления. Знакомство с названными тройками величин не совпадает по времени. Например, представления о цене и стоимости учащиеся получают гораздо раньше, чем о скорости, урожайности, урожае. действительно, чтобы перейти к рассмотрению понятия «урожайность», необходимо сначала сформировать у учащихся понятие площади, познакомить с мерами массы и площади; чтобы раскрыть смысл понятия скорости, нужно, чтобы ученики знали единицы времени.

Простые задачи с пропорциональными величинами решаются умножением и делением и принадлежат к хорошо известным учащимся типам. Однако, встречаясь с новыми величинами, дети могут испытывать определенные трудности.

Рассмотрим несколько задач на пропорциональность, относящихся к одному типу (задачи, раскрывающие смысл умножения).

З а д а ч а 30. За каждую тетрадь заплатили З к. Купили б таких тетрадей. Сколько стоила покупка?

З а д а ч а 31. Одна табуретка стоит 8 р. Купили 4 такие табуретки. Сколько денег за них уплатили?

З а д а ч а 32. Пионерский отряд находился в пути 3 ч. За каждый час отряд проходил 4 км. Какое расстояние прошли пионеры?

З а д а ч а 33. С каждого гектара колхозного поля собрали по 21 ц пшеницы. Площадь этого поля 5 га. Сколько всего пшеницы собрали?

Учащиеся уже знакомы с краткой записью условий задач данного типа. Поэтому условия задач 30—33 можно записать сначала «традиционно». Например:

Одновременно учитель объясняет, например, что в задаче 30 сказано, что «за каждую тетрадь заплатили З к.», а в задаче 31— что «одна табуретка стоит 8 р.» И в том и в другом случае речь идет о стоимости одного предмета. (<Гораздо короче и грамотнее,— говорит учитель—в таких случаях пользоваться словом «цена»:

цена тетради З к., цена табуретки 8 р.»

Возможно, что, решая задачи, ученики будут испытывать затруднения в выборе необходимого действия. В этих случаях задачи иллюстрируются чертежами (на рис. 62 представлены чертежи к задачам 30, 32, 33). Использование для иллюстраций наборного полотна и предметных множеств нецелесообразно и неэффективно.

Аналогично организуется работа над задачами с пропорциональными величинами, решаемыми делением. (.— далее у учащихся отрабатывается умение определять цену по

данной стоимости и количеству, стоимость по данной цене и количеству и т. д.; скорость по данному расстоянию и времени, время по данному расстоянию и скорости и т. д. С этой целью полезно использовать, например, такие упражнения:

Каждая строка таблицы соответствует отдельной задаче. Рассмотрим методику работы над такими упражнениями на примере первой таблицы. Сначала выясняются общие особенности задач, представленных в таблице: цена постоянная, стоимость увеличивается, неизвестно количество купленного товара Задачи решаются, и таблица соответствующим образом заполняется. Анализируются результаты проделанной работы. Числовые значения в третьей колонке возрастают. На вопрос учителя: «Почему?» ученики могут ответить, например, так: «Потому, что стоимость увеличивается». Такой ответ учителя удовлетворить не должен. Поэтому учащимся предлагается еще одна «задача»: Цена 10, стоимость 40; определить количество. Стоимость увеличилась с 30 до 40, а количество тем не менее уменьшилось. Причина этого в изменении цены. Итак, констатируется: если цена постоянна, а стоимость увеличивается, то количество увеличивается тоже. Наконец, на основании наблюдений, над изменениями значений величин, представленных в таблице, делается более глубокий вывод. Пусть, например, рассматриваются первая, третья и четвертая строки таблицы. Несложно заметить, что стоимость увеличивается соответственно в 2 и З раза. Соответствующие значения количества также увеличиваются, причем в такое же число раз. Такой уровень представлений о пропорциональности для начальной школы вполне достаточен. По такой же методике и на таком же уровне раскрываются прямая и обратная пропорциональная зависимости и между другими величинами. Эти представления не могут быть, конечно, сформированы в результате однократного выполнения рассмотренных упражнений. Они должны использоваться учителем систематически, допустим, в рамках устного счета. Опыт показывает, что работа над ними не занимает много времени и хорошо сочетается с отработкой вычислительных навыков. -

2. ОБУЧЕНИЕ УЧАЩИХСЯ РЕШЕНИЮ СОСТАВНЫХ ЗАДАЧ Прежде всего остановимся на проблеме: что значит у м е т ь р е ш а т ь составные задачи. История методики обучения математике свидетельствует, что данная проблема на разных этапах развития науки решалась по-разному. На рубеже ХIХ и ХХ вв. под умёнием решать задачи понимали способность ученика решать составные задачи вполне определенных типов, так называемые типовые задачи, регламентированные программой. Для этого ученика вооружали четко ограниченным множеством специальных методов (правил) Каждый из них соответствовал задачам определенного типа. Как . свидетельствует 2, И. Шохор-Троцкий, весьма известный в те времена методист, <На гимназических испытаниях зрелости предлагались по предмету арифметики задачи, из которых каждая требовала непременного знания по возможности большего количества приемов решения задач разного рода* А перечень таких методов был весьма велик: простое тройное правило и сложное, правила процентов, учета векселей, нахождения средних процентных такс, вычисления сроков платежей, цепное правило, правила пропорционального деления, нахождения неизвестного по двум разностям, вычисления пробы, смещения первого и второго рода, сплавов, замены данных, уравнивания данных и т. д. Корни такого понимания умения решать составные задачи уходят в далекое прошлое. В учебниках Х1I1-ХiУ вв. число правил, которыми должны были владеть умеющие решать задачи. было огромным что ни задача, то специальное правило. (Заметим, что среди них были правила с довольно экзотическими названиями: «правило нашедшего кошелька, «правило девиц», правило слепого.) Такая концепция имела серьезных противников в лице С. И. Шхор-Троцкого, Ф. А. Эрна и др. Однако она продолжала господствовать в методике начального обучения вплоть до середины ХХ в. В советской начальной школе до реформы 1968 г. умение решать задачи отождествлялось с умением решать типовые задачи. Число правил, подлежащих усвоению, было достаточно велико. В их числе уже упоминавшиеся правила смешения и сплавов, тройные правила, правила исключения неизвестного, пропорционального деления и т. д. В программе 1968 г. количество типовых задач было резко сокращено. Выделялись только два типа задач: решаемых приведением к единице и на пропорциональное деление. Программой 1986 г. обучение школьников решению типовых задач не предусмотрено. Учащиеся «должны постепенно овладевать простейшими общими подходами к решению задач». Такая концепция является весьма серьезным достижением отечественной методики. Об общих приемах работы над задачей, которыми могут овладеть младшие школьники, подробно говорилось в § 19. Там же были рассмотрены общие вопросы методики формирования этих приемов. Поэтому остановимся на важном следствии из современной концепции обучения решению составных задач: учитель должен проявлять творческую инициативу в разработке системы составных задач; целесообразность этой системы определяется следующим условие обеспечивает ли она усвоение учащимися общих приемов работ над задачей? Творческая активность учителя в этой области имеет большое значение для развития умственных способностей учащихся и подготовки младших школьников к изучению математики в средних и старших классах. Активная позиция учителя в совершенствовании процесса обучения решению задач должна сообразовываться со следующим требованием. Учитель может предложить учащимся решить задачу, если видит, что ее содержание допускает интерпретации на всех возможных уровнях: с помощью краткой записи, чертежа, предметной иллюстрации и практической работы (подробно об этом сказано в § 19). Причем каждый уровень интерпретации должен быть доступен пониманию учащихся, согласовываться с их знаниями, умениями и навыками.

Рассмотрим задачу: «Определить наименьшее количество носильщиков, с которыми геолог может совершить шестидневный переход через пустыню, если он сам и каждый из носильщиков могут нести лишь четырехдневный запас еды». Очевидно, что кратко записать условие этой задачи школьники не смогут. Очень сложно проиллюстрировать ее содержание графически, следовательно, эта задача не для начальной школы.

Рассмотрим следующую задачу: «Купили два отреза ткани

один по цене б р., а другой 8 р. за метр. Стоимость обоих отрезов одинакова, но в первом было на 2 м ткани больше, чем во втором. Сколько ткани в одном отрезе и сколько в другом?» (отметим, что эта задача сложнее, чем допускалось программой 1968 г.). В данной задаче рассматриваются пропорциональные величины. Поэтому кратко ее условие, как известно учащимся, записывается в виде таблицы:

Можно предвидеть, что этого будет недостаточно, чтобы дети самостоятельно решили задачу, поэтому учитель должен иметь альтернативный вариант интерпретации с помощью чертежа. Если не удаётся придумать чертеж, доступный пониманию детей, предлагать эту задачу учащимся нет смысла. В данном случае чертеж достаточно прост (рис. 63). Из рисунка видно, что несложно опреде

лить, какое число соответствует отрезку СВ: 6- 2= 12 на столько меньше заплатили бы за первый отрез, если бы по длине он был равен второму.

Возможно, что, опираясь на чертеж, учащиеся не смогут самостоятельно решить задачу. Теперь все зависит от способности учителя придумать доступную предметную иллюстрацию. В качестве предметов» могут быть использованы модели отрезков, соответствующие цене одного и другого материала. Отрезки укладываются парами (рис. 64). Ученики могут заметить, что всякий раз, когда от А укладывается «шестирублевый» отрезок, а справа — «восьми- рубленый», разница в стоимости покупок увеличивается на 2 р. Если бы длина первого отреза равнялась длине второго, то разница

в стоимости отрезов, как уже известно, составила бы 12 р.Чтобы это условие выполнялось, нужно уложить б пар отрезков. Итак, идея решения найдена уже на основе предметной иллюстрации. Однако на всякий случай учителем должен быть продуман вариант еще более наглядного представления содержания задачи.

Из рассмотренного примера видно, что доступность решения задачи во многом зависит от профессиональной подготовки учителя. Учитель, умеющий хорошо решать задачи и изобретательно их иллюстрировать, может на каждом уроке использовать более сложные и интересные задачи, чем предлагаемые в учебнике. А это обеспечит более высокий уровень преподавания математики в целом.

Остановимся на еще одном вопросе, связанным с составными задачами,— методике обучения учащихся решению задач в два действия. Особенности этой методики обусловлены причинами психологического характера. Как известно, учащиеся в течение долгого времени решают простые задачи. При этом поиск решения сводится, фактически, к выбору арифметического действия, которое нужно выполнить над двумя числовыми данными, содержащимися в условии задачи. Предположим, учащимся предложена следующая задача:

(1) «У Сережи З тетради, а у Наташи на 2 тетради больше. Сколько тетрадей у Сережи и Наташи вместе? Впервые сталкиваясь с составной задачей, учащиеся могут решить ее неверно. Причем ошибки в решении будут достаточно характерными: 3+2=5 или

3+5=8.

Причина первой. ошибки состоит в том, что ученик попытался решить задачу нового типа так же, как хорошо ему известные задачи, в которых слова «больше на» и «вместе» обусловливали выбор операции сложения. Ученик может рассуждать так: в условии даны два числа З и 2, сказано, что «больше на», значит, задача решается выражением 3+2 (или сказано «вместе», значит, 3+2).

другая ошибка свидетельствует о том, что ученик понимает идею решения задачи, но у него не хватает знаний для правильной реализации этой идеи: он никогда не записывал решение задачи выражением, содержащим два действия.

Чтобы предупредить эти ошибки, можно воспользоваться разными методическими приемами. Например, учащимся одновременно предлагаются две задачи, связанные общим сюжетом: (2) «У Сережи З тетради, а у Наташи на 2 тетради больше. Сколько тетрадей у Наташи?»; (3) «У Сережи З тетради, а у Наташи 2. Сколько тетрадей у Сережи и Наташи вместе?» Задачи таких типов школьникам знакомы, и, решая их, они не будут испытывать трудностей. Затем из задач (2) и (3) конструируется задача (1). Обсуждаются особенности задач (2) и (3), с одной стороны, и задачи (1) — с другой.

Вопросы и задания для самостоятельной работы К. 18 1. Каковы функции текстовых задач в начальном обучении математике? Приведите соответствующие примеры. 2. В чем заключается особенность обучения решению задач в начальных классах?

3. Известно, что текстовые задачи учащиеся начальных классов решают по вполне определенному плану. В чем состоит методика отработки у них соответствующих умений? К § 20 4. Приведите классификацию простых задач, решаемых в ‘—‚У классах. Обоснуйте ее. 5. Опишите методику обучения учащихся решению простых задач, раскрывающих смысл: а) операций сложения и вычитания; б) умножения и деления; в) отношений «больше», «меньше», «равно». б. Назовите особенности формирования у учащихся начальных классов понятий доли и дроби. 7. Раскройте методику обучения школьников решению простых задач, связанных с понятиями доли и дроби. 8. Первоначальные представления о функциональной зависимости формируются у учеников через простые задачи. Каким образом это делается? К § 21 9. Что такое типовые задачи? Какие возможности для обучения учащихся решению составных задач раскрывает современная программа для начальных классов? 10. Объясните, почему для обучения школьников решению задач в два действия требуется специальная методика? В чем состоит ее суть?

23. МЕТОДИКА ИЗУЧЕНИЯ ЧИСЛОВЫХ ВЫРАЖЕНИЙ Понятие математического выражения (или просто выражения), изучаемое в начальных классах, имеет важное значение. Так, это понятие помогает учащимся овладеть вычислительными навыками.

Выясняется, что, решив задачи (2) и (3), фактически решили и задачу (1). Поэтому ее решение записывается так: 3+(3+2). Возможен и другой подход при введении задач в два действия. Рассматривается задача с недостающим данным: У Сережи З тетради, а у Наташи... тетрадей. Сколько тетрадей у Сережи и Наташи вместе?» Ученики согласятся, конечно, что такую задачу решить нельзя — не сказано, сколько тетрадей у Наташи. Учитель, например, говорит, что он не знает, сколько тетрадей у Наташи, но ему известно, что у нее на 2 тетради больше, чем у Сережи. Поэтому сначала вычисляется, сколько тетрадей у Наташи (3+2), а затем — сколько всего тетрадей у детей: 3+2+3. В заключение формулируется полный текст решенной задачи.

УI. ЭЛЕМЕНТЫ АЛГЕБРЫ В НАЧАЛЬНОИ ШКОЛЕ 22. ОБЩАЯ ХАРАКТЕРИСТИКА АЛГЕБРАИЧЕСКОГО МАТЕРИАЛА В КУРСЕ МАТЕМАТИКИ НАЧАЛЬНОЙ ШКОЛЫ достаточно долгое время в психологии господствовало мнение (например, П. П. Блонского), что элементы алгебры следует изучать не в начальных, а в старших классах в силу особенностей мышления младшего школьника, неспособности его к образованию абстракций более высокого уровня. В последние годы исследованиями советских психологов (П. Я. Гальперин, В. В. Давыдов, д. Б. Эльконин и др.) и педагогов (А. И. Маркушевич, А. М. Пышкало и др.) было установлено, что познавательные возможности младших школьников при традиционной системе обучения значительно занижались. дети 6—1О лет при определенной организации обучения могут полноценно усвоить содержание некоторых алгебраических понятий. При этом у них раньше, чем обычно, возникают предпосылки к теоретическому рассуждению (особенно в связи с введением буквенной символики). На основании этого алгебраический материал был включен в программу по математике для начальных классов в 1969 г. Включение в содержание обучения элементов алгебры, особенно упражнений с функциональным содержанием, позволяет увидеть динамичность явлений реального мира, взаимную обусловленность и связь величин, а это оказывает большое влияние на формирование мировоззрения учащихся. Изучение алгебраического материала способствует развитию у учащихся таких логических приемов, как анализ и синтез, обобщение и конкретизация, индукция и дедукция. Введение элементов алгебры .имеет большое значение для совершенствования системы начального математического образования, расширения арсенала математических средств, используемых школьниками при решении задач. Буквенная символика, вводимая в начальных классах, и связанное с ней понятие переменной способствуют обобщению знаний о числах, свойствах арифметических действий. Таким образом проводится работа по функциональной пропедевтике одного из важнейших понятий современной математики понятия соответствия. Использование уравнений для решения задач позволяет существенно изменить всю систему обучения решению задач. В целом же алгебраический материал в курсе математики начальной школы выполняет вспомогательную функцию при изучении основного (арифметического) содержания программы.

действительно, часто вычислительные ошибки связаны с непониманием структуры выражений, нетвердым знанием порядка выполнения действий в выражениях. Усвоение понятия выражения обусловливает формирование таких важных математических понятий, как равенство, неравенство, уравнение. Умение составлять выражение по задаче необходимо для овладения умением решать задачи алгебраическим способом, т. е. с помощью составления уравнений. ‚С первыми выражениями — суммой и разностью — дети знакомятся при I4зучении сложения и вычитания в концентре «десяток». Не используя специальных терминов, первоклассники производят вычисления, записывают выражения, читают их, заменяют число суммой, основываясь на наглядных представлениях. При этом выражение 4+3 они читают следующим образом: «к четырем прибавить три» или «4 увеличить на 3», а выражение 4 — З - «из четырех вычесть три» или «4 уменьшить на 3». Находя значения выражений, состоящих из трех чисел, которые соединены знаками сложения и вычитания, учащиеся фактически пользуются правилом порядка выполнения действий в неявном виде и выполняют первые тождественные преобразования выражений. Познакомившись с выражениями вида а+Ь, первоклассники сначала употребляют термин «сумма» для обозначения числа, получающегося в результате сложения, т. е. сумма трактуется как значение выражения. Затем с появлением более сложных выражений, например вида (а + Ь) с, появляется необходимость иного понимания термина «сумма». Выражение а+Ь называется суммой, а его компоненты — слагаемыми. При введении выражений вида а — Ь, а• Ь, а:Ь поступают аналогично. Сначала разностью произведением, частным) называют значение выражения, а затем само выражение. Одновременно учащимся сообщают названия его компонентов: уменьшаемое, вычитаемое, множители, делимое и делитель. Например, в равенстве 9 — 4 = 5 9 — уменьшаемое, 4 — вычитаемое, 5 — разность. Запись 9 4 также называется разностью. Можно вводить эти термины в другой последовательности: предложить учащимся записать пример 9 — 4, пояснив, что записана разность, и вычислить, чему равна записанная разность. Учитель вводит название полученного числа: 5 — тоже разность. другие числа при вычитании называются: 9 — уменьшаемое, 4 — вычитаемое. Запоминанию новых терминов способствуют плакаты вида

для закрепления этих терминов предлагаются упражнения вида: Вычислите сумму чисел; запишите сумму чисел; сравните суммы чисел (вставьте знак , или= вместо * в запись 4+3 * 5+ 1 и прочтите полученную запись); замените число суммой одинаковых (разных) чисел; заполните таблицу; составьте по таблице примеры и решите их». Важно, чтобы эти поняли, что при вычислении суммы производится указанное действие (сложение), а при записи суммы получаем два числа, соединенных знаком плюс. ‘ На следующем этапе усвоения понятия выражения учащиеся знакомятся с выражениями, в которых используются скобки: (10 — —3)+4, (6—2)+5. Они могут быть введены средством текстов ч. (Соответствующая методика была описаний возможен и другой подход. Учитель предлагает составить на наборном полотне сумму и разность чисел 10 и 3, используя карточки, на которых записаны эти числа и знаки действий. Затем составленную учениками разность 10—3 учитель заменяет подготовленной заранее карточкой с этой разностью. Следующее задание: составить выражение (на этом этапе обучения о нем говорят как о примере), используя разность, число 4 и знак +. При чтении полученного выражения обращается внимание на то, что его компонентами являются разность и число. «Чтобы было заметно,— говорит учитель,— что разность является слагаемым, ее заключают в скобки». Самостоятельно конструируя выражения, дети осознают их структуру, овладевают умением читать, записывать, вычислять их значения. Вводятся термины «математическое выражение» (или просто «выражение») и «значение выражения». Определения этих терминов не даются. Записав несколько простейших выражений: сумм, разностей, учитель называет их математическими выражениями. Предложив вычислить эти примеры, он объявляет, что числа, полученные в результате вычисления, называются значением выражения. дальнейшая работа над числовыми выражениями состоит в том, что дети упражняются в чтении, записи под диктовку, совпадении вычислений, а таблиц, широко используя при этом новые термины. Затем изучается порядок выполнения действий. Выражения вида: 37—24+3, 63:9. 4 знакомы учащимся: они их читали, записывали под диктовку, вычисляли их значения, еще не зная правил порядка выполнения действий, но уже неявно их используя. С выражениями вида а + Ь . с, а— Ь . с учащиеся встречаются впервые. В этом случае может быть создана проблемная ситуация. Учащимся предлагается вычислить значение вьг5Т7 Получив различные значения этого выражения, учащиеся сталкиваются с проблемой: какое же из них считать верным. Разрешая ее, учитель формулирует правило порядка выполнения действий в таких выражениях. Важно подчеркнуть, что при выполнении действий в таких выражениях условились выполнять вначале умножение и деление, а затем сложение и вычитание. Это упрощает запись выражений: произведение и частное записываются без скобок. Чтобы ученики осознанию усвоили правила порядка выполнения действий, наряду с тренировочными упражнениями на нахождение значения выражения полезны специальные задания: «Вычислите с пояснениями (45—3О):5 и 45—30:5; 15. 3—.28:7; расставьте скобки так, чтобы значение выражения равнялось 105». Необходимо сформировать у учащихся еще одно практическое умение читать составные выражения. Вначале, выполняя конкретные операции над множествами, ученики осознают смысл сложения и вычитания как «прибавить» и <вычесть», поэтому выражения они читают следующим образом: «к семи прибавить два», «из пяти вычесть один». В дальнейшем понимание действий сложения и вычитания углубляется. Выражения 7+2, 6— 1 читаются следующим образом: «7 увеличить на 2», «уменьшить на 1». С введением названий компонентов действий эти выражения читаются по-другому: «сумма чисел 7 и 2», «разность чисел б и 1». Затем учащиеся учатся читать составные выражения, в которых действия выполняются в том порядке, в котором они записаны. Так, выражение 4+2+ 1 учащиеся читают: «к четырем прибавить два и к полученному числу прибавить один», а выражение 24:3• 2 «двадцать четыре разделить на три и полученный результат умножить на два». Для чтения сложных выражений учащиеся используют следующий алгоритм: 1) определяют, какое действие в выражении выполняется последним; 2) вспоминают названия компонентов этого действия; 3) называют, чем выражены его компоненты. Для обучения чтению выражений используется методика работы«по образцу». Например, учитель показывает, как читается выражение 3+7: это сумма, в которой первое слагаемое 3, а второе слагаемое — 7. При чтении сложного выражения 16. 4+10 учитель рассуждает так: «В выражении 16. 4+10 последним выполняется действие сложения, значит, это выражение сумма; компоненты этого действия - слагаемые; первое слагаемое выражено произведением, в котором сомножители — числа 16 и 4, а второе слагаемое число 10». (Здесь алгоритм использовался два раза.) Формирование понятия числового выражения тесно связано с обучением учащихся Поясним это на конкретном. примере. Учащимся предлагается условие задачи: «В магазин привезли З ящика помидоров по 10 кг в каждом и б ящиков огурцов по 15 кг в каждом». Условие задачи содержит 4 числовых данных. Вначале ученики выбирают произвольные пары значений и записывают следующие простые выражения, которые можно объяснить исходя из условия задачи: 3+6 —— общее количество ящиков, привезенных в магазин; 10. 3 масса всех помидоров; 15. 6 — масса всех огурцов; б З — на столько больше привезли ящиков огурцов, чем помидоров; 6:3 — во столько раз больше привезли ящиков огурцов, чем помидоров; 15 10 — на столько больше масса одного ящика огурцов, чем ящика помидоров. Затем учитель предлагает учащимся записать сложные выражения, содержащие два и более действий, опираясь на определенные выражения. Выражение 6. 15 —3. 10 соответствует истинному условию и позволяет ответить на вопрос: «На сколько больше привезли в магазин огурцов, чем помидоров? Выражение 15. 6+10. 3 соответствует вопросу: «Сколько всего овощей привезли в магазин?» Составление выражений по условию задачи должно вестись цЦьно с составлением задач по выражению.) С этой целью учащиеся выполняют ряд заданий.

1. у Тани б карандашей, а у Оли 5. Какой вопрос надо поставить к условию задачи, чтобы она решалась так: б - 5. 2. В первый день турист прошел 20 км, во второй день — 14 км. Сколько километров он прошел за два дня? Составьте похожую задачу, которая решается так: 18+ [1. 3. Составьте задачу, в которой надо узнать, во сколько раз 15 меньше 45. 4. Составьте задачу по выражению 18:3. Заметим, что по выражению 18:3 может быть составлена задача на кратное сравнение, на деление по содержанию, на деление на равные части, на нахождение неизвестного множителя. В такой же последовательности проводится работа и со сложными выражениями (составными задачами): 1) поставьте вопрос к усло- нию задачи, чтобы она решалась данным выражением; 2) составьте задачу по выражению, аналогичную только что решенной; 3) составьте задачу данного вида; 4) составьте задачу по выражению. 24. ФОРМИРОВАНИЕ ПОНЯТИЯ ПЕРЕМЕННОЙ Введение буквенной символики, осуществляемое в начальном курсе математики, позволяет познакомить учащихся с основными понятиями современной математики: переменной, урав1ением, неравенством и способствует развитию функционального мышления, так как с понятием переменной тесно связана идея функциональной зависимости. Впервые с упражнениями, раскрывающими понятие переменной, ученики встречаются в первом классе, когда вводятся задания с «окошечками» (пропусками). Окошечко не случайно используется для раскрытия понятия переменной, так как в современной трактовке 1 оно обозначает знак, играющий роль «местодержателя» для имен определенного заданного множества (область значений переменной) -—- множества целых неотрицательных чисел в начальном курсе математики. В учебнике математики для первого класса встречаются записи вида3+О=5;О+О6;5П0О,заданияпокоторьтм могут быть сформулированы в разной теме, например: «Какое из чисел нужно записать в окошечко, чтобы получилась верная запись? Восстанови в записи пропущенное число». Вначале при выполнении таких упражнений используются наглядные пособия. Затем, по мере накопления знаний, учащиеся отказываются от них. Так, при нахождении числа, которое надо вставить в «окошечко» в ‘. записи З + О = 5, предлагается попробовать подставить в «окошечко поочередно числа от О до 4. Вначале такая работа проводится на наборном полотне. Подставляя в «окошечко» карточки с соответствующими числами, ученики выясняют, верна или неверна запись, либо с помощью наглядных пособий, либо опираясь на знание таблиц сложения. Затем примеры такого типа решаются с устным разбором. Раскрытию понятия переменной способствует и работа по заполнению таблиц:

Такие упражнения способствуют не только совершенствованию вычислительных навыков, но и выработке представления о переменной и множестве ее значений. После заполнения таблицы учащимся можно предложить следующие вопросы: какие значения принимает уменьшаемое; вычитаемое; разность? изменяется ли уменьшаемое; вычитаемое; разность? как они изменяются? В некоторых таблицах значения одного из компонентов могут быть постоянными. Таким образом, дети видят, что переменная может принимать не только различные, но и одинаковые значения. Переменная присутствует и в записях вида О + 1, с которыми первоклассники встречаются при изучении различных случаев сложения и вычитания. Следует обратить внимание детей на эти записи и объяснить, что в <окошечко> можно подставлять любое из изученных чисел. Так, при изучении прибавления двух может использоваться запись 0+1+1. Непосредственно перед введением буквенной символики полезно рассмотреть простые арифметические задачи с пропущенными числовыми данными. Подбирая числа, учащиеся получают арифметические задачи, решение которых записывают в виде таблицы (последняя строка таблицы — выражение, являющееся решением задачи). Второй этап формирования понятия переменной — введение букв как символов для обозначения переменной. На этом этапе широко используется сочетание индуктивного и дедуктивного методов, осуществляющее переход от числового выражения к буквенному и от буквенного к числовому, учащиеся тем самым обобщают смысл числовых выражений и конкретизируют его, подставляя вместо букв числовые значения. Для раскрытия смысла букв как символов для обозначения переменной можно использовать однотипные числовые выражения (суммы) и простые односюжетные арифметические задачи. В последнем случае необходимо акцентировать внимание учащихся не на ответе, а на выражениях, соответствующих данным задачи: компонент могут быть различными, но их всегда два, и выражение записывается в виде суммы. На этом этапе учащиеся выполняют разные по форме и содержанию задания. 1. Найти числовые значения буквенных выражений при заданны значениях букв (задание представлено в виде таблицы). 2. Подобрать числовые значения букв, входящих в выражение, значение которого задано. 3. Решить простую задачу с буквенными данными. (Работа над этими задачами осуществляется в такой последовательности: а) в условие подставляются конкретные числовые значения; б) решение этих задач являются числовые выражения; в) буквенные выражения выступают как обобщенная запись решения всех задач с числовыми данными определенного вида.) Аналогично вводится запись разности двух чисел. Однако в этом случае дети учатся устанавливать, какие числовые значения могут

принимать буквы, входящие в разность, что фактически является установлением области допустимых значений переменных. На последнем этапе буквенная символика выступает как средство обобщения знаний учащихся о свойствах действий, взаимосвязям компонентов действий. Обобщение происходит на основе неполной индукции. Учащиеся знакомятся с некоторым множеством однородных выражений. С помощью анализа, сравнения, синтеза они устанавливают общие и существенные свойства этих выражений, т. е. приходят к обобщенным теоретическим знаниям. Поэтому использование буквенной символики как средства обобщения формируемых знаний может осуществляться только тогда, когда учащиеся многократно наблюдали обобщаемые свойства, зависимость, формулировали их и использовали при выполнении различных упражнений. Ученики приходят к пониманию, что использование буквенной символики для записи определенных зависимостей, свойств, отношений означает, что изучаемые зависимости справедливы для любых значений переменных. С этой целью следует предусмотреть’ упражнения, выполняя которые учащиеся овладевают умениями записывать с помощью букв свойства арифметических действий, взаимосвязи компонентов действий, читать свойства и зависимости, записанные с помощью буквенной символики, выполнять тождественные преобразования выражений с переменными на основе знания свойств действий, смысла арифметических действий, доказывать справедливость равенства или неравенства, опираясь на знание элементов теории. Приведем примеры таких упражнений. Для усвоения переместительного свойства умножения можно предложить следующие задания: 1) сравните выражения: 15. 20 и 20. 15, 40. 11 и 11. 40; 2) замените буквы числами так, чтобы получились верные равенства: 23 а=а• 23. При выполнении этого задания учитывается, что одна и та же буква принимает в равенстве одно и то же значение; 3) чему равно произведение 124. 362, если 362 124=44 888? Найдите значение выражения с• т, если т с = 96 (т и с в обоих равенствах одинаковы); 4) закончите запись т . п = п• С целью формирования у учащихся умения доказывать справедливость полученных равенств или неравенств выполняются специальные упражнения. Например, требуется проверить равенство(а Ь) Х Х с=а. с— Ь с или сравнить выражения а:(Ь с)=а:Ь:с. Во всех этих случаях, после того как проведено доказательство, основанное на знании учащимися элементов теории, полезно предложить им убедиться в справедливости равенства или неравенства, придан буквам различные числовые значения. Лучше, если каждый ученик выберет произвольные числовые значения, тогда при проверке можно показать, что вывод, сделанный на основе применения общего правила, верен при любых значениях букв.