Лекция Независимые повторные испытания

Схемой независимых повторных испытаний Бернулли называется схема испытаний, удовлетворяющая условиям:

1. число испытаний n конечно;

2. каждое испытание имеет только два исхода:

а) событие А осуществилось;

б) событие А не осуществилось;

3) все испытания независимы;

4) вероятность р появления события А в каждом испытании постоянна.

Примером повторных испытаний описываемых схемой Бернулли, является многократное подбрасывание монеты.

Теорема: Вероятность появления k раз события А в серии из n независимых повторных испытаний вычисляется по формуле Бернулли:

P _n(k)=C P ^kq ^n-k q=1-P

Частные случаи:

1. Вероятность осуществления события А в n испытаниях равно n раз

P _n (n) =CP ⁿ q ^n-n=P ⁿ q ⁰ =P ⁿ.

2. Вероятность осуществления события А в n испытаниях равно 0 раз

P n (0) =CP ⁰ q ^n-0=q ⁿ=q ⁿ

13

3. Вероятность осуществления события А в n испытаниях не более m раз.

4. Вероятность осуществления события А в n испытаниях не менее m раз .

Пример. Монету подбрасывают n=10 раз . Определить вероятность выпадения “Орла”:

а) ровно 5 раз;

б) не более 5 раз;

в) хотя бы 1 раз.

Решение.

а)

б)

в)

При большом числе испытаний использование формулы Бернулли затруднительно в вычислительном плане. Здесь существенную помощь могут оказать приближённые формулы.

Локальная теорема Муавра-Лапласа.

Если вероятность p осуществления события А в каждом испытании постоянна и отлична от 0 и1, то вероятность того, что событие А появится в n испытаниях равно к раз приближённо равно (тем точнее , чем больше n ) значению функции

при .

Значения функции , соответствующие положительным значениям аргумента x, находятся по таблице. Функция - чётная, т. е.

Пример. Вероятность попадания в цель при одном выстреле равна 0,8 . Определить вероятность того , что при 400 выстрелах произойдёт ровно 300 попаданий .

Решение.

n=400 ; k=300 ; p=0,8 ; q=0,2 ;

Интегральная теорема Муавра-Лапласа.

Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие A появится в n испытаниях от до раз, приближённо равна определённому интегралу.

где

- функция Лапласа. Её значения находятся по таблице. Функция - нечётная, т. е. Для x>5

Пример. Найти вероятность

-15-

Решение.

Вероятность того, что день рождения студента 1 сентября, равна р=1/365.

N=365, k=4, n=1825; =np=1825/365=5.

P1825(4)5⁴/4!*e^-5=p(4, 5)=0, 17547.

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

P(-p)2Ф().

Пример. Вероятность того, что деталь нестандартна, р=0,1.Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности р=0,1 по модулю не более, чем на 0, 03.

Решение. n=400; p=0, 1; =0, 03; q=0, 9.

P( m/400 – 0, 1 0, 03)2Ф(0, 03)= 2Ф(0, 03*20/0,3)=2Ф(2)=2*0, 47725=

=0, 9545.

Смысл полученного результата таков: если взять достаточное число проб по 400 деталей в каждой, то примерно в 95, 45% этих проб отклонение относительной частоты от постоянной вероятности р=0, 1 по модулю не превысит 0, 03.

Случайные величины.

Случайной величиной называется переменная, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее только от случайных причин, которые заранее не могут быть учтены.

Случайные величины обозначаются прописными буквами-X,Y,Z,…, а их возможные значения - соответствующими строчными буквами-x, y, z,…

Функция распределения случайной величины. Х-функция F(X), определяющая вероятность того, что случайная величина Х в результате испытания примет значение,

меньшее х, т.е.

F(x)=P(X x).

Свойства функции распределения.

1. 0 F(x)1;

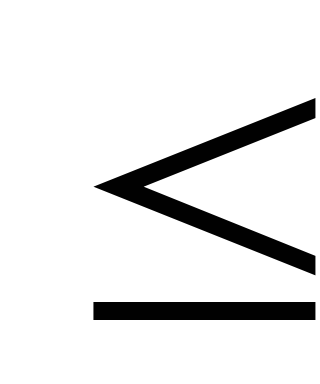2. F(x)- неубывающая функция,F(x1) F(x2) при х1<x2

3. lim_x-F(x)=0; lim_x+F(x)=1.

4. P(x1Xx2)=F(x2)-F(x1).

Функцию F(x) называют также интегральной функцией распределения .

Геометрический смысл функции распределения.

F(x) есть вероятность того, что случайная величина Х примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Х<x

х

График функции распределения называется кумулятой.

Дискретная (прерывная) случайная величина - случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Пример - бросание игральной кости. Случайная величина Х – число выпавших очков.

Способы описания дискретной случайной величины.

1)Закон распределения.

2)Функция --------------

3)Многоугольник ------------.

Закон распределения. дискретной случайной величины – соответствие между ее возможными значениями и их вероятностями.

Обычно задается в виде таблицы, 1-ая строка которой содержит возможные значения дискретной случайной величины, а 2-ая их вероятности.

Х	X1	X2	……………….	хn
Р	P1	P2	…………………	pn

Т.к. в одном испытании случайная величина принимает одно и только одно возможное значение, то события X=x1, X=x2, …….,X=xn образуют полную группу  сумма вероятностей этих событий, т.е. сумма вероятностей 2-ой строки таблицы равна 1:

=1.

ПРИМЕР: Вероятности того, что студент сдаст экзамен в летнюю сессию по математике и психологии, соответственно равны 0.7 и 0,9 . Составить закон распределения числа экзаменов, которые сдаст студент, функцию распределения и построить её график.

РЕШЕНИЕ: Ai-событие, состоящее в том, что студент сдаст i-ый экзамен, i=1,2

Х	0	1	2
Y	P1	P2	P3

P1=P(X=0) =P (=P(

P2=P(X=1)=P(A1A2)=P(A1)P(

P3=P(X=2)=P(A1A2)=P(A1)P(A2)=0,7*0,9=0,63

X	0	1	2
p	0,03	0,34	0,63

0

1

2

0, x  0

0.03, 0 < x  1

F(x)= 0,37, 1< x  2

1, x> 2.

Многоугольник распределения - ломаная, соединяющая точки с координатами (Хi; Рi), i=.

Для предыдущего примера: