Линейная Алгебра КР№1

Министерство образования и науки российской федерации

Федеральное государственное автономное образовательное учреждение

Высшего профессионального образования

Санкт-Петербургский государственный университет

аэрокосмического приборостроения

--------------------------------------------------------------------------------------------------------------------

Линейная алгебра

Методические указания к решению контрольной работы №1

Санкт-Петербург

2012

Составители: Н.А. Вешев, Г.М. Головачев, О.Е. Дик.

Рецензент: доктор физ.-мат. наук, профессор В.Г.Фарафонов

Методические указания к решению контрольной работы № 1 предназначены для студентов 1-го курса технических и экономических специальностей ГУАПа. В пособии содержатся основные теоретические сведения, необходимые при решении задач. Приведены решения характерных задач по модулю “Линейная алгебра”.

Подготовлены к публикации кафедрой высшей математики и рекомендованы к изданию редакционно-издательским советом СанктПетербургского государственного университета аэрокосмического приборостроения.

	Редактор
	Верстальщик
Сдано в набор	Подписано к печати

Формат 60x84 1/16. Бумага офсетная. Печать офсетная. Усл.-печ. Л.

Уч.- изд. Л. Тираж	экз. Заказ №

Редакционно-издательский центр ГУАП

190000, Санкт-Петербург, Б. Морская ул., д. 67

© ГУАП, 2012

1. Комплексные числа 1.1. Понятие комплексного числа. Действия с комплексными числами.

Из курса элементарной математики известно, что существуют

различные числовые множества: множество натуральных	чисел	,
множество целых чисел , множество рациональных чисел	, множество

действительных (вещественных) чисел . Эти множества образуют цепочку вложений

.

Взависимости от того, в каком множестве рассматривается задача, она может иметь разные решения. Например, уравнение x2=2 не имеет решений в

целых числах, т.е. во	множестве . Это же уравнение во множестве
действительных чисел	имеет два решения x		. Возможно расширение
		2

множества действительных чисел до нового множества, которое называется множеством комплексных чисел и обозначается .

При изучении курса линейной алгебры перед студентами ставится задача научиться работать с комплексными числами. В настоящем методическом пособии содержатся примеры решения характерных задач.

Определение. Мнимой единицей i называется такое число, что i2= 1. Заметим, что i не является действительным числом. Тем не менее,

введенное определение приписывает этому символу все свойства числа. Определение. Комплексным числом называется число вида a+bi, где a

и b – действительные числа.

Комплексные числа часто обозначают буквой z. Например, z=3+2i или

z 1 2i .

Определение. Пусть z=a+bi. Число a называется действительной частью числа z, число b называется мнимой частью числа z.

Для обозначения действительной и мнимой частей числа z вводится запись Re и Im: a=Re z, b=Im z. Например, если z=3+2i, то Re z = Re (3+2i)= 3, Im z = Im (3+2i)= 2.

Действия, которые в первую очередь должны быть определены над числами, это сложение и умножение. В случае комплексных чисел они задаются следующим образом.

Определение. Суммой комплексныx чисел z1=a1+b1i, z2=a2+b2i называется число z=z1+z2=(a1+a2)+ (b1+b2)i.

Определение. Произведением комплексныx чисел называется число

z z1 z2 a1a2 b1b2 a1b2 a2b1 i.

Примеры.

(1 2i) (3 4i) 4 6i,

(1 2i) (3 4i) (1 3 2 4) (1 4 2 3)i 5 10i.

Заметим, что если в последнем примере перемножить комплексные числа, раскрыв скобки по известным правилам, и воспользоваться равенством i2= 1, то получится этот же результат.

Возьмем два числа с мнимой частью, равной 0. Пусть z1=a1+0i, z2=a2+0i. Их сумма и произведение тоже будут иметь нулевые мнимые части.

a1 0i a2 0i a1 a2 0i,

a1 0i a2 0i a1 a2 0i.

На основании этого числа с нулевой мнимой частью отождествляют с действительными числами. Иными словами, любое действительное число a является комплексным числом вида a+0i, например, 5=5+0i. Действительные числа являются подмножеством множества комплексных чисел:

.

1.2. Модуль и аргумент комплексного числа. Комплексное сопряжение.

Введем еще несколько определений.

Определение. Модулем комплексного числа называется z a2 b2 . Определение. Аргументом комплексного числа называется число (угол,

				a
cos								,
				z
выраженный в радианной мере), удовлетворяющее условиям				b
sin							.
				z

Решение этой системы определено с точностью до слагаемого 2πk. Принято выбирать значение аргумента, принадлежащее одному из полуинтервалов ( π;π] или [0;2π).

Аргумент обозначается так: arg z= .

Пример. Пусть z

i. Тогда

2 12 2.

3

z

3 i

3

arg

i ;

3

cos 3 ,

2

sin 12 .

arg 3 i 6 .

Заметим, что аргумент положительного действительного числа равен 0, аргумент отрицательного действительного числа равен π, аргумент чисто

мнимого числа	с положительной	мнимой частью равен		.	Например,
				2
arg 5 arg 5 0i 0,	arg( 5) arg 5 0i , arg(2i) arg 0 2i		.
			2
Введем новую операцию над комплексными числами.
Определение. Пусть z=a+bi.		Комплексно	сопряженным		числом к

числу z называется число z a bi .

_____

Пример. 3 5i 3 5i .

Произведение двух комплексно сопряженных чисел равно квадрату модуля каждого из этих чисел: z z (a bi) (a bi) a2 b2 z 2 .

С использованием этого свойства можно получить удобную формулу для деления комплексных чисел.

z1			a1 ib1			(a1 ib1 )(a2 ib2 )					(a1a2 b1b2 ) (a2b1 a1b2 )i
			a ib			(a ib )(a ib )
z	2										a2	b2	.
			2	2		2	2	2	2	2		2

1.3. Комплексная плоскость.

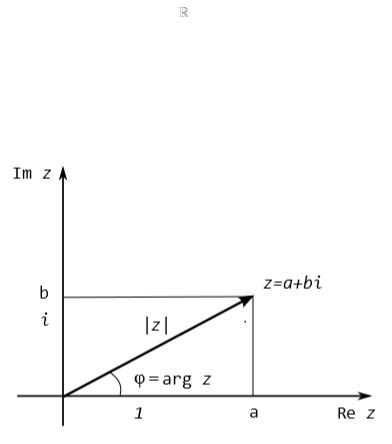
Комплексные числа имеют очень удобную геометрическую интерпретацию. Рассмотрим плоскость, каждой точке которой сопоставлено комплексное число, при этом действительная и мнимая часть числа являются координатами этой точки (Рис. 1). Координатные прямые на плоскости комплексных чисел – это прямые Im z=0 и Re z=0. Прямая Im z=0 – это известная ось действительных чисел . Мнимой единице i соответствует точка, находящаяся на оси чисто мнимых чисел на расстоянии 1 от 0.

Модуль и аргумент комплексного числа имеют очевидный геометрический смысл. Пусть точке A(a;b) соответствует комплексное число z=a+bi. Рассмотрим вектор, проведенный из точки 0 в точку A. Длина этого вектора равна модулю z, а угол, который вектор составляет с положительным направлением, равен аргументу этого числа.

Рис. 1 Комплексная плоскость

Сложению комплексных чисел соответствует сложение соответствующих им векторов (Рис. 2).

2ei 6 .

6

Рис. 2 Сложение комплексных чисел как сложение векторов

1.4. Тригонометрическая и показательная формы записи комплексных чисел. Действия с комплексными числами, записанными в тригонометрической форме.

Представление комплексных чисел в виде z=a+bi называется алгебраической формой записи комплексных чисел. Наряду с этой формой используются еще две формы записи.

Определение. Тригонометрической формой записи комплексных чисел называется представление чисел в виде z z (cos i sin ) r(cos i sin ) , где

введено обозначение |z|=r.

Определение. Показательной формой записи комплексных чисел называется представление чисел в виде z=|z|ei =rei .

Пример. 3 i 2 cos 6 i sin

С использованием этих форм записи произведение двух комплексных чисел приобретает простой вид.

Пусть z1=r1(cos1+isin1), z2=r2(cos2+isin2).

Тогда

z1 z2 r1(cos 1 i sin 1) r2 (cos 2 i sin 2 ) r1 r2 (cos 1 cos 2 sin 1 sin 2 ) i(cos 1 sin 2 sin 1 cos 2 )

r1 r2 cos( 1 2 ) i sin( 1 2 ) .

В последнем равенстве мы воспользовались теоремами сложения аргументов тригонометрических функций. Таким образом, модуль произведения двух комплексных чисел равен произведению их модулей, аргумент произведения двух комплексных чисел равен сумме их аргументов.

Произведение комплексных чисел, представленных в показательной форме, имеет вид

z z1 z2 r1ei 1 r2ei 2 r1 r2ei( 1 2 ) .

Геометрическая интерпретация произведения комплексных чисел показана на Рис. 3.

Рис. 3 Умножение комплексных чисел в тригонометрической форме

Следствием формулы произведения чисел, записанных в тригонометрической форме, является формула Муавра

(cos i sin )n (cos n i sin n ).

В качестве следствия из формулы Муавра получаем формулу возведения комплексного числа в натуральную степень

zn rn (cos n i sin n ).

При возведении числа в n-ю степень его модуль возводится в эту степень, а аргумент умножается на n.

Пример. Вычислим (1 + i)2 двумя способами.

Валгебраической форме (1 + i)2=1+2i+i2=2i.

Втригонометрической форме (1 i)2 2 cos 4 i sin 4 2 2 cos 2 i sin 2 .

При необходимости в последнем равенстве можно выполнить переход от тригонометрической формы записи к алгебраической, подставив значения

синуса и косинуса 2 cos 2 sin 2 2i.

1.5. Извлечение корня из комплексного числа.

Извлечение корня n-й степени из комплексного числа происходит иначе, чем в случае действительных чисел. Соответствующие вычисления удобнее проводить в тригонометрической форме записи. Пусть дано число z=r(cos+isin ).

Число w является корнем n-й степени из числа z, т.е. w nz , если оно является решением уравнения wn=z. Пусть w=ρ(cos+isin ). Тогда

необходимо найти такие модуль и аргумент , что выполнено соотношение

ρn(cosn +isinn)= r(cos+isin ).

Так как модули – действительные неотрицательные числа, то

nr .

Равенство тригонометрических функций приводит к тому, что их аргументы отличаются на целое число периодов: n = +2πk, где k – целое число. Из этого тождества получаем выражение для .

2 k , k 0,1, 2,..., n 1 . n n

Эта формула дает n разных значений для аргумента , которые соответствуют разным значениям k. Поэтому при извлечении корня степени n из числа z получается n комплексных чисел, все они имеют один модуль и отличаются аргументами. Перебирая значения индекса k от 0 до n-1 в

формуле 2 k , получаем весь набор значений аргумента.

n n

Итак, выражение для корня n-й степени из числа z имеет вид

nz n r cos

n

	2 k					2 k		k 0,1, 2,..., n 1 .
			i sin
	n		n			n

Геометрически n значений корня из числа z представляют собой n вершин правильного n-угольника, как показано на Рис. 4.

Рис. 4

Извлечение корня n-й степени из комплексного числа

Пример. Найдем 4 16 .

Представим -16 в тригонометрической форме: -16=16(cosπ+isinπ).
Для корня 4-й степени получаем четыре значения.
4		4 cos k		i sin k , k 0,1, 2,3.
	16
4			2	4	2

При k=0 При k=1 При k=2 При k=3

w0

w1

w2

w3

4 cos 4 i sin 4 2
	2 2 2i.

3		3	2
					2 2
4 cos 4	i sin 4										2i.
5		5		2
						2 2
4 cos 4		i sin 4										2i.
7		7		2
					2 2
4 cos 4		i sin 4									2i.

Соответствующие векторы показаны на Рис. 5.

Рис. 5 Значения 4 16

m k

2. Элементы линейной алгебры 2.1. Матрицы. Действия над матрицами.

Определение. Матрица – это прямоугольная таблица чисел, в которой каждому элементу однозначно сопоставлены номер строки i и номер столбца j, на пересечении которых он расположен.

Каждый элемент матрицы записывается со своими индексами aij. В общем виде матрица 3 3 имеет вид

	a11	a12	a13
A	a	a	a	.
	21	22	23
	a	a	a
	31	32	33

	1		2	3
Пример матрицы размерности 3 3 : A		4	5	6	.
		7	8	0

Над матрицами определены действия сложение, умножение на число, умножение.

Сложение матриц производится поэлементно.

Известны матрицы A и B, их элементы соответственно обозначены как aij и bij. Пусть C=A+B. Тогда элементы суммы cij находятся по правилу cij=aij+bij.

	1		2	3			1		0	3			2		2	6
Пример.		4	5	6				0	1	0				4	4	6	.
		7	8	0				2	0	7				9	8	7

Умножение матрицы на число – это умножение каждого ее элемента на это число.

B= A определяется как bij= aij

	1		2	3			3		6	9
Пример: 3		4	5	6			12		15	18	.
		7	8	0				21	24	0

Умножение матриц проводится путем последовательного вычисления каждого элемента получающейся матрицы.

На первом шаге анализируются размерности матриц. Операция умножения матриц AB выполнима, только если число столбцов матрицы A равно числу строк матрицы B. В виде формального условия это записывается следующим образом. Если матрица A имеет размерность и матрица B

имеет размерность k n , то можно A умножить на B, при этом размерность результата равна m n .

На втором шаге вычисляется каждый из элементов произведения.

Пусть C=AB. Тогда cij=ai1b1j+ai2b2j+…+aikbkj , где i принимает все возможные значения номеров строк, а j принимает все возможные значения номеров

столбцов матрицы C. В этой сумме каждое слагаемое представляет собой произведение элемента i-й строки первой матрицы на соответствующий элемент j-го столбца второй матрицы; формулу можно запомнить как правило “строка на столбец”.