Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

6.1. Гармонические колебания

Колебаниями называются движения или процессы, которые характеризуются той или иной степенью повторяемости характерной для этого движения или процесса физической величины во времени.

Вфизике различают колебания механические (колебания маятников, струн, частей машин и механизмов, зданий, сооружений и т.п.), электромагнитные (переменный ток в цепи, переменные электромагнитные поля)

иих комбинации. Если значения физических величин повторяются через равные промежутки времени Т, то колебания называются периодическими, а промежуток времени Т называется периодом.

Простейшим и наиболее важным типом периодических колебаний является гармоническое колебание, при котором изменяющиеся во времени физические величины описываются функциями косинуса или синуса.

Система (или материальная точка), совершающая периодическое колебание около положения устойчивого равновесия, называется осциллятором (от латинского слова oscillo – качаюсь). Простейший пример осциллятора в классической механике – груз на пружине.

Взависимости от воздействия, оказываемого на систему, различают

свободные (собственные) колебания, вынужденные колебания, а также па-

раметрические и автоколебания.

Свободными (собственными) называются колебания, которые происходят в отсутствие переменных внешних воздействий. Они могут возникнуть, если систему вывести из состояния равновесия. Например, колебания гитарной струны.

Вынужденными колебаниями называются такие колебания, которые происходят под внешним периодическим воздействием. Примером может служить движение качелей. Человек, раскачивающий качели, представляет собой внешнее периодическое воздействие.

Когда в колеблющейся системе действуют силы сопротивления (например, сила трения) – энергия системы рассеивается. Если потери энергии не восполняются, то колебания со временем прекратятся. В этом случае колебания называются затухающими.

Рассмотрим процесс возникновения колебаний в следующей системе. Шар массой m (рис. 6.1) прикреплен к стене пружиной с жесткостью k и может без трения скользить вдоль горизонтального направления по стержню, продетому сквозь шар. При отклонении шара от положения равновесия у системы увеличивается потенциальная энергия за счет деформации пружины. Если после отклонения систему предоставить самой себе, то сила упругой деформации (рис. 6.1) будет возвращать шар в положение равновесия, при этом потенциальная энергия будет переходить в кинетическую.

94

При приближении к положению равновесия кинетическая энергия (а следовательно и скорость) достигнет максимального значения. Имея ненулевую скорость, шар по инерции пройдет положение равновесия и продолжит двигаться, увеличивая смещение и потенциальную энергию системы. Когда кинетическая энергия шара полностью перейдет в потенциальную энергию деформации, процесс повторится снова, но груз будет двигаться в противоположном направлении. Таким образом, процесс перехода кинетической энергии в потенциальную и обратно будет повторяться беско-

нечно долго.

В реальных колебательных Рис. 6.1 системах всегда присутствуют силы сопротивления, приводящие к потере энергии. Поэтому на практике

свободные колебания являются затухающими. Незатухающие свободные колебания характерны только для идеализированной системы, в которой не действуют силы трения или силы сопротивления среды, как в рассмотренном выше примере.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью периодического внешнего воздействия.

Рассмотрим свободные незатухающие механические колебания более подробно. Введем систему координат так, что ось ОХ будет направлена вдоль стержня, а начало отсчета совпадет с положением равновесия (рис. 6.1).

Систему выведем из равновесия, растянув пружину на малую величину х. Тогда на шар со стороны деформированной пружины будет действовать сила упругости:

F = −kx ,

(6.1)

которая всегда направлена к положению равновесия. Силу с такими свой-

ствами называют возвращающей (или восстанавливающей). В случае дру-

гих колебательных систем возвращающая сила может быть любой по природе, но если для нее выполняется соотношение (6.1), то силу называют

квазиупругой.

Поскольку х – смещение системы от положения равновесия мало, то в разложении потенциальной энергии деформации U(х) в ряд по степеням х можно ограничиться квадратичным членом:

= kx2

U (x) (6.2)

2

95

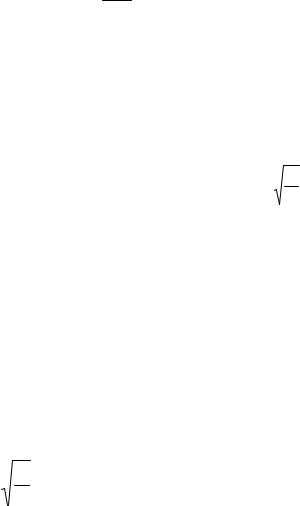
Система, положение которой задается только величиной х, потенциальная энергия имеет вид (6.2), и единственная действующая на систему сила описывается уравнением (VI.1), является типичным линейным гармо-

ническим осциллятором.

Второй закон Ньютона для данной системы примет вид (в проекции на ось OX):

ma = – kx,(VI.3)

= d 2 x

учитывая, что a dt 2 , запишем уравнение в форме

	m		d		2 x		= −kx ,
			dt 2
или
	d 2 x				+		k	x = 0
	dt 2					m
Вводя обозначение
		ω0 =						k ,
получаем								m
	d 2 x				+ω02 x = 0 .
	dt 2

(6.3)

(6.4)

(6.4,а)

(6.5)

(6.6)

Это однородное дифференциальное уравнение второго порядка для

свободных незатухающих колебаний.
Решение уравнения (6.6) имеет вид
x(t)= Acos(ω0t +ϕ0 ),	(6.7,а)
или
x(t)= Asin(ω0t +ϕ0 ),	(6.7,б)

где А –		амплитуда, максимальное смещение от положения равновесия;
ω0 =	k	– собственная круговая частота колебаний; ω0t + ϕ0 – фаза коле-
	m

баний; ϕ0 – начальная фаза.

Из выражения (6.7, а,б) видно, что рассмотренный осциллятор совершает гармонические колебания с собственной круговой частотой ω0.

Теперь определим, как связан период колебаний с собственной круговой частотой. Поскольку в периодическом процессе (в колебаниях) значение физической величины повторяется через период, то для любого момента времени t1 должно выполняться условие

x(t1) = x(t1 +T0 ) .

Так как период функции синуса (и косинуса) равен 2π (рис. 6.2), то можно записать: ω0 (t1 +T0 ) +ϕ0 =ω0t1 +ϕ0 + 2π ,следовательно, после упрощения

96

получим ω0T0 = 2π , или

T0 = 2π

ω0

Рис. 6.2

(6.8)

На (рис. 6.2) показаны графики функции

(6.7, б):

а) зависимость координаты от времени, б) координаты от фазы колебания.

Если за время t система совершает N колебаний, то период определяется выраже – нием

Т = t / N.		(6.9)
Число	колебаний в
единицу	времени	на-
зывается	частотой

колебания и равно

ν = N / t (6.10)

Из выражений (6.9) и (6.10) следует, что период и частота – величины взаимообратные:

	Т= 1/ν .		(6.11)
	Из выражения (6.8) и (6.11) следует
	связь частоты колебаний с собственной
	круговой частотой колебаний
	ω0 = 2πν .		(6.12)
	Рассмотрим основные виды колеба-
	тельных систем.
	Математический маятник		– это
	идеализированная система, состоящая из
	невесомой нерастяжимой нити, закреп-
	ленной на верхнем конце, и материаль-
Рис. 6.3	ной точки массой m, закрепленной на
	нижнем конце нити,	которая может со-
	вершать колебания	около положения

равновесия в поле сил тяжести (или в поле любых других потенциальных сил).

97

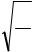
Достаточно хорошим приближением к математическому маятнику является небольшой тяжелый шарик, подвешенный на длинной тонкой нити.

Отклонение от положения равновесия будем характеризовать углом ϕ, образованным нитью с вертикалью (рис. 6.3). При таком выборе направления отсчета угла положительное направление оси вращения ОО’ совпадает с осью Z. Отклонение маятника от равновесия приводит к возникновению момента силы тяжести, его проекция на ось вращения имеет вид

M = −mgl sinϕ ,

(6.13)

где mg – модуль силы тяжести; l sinϕ – плечо этой силы.

Момент силы тяжести М является возвращающим моментом силы, он направлен так, что стремится вернуть маятник в положение равновесия, что и означает знак «минус» в выражении (6.13).

Если силами трения в подвесе маятника и силами сопротивления среды (трением нити и груза о воздух) можно пренебречь, то момент сил тяжести будет единственным моментом сил, действующих на маятник.

Напишем уравнение динамики вращательного движения относитель-

но оси ОО’ (рис. 6.3):
Jε = M ,	(6.14)

где J = ml2 – момент инерции маятника относительно оси ОО’; ε – угловое

ускорение; М – момент силы тяжести относительно той же оси.

Подставляя в формулу (6.14)

выражение для момента (6.13), записы-

вая угловое ускорение в форме

ε =

d 2ϕ

и раскрывая значение момента

dt 2

инерции, получаем

ml 2

d 2ϕ

= −mgl sin ϕ

dt 2

или

d 2ϕ

+

g

sinϕ = 0 .

(6.15)

dt 2

l

При малых отклонениях маятника от положения равновесия можно

принять sin ϕ ≈ ϕ, и уравнение (6.15) привести к виду:

d 2ϕ

+

g

ϕ = 0 .

(6.16)

Вводя обозначения

dt 2

l

ω0 =

g ,

(6.17)

придем к уравнению

d 2ϕ

+ω02ϕ = 0 ,

(6.18)

dt 2

которое аналогично уравнению (6.6) с той лишь разницей, что в последнем случае смещение от положения равновесия характеризуется углом откло-

98

нения нити от вертикали, а не смещением вдоль оси Х, как для груза на пружине.

Решение уравнения (6.18) имеет вид:

ϕ(t)= Acos(ω0t +α0 ), (6.19)

то есть при малых отклонениях от положения равновесия угловое отклонение математического маятника изменяется со временем по гармониче-

скому закону, где: А – амплитуда колебаний; ω0 = g – собственная круго-

вая частота колебаний; α0 – начальная фаза. Из уравнения (VI.8) и (VI.17) получаем, что

T0 = 2π	l .	(6.20)
	g

Как видно из (6.20), период колебаний математического маятника зависит лишь от его длины и ускорения свободного падения, но совершенно не зависит от массы груза. Следовательно, два маятника одинаковой длины, но с разной массой грузов будут колебаться синхронно.

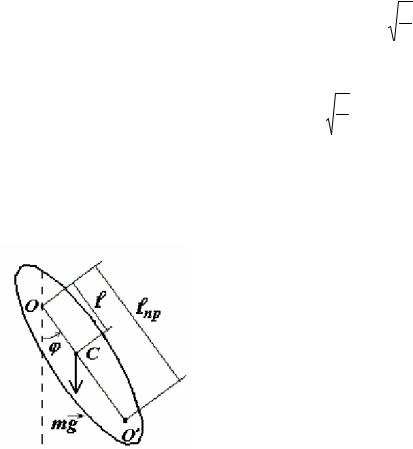
Физическим маятником называется твердое тело, которое может вращаться под действием силы тяжести вокруг неподвижной горизонтальной оси О (рис. 6.4), не проходящей через центр масс С.

Как и в случае математического маятника, при отклонении тела от положения равновесия на угол ϕ возникает возвращающий момент сил тяжести – М, стремящийся вернуть маятник в положение равновесия. Его проекция на ось вращения

Рис. 6.4	M = −mgl sinϕ ,	(6.21)
	где m – масса маятника; – расстояние между

точкой подвеса О и центром масс С маятника. Знак “минус” показывает то, что момент силы тяжести возвращает маятник в положение равновесия.

Уравнение динамики вращательного движения (VI.14) твердого тела вокруг неподвижной горизонтальной оси, проходящей через точку подвеса

О, можно записать в виде:
J	d 2ϕ		= −mgl sinϕ	(6.22)
	dt 2
где J – момент инерции маятника относительно оси О.
При малых углах отклонения sinϕ ≈ϕ выражение (6.22) можно преоб-
разовать к виду:
d 2ϕ		+ mgl ϕ = 0 .		(6.23)
dt 2			J
99

Введя обозначение
	ω0	=	mg ,	(6.24)
получим:			J
	d 2ϕ	+ω02ϕ = 0 .		(6.25)
	dt 2
Видно, что (6.25) аналогично уравнениям (6.6) и (6.12), следовательно,
решение этого уравнения имеет вид
ϕ(t)= Acos(ω0t +α0 ).				(6.26)

Из (6.26) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания. Период этих колебаний равен:

T0 = 2π	J .	(6.27)
	mg

Найдем, какой длины должен быть математический маятник, чтобы период его колебания совпадал с периодом колебаний физического маятника. Из сопоставления формул (6.20) и (6.27) видно, что длина математи-

ческого маятника пр , при которой периоды совпадают, определяется следующим соотношением:

	пр	= J	m	.,T = 2π	lпр	(6.28)
					g
				0

Величину (6.28) называют приведенной длиной физического маятни-

ка. Это длина такого математического маятника, который с данным физическим имеет одинаковый период.

Если пр отложить от точки подвеса по прямой, проходящей через

точку подвеса и центр масс С, то получится точка О′ (см. рис. 6.4), назы-

ваемая центром качания.

Центр качания обладает одним замечательным свойством. Если твердое тело заставить колебаться относительно оси, проходящей через точку

О′, то новые величины приведенной длины ′пр и периода Т′ получатся та-

кими же, как и в случае колебания относительно оси, проходящей через точку О. В этом заключается теорема Гюйгенса. Для ее доказательства будет достаточно найти период колебания маятника относительно оси, проходящей через точку О′, и сравнить его с выражением (6.27) (при этом надо помнить, что расстояние ОО′, равно приведенной длине; моменты инерции для двух случаев будет удобно выразить через момент инерции тела относительно центра масс).

100