
=ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ 1= (1)
.pdf=МАТЕМАТИКА=
О.А. Мокеева
Элементы аналитической геометрии в пространстве
0

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
ВПРОСТРАНСТВЕ
1.Прямоугольная система координат в пространстве
Прямоугольная система координат Oxyz в пространстве оп-
ределяется заданием масштабной единицы измерения длин и трех пересекающихся в одной точке O взаимно перпендикулярных осей: Ox, Oy и Oz . Точка O − начало координат,
Ox − ось абсцисс, Oy − ось ординат, Oz − ось аппликат.
Пусть M − произвольная точка пространства (рис. 1). Проведем через точку M три плоскости, перпендикулярные координатным осям Ox, Oy и Oz . Точки пересечения плоскостей с
осями обозначим соответственно через M x , M y и Mz . |
Прямо- |
||||||
угольными координатами точки M называются числа x |
OM x , |
||||||
|
y OM y , z |
OM z , т. е. величины направленных отрезков |
|||||
|
|
|
|
|
|
|
|
OM x , OM y , |
OM z ; при этом x называется абсциссой, |
y − ор- |
|||||
динатой, а z − аппликатой точки M . Символ M (x; y ; z) обо-
значает, что точка M имеет координаты x, y, z . Если M −
произвольная точка пространства, то вектор OM называется
радиусом-вектором точки M .
Рис. 1 Рис. 2
Таким образом, при выбранной системе координат каждой точке M пространства соответствует единственная упорядоченная тройка чисел (x ; y ; z) − ее прямоугольные координаты и,
1

обратно, каждой упорядоченной тройке чисел (x ; y ; z) соответ-
ствует, и притом одна, точка M в пространстве.
Плоскости Oxy, Oyz, Oxz называются координатными плос-
костями. Они делят все пространство на восемь частей, называемых октантами, которые нумеруют так, как показано на рис. 2.
Расстояние между двумя точками M1(x1; y1; z1) и
M2 (x2 ; y2 ; z2 ) вычисляется по формуле:
d |
|
|
(x |
x )2 |
( y |
y )2 |
|
(z |
2 |
z )2 . |
|
|
(1) |
||||
|
2 |
1 |
2 |
1 |
|
|
1 |
|
|
|
|||||||
Координаты (x; y ; z) точки M , |
делящей в заданном отно- |
||||||||||||||||
шении |
|
|
AM |
|
отрезок |
AB, |
|
(A(x1; y1; z1), B(x2 ; y2 ; z2 )) , |
|||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
MB |
|
|
|||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
определяются по формулам: |
|
|
|
|
|
|
|
|
|||||||||
x |
x1 |
x2 |
, y |
|
y1 |
y2 |
, z |
z1 |
z2 |
. |
(2) |
||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||
В частности, при |
1 |
(точка M делит отрезок |
AB попо- |
||||||||||||||
лам), получаются формулы для определения координат середи-
ны отрезка:
|
|
|
|
|
|
x |
|
|
|
x1 |
x2 |
, y |
|
|
|
y1 |
|
y2 |
|
, z |
|
z1 |
|
|
z2 |
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 1.1. Найти координаты точки А, |
делящей отрезок A1 A2 |
||||||||||||||||||||||||||||||||||||||||||||||
в отношении A1 A : A A2 |
2 : 3 , если A1 (2;4; 1) , |
A2 ( |
3; |
1;6) . |
|
|
|||||||||||||||||||||||||||||||||||||||||
Решение. По условию |
|
|
|
|
|
2 |
|
. По формулам (2) находим: |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
( 3) 2 2 |
|
|
|
|
|
|
|
4 |
|
|
2 |
( 1) 4 |
|
2 |
|
|
10 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
0 , |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
, |
||||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
5 |
|
|
1 |
|
2 |
|
|
|
|
|
5 |
|
|
|
5 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
6 |
1 |
|
4 |
3 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
z |
3 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Точка А имеет координаты |
0;2; |
|
9 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
A |
0;2; |
9 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2

Пример 1.2. Точка C(3;2;4) делит отрезок AB в отношении
53 . Найти координаты точки B, если A( 3;2;1) .
Решение. Пусть B(xB ; yB ; zB ) . Так как точка C делит отрезок
|
AB в отношении |
|
|
3 |
, то по формулам (2): |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
x |
B |
|
|
2 |
3 |
|
y |
B |
|
|
|
|
1 |
3 |
|
z |
B |
|
|
|
|
||||||||||
3 |
|
|
|
|
5 |
|
|
|
, 2 |
|
|
|
5 |
|
|
|
, |
4 |
|
|
|
5 |
|
|
, |
|
|
|
||||||||||||||||||
1 |
3 |
|
|
|
|
|
1 |
|
3 |
|
|
|
1 |
|
3 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
откуда xB 13, |
yB |
|
2 , |
zB |
9 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Ответ: B (13;2;9) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Пример 1.3. На оси Oy |
найти точку, |
равноудаленную от |
|||||||||||||||||||||||||||||||||||||||||||
двух точек A(2;3;1) |
и B ( |
|
1;5; |
2) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Решение. Точка M , |
лежащая на оси Oy , имеет координаты |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BM |
|
|
|
|
|
||||||||||||||||||||||
|
M (0; y;0) . По условию задачи |
AM |
|
|
|
|
. Найдем расстояния |
|||||||||||||||||||||||||||||||||||||||
|
AM |
|
и |
|
BM |
|
, используя формулу (1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
AM |
|
(0 |
|
2)2 |
|
|
( y |
3)2 |
(0 |
|
|
1)2 |
|
|
|
|
y2 |
|
6y |
|
14 , |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
BM |
|
|
(0 |
|
1)2 |
|
( y |
5)2 |
(0 |
|
|
|
2)2 |
|
|
|
|
y2 |
|
10y |
30. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Получим уравнение |
|
|
|
y2 |
|
6y 14 |
|
|
y2 |
|
10y |
30. Отсюда на- |
||||||||||||||||||||||||||||||||||
ходим, что 4 y |
16 , т. е. y |
|
4 . Искомая точка есть M (0;4;0) . |
|||||||||||||||||||||||||||||||||||||||||||
|
Ответ: M (0;4;0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3

2. Плоскость в пространстве
Каждая плоскость в пространстве Oxyz определяется линей-
ным алгебраическим уравнением первой степени. |
|
|||
1. Уравнение |
плоскости, |
проходящей через |
точку |
|
M0 (x0 ; y0 ; z0 ) перпендикулярно вектору n |
( A; B;C) : |
|
||
A(x |
x0 ) B( y y0 ) |
C (z z0 ) |
0. |
(3) |
Ненулевой вектор, перпендикулярный к плоскости, называ-
ется нормальным вектором плоскости.
Вектор n ( A; B;C) − нормальный вектор плоскости (или просто нормаль).
z |
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
M0 |
|
|
|
|
|
O |
|
|
M |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
x |
|
|
|
|
|
||
2. Общее уравнение плоскости: |
|
|
|
|
|||
Ax By Cz D 0 |
|
( A2 |
B2 |
C 2 |
0) . |
||
Частные случаи расположения плоскости: |
|
|
|||||
1) если D 0 , то плоскость Ax |
By |
Cz |
0 проходит через |
||||
начало координат; |
|
|
|
|
|
||
2) если в уравнении плоскости |
Ax |
By |
Cz |
D 0 коэф- |
|||
фициент при какой-то переменной равен нулю, то при D 0
плоскость параллельна соответствующей координатной оси, а
при D 0 плоскость проходит через соответствующую коорди-
натную ось.
4
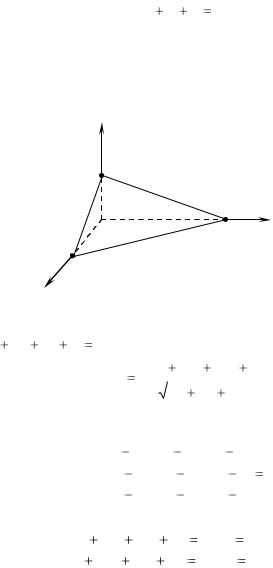
3. Уравнение плоскости в отрезках:
x |
|
y |
|
z |
1, |
|
|
|
|
|
|
a |
|
b |
|
c |
|
|
|
|
где a,b, c − абсцисса, ордината и аппликата точек пересечения плоскостью координатных осей Ox , Oy и Oz соответственно.
Данным уравнением удобно пользоваться при построении плоскости.
z
c |
|
|
O |
b |
у |
a |
|
|
|
|
|
х |
|
|
4. Расстояние d |
от точки M0 (x0 ; y0 ; z0 ) до плоскости |
|
Ax By Cz D 0 находится по формуле:
d |
Ax0 By0 |
Cz0 |
D |
. |
|
|
|
|
|
||
|
A2 B2 |
C 2 |
|
||
|
|
|
|
||
5. Уравнение |
плоскости, проходящей через три данные точ- |
|||||||
ки M1(x1; y1; z1) , |
M2 (x2 ; y2 ; z2 ) , M3 (x3; y3; z3 ) : |
|||||||
|
|
x |
x1 |
y |
y1 |
z |
z1 |
|
|
|
|
||||||
|
|
x2 |
x1 |
y2 |
y1 |
z2 |
z1 |
0 . |
|
|
x3 |
x1 |
y3 |
y1 |
z3 |
z1 |
|
6. Пусть даны две плоскости Q1 и Q2 :
A1x B1 y C1z D1 0 (n1 (A1; B1;C1)) ,
A2 x B2 y C2 z D2 0 (n2 (A2 ; B2 ;C2 )) .
5
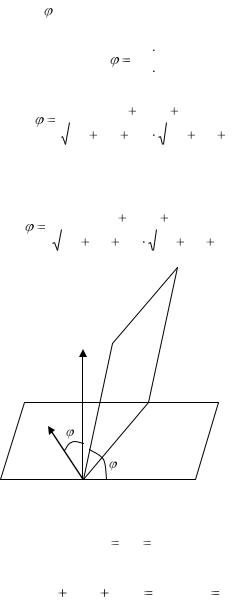
В качестве угла между плоскостями Q1 |
и Q2 принимают |
|||||||||||||||||||||
угол между их нормальными векторами: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
cos |
|
|
n1 |
n2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n1 |
|
|
n2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
или в координатной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cos |
|
|
|
A1 A2 |
|
B1B2 C1C2 |
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
A2 |
B2 |
|
C 2 |
|
|
A2 |
B2 |
C 2 |
|||||||||
1 |
1 |
|
1 |
|
2 |
2 |
2 |
|
|
|||||||||||||
Для нахождения острого угла: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cos |
|
|
|
|
|
A1 A2 |
|
B1B2 |
|
|
C1C2 |
|
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A2 |
B2 |
C2 |
|
A2 |
B2 |
C2 |
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
1 |
1 |
|
1 |
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
||||||
Q2
n1
Q1
n2
Условие параллельности двух плоскостей:
A1 |
|
B1 |
|
C1 |
. |
|
|
|
|
||
A2 |
|
B2 |
|
C2 |
|
Условие перпендикулярности двух плоскостей:
A1A2 B1B2 C1C2 0 (n1  n2 0) .
n2 0) .
6
Плоскости совпадают, когда
|
A1 |
|
B1 |
|
C1 |
|
D1 |
. |
|
|
|
|
|
|
|
||
|
A2 |
|
B2 |
C2 |
|
D2 |
||
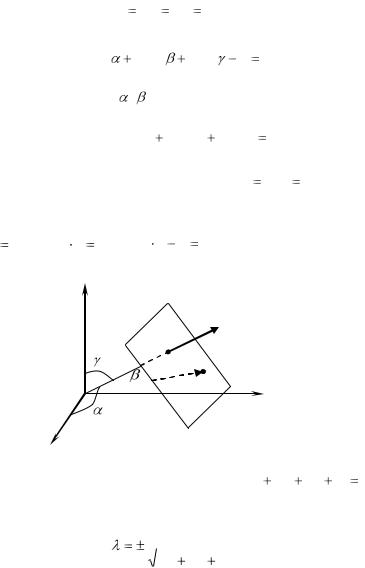
7. Нормальное уравнение плоскости: |
||||||||
x cos |
y cos |
|
z cos p 0 , |
|||||
где p − длина перпендикуляра OK , опущенного из начала координат на плоскость; , ,  − углы, образованные единичным вектором e , имеющего направление перпендикуляра OK ,
− углы, образованные единичным вектором e , имеющего направление перпендикуляра OK ,
с осями Ox , Oy и Oz (cos 2 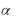 cos 2
cos 2 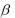 cos 2
cos 2  1) .
1) .
Возьмем на плоскости произвольную точку M (x; y ; z) и соеди-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ним ее с началом координат. Образуем вектор |
|
|
ОМ (x ; y ; z) . |
||||||||||||
r |
|||||||||||||||
При любом положении точки M на плоскости Q проекция |
|||||||||||||||
радиус-вектора |
|
|
|
на направление вектора e |
всегда равна p : |
||||||||||
r |
|||||||||||||||
прe |
|
p , т. е. |
|
|
e |
p или |
|
e |
p 0 . |
|
|
||||
r |
r |
|
r |
|
|
||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
p K |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
M |
|
|
|||
|
|
|
|
|
|
|
|
r |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
O 
Q y
x
Замечание. Общее уравнение плоскости Ax By Cz D 0
приводится к нормальному виду путем умножения на норми-
рующий множитель
|
1 |
|
, |
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
||
|
|
|
учитывая, что знак перед дробью берется противоположным знаку свободного члена D общего уравнения плоскости.
7
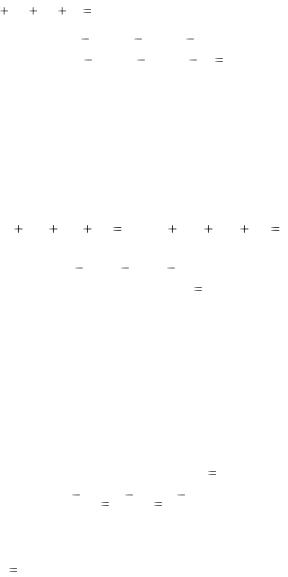
8. Плоскость P , проходящая через две точки M1(x1; y1; z1) и M2 (x2 ; y2 ; z2 ) перпендикулярно к плоскости Q, заданной урав-
нением Ax By Cz D |
0 , представляется уравнением |
|
||||||
|
x |
x1 |
y |
y1 |
z |
z1 |
|
|
|
|
|
||||||
|
x2 |
x1 |
y2 |
y1 |
z2 |
z1 |
0 . |
(4) |
|
|
A |
|
B |
|
C |
|
|
Замечание. В случае, когда прямая M1M2 |
перпендикулярна к |
|||||||
плоскости Q, плоскость P неопределенна. В соответствии с этим уравнение обращается в тождество.
9. Плоскость P, проходящая через точку M1(x1; y1; z1) и
перпендикулярная к двум (непараллельным) плоскостям Q1 , |
Q2 : |
||||||
A1x B1 y C1z D1 |
0 , A2 x B2 y C2 z D2 |
0 , |
|
||||
представляется уравнением |
|
|
|
|
|
|
|
|
x x1 |
y y1 |
z z1 |
|
|
|
|
|
|
|
|
|
|||
|
A1 |
B1 |
C1 |
|
0 . |
|
(5) |
|
A2 |
B2 |
C2 |
|
|
|
|
Замечание. В случае параллельности |
плоскостей |
Q1 , |
Q2 |
||||
плоскость P неопределенна. В соответствии с этим уравнение обращается в тождество.
3.Прямая в пространстве
1.Канонические уравнения прямой, проходящей через данную
точку M0 (x0; y0; z0 ) параллельно вектору s (m; n; p) :
x x0 |
|
y y0 |
|
z z0 |
. |
|
|
|
|
||
m |
|
n |
|
p |
|
Всякий ненулевой вектор, параллельный данной прямой, на-
зывается направляющим вектором этой прямой.
Вектор s (m; n; p) − направляющий для прямой.
8

2. Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей.
Общие уравнения прямой:
A1x B1 y C1z D1 0, A2 x B2 y C2 z D2 0
(коэффициенты при переменных не пропорциональны).
Направляющий вектор данной прямой находится по формуле:
|
|
|
B1 |
C1 |
; |
A1 |
C1 |
; |
A1 |
B1 |
. |
|
s |
(6) |
|||||||||||
|
|
|
B2 |
C2 |
|
A2 |
C2 |
|
A2 |
B2 |
|
|
3. Необходимое и достаточное условие расположения двух прямых в одной плоскости (условие компланарности двух прямых):
x2 x1 |
y2 |
y1 z2 |
z1 |
|
|
m1 |
n1 |
p1 |
|
0 . |
(7) |
m2 |
n2 |
p2 |
|
|
|
Замечания.
1)если в определителе все строки пропорциональны, то пря-
мые совпадают;
2)если пропорциональны только вторая и третья строки, то
прямые параллельны;
3)если определитель равен нулю, но вторая и третья строки непропорциональны, то прямые пересекаются;
4)если определитель не равен нулю, то прямые скрещиваются.
4. Расстояние от точки M0 (x0 ; y0 ; z0 ) до прямой
x x1 |
|
|
y y1 |
|
|
|
z z1 |
вычисляется по формуле: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
m1 |
|
|
n1 |
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
y |
y |
0 |
z z |
0 |
|
2 |
|
x x |
z z |
0 |
|
2 |
|
x x |
y |
y |
0 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
0 |
1 |
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|||||
d |
|
|
n1 |
|
|
p1 |
|
|
|
|
|
m1 |
|
p1 |
|
|
|
|
|
m1 |
|
|
n1 |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
n2 |
p2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9
