26.4. Рассмотрение K-множеств
Для ускорения процесса противогоночного кодирования состояний асинхронного автомата вместо рассмотрения пар переходов можно рассматривать пары так называемых K-множеств.
K-множеством называется множество состояний асинхронного автомата, переходы из которых при некотором фиксированном входном сигнале ведут в одно и то же состояние (также принадлежащее данному множеству). Пусть таблицу переходов автомата представляет табл. 26.4. K-множествами при входном сигнале а1 являются {q1, q3}, {q2, q4, q5} и {q6, q7}.
Таблица 26.4 Таблица переходов асинхронного автомата
q1 |
а1 |
а2 |
а3 |
а4 |
а5 |
q1 |
q5 |
q1 |
q5 |
q2 |
|
q2 |
q2 |
q6 |
q2 |
– |
q2 |
q3 |
q1 |
– |
q4 |
q3 |
– |
q4 |
q2 |
q5 |
q4 |
– |
q6 |
q5 |
q2 |
q5 |
q1 |
q5 |
– |
q6 |
q7 |
q6 |
q2 |
q3 |
q6 |
q7 |
q7 |
q5 |
– |
q3 |
q6 |
Парой K-множеств в дальнейшем будем называть два различных K-множества, построенных для одного и того же входного сигнала. Так же, как для пары переходов, для каждой пары K-множеств строится троичный вектор, компоненты которого соответствуют состояниям автомата. Компоненты, соответствующие состояниям, которые принадлежат одному из этих K- множеств, имеют значение 0; компоненты, соответствующие состояниям из другого K-множества, – значение 1, а компоненты, соответствующие состояниям, не принадлежащим ни одному их этих K-множеств, – значение «–». Множество построенных таким образом векторов для всех пар K-множеств, из которого удалены имплицируемые векторы, образует матрицу условий S*, имплицирующую матрицу S.
Действительно, каждой из строк матрицы S, полученной при рассмотрении пары переходов qi → qj, qk → ql, соответствует некоторая строка матрицы S*, полученная при рассмотрении пары K-множеств, одному из которых принадлежат состояния qi и qj, а другому – состояния qk и ql. При этом строка матрицы S* имплицирует строку матрицы S. Благодаря транзитивности отношения импликации кратчайшая имплицирующая форма матрицы S* имплицирует также и матрицу S.
Процесс получения кратчайшей имплицирующей формы матрицы S* ничем не отличается от описанного ранее процесса получения кратчайшей имплицирующей формы матрицы S, т. е. так же строятся максимальные
185
совместимые множества строк и отыскивается кратчайшее покрытие строк матрицы S* этими множествами.
В общем случае матрица S* неэквивалентна матрице S, т. е. не всегда матрица S имплицирует S*. Поэтому для одного и того же автомата кратчайшая имплицирующая форма матрицы S* может иметь большее число строк, чем кратчайшая имплицирующая форма матрицы S. Однако рассмотрение пар K- множеств менее трудоемко по сравнению с рассмотрением пар переходов.
Проиллюстрируем данный метод кодирования на примере табл. 26.4. Здесь нет необходимости вводить дополнительный столбец, как это сделано в предыдущем примере, поскольку нет одинаковых строк. Для данного автомата получаем матрицу условий
q1 |
q2 |
q3 |
q4 |
q5 q6 q7 |
|
||||
|
0 |
1 |
0 |
1 |
1 |
− |
− |
1 |
|
0 |
− |
0 |
− |
− |
1 |
1 |
|
2 |
|
|
|
0 |
− |
0 |
0 |
1 |
1 |
|
3 |
− |
|
||||||||
S* = |
0 |
1 − 0 |
0 |
1 |
0 |
|
4 . |
||
0 |
− |
1 |
1 |
0 |
− |
− |
5 |
||
− |
0 |
1 |
1 |
− |
0 |
− |
6 |
||
|
0 |
− |
1 |
− |
0 |
1 |
1 |
|
7 |
|
|
||||||||
|
0 |
0 |
− |
1 |
− |
1 |
1 |
|
8 |
|
|
|
|
|
|
|
|
|
|
Для троичной матрицы S* получим следующие максимальные совместимые множества и соответствующие им векторы:
{1, 2} (0 1 0 1 1 1 1); {1, 3} (0 1 0 1 1 0 0); {2, 3} (0 0 0 0 0 1 1); {2, 6} (0 1 0 0 – 1 1); {2, 8} (0 0 0 1 – 1 1); {3, 7} (0 0 1 0 0 1 1), {4, 6} (0 1 0 0 0 1 0); {5, 6} (0 0 1 1 0 0 –); {5, 7, 8} (0 0 1 1 0 1 1).
Совокупность множеств {1, 2}, {1, 3}, {4, 6} и {5, 7, 8} является кратчайшим покрытием множества строк матрицы S*. Матрица кодирования для рассматриваемого автомата имеет вид
186
|
z1 |
z2 |
z3 |
z4 |
q |
|
0 |
0 |
0 |
0 |
|
|
1 |
1 |
1 |
0 |
q12 |
C = |
0 |
0 |
0 |
1 |
q |
1 1 |
0 |
1 |
q3 . |
||
|
|
|
|
|
4 |
|
1 |
1 |
0 |
0 |
q5 |
|
|
0 |
1 |
|
q6 |
|
1 |
1 |
|||
|
1 |
0 |
0 |
1 |
q7 |
Функции возбуждения строятся на интервалах, каждый из которых соответствует K-множеству. Для этого представим входной сигнал многозначной переменной а, принимающей значения а1, а2, а3, а4, а5, и получим следующие матрицы:
a z1 z2 |
z3 z4 |
|
|
z + |
z |
+ |
z |
+ |
z |
|
+ |
||||
a1 0 0 |
0 |
− |
|
|
1 |
|
2 |
|
3 |
|
4 |
||||
|
|
0 0 |
|
0 |
0 |
||||||||||
a1 1 1 |
− − |
|
|
1 1 |
1 |
0 |
|||||||||
|
|
1 0 |
− |
1 |
|
|
|
1 0 |
|
0 |
1 |
||||
a1 |
|
|
|
|
|||||||||||
a2 − − |
0 |
− |
|
|
1 1 |
|
0 |
0 |
|||||||
a |
|
1 − |
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
1 |
1 |
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
||||||
U = a3 − − |
0 |
0 |
|
, |
V = |
0 0 |
|
0 |
0 . |
||||||
|
|
1 − |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
a3 |
− |
|
|
1 1 |
0 |
||||||||||
a3 − − |
0 |
1 |
|
|
1 1 |
|
0 |
1 |
|||||||
a4 − − |
0 |
0 |
|
|
|
1 1 |
|
0 |
0 |
||||||
|
|
− 0 |
− |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
a4 |
|
|
|
0 0 |
|
1 |
|||||||||
a5 − − |
− 0 |
|
|
|
1 1 |
1 |
0 |
||||||||
|
|
1 − |
− |
1 |
|
|
|
1 0 |
1 |
1 |
|||||
a5 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученные функции можно упростить за счет расширения интервалов:
a z1 z2 |
z3 z4 |
|
|
z + |
z |
+ |
z |
+ |
z |
|
+ |
||||
a1 0 0 |
− − |
|
|
1 |
|
2 |
|
3 |
|
4 |
|||||
|
|
0 0 |
|
0 |
0 |
||||||||||
a1 − 1 |
− − |
|
|
1 1 |
1 |
0 |
|||||||||
|
|
1 0 |
|
|
|
|
|
1 0 |
|
0 |
1 |
||||
a1 |
− − |
|
|
|
|||||||||||
a2 − − |
0 |
− |
|
|
1 1 |
|
0 |
0 |
|||||||
a |
|
− − |
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
1 |
1 |
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
||||||
U = a3 − − |
0 |
0 |
|
, |
V = |
0 0 |
|
0 |
0 . |
||||||
|
|
− − |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
a3 |
− |
|
|
1 1 |
0 |
||||||||||
a3 − − |
0 |
1 |
|
|
1 1 |
|
0 |
1 |
|||||||
a4 − − |
− 0 |
|
|
|
1 1 |
|
0 |
0 |
|||||||
|
|
− − |
− |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
a4 |
|
|
|
0 0 |
|
1 |
|||||||||
a5 − − |
− 0 |
|
|
|
1 1 |
1 |
0 |
||||||||
|
|
− − |
− |
1 |
|
|
|
1 0 |
1 |
1 |
|||||
a5 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
187
26.5. Соседнее кодирование состояний
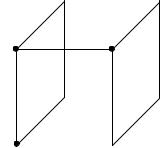
До сих пор рассматривались прямые переходы, когда элементы памяти одновременно меняют свои состояния. Можно избавиться от опасных состязаний, устранив вообще состязания между элементами памяти. Каждый из прямых переходов можно заменить последовательностью элементарных переходов, т. е. таких, в которых меняется состояние только одного элемента памяти. В этом случае удобно представить коды состояний как элементы булева пространства внутренних переменных, а переход из состояния в состояние – как движение по ребрам полного булева графа, или гиперкуба, из вершины в вершину. Упомянутая последовательность элементарных переходов представится тогда последовательностью пройденных ребер.
Кодирование состояний сводится к размещению состояний на вершинах гиперкуба. Можно использовать также процесс сборки гиперкуба, применяемый при кодировании синхронного автомата методом «желательных соседств». Рассмотрим использование этого процесса для соседнего кодирования состояний асинхронного автомата.
В данном случае также вводится величина wij, задаваемая на парах состояний автомата, только теперь она представляет коэффициент связи – число K-множеств, содержащих пару состояний qi, qj. Дальнейшая сборка гиперкуба ничем не отличается от той, которая применяется при кодировании состояний синхронного автомата. Заметим только, что при подсчете значения wij одно и то же K-множество учитывается столько раз, сколько раз оно определяется различными входными сигналами.
После того как гиперкуб собран, в нем выделяются подграфы, порожденные K-множествами. Эти подграфы должны быть связными, и на них накладывается следующее ограничение. Подграфы, которые соответствуют K- множествам, определяемым одним и тем же входным сигналом, не должны пересекаться.
В K-множестве устойчивым является только одно состояние. В подграфе, соответствующем K-множеству, можно сориентировать ребра согласно переходам, заканчивающимся всегда в устойчивом состоянии. Состояния, связанные элементарным переходом, располагаются на соседних вершинах. Если не удается выделить связные подграфы в гиперкубе, непересекающиеся и соответствующие K-множествам, которые определяются одним и тем же входным сигналом, надо увеличить размерность гиперкуба на единицу и проложить цепочку элементарных переходов, по крайней мере, для одного прямого перехода через другой подкуб.
Обозначим K-множество, определяемое входным сигналом ai и устойчивым состоянием qj, символом Kij и рассмотрим автомат, заданный табл. 26.4. Для него получим все K-множества:
188
K11 = {q1, q3}, K12 = {q2, q4, q5}, K17 = {q6, q7};
K25 = {q1, q4, q5, q7}, K26 = {q2, q6};
K31 = {q1, q5}, K32 = {q2, q6}, K34 = {q3, q4};
K43 = {q3, q6, q7}, K45 = {q1, q5};
K52 = {q1, q2}, K56 = {q4, q6, q7}.
Значения wij представим с помощью табл. 26.5. Результат процесса сборки гиперкуба показан на рис. 26.1.
Таблица 26.5
|
|
|
|
Значения wij |
|
|||
q2 q3 q4 q5 q6 q7 q8 |
q1 |
|||||||
1 |
1 |
1 |
3 |
|
0 |
1 |
0 |
|
|
0 |
1 |
1 |
|
2 |
0 |
0 |
q2 |
|
|
1 |
0 |
|
1 |
1 |
0 |
q3 |
|
|
|
2 |
|
1 |
2 |
0 |
q4 |
|
|
|
|
|
0 |
1 |
0 |
q5 |
|
|
|
|
|
|
3 |
0 |
q6 |
|
|
|
|
|
|
|
0 |
q7 |
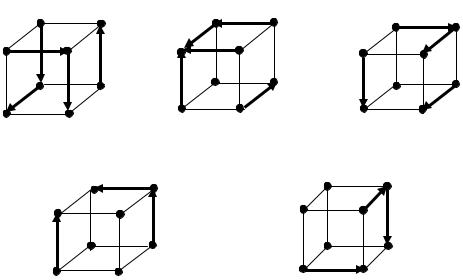
Разместим теперь в этом гиперкубе связные подграфы, соответствующие K-множествам, и снабдим ребра этих подграфов ориентацией, соответствующей направлениям переходов (рис. 26.2). В данном примере удалось без увеличения размерности гиперкуба разместить их так, чтобы любые два из них, соответствующие одному и тому же входному сигналу, не пересекались.
q3 
q7
q5 |
q4 |
q8 
q6
q1
q2
Рис. 26.1. Гиперкуб, представляющий соседство состояний
189
|
q3 |
q7 |
q3 |
q7 |
|
q3 |
q7 |
q5 |
q4 |
q5 |
q4 |
|
q5 |
q4 |
|
|
q8 |
q6 |
q8 |
q6 |
|
q8 |
q6 |
q1 |
q2 |
q1 |
q2 |
|
q1 |
q2 |
|
|
a1 |
|
a2 |
|
|
a3 |
|
|
q3 |
q7 |
|
|
q3 |
q7 |
|
|
q5 |
q4 |
|
q5 |
q4 |
|
|
|
q8 |
q6 |
|
|
q8 |
q6 |
|
|
q1 |
q2 |
|
q1 |
|
q2 |
|
|
a4 |
|
|
a5 |
|
|
|
|
|
Рис. 26.2. Цепочки элементарных переходов |
|
||||
Преобразуем теперь исходную таблицу в таблицу элементарных переходов, которая представлена в виде табл. 26.6.
Таблица 26.6 Таблица элементарных переходов
q1 |
а1 |
а2 |
а3 |
а4 |
а5 |
q1 |
q5 |
q1 |
q5 |
q2 |
|
q2 |
q2 |
q6 |
q2 |
– |
q2 |
q3 |
q8 |
q5 |
q7 |
q3 |
– |
q4 |
q2 |
q5 |
q4 |
– |
q7 |
q5 |
q4 |
q5 |
q1 |
q5 |
– |
q6 |
q7 |
q6 |
q2 |
q7 |
q6 |
q7 |
q7 |
q3 |
q4 |
q3 |
q6 |
q8 |
q1 |
– |
– |
– |
– |
Функции возбуждения элементов памяти строятся здесь так же, как для синхронного автомата.
190