Текст задания:

Пример 1.

Даны векторы  a(2;1) и b(-1;1). Каковы координаты вектора a + b?

Пример 2.Даны векторы a(2;1) и b(-1;2). Каковы координаты вектора a - b?

Пример 3.Даны векторы a(2;1) и b(-1;1). Каковы координаты вектора 0,5a - 2b?

Пример 4.Упростить выражение:

.

Пример 5. Даны векторы . Коллинеарны ли эти векторы? Пример 6. Найти длину вектораx= (3; 0; 4).

Пример 7. Даны точки:

Выяснить, равнобедренный ли треугольник, построенный на этих точках.

Пример 8.Даны два вектора:

.

Найти .

Пример 9.Даны четыре вектора:

, ,,.

Найти координаты векторов и.

Пример 10. Даны. Найти, если

Пример 11. Доказать, что вектор 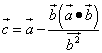ортогонален (перпендикулярен) вектору 

Пример 12. Даны длины двух векторов и угол между ними:

.

Определить, при каком значении векторыиортогональны (перпендикулярны).

Пример 13. Даны векторы:

.

Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?

Пример 14. Даны три точкиA(1;1;1),B(2;2;1),C(2;1;2).

Найти угол .

Пример 15. Даны два вектора

и

Найти сумму, разность, длину, скалярное произведение и угол между ними.

Пример 16. Среди векторов

Найти а) коллинеарные; б) ортогональные.

Контрольные вопросы:

[2, стр. 286(18 – 20)]

Элементы комбинаторики, статистики и теории вероятностей

уметь:

- Решать простейшие комбинаторные задачи методом перебора, а так же с использованием известных формул;

- Вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

- Анализа реальных числовых данных, представленных в виде диаграмм, графиков;

- Анализа информации статистического характера;

Раздел 9. Элементы теории вероятностей. Элементы математической статистики

Самостоятельная работа № 21

Тема: Решение комбинаторных задач

Цель: закрепить знания и умения студентов по освоению темы методом решения задач.

Теоритическое обоснование:

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n_i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n₁*n₂*n₃*...*n_k.

Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n₁ элементов, а вторая - из n₂ элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n₂. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n₂. Так как в первой группе всего n₁ элемент, всего возможных вариантов будет n₁*n₂.

Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?

Решение: n₁=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n₂=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6). Итак, N=n₁*n₂*n₃=6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n₁=n₂=...n_k=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n^k. Такой способ выбора в комбинаторики носит название выборки с возвращением.

Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8? Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5⁴=625. Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью.

Число размещений из n элементов по m