ОиАСУ / Лабораторная работа 2

ЛАБОРАТОРНАЯ РАБОТА №2 РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Цель работы: получение навыков по решению дифференциальных уравнений различными методами в среде Mathcad

Порядок выполнения работы

Для заданных дифференциальных уравнений найти решения при различных начальных условиях и различных правых частях методами:

• преобразований Лапласа;

• Эйлера (численно с переходом к уравнениям в конечных разностях);

• одним из численных методов, реализованным в виде процедуры Mathcad, например, с помощью блока Given и функции odesolve(t,Тк[n]).

Если выбранный метод не позволяет получить решение, перейти к следующему методу или следующей задаче.

Теоретические сведения

1. Решение с помощью обратного преобразования Лапласа

Последовательность решения:

• Записать дифференциальное уравнение в преобразованиях Лапласа с учетом начальных условий. Для этого необходимо выполнить преобразование Лапласа отдельно для левой и правой частей уравнения, например, уравнение

= k sin(t)

в преобразованиях Лапласа будет иметь вид:

TsY(s) - Ty(0) + Y(s)=k/();

• Выразить в явном виде Y(s) из полученного выражения:

• Выполнить обратное преобразование Лапласа, используя необходимые упрощающие условные обозначения, например, y(0)=y0; если функция-изображение громоздкая, обратное преобразование можно выполнять по частям для отдельных слагаемых или групп слагаемых. Результат обратного преобразования Лапласа – искомая функция y(t).

• Для построения графика функции необходимо задать значения параметров уравнения и упростить полученное выражение:

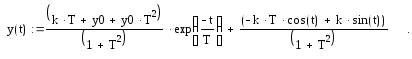
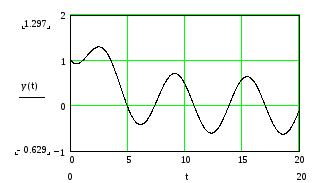Рис. 2.1. График решения

2. Приближенное численное решение

Последовательность решения:

• заменить производные в дифференциальном уравнении отношением конечных разностей:

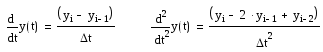
• из полученного уравнения выразить функцию с максимальным индексом через остальные составляющие, задать значения переменным и интервал изменения индекса (количество определяемых точек):

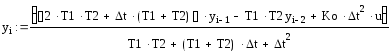
• построить график:

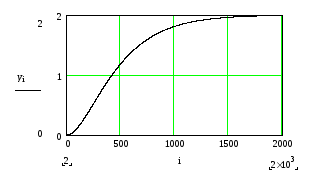
Рис. 2.2. График решения

3. Решение с помощью блока Given и функции odesolve

Последовательность решения:

• записать все исходные параметры, за исключением начальных условий

• указать начало блока Given

• записать дифференциальное уравнение и начальные условия, причем, знак равенство используется из логических операций, знак дифференцирования для начальных условий – в левом верхнем углу клавиатуры:

• записать функцию odesolve в виде

z:= odesolve(t, p,[n]),

где t – переменная интегрирования,

p – верхний предел изменения t (нижний равен 0),

n – число точек, определяющее шаг приближенного интегрирования (n = p/t). Если число точек не задано – шаг выбирается автоматически из условия допустимой погрешности.

п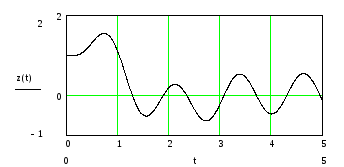 остроить график функции:

Рис. 2.3. График решения

Примеры выполнения

Решение дифференциального уравнения с помощью преобразований Лапласа

_{Решим уравнение:}

Выполним преобразования Лапласа отдельно для левой и правой частей уравнения. Выписываем левую часть уравнения:

Отмечаем переменную t и выбираем пункт меню Символы –> Преобразования –>Лапласа. Результат размещается под исходной строкой. Правая часть уравнения в преобразованиях Лапласа имеет вид:

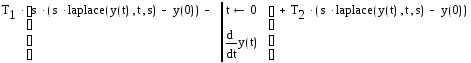
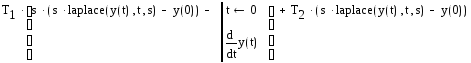
Выполним преобразования Лапласа для левой части уравнения с использованием функции laplace

Уравнение в преобразованиях Лапласа имеет вид:

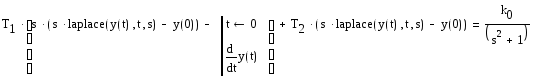
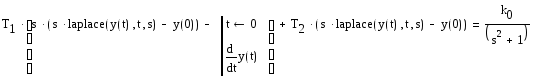
В последнем выражении laplace(y(t),t,s) – обозначение на входном языке MathCad Y(s). Для простоты дальнейших преобразований будем считать, что Y(s)=Y, Y(0)=Y₀, Y' (0)=Y₁₀. Введем замену:

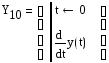
После чего исходное уравнение в преобразованиях Лапласа имеет вид:

Выражаем отсюда Y, (отмечаем переменную Y курсором и выбираем пункт меню Символы - Переменные - Вычислить):

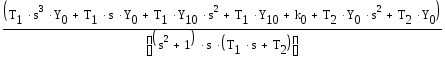
Для простоты примем начальные условия нулевыми, тогда Y в преобразованиях Лапласа имеет вид:

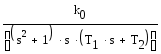
Выполняем обратные преобразования Лапласа от полученного выражения и присваиваем полученный результат функции y(t). Задаем значения коэффициентов и строим график функции.

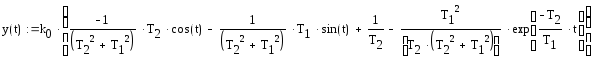
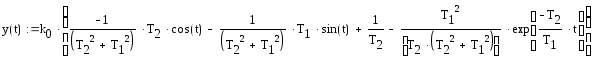
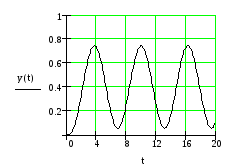
Рис. 2.4. График решения

Решение дифференциального уравнения методом Эйлера

_{Решим уравнение:}

Записываем уравнение в конечных разностях (y_i - индексированная переменная) с учетом конечно-разностных выражений для первой и второй производных выведенных выше:

Выражаем y_i, задаем значения коэффициентов и нулевые начальные условия:

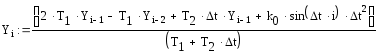
Строим графики функций Yi, полученной методом конечных разностей, и y(t), полученной с помощью преобразований Лапласа:

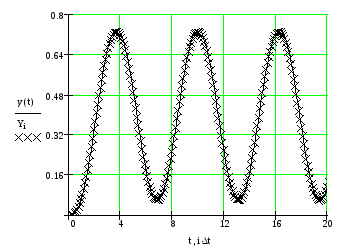
Рис. 2.5. Графики решений

Решение дифференциального уравнения с помощью функции odesolve

Решим уравнение

Задаем значения коэффициентов :

_{Записываем блок решения уравнения по правилам, изложенным выше.}

Строим графики функций Y_odes, полученной с помощью функции odesolve, и y(t), полученной с помощью преобразований Лапласа:

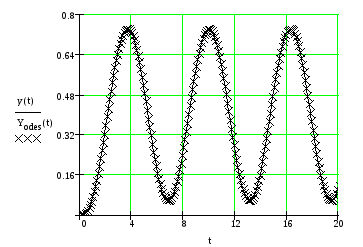
Рис. 2.6. Графики решений

Графические изображения решений уравнения, полученных тремя различными способами, полностью совпадают.

Контрольные вопросы

1. Как записать аналитическое решение неоднородного уравнения первого порядка для различных правых частей?

2. Как записать аналитическое решение неоднородного уравнения второго порядка для различных правых частей и при различных типах корней характеристического уравнения?

3. Как получить решение дифференциального уравнения с помощью преобразований Лапласа (на примере конкретного уравнения)?

4. Как получить приближенное решение дифференциального уравнения второго порядка одним из численных методов?

Содержание отчета

1. Титульный лист.

2. Название и цель работы.

3. Постановку задачи в соответствии с вариантом задания.

4. Решения дифференциальных уравнений, полученные тремя способами и графики решения.

5. Выводы.

Задания

Решить уравнение, выданное преподавателем, с помощью преобразований Лапласа, методом Эйлера и с использованием функции odesolve.

1.

2.

3.

4.

В соответствии со своим вариантом правую часть уравнения – F(t) – взять из табл. 1.1, коэффициенты уравнения – из табл. 1.2.

Таблица 2.1.

Вариант	F(t)	Вариант	F(t)	Вариант	F(t)
1	sin(2t)	9	2t^2-3t	17	0,9 exp(3t)
2	cos(5t)	10	2 cos(t)-sin(t)	18	0,15 t^2
3	exp(-2t)	11	4,9 t-2	19	4 exp(t)
4	2t^2-3	12	1,2 exp(-2t)	20	3cos(2,5t)
5	8,5 - t	13	3,8 sin(0,2 t)	21	6 exp(-2t)
6	3,8t	14	4,2 cos(3t)	22	4,3 t-5
7	4 cos(0,2t)	15	0,8 t-2	23	0,8 sin(2t)
8	2exp(-5,6t)	16	3,9 t^2-2t	24	4,9 t^2

Таблица 2.2.

Вариант	T1	T2	k	Вариант	T1	T2	k
1	0,5	0,8	1,2	13	0,56	0,98	1,4
2	1,18	5,94	0,87	14	0,14	2,37	1,67
3	0,14	0,12	0,01	15	8,63	4,9	0,87
4	11	5	3	16	7,9	0,45	4,68
5	0,85	0,68	0,23	17	1,54	0,82	2,38
6	4,23	4,87	3,56	18	2,18	7,54	0,9
7	0,15	0,18	1,67	19	0,43	0,59	1,24
8	0,58	0,97	0,45	20	3,1	2,47	6,71
9	5,74	5,61	3,28	21	1,86	0,79	1,14
10	0,45	0,78	0,25	22	1,37	2,145	2,56
11	1,42	1,78	2,64	23	3,71	1,15	4,57
12	0,84	1,27	0,47	24	2,43	3,47	5,11