
- •В.А. Павский линейная алгебра
- •Оглавление
- •Введение
- •I. Введение в линейную алгебру § 1. История развития алгебры
- •§ 2. Множества
- •§ 3. Строение множеств
- •Алгебра множеств
- •§ 4. Число Развитие
- •§ 5. Числовые множества
- •Бесконечные множества
- •Натуральный ряд
- •Множество целых чисел
- •Множество рациональных чисел
- •Множество действительных чисел
- •Множество комплексных чисел
- •Суммы и произведения
- •Приближенные вычисления
- •II. Элементы линейной алгебры § 1. Матрицы и определители 3, 7
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •Определитель матрицы
- •Свойства определителей
- •Вычисление определителей
- •Аксиоматическое построение теории определителей
- •Обратная матрица
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •§ 2. Системы линейных алгебраических уравнений
- •Методы решения слау
- •1. Метод Крамера
- •2. Матричный метод
- •3. Метод Гаусса
- •Однородная система линейных алгебраических уравнений (ослау)
- •§ 3. Системы линейных алгебраических неравенств
- •III. Линейные пространства
- •§ 1. Линейная зависимость
- •§ 2. Линейные комбинации. Базисы
- •§ 3. Подпространства
- •§ 4. Прямые суммы
- •§ 5. Евклидовы пространства
- •§ 6. Координатные системы
- •IV. Векторная алгебра § 1. Векторы
- •§ 2. Линейные операции над векторами
- •§ 3. Проекция вектора на ось
- •Линейные свойства проекции вектора на ось
- •Координаты вектора
- •Деление отрезка в данном отношении
- •§ 4. Базис системы векторов
- •§ 5. Скалярное произведение векторов
- •§ 6. Векторное произведение векторов 4
- •Геометрические свойства векторного произведения
- •Алгебраические свойства векторного произведения
- •§ 7. Смешанное произведение векторов 4
- •V. Аналитическая геометрия 4
- •§ 1. Системы координат на плоскости
- •§ 2. Уравнение линии на плоскости
- •§ 3. Уравнение поверхности и линии в пространстве
- •§ 4. Прямая и плоскость в линейном пространстве
- •Уравнение плоскости, проходящей через три точки
- •Взаимное расположение плоскостей
- •Уравнение прямой в пространстве r3
- •Уравнение прямой, проходящей через две точки
- •Прямая как линия пересечения плоскостей
- •Расстояние от точки до прямой
- •Угол между прямой и плоскостью
- •Угол между плоскостями
- •VI. Линейные операторы § 1. Линейный оператор
- •Векторные свойства линейных операторов
- •Умножение операторов
- •Матрицы операторов
- •Изменение базиса 3, 11
- •Подобие 11
- •§ 2. Характеристический многочлен
- •VII. Билинейные и квадратичные формы § 1. Билинейные формы
- •§ 2. Квадратичные формы
- •Приведение к каноническому виду
- •VIII. Гиперповерхности и поверхности второго порядка
- •Классификация линий второго порядка
- •Окружность
- •Гипербола
- •Парабола
- •Классификация поверхностей второго порядка
- •Заключение
- •Список литературы
- •Линейная алгебра
- •650002, Г. Кемерово, ул. Институтская, 7
- •650002, Г. Кемерово, Институтская, 7
Гипербола
Гиперболой
называется
геометрическое множество точек плоскости,
для которых абсолютная величина разности
расстояний до двух данных точек
![]() и
и
![]() этой плоскости, называемых фокусами,
есть величина постоянная, меньшая, чем
расстояние между фокусами.
этой плоскости, называемых фокусами,
есть величина постоянная, меньшая, чем
расстояние между фокусами.
Выведем
уравнение гиперболы. Положим
![]() .
Систему координат (рис.VIII.2)
выберем так же, как и в случае эллипса.
Тогда
.
Систему координат (рис.VIII.2)
выберем так же, как и в случае эллипса.
Тогда
![]() ,
а
,
а![]() .
Если
.
Если![]() – произвольная точка гиперболы, то
– произвольная точка гиперболы, то![]() ,a
– постоянная,
,a
– постоянная,
![]() .
Это уравнение соответствует определению
гиперболы. Преобразуя его, как и в случае
эллипса, и положив
.
Это уравнение соответствует определению
гиперболы. Преобразуя его, как и в случае
эллипса, и положив![]() ,
получимканоническое
уравнение гиперболы:
,
получимканоническое
уравнение гиперболы:
![]() .
.
Гипербола
– кривая, симметричная относительно
осей и начала координат. Прямые
![]() являются асимптотами
гиперболы, величина
являются асимптотами
гиперболы, величина
![]() называется эксцентриситетом
гиперболы,
называется эксцентриситетом
гиперболы,
![]() ,
а прямые
,
а прямые
![]() – ее директрисами.
– ее директрисами.

Рис. VIII.2
Парабола
Параболой
называется
геометрическое место точек плоскости,
равноудаленных от данной точки F
и данной прямой (рис. VIII.3).
Точка F
называется фокусом
параболы, а данная прямая – директрисой
параболы. Для получения уравнения
параболы выберем систему координат
следующим образом: ось Ox
проведем через фокус F
перпендикулярно директрисе. Начало
координат поместим в точку, равноудаленную
от фокуса и директрисы. Обозначим
расстояние между фокусом и директрисой
через p.
Величина p
называется параметром параболы. В
выбранной системе координат фокус F
имеет координаты
![]() ,
а уравнение директрисы имеет вид
,
а уравнение директрисы имеет вид![]() или
или![]() ,
по определению
,
по определению![]()
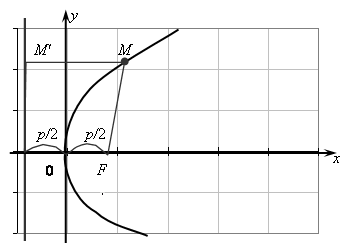
Рис. VIII.3
Пусть
![]() – произвольная точка параболы. Соединим
точкуМ
с точкой F.
Проведем отрезок MM'
перпендикулярно директрисе. Согласно
определению параболы
– произвольная точка параболы. Соединим
точкуМ
с точкой F.
Проведем отрезок MM'
перпендикулярно директрисе. Согласно
определению параболы
![]() .
По формуле расстояния между двумя
точками находим:
.
По формуле расстояния между двумя
точками находим:![]() ,
а
,
а![]() .
Следовательно,
.
Следовательно,![]() .
После элементарных преобразований
получимканоническое
уравнение параболы:
.
После элементарных преобразований
получимканоническое
уравнение параболы:
![]() .
.
Пример
VIII.3.
Классифицировать линию 2-го порядка
![]() .
.
Решение.
Воспользуемся формулой
![]() .
Выделим полный квадрат по каждой
переменной, для этого сгруппируем
отдельно слагаемые, содержащие переменнуюx
и y:
.
Выделим полный квадрат по каждой
переменной, для этого сгруппируем
отдельно слагаемые, содержащие переменнуюx
и y:
![]() .
Коэффициенты при переменных в старшей
степени вынесем общими множителями
.
Коэффициенты при переменных в старшей
степени вынесем общими множителями![]() .
Полученные выражения вскобках
дополним до полного квадрата, в первом
случае прибавим и отнимем 25, во втором
– 4:
.
Полученные выражения вскобках
дополним до полного квадрата, в первом
случае прибавим и отнимем 25, во втором
– 4:
![]() .
После раскрытия скобок постоянные
перенесем в правую часть равенства
.
После раскрытия скобок постоянные
перенесем в правую часть равенства![]() .Приведем
подобные
.Приведем
подобные
![]() .
Запишем уравнение линии 2-го порядка в
общем виде. Разделим последнее равенство
на 36, чтобы получить единицу в правой
части
.
Запишем уравнение линии 2-го порядка в
общем виде. Разделим последнее равенство
на 36, чтобы получить единицу в правой
части
![]() или
или
![]() .
.
Данная
линия (рис. VIII.4)
является гиперболой с центром в точке
![]() и полуосями
и полуосями![]() ,
,![]() .
.
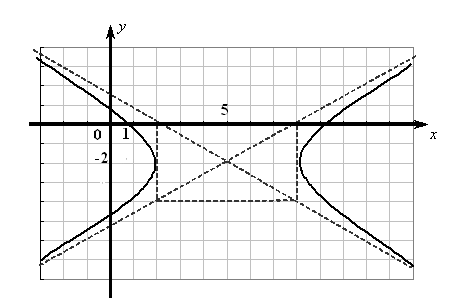
Рис. VIII.4
Классификация поверхностей второго порядка
II.
Рассмотрим в
![]() поверхность 2-го порядка, которая имеет
размерность
поверхность 2-го порядка, которая имеет
размерность![]() 9,
10.
9,
10.
Определение.
Поверхностью 2-го порядка в декартовой
системе координат
![]() пространства
пространства![]() называется множество точек, удовлетворяющих
уравнению вида
называется множество точек, удовлетворяющих
уравнению вида
![]()
![]() .
(VIII.5)
.
(VIII.5)
Линейным преобразованием (матрицей линейного оператора) уравнение (VIII.5) приводится к одному из пяти линейно независимых уравнения канонического вида
1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
(VIII.6)
,
(VIII.6)
4)
![]() ,
,
5)
![]() ,
,
где коэффициенты во всех уравнениях не равны 0.
Как и ранее, выделим классы поверхностей:
невырожденные и нераспадающиеся поверхности:
![]() эллипсоид
(рис. VIII.5);
эллипсоид
(рис. VIII.5);
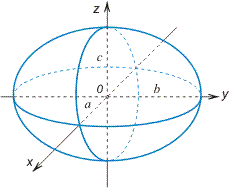
Рис. VIII.5
Если
![]() ,
то эллипсоид становится сферой
(рис.VIII.6);
,
то эллипсоид становится сферой
(рис.VIII.6);
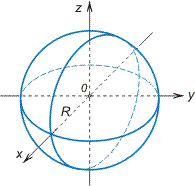
Рис. VIII.6
![]() мнимый
эллипсоид;
мнимый
эллипсоид;
![]()
однополостной
гиперболоид (рис.
VIII.7);
однополостной
гиперболоид (рис.
VIII.7);
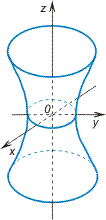
Рис. VIII.7
![]()
двуполостной
гиперболоид (рис.
VIII.8);
двуполостной
гиперболоид (рис.
VIII.8);
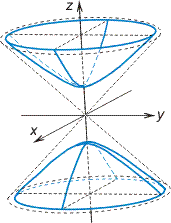
Рис. VIII.8
![]() ,
,
![]()
эллиптический
параболоид
(рис. VIII.9);
эллиптический
параболоид
(рис. VIII.9);
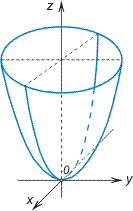
Рис. VIII.9
![]() ,
,
![]()
гиперболический
параболоид
(рис. VIII.10);
гиперболический
параболоид
(рис. VIII.10);

Рис. VIII.10
вырождающиеся нераспадающиеся поверхности:
![]() мнимый
эллиптический цилиндр;
мнимый
эллиптический цилиндр;
![]() эллиптический
цилиндр
(рис.
VIII.11);
эллиптический
цилиндр
(рис.
VIII.11);
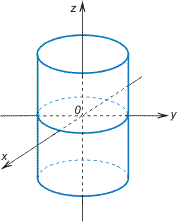
Рис. VIII.11
![]() гиперболический
цилиндр
(рис. VIII.12);
гиперболический
цилиндр
(рис. VIII.12);
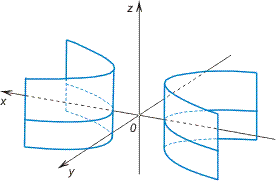
Рис. VIII.12
![]() параболический
цилиндр
(рис. VIII.13);
параболический
цилиндр
(рис. VIII.13);
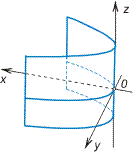
Рис. VIII.13
![]() коническая
поверхность
(рис. VIII.14);
коническая
поверхность
(рис. VIII.14);

Рис. VIII.14
![]() мнимая
коническая поверхность;
мнимая
коническая поверхность;
вырождающиеся распадающиеся поверхности:
![]() пара
мнимых пересекающихся плоскостей;
пара
мнимых пересекающихся плоскостей;
![]() пара
пересекающихся прямых;
пара
пересекающихся прямых;
![]() пара
мнимых параллельных плоскостей;
пара
мнимых параллельных плоскостей;
![]() пара
параллельных плоскостей;
пара
параллельных плоскостей;
![]() пара
совпадающих плоскостей.
пара
совпадающих плоскостей.
Пример VIII.4. Преобразовать к каноническому виду поверхность 2-го порядка
![]() .
.
Решение.
Прежде чем переходить к повороту осей
координат
![]() ,
осуществим линейный перенос так, чтобы
можно было применить методику квадратичных
форм. Положим
,
осуществим линейный перенос так, чтобы
можно было применить методику квадратичных
форм. Положим
![]() ,
,
![]() ,
,![]() ,
,
тогда поверхность запишется в виде
![]() .
.
Рассмотрим квадратичную форму
![]() .
.
Составим матрицу квадратичной формы
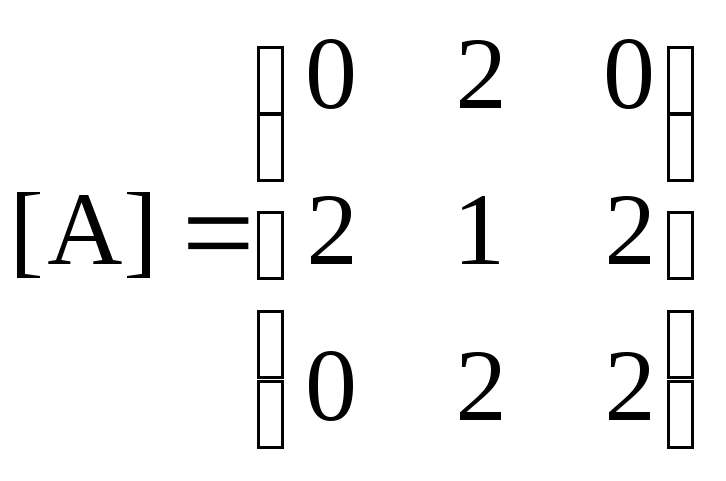 .
.
Найдем собственные числа и собственные векторы. Имеем характеристический многочлен:
![]() ,
,
корни
которого
![]() ,
,![]() ,
,![]() .
.
Запишем канонический вид поверхности с точностью до коэффициентов (сначала запишем их положительные значения):
![]() .
.
По классификации это однополостной гиперболоид. Явный вид линейного преобразования находим аналогично примерам предыдущего раздела:
 ,
,
где первое слагаемое определяет параллельный сдвиг, а второе поворот вокруг оси симметрии. Окончательно

