
- •Новокузнецк
- •Общие положения
- •1. Постановка задачи
- •2.1 Поисковые методы.
- •2.1.1 Метод сканирования.
- •2.1.2. Метод циклического координатного поиска Гаусса-Зейделя
- •2.1.2 Метод прямого поиска Хука - Дживса.
- •2.1.3. Метод Розенброка
- •2.2 Методы поиска экстремума функции, использующие расчет значений функции в вершинах многогранника.
- •2.2.1. Симплекс метод
- •2.2.2. Метод Нелдера и Мида.
- •2.3 Методы с использованием производных 1-го порядка
- •2.3.1 Градиентный метод
- •2.3.2. Метод наискорейшего спуска.
- •2.3.3 Метод крутого восхождения.
- •2.4 Методы с использованием производных 2-го порядка
- •2.4.1. Метод сопряженных направлений.
- •Алгоритмы и примеры решения задач многомерной оптимизации
2.2 Методы поиска экстремума функции, использующие расчет значений функции в вершинах многогранника.
2.2.1. Симплекс метод
Одним из эффективных методов поиска оптимума функции многих переменных является симплекс метод Симплексом в пространстве n переменных называется выпуклый многогранник, имеющий n + 1 вершину. В пространстве двух переменных – это треугольник, в пространстве трех переменных – тетраэдр. В первоначальном симплексном методе использовался правильный симплекс, т.е. симплекс, все ребра которого равны между собой (например, равносторонний треугольник).
Р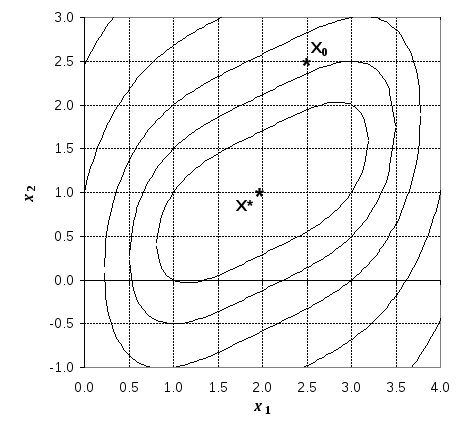









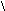
 ис.2.3
Графическая иллюстрация поиска минимума
функции методом Розенброка.
ис.2.3
Графическая иллюстрация поиска минимума
функции методом Розенброка.
Размещение правильного симплекса в пространстве n переменных может быть осуществлено различными путями. Часто используются два следующих способа.
1. Одна вершина симплекса помещается в начало координат, а остальные вершины располагаются так, чтобы ребра, выходящие из первой вершины, образовали одинаковые углы с соответствующими координатными осями. Координаты вершин симплекса в этом случае могут быть заданы следующей матрицей:
|
Номера вершин |
x1 |
x2 |
x3 |
… |
xn |
|
1 |
0 |
0 |
0 |
… |
0 |
|
2 |
P |
Q |
Q |
… |
Q |
|
3 |
Q |
P |
Q |
… |
Q |
|
… |
… |
… |
… |
… |
… |
|
n + 1 |
Q |
Q |
Q |
… |
P |
В
этой матрице P
= (1/![]() )
)![]() ;Q = (1/
;Q = (1/![]() )
)![]()
2. Центр симплекса помещается в начало координат, а (n+1) вершина на ось хn. Остальные вершины располагаются симметрично относительно координатных осей. В этом случае координаты вершин симплекса определяются матрицей:
|
Номера вершин |
x1 |
x2 |
x3 |
… |
xn |
|
1 |
-R1 |
-R2 |
-R3 |
… |
-Rn |
|
2 |
V1 |
-R2 |
-R3 |
… |
-Rn |
|
3 |
0 |
V2 |
-R3 |
… |
-Rn |
|
… |
… |
… |
… |
… |
… |
|
n + 1 |
0 |
0 |
0 |
… |
Vn |
где
Ri=1/![]() ;
Vi=1/
;
Vi=1/![]()
И в первом, и во втором случаях формулы получены для симплекса, длина ребра которого равна единице. Для произвольной длины каждую формулу надо умножить на длину ребра l.
Идея симплекс метода заключается в следующем. Выбирается начальный симплекс (А-В-С) и в его вершинах рассчитываются значения целевой функции f(A), f(В), f(C). Из этих значений находится “наихудшая” точка: при поиске минимума функции эта та точка, в которой функция принимает наибольшее значение. Например, точка А. Через центр противолежащей грани (в данном случае это сторона В-С) строится новая вершина симплекса А', симметричная А. В результате получается симплекс А-В-А', причем значения целевой функции в двух его вершинах уже известны. Поэтому вычисляется значение функции в точке А' и среди всех вершин ищется вершина с “наихудшим” значением. Эта вершина (например С) снова отображается через центр противолежащей грани (сторона В-А') и вся процедура повторяется. При приближении к области экстремума возникает ситуация, когда значения целевой функции в полученной новой вершине снова оказывается «наихудшим». В простом симплексном методе обнаружение зацикливания является признаком того, что поиск экстремума необходимо закончить. Однако в этом случае точность нахождения экстремума будет целиком определяться размером симплекса. Если исходный симплекс имеет большие размеры, то, как правило, мало вероятно, что в ходе поиска одна из вершин поиска попадет в экстремум. Если же взять исходный симплекс с малой длиной ребра, то в этом случае резко возрастает количество вычислений целевой функции. Поэтому в применяемых модификациях данного метода при обнаружении зацикливания уменьшают размеры исходного симплекса. В окрестности экстремума процедура уменьшения размеров симплекса будет многократно повторяться, и в результате симплекс будет постоянно уменьшаться, стягиваясь в точке. Как только размер симплекса станет меньше выбранной точности поиска, процесс оптимизации закончится.
Алгоритм симплекс метода.
Начальный этап. Пусть 0 - скаляр, используемый в критерии остановки, l – длина ребра симплекса, α – коэффициент уменьшения размеров симплекса. Выбрать начальную точку X1, рассчитать вершины исходного симплекса X1, X2, …, Хn+1, определить значение функции в этих вершинах f(X1),…, f(Xn+1) и перейти к основному этапу.
Основной
этап. Шаг 1.
Определить из n+1
вершин вершину с максимальным значением
функции и соответствующий ей номер j.
Рассчитать новую вершину Хn+2=![]() .
Если f(Xn+2)≤
f(Xj),
то Xj=Xn+2
и перейти к шагу 1. В противном случае
перейти к шагу 2.
.
Если f(Xn+2)≤
f(Xj),
то Xj=Xn+2
и перейти к шагу 1. В противном случае
перейти к шагу 2.
Шаг
2. Если длина ребра ![]() , то остановиться;
в противном случае провести редукцию
симплекса. Выбрать изn+1
вершин вершину с минимальным значением
функции и соответствующий ей номерm.Рассчитать вершины нового симплексаXi=((1- α )Xm
+ Xi)/α
дляi ≠m,
вычислить значения функцииf(X1),…,f(Xn+1)
и перейти к шагу 1.
, то остановиться;
в противном случае провести редукцию
симплекса. Выбрать изn+1
вершин вершину с минимальным значением
функции и соответствующий ей номерm.Рассчитать вершины нового симплексаXi=((1- α )Xm
+ Xi)/α
дляi ≠m,
вычислить значения функцииf(X1),…,f(Xn+1)
и перейти к шагу 1.
Пример расчета экстремума функции симплекс-методом.
Постановка задачи. Минимизировать f(X) = (x1 - 2)4 + (х1 - 2х2)2 с точностью =0,01. Выбираем начальное приближение X(1) = [2.5, 2.5]Т, длину ребра симплекса l=0.5 и коэффициент сжатия симплекса = 2.
Результаты расчета для данных условий представлены в таблице 2.4, графическая интерпретация метода – на рисунке 2.4.
Таблица 2.4
Результаты расчета минимума функции f(X) = (x1 - 2)4 + (х1 - 2х2)2 симплекс методом.
|
№ |
№ вершины |
x1 |
x2 |
f(X) |
№ |
№ вершины |
x1 |
x2 |
f(X) |
|
1 |
1 |
2.250 |
2.360 |
6.1048 |
8 |
1 |
2.500 |
1.520 |
0.3541 |
|
2 |
2.500 |
2.780 |
9.4261 |
2 |
2.625 |
1.310 |
0.1526 | ||
|
3 |
2.750 |
2.360 |
4.1973 |
3 |
2.750 |
1.520 |
0.4005 | ||
|
2 |
1 |
2.250 |
2.360 |
6.1048 |
9 |
1 |
2.500 |
1.520 |
0.3541 |
|
2 |
2.500 |
1.940 |
1.9669 |
2 |
2.625 |
1.310 |
0.1526 | ||
|
3 |
2.750 |
2.360 |
4.1973 |
3 |
2.375 |
1.310 |
0.0798 | ||
|
3 |
1 |
3.000 |
1.940 |
1.7744 |
10 |
1 |
2.500 |
1.100 |
0.1525 |
|
2 |
2.500 |
1.940 |
1.9669 |
2 |
2.625 |
1.310 |
0.1526 | ||
|
3 |
2.750 |
2.360 |
4.1973 |
3 |
2.375 |
1.310 |
0.0798 | ||
|
4 |
1 |
3.000 |
1.940 |
1.7744 |
11 |
1 |
2.500 |
1.100 |
0.1525 |
|
2 |
2.500 |
1.940 |
1.9669 |
2 |
2.250 |
1.100 |
0.0064 | ||
|
3 |
2.750 |
1.520 |
0.4005 |
3 |
2.375 |
1.310 |
0.0798 | ||
|
5 |
1 |
3.000 |
1.940 |
1.7744 |
12 |
1 |
2.125 |
1.310 |
0.2453 |
|
2 |
3.250 |
1.520 |
2.4855 |
2 |
2.250 |
1.100 |
0.0064 | ||
|
3 |
2.750 |
1.520 |
0.4005 |
3 |
2.375 |
1.31 |
0.0798 | ||
|
Редукция симплекса |
Редукция симплекса | ||||||||
|
6 |
1 |
2.88 |
1.730 |
0.9284 |
13 |
1 |
2.188 |
1.205 |
0.0507 |
|
2 |
2.63 |
1.730 |
0.8498 |
2 |
2.313 |
1.205 |
0.0190 | ||
|
3 |
2.75 |
1.520 |
0.4005 |
3 |
2.375 |
1.310 |
0.0798 | ||
|
7 |
1 |
2.50 |
1.520 |
0.3541 |
| ||||
|
2 |
2.63 |
1.730 |
0.8498 | ||||||
|
3 |
2.75 |
1.520 |
0.4005 | ||||||
Из таблицы видно, что на пятой итерации происходит зацикливание симплекса, так как отраженная вершина № 2 вновь становится «наихудшей». После редукции симплекса реализовано семь итераций, после чего вновь появляется эффект зацикливания. В результате чего вновь производится редукция. Полученный симплекс не находится в области экстремума функции. Поэтому проведенная редукция не дает желаемого результата, что говорит о плохой сходимости метода на функциях "овражного" типа.
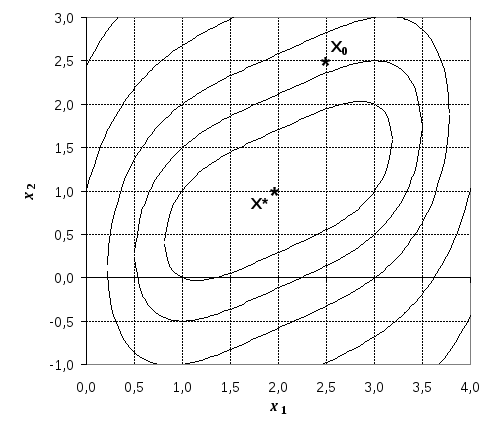

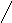












Рис.2.4.
Графическая иллюстрация поиска минимума
функции симплекс-методом.
