2.3.2. Метод наискорейшего спуска.

Отличается тем, что вдоль направления указанного градиентом из Х^(k) в Х^(k+1) осуществляется одномерный поиск, тогда вектор перехода может быть определен выражением

X^(k+1) = X^(k) + ^*(k) ^(k),

где ^*(k)- оптимальная величина шага.

В точке Х^(k+1)выбирается новое направление по градиенту и опять совершается одномерный поиск для направления^*(k). Величина^*(k)может быть определена любым методом одномерного поиска.

Алгоритм метода наискорейшего спуска.

Начальный этап. Выбрать начальную точку X⁽¹⁾, и   0 - скаляр, используемый в критерии остановки. Положить k = 1 и перейти к основному этапу.

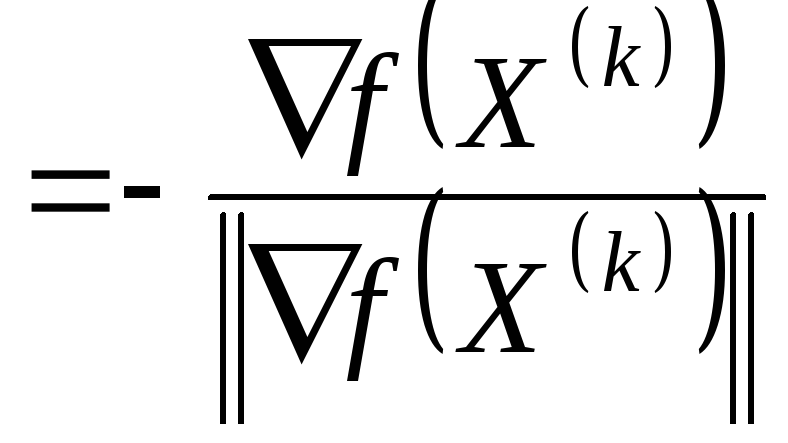Основной этап. Шаг 1. Вычислить ^(k).Любым методом одномерной оптимизации найти ^(k)* - оптимальное решение задачи минимизации функции f(Х^(k) + ^(k)^(k)) и положить X^(k+1) = X^(k) + _j^*(k).

Шаг 2. Если ||X^(k+1) - X^(k)||  , то остановиться; в противном случае заменить k на k + 1 и перейти к шагу 1.

Пример расчета экстремума функции методом наискорейшего спуска.

Постановка задачи. Найти минимум функции f(x) = (x₁ - 2)⁴ + (х₁ - 2х₂)². Выбираем начальное приближение Х⁽¹⁾ = [2.5; 2.5]^Т и точность поиска =0,01.

Результаты расчетов для данного варианта представлены в таблице 2.7, траектория поиска приведена на рис. 2.7.

Таблица 2.7.

Результаты расчета минимума функции f(x) = (x₁ - 2)⁴ + (х₁ - 2х₂)² методом крутого восхождения.

№	x1	x2	f(Х)				Δx1	Δx2	λ	Критерий
1	2.500	2.500	6.31250	-4.50000	10.00000	10.96586	0.410	-0.912		не достигнут
2	2.909	1.592	0.75738	2.44911	1.10210	2.68566	-0.912	-0.410	0.996	не достигнут
3	2.257	1.299	0.12043	-0.61318	1.36262	1.49422	0.410	-0.912	0.714	не достигнут
4	2.318	1.165	0.01033	0.10471	0.04712	0.11482	-0.912	-0.410	0.147	не достигнут
5	2.117	1.074	0.00120	-0.05736	0.12747	0.13979	0.410	-0.912	0.220	не достигнут
6	2.123	1.062	0.00023	0.00601	0.00270	0.00659	-0.912	-0.410	0.014	не достигнут
7	2.068	1.037	0.00006	-0.01111	0.02468	0.02707	0.410	-0.912	0.060	не достигнут
8	2.069	1.034	0.00002	0.00106	0.00048	0.00116	-0.912	-0.411	0.003	достигнут

На 8-ой итерации достигнута заданная точность и найдена оптимальная точка Х*=[2.069; 1.034]^т.

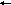
Рис.2.7 Графическая иллюстрация поиска минимума функции методом наискорейшего спуска.

2.3.3 Метод крутого восхождения.

Этот метод называют еще методом Бокса и Уилсона. Этот метод представляет пошаговую процедуру по поверхности отклика, в которой для оценки составляющих градиента f(X^(k)) = [b₁^(k), b₂^(k), …, b_n^(k)] используется линейное уравнение регрессии в кодированных переменных f(X^(k)) = b₀^(k) + b₁^(k)x₁^(k) + b₂^(k)x₂^(k) + … + b_n^(k)x_n^(k), полученное в результате планирования эксперимента в окрестности точки Х^(k). Затем совершается движение (крутое восхождение) по направлению f(X^(k)), которое определяется произведением коэффициента b_j^(k) на интервал варьирования переменных х_j^(k) при планировании эксперимента в окресности X^(k). Это движение можно рассматривать как этап, аналогичный методу наискорейшего спуска, в котором решается задача одномерного поиска. В полученной точке Х^(k+1) снова производится планирование эксперимента и выбор нового направления движения.

Необходимо отметить, что данный метод по принципу используемой информации (только значение функции) можно отнести к поисковым методам, а по способу движения - к градиентным. Кроме того, появляется возможность свертки информации о поверхности отклика в виде совокупности линейных уравнений регрессии. Отмеченные особенности характеризуют положительные достоинства этого метода.

Алгоритм метода крутого восхождения.

Начальный этап. Выбрать начальную точку X₀⁽¹⁾=[]^T, интервал варьирования X⁽¹)=[x₁⁽¹⁾,  x₂⁽¹⁾,…, x_n⁽¹⁾]^T и   0 - скаляр, используемый в критерии остановки, - коэффициент сжатия шага, n–размерность задачи, число опытов равно N=2ⁿ. Положить k=1, i=1 и перейти к основному этапу.

Основной этап. Шаг 1. Вычислить натуральное и кодированное значение переменной х^(k)_i=x_i^(k) и Y_i=(x_i^(k)-x_0i^(k))/x_i^(k). Если i=n, то положить j=1 и перейти к шагу 2, иначе положить i=i+1 и вернуться к шагу 1.

Шаг 2. В соответствии с матрицей планирования полного факторного эксперимента реализовать полный факторный эксперимент в окресности точки X^(k). Определить значение функции f(Х_j^(k)). Если j=N, то положить i=1, j=1 и перейти к шагу 3, иначе вернуться к шагу 2.

Шаг 3. Вычислить коэффициенты аппроксимационного уравнения f(X^(k)) = b₀^(k) + b₁^(k)x₁^(k) + b₂^(k)x₂^(k) + … + b_n^(k)x_n^(k) по формуле 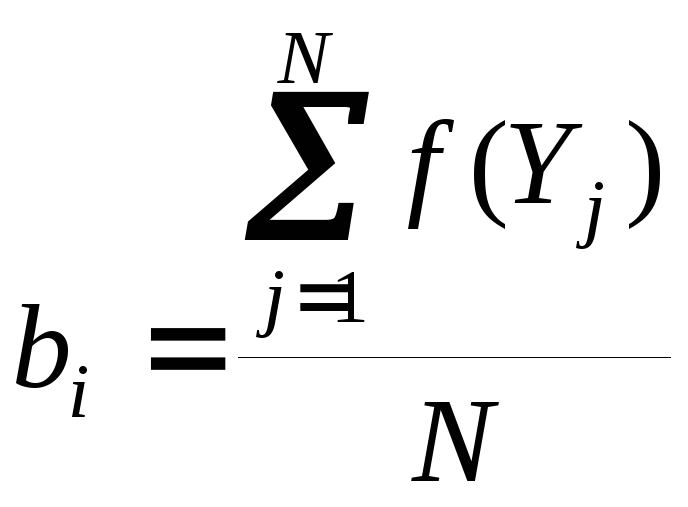. Еслиi=n, то перейти к шагу 4, иначе вернуться к шагу 3.

Шаг 4. Определить значение функции в точке (X^(k)- jX^(k)B), если f(X^(k)- jX^(k)B)<f(X^(k)), то положить j=j+1 и вернуться к шагу 4, иначе X^(k+1)= (X^(k)- jX^(k)B), k=k+1 и перейти к шагу 5.

Шаг 5. Если ||X^(k+1) - X^(k)||  , то остановиться; в противном случае i=j=1и перейти к шагу 1.

Пример расчета экстремума функции методом крутого восхождения.

Постановка задачи. Найти минимум функции f(x) = (x₁ - 2)⁴ + (х₁ - 2х₂)². Выбираем начальное приближение Х⁽¹⁾ = [2.5; 2.5]^Т, интервал варьирования на первой итерации принимаем X⁽¹)=[0.5; 0.5]^T, ⁽¹⁾=0,05 и точность поиска =0,01.

Результаты расчетов минимума функции методом крутого восхождения с использованием табличного процессора EXCEL для данного варианта представлены в таблице 2.8. Траектория поиска метода приведена на рис.2.8.

Таблица 2.8.

Результаты расчета минимума функции f(x) = (x₁ - 2)⁴ + (х₁ - 2х₂)² методом крутого восхождения.

1. Эксперимент в точке [2.5,2.5], Δx1=0.5, Δx2=0.5,
№		Y1		Y2		x1		x2		f(X)		b1		b2
1		-1		-1		2.00		2.00		4.00		-2.00		5.00
2		1		-1		3.00		2.00		2.00		=0.05
3		-1		1		2.00		3.00		16.00
4		1		1		3.00		3.00		10.00
Движение в направлении градиента
№		x1		x2		f(X)		№		x1		x2		f(X)
1		2.500		2.500		6.3125		4		2.800		1.750		0.8996
2		2.600		2.250		3.7396		5		2.900		1.500		0.6661
3		2.700		2.000		1.9301		6		3.000		1.250		1.2500
2. Эксперимент в точке [2.9,1.5], Δx1=0.5, Δx2=0.5,
№	Y1		Y2		x1		x2		f(X)		b1		b2
1	-1		-1		2.40		1.00		0.1856		1.81		0.20
2	1		-1		3.40		1.00		5.8016		=0.1
3	-1		1		2.40		2.00		2.5856
4	1		1		3.40		2.00		4.2016
Движение в направлении градиента
№	x1		x2		f(X)		№		x1		x2		f(X)
1	2.900		1.500		0.6661		3		2.538		1.460		0.2296
2	2.719		1.480		0.3255		4		2.358		1.440		0.2893
2. Эксперимент в точке [2.538,1.460], Δx1=0.75, Δx2=0.5,
№	Y1		Y2		x1		x2		f(X)		b1		b2
1	-1		-1		1.788		0.960		0.0193		0.80		0.76
2	1		-1		3.288		0.960		4.6280		=0.1
3	-1		1		1.788		1.960		4.5457
4	1		1		3.288		1.960		3.1544
Движение в направлении градиента
№	x1		x2		f(X)		№		x1		x2		f(X)
1	2.538		1.460		0.2296		5		2.217		1.155		0.0108
2	2.458		1.384		0.1397		6		2.136		1.078		0.0008
3	2.378		1.307		0.0766		7		2.056		1.002		0.0027
4	2.297		1.231		0.0350		Критерий						Достигнут

Врезультате трех итераций реализации метода крутого восхождения получена точкаХ*=[2.056; 1,002]^т, значение функции в которой f(Х*)=0.0027.

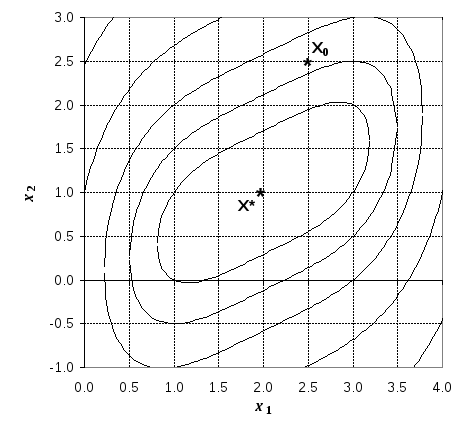Рис.2.8 Траектория поиска минимума функции методом крутого восхождения.