2.2.2. Метод Нелдера и Мида.

Отмеченные выше недостатки регулярного симплекса, а также отсутствие ускорения поиска и трудности при проведении поиска на искривленных “оврагах” и “хребтах” явились причиной разработки Нелдером и Мидом метода, в котором симплекс меняет свою форму, т. е. представляет деформируемый многогранник. Изменение формы многогранника происходит за счет операций растяжения, сжатия и редукции.

1. Построение начального многогранника. Выбирается произвольной формы многогранник с координатами вершин

X_i^(k) = [x_i1^(k), …, x_ij^(k), …, x_in^(k)]^Т, i = 1, …, n+1.

Индекс (k) будет обозначать k-й этап поиска. Значение целевой функции в X_i^(k) равно f(X_i^(k)).

2. Расчет координат центра тяжести. Определяют те векторы х многогранника, которые дают максимальное и минимальное значение f(X), а именно

f(X_h^(k)) = maxf(X₁^(k)), …, f(X_n+1^(k));f(X_l^(k)) = min f(X₁^(k)), …, f(X_n+1^(k)).

Тогда координаты центра тяжести рассчитываются по формуле

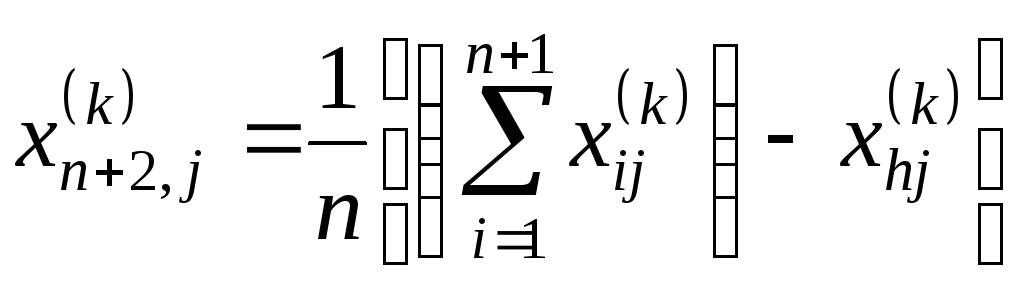, j = 1, …, n,

где индекс jобозначает координатное направление.

3. Отражение. Представляет проектирование X_h^(k) через центр тяжести в соответствии с соотношением

,

где   0 - коэффициент отражения;

X_h^(k)- вершина, в которой функцияf(X) имеет наибольшее значение.

В обычном симплексе  = 1.

4. Растяжение. Происходит в случае, если . Вектор () увеличивается в соответствии с соотношением

,

где   1 - коэффициент растяжения.

Если , то заменяется на и процедура продолжается с этапа 2 при k = k + 1. Иначе заменяется на и также осуществляется переход к этапу 2 при k = k + 1.

5. Сжатие. Если для всех i  h, то вектор () уменьшается в соответствии с формулой

,

где 0    1 - коэффициентом сжатия.

Затем заменить на и происходит возврат к операции 2 приk = k + 1.

6. Редукция. Происходит при условии, если . Все векторы () уменьшаются в 2 раза с отсчетом от в соответствии с формулой

, i=1, …, n+1.

Затем возвращаемся к операции 2 для продолжения поиска на (k+1)-м шаге.

Для окончания поиска Нилдер и Мид используют критерий вида

 ,

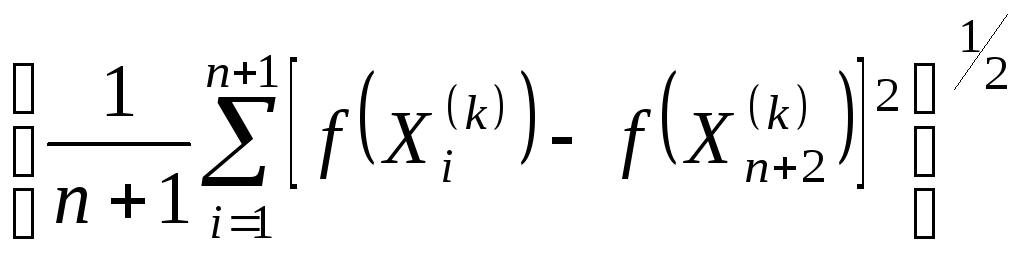
где  - заданная точность поиска;

- значение функции в центре тяжести.

Пример расчета минимума функции методом деформируемого многогранника.

Постановка задачи. Рассматриваем задачу минимизации функции f(X)=(x₁-2)⁴+ (х₁ - 2х₂)².

Вершины начального многогранника рассчитываем как в обычном симплексе

X₁⁽¹⁾ = [2.25 2.36]^Т; X₂⁽¹⁾ = [2.5 2.78]^Т; X₃⁽¹⁾ = [2.75 2.36]^Т.

Зададим параметры алгоритма  = 1;  = 0,5;  = 2.

На первой итерации при k = 1. Вычислим значение функции в вершинах исходного многогранника

f(X₁⁽¹⁾) = 6.10480; f(X₂⁽¹⁾) = 9.4261; f(X₃⁽¹⁾) = 4.197.

Наихудшей вершиной является X_h⁽¹⁾ = X₂⁽¹⁾, а наилучшей X_l⁽¹⁾ = X₃⁽¹⁾.

Определяем центр тяжести

[(2.25+ 2.50 + 2.75) – 2.5]/2 = 2.5,

[(2.36 + 2.78 + 2.36) – 2.78]/2 = 2.36.

и рассчитываем координату отражения

= 2.5 + 1(2.5 – 2.5) = 2.5,

= 2.5 + 1(2.5 – 2.78) = 1.94.

Значение функции в этой точке f(X₅⁽¹⁾) = 1.967, что меньше, чем в X₁⁽¹⁾. Поэтому, проводим операцию растяжения

= 2.5 + 2(2.5 – 2.5) = 2,5,

= 2.5 + 2(2.22 – 2.5) = 1.52.

Значение функции f(2.5 1.52) = 0.354. Поскольку f(X₆⁽¹⁾)  f(X₅⁽¹⁾), заменяем X₂⁽¹⁾ на X₆⁽¹⁾ и полагаем X₆⁽¹⁾ = X₁⁽²⁾ на следующем этапе поиска. Результаты расчета нескольких итераций метода представлены в таблице 2.5. Траектория поиска метода представлена на рис.2.5.

Таблица 2.5

Результаты расчета минимума функции f(X) = (x₁ - 2)⁴ + (х₁ - 2х₂)².

методом Нелдера-Мида.

№	Операция	x1	x2	f(X)	№	Операция	x1	x2	f(X)	№	Операция	x1	x2	f(X)
1	вершина 1	2.25	2.36	6.105	3	вершина 1	2.81	1.73	0.855	5	вершина 1	2.30	1.05	0.049
	вершина 2	2.50	2.78	9.426		вершина 2	2.75	2.36	4.197		вершина 2	2.50	1.52	0.354
	вершина 3	2.75	2.36	4.197		вершина 3	2.50	1.52	0.354		вершина 3	2.61	1.26	0.147
	ц. тяжести	2.50	2.36	4.991		ц. тяжести	2.66	1.63	0.538		ц. тяжести	2.45	1.15	0.064
	отражение	2.50	1.94	1.967		отражение	2.56	0.89	0.712		отражение	2.41	0.79	0.727
	растяжение	2.50	1.52	0.354		сжатие	2.61	1.26	0.147		редукция
2	вершина 1	2.25	2.36	6.105	4	вершина 1	2.81	1.73	0.855
	вершина 2	2.75	2.36	4.197		вершина 2	2.50	1.52	0.354
	вершина 3	2.50	1.52	0.354		вершина 3	2.61	1.26	0.147
	ц. тяжести	2.63	1.94	1.728		ц. тяжести	2.55	1.39	0.144
	отражение	3.00	1.52	1.002		отражение	2.30	1.05	0.049
	сжатие	2.81	1.73	0.855		растяжение	2.04	0.71	0.393

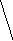
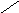
Н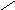а пятой итерации симплекс достиг области экстремума, что говорит о высокой эффективности метода. Отраженная вершина вновь становится «наихудшей», поэтому для достижения необходимой точности необходимо провести редукцию.

Рис.2.5 Графическая иллюстрация поиска минимума функции методом Нелдера-Мида.